基于BP神经网络的涉氨制冷企业风险分级模型

2019-11-27李春花李晓泉李昂昂何娟霞

广西大学学报（自然科学版） 2019年5期

李春花,李晓泉,李昂昂,何娟霞*,2

(1.广西大学资源环境与材料学院, 广西南宁 530004；2.华南理工大学材料科学与工程学院, 广东广州 510641)

0 引言

涉氨制冷企业属于易发生重特大事故的重点行业领域，事故主要体现为氨泄漏、火灾、爆炸等[1]。据统计数据显示，2007年至2015年这9年间，我国涉氨制冷企业仅氨泄漏事故就发生了187起，造成174人死亡、1 686人中毒，疏散近万人，并且氨泄漏事故在2012年以后呈逐年增长态势[2]。涉氨制冷企业频发的事故造成严重人员伤亡、财产损失及环境污染，带来了较坏的社会影响。究其根本原因在于企业对于风险的认识不足，掌控不足。因此，建立健全快捷方便的涉氨制冷企业风险分级评估体系，实现风险快速分级及动态监管，是目前亟需解决的问题。

现行《危险化学品重大危险源辨识》(GB 18218—2018)[3]规定，氨的临界量为10吨，单元内存在的危险化学品数量等于或超过规定的临界量即为重大危险源。针对重大危险源分级，有学者已进行过相关探讨。高进东等[4]通过对比国外标准、分析国内情况，提出我国重大危险源辨识最小标准的建议；魏利军等[5]提出了一种采用单元内各种危险化学品的总量与其临界量比值经校正系数校正后的值作为分级指标的危险化学品重大危险源分级方法；王爽等[6]在针对重大危险源临界量设置问题上，采用数值模拟和火灾爆炸事故破坏范围中的损失半径等方法，提出了多种分级方法结合的组合式分级法。在《氨制冷企业安全规范》(AQ 7015—2018)[7]公布实施之前，由于涉氨制冷行业不属于化工生产，因此在管理中未按照重大危险源的规定严格执行。目前，我国涉氨制冷企业风险研究多集中在泄漏、扩散模型上。饶国宁等[8]通过对液氨泄漏的定量分析得出风速对其扩散范围的影响；丁晓晔等[9]通过数值模拟对液氨储罐泄漏和扩散规律进行分析，运用所构建模型确定了液氨泄漏扩散趋势和范围；罗艾民等[10]对泄漏、扩散、点火在泄漏源附近一定范围内按不同时序演变的5种事故后果模式进行了对比研究，得出了每种事故的危害范围和程度；JI Jie等[11]通过对液氨储罐泄漏和扩散进行模拟，得出氨扩散距离、危险区域与风速、地面粗糙度及液氨泄漏速率之间的关系。但鲜有学者对涉氨制冷企业风险分级进行研究。

基于此，为缓和涉氨制冷企业风险分级状态，笔者依据事故致因理论与“人、物、管、环”四要素系统，从涉氨制冷企业固有风险、人员风险、环境风险及企业管理风险出发，根据涉氨制冷行业相关法律、法规、规范、标准及其他要求，通过SPSS和专家评审确定了27个涉氨制冷企业风险分级指标。基于专家打分法将南宁市11家涉氨制冷企业风险量化，量化结果作为BP神经网络模型训练的输入值；选取10组数据作为训练样本，1组作为验证样本。经验证，建立的BP神经网络模型对涉氨制冷企业风险分级具有一定程度的可靠性，有助于同类型企业及相关政府部门在进行风险分级时抓住重点，提前预防，实现风险动态管理。

1 BP神经网络运算基本原理

1986年Rumelhart和McCelland为首的科研小组提出了原始的BP神经网络[12]，其作为目前应用最为广泛的网络模型之一，具有神经网络的普遍优点。BP神经网络是一种“通过误差逆传播算法训练”的多层前馈网络[13]。在正向传播时，输入样本从输入层传入隐层，经过处理后传至输出层，在此过程中若发生实际输出与期望输出不符，则转入误差的反向传播阶段；反向传播时，将输出信号以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有神经元，从而获得各层神经元的误差信号，再以此误差信号作为修正各个神经元权重的依据。显然其传播对象是“误差”，目的是得到所有层的估计误差，通过不断调整网络权值和阈值使得全局误差系数最小，以此达到对各神经元权值的动态调整。典型的BP神经网络模型如图1所示。

BP神经网络数学原理拓扑结构如图2所示，含3个神经元的输入层、3个神经元的隐含层和3个神经元的输出层共3层的模型，其多层多维模型的数学原理同理。

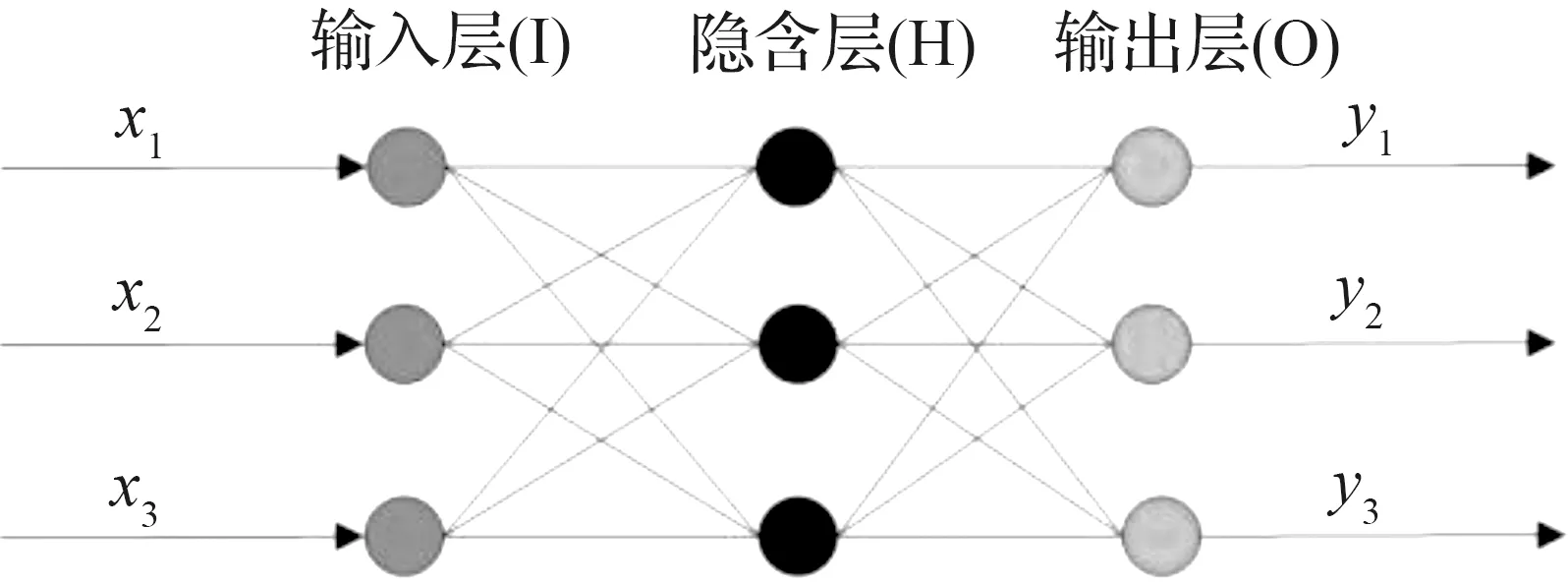
图1 BP神经网络模型

Fig.1 BP neural network model

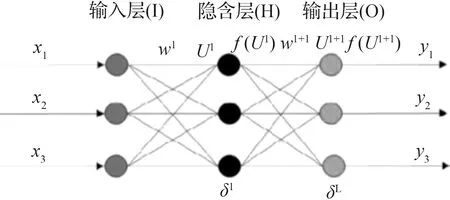
图2 BP神经网络数学原理拓扑结构

Fig.2 Topology of mathematical principle of BP neural network

其数学原理如下：

输入层向隐含层单条线路输入模型为：

h11=w11x1+b1。

(1)

因此隐含层单个神经元输入模型为：

(2)

隐含层向输出层输出模型为：

hoj=f(hij)i=1,2,3j=1,2,3。

(3)

输出层输出模型为：

(4)

输出层输出后将按照算法与期望输出d进行比较，其总误差为：

(5)

当其误差满足要求时停止计算，否则将进行误差反传，在这期间用梯度下降法对各神经元的权值w和阈值b进行调整更新直至满足要求为止，其相应的修正量Δw和Δb如下：

(6)

(7)

上式中：hi为隐含层输入值；ho为隐含层输出值；y为输出层输出值；f(·)为激活函数；g(·)为线性函数；η为步长或学习率；δ为局部梯度或灵敏度。

2 涉氨制冷企业风险分级模型构建与结果分析

2.1 涉氨制冷企业风险分级模型构建

2.1.1 指标体系确定

风险分级指标体系是风险分级的关键和基础，其对分级结果是否符合实际情况影响巨大，因而涉氨制冷企业风险分级指标要尽可能全面反映该类企业的主要特征和基本状况。

据此，本文在实地调研，查阅相关法律法规规范标准及其他要求，研究大量相关文献资料以及咨询政府职能部门、安全生产专家等工作之后，综合考虑影响企业日常安全生产活动的关键风险因素，遵循科学性、系统性、简要性、准确性、可行性等原则，从众多风险指标中筛选出36个分级指标，而后运用SPSS统计软件对所选36个指标进行降维，将其中的线性指标再次剔除，尽量剩下彼此不相关且比原始变量具有某些更优越性质的指标，经专家评审后作为此次模型建立的指标集。最后建立出涉氨制冷企业风险分级指标体系见表1所示。

表1 涉氨制冷企业风险分级指标体系

2.1.2 评价集确定

风险评价结果按照程序运行行为将其划分为5个等级，分别是：高风险(Ⅴ，80～100)、较高风险(Ⅳ，60～80)、一般风险(Ⅲ，40～60)、较低风险(Ⅱ，20～40)、低风险(Ⅰ，0～20)。

为减弱定性指标的主观性，将其按照风险评价结果用模糊语言量化[14]。具体如表2所示。

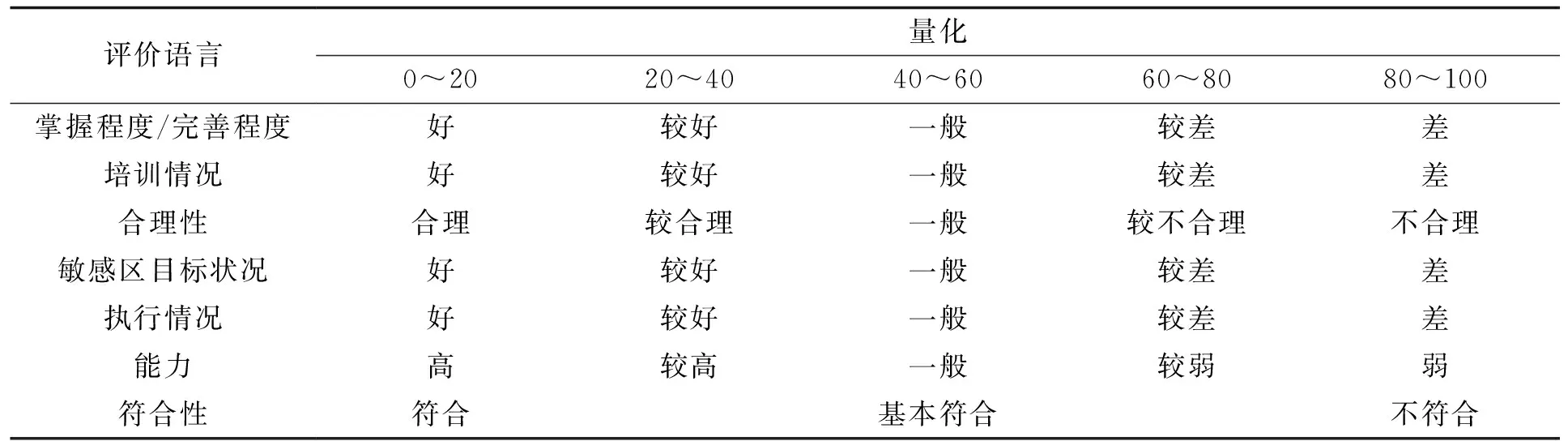
表2 定性指标模糊处理

将量化后的指标及五位专家对企业整体风险打分的平均值作为企业最后风险得分整理成表3。因为现在MATLAB新版本中不需要对数据进行归一化就可运算，所以本文直接运用表3进行样本训练和测试。

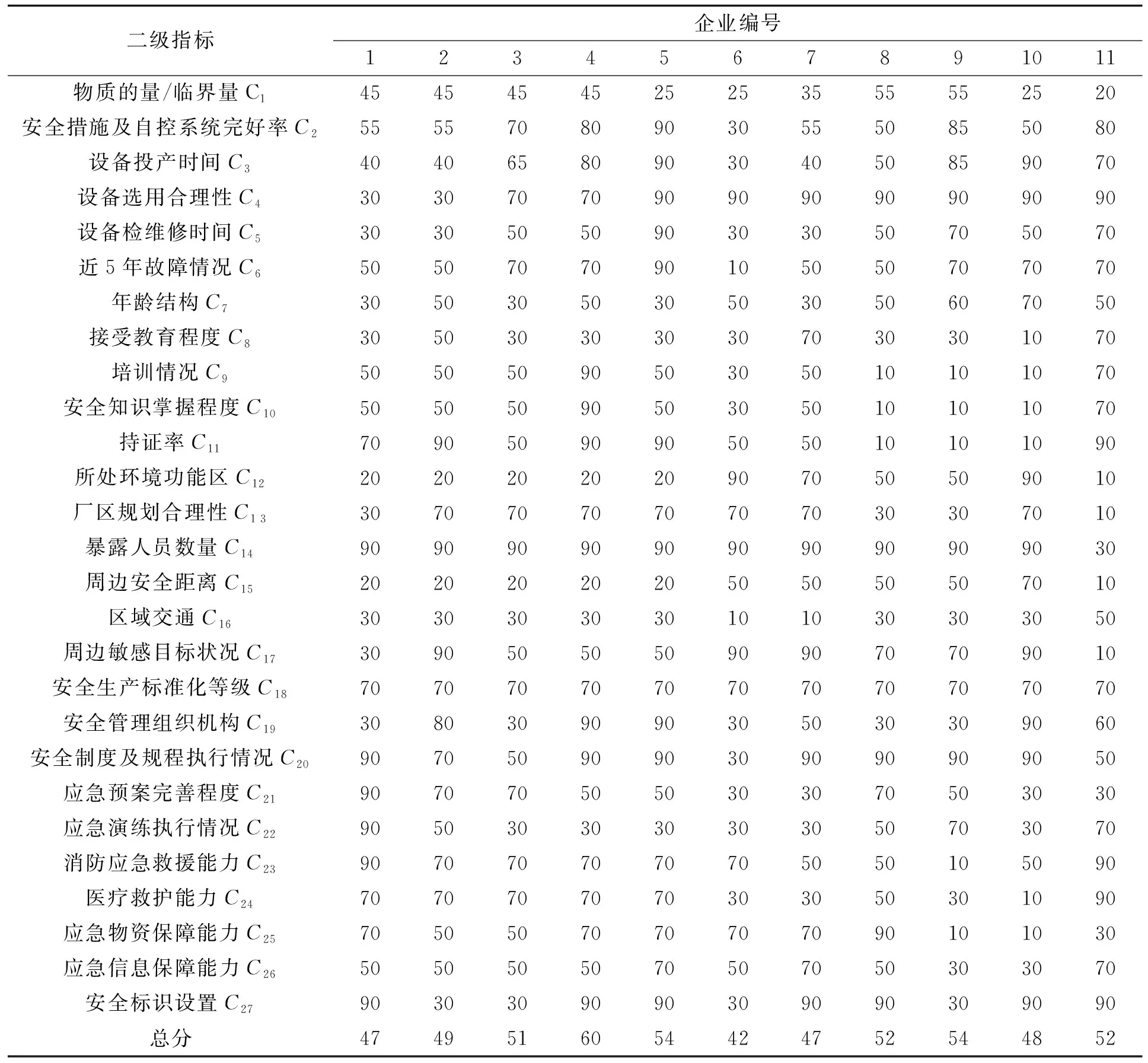
表3 量化后的风险分级指标

① 输入层n：本文有27个二级指标，故输入层神经元个数为27个。

② 输出层y：表示危险化学品重大危险源企业风险等级，输出值为0～100的常数，输出层神经元的个数为1。

③ 隐含层h：BP网络具有很强的非线性映射能力，根据Kolmogorov定理[15]，一个3层BP神经网络能够实现对任意非线性函数进行逼近，因此隐含层数选择为1层[16]。同时，隐层神经元数目对预测精度的影响至关重要，过多会过度拟合，过少会影响性能，达不到预期效果[17]。网络中的隐含层神经元数目与实际问题的复杂程度、输入和输出层的神经元数以及对期望误差的设定有着直接联系。本文参照了以下经验公式[18]和Kolmogorov定理。

④ 权值和阈值初始值：(0，1)之间的随机数。

⑤ 学习率η=0.01，按照数据在运行中被归一化后取最小绝对值也大于0.1，因此取小一个数量级的0.01比较合理，学习率取过大收敛速度快，但是在临近最佳点时会产生动荡致使无法收敛。

2.2 模型实现与验证

2.2.1 样本企业介绍

本文以广西壮族自治区南宁市内11家涉氨制冷企业中10家风险评估数据作为训练样本，另外1家企业风险评估数据作为验证样本。11家企业中，啤酒厂3家(3级重大危险源2家、4级重大危险源1家)、冷鲜肉加工2家(3级重大危险源1家、4级重大危险源1家)、冷冻饮品企业2家(3级重大危险源1家、4级重大危险源1家)、水果生鲜企业4家(3级重大危险源1家、4级重大危险源3家)。

仿真1中只分析了一种布站方式下算法对远近目标的定位，接下来给出另一种布站方式下算法的定位性能，并分析布站数量对目标定位精度的影响.定位场景如图4所示：利用接收站Rx1、Rx2和外辐射源Tx1、Tx2、Tx3，对位于[5,5]Tkm处的目标进行定位.仿真结果如图5所示.

2.2.2 模型实现与验证

将表3中前10家企业风险分级指标的各项数据输入以MATLAB(2016a)为基础的BP神经网络模型中，以隐含层节点数14为例，涉氨制冷企业的BP神经网络风险评价模型结构如图3所示。

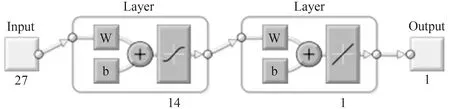
图3 隐含层节点数为14的BP神经网络模型结构图

首先确定训练数据和测试数据，即将输入的10家企业数据进行分组，本文采取随机分组模式，将10组数据中的70 %作为训练数据，15 %作为测试数据，15 %作为验证数据。

模型中的传输函数分别为tansig函数和purelin函数，训练函数采用麦夸特算法trainlm。训练次数设置为5 000次，目标误差为10-7。经训练后将数据代入进行仿真，得出最后结果。

当节点数为6时，经过4次迭代训练后模拟结果为50.666 7，拟合优度R=0.073 538，均方误差MSE=35.222 2，明显不符合要求。其拟合优度和均方误差如图4、图5。

当节点数为10时，经过6次迭代训练后模拟结果为50.400 0，拟合优度R=0.799 46，均方误差MSE=5.533 3，不符合拟合要求。其拟合优度和均方误差如图6、图7。

当节点数为14时，经过23次迭代训练后模拟结果为52.500 0，拟合优度R=0.972 46，均方误差MSE=0.75，本次结果的拟合度达到要求，但其MSE未达到要求。其拟合优度和均方误差如图8、图9。

当节点数为20时，经过17次迭代训练后模拟结果为50.000 0，拟合优度R=0.4733 5，均方误差MSE=14.333 3，不符合要求。其拟合优度和均方误差如图10、图11。

当节点数为30时，经过40次迭代训练后模拟结果为52.583 9，拟合优度R=1，均方误差MSE=3.1614e-21，拟合度和精度均达到要求，且与实际情况吻合良好，提取并保存其权值和阈值。其拟合优度及均方误差如图12、图13。

当节点数为55时，通过迭代训练47次后模拟结果为53.9470，拟合优度R=1和均方误差MSE=5.615e-20均达到要求，但训练时间较长且训练结果与实际情况的误差比隐含层为30时偏大，因此不选择隐含层数55。其拟合优度和均方误差如图14、图15。

经以上测试，建立的BP神经网络隐含层神经元节点数取30。

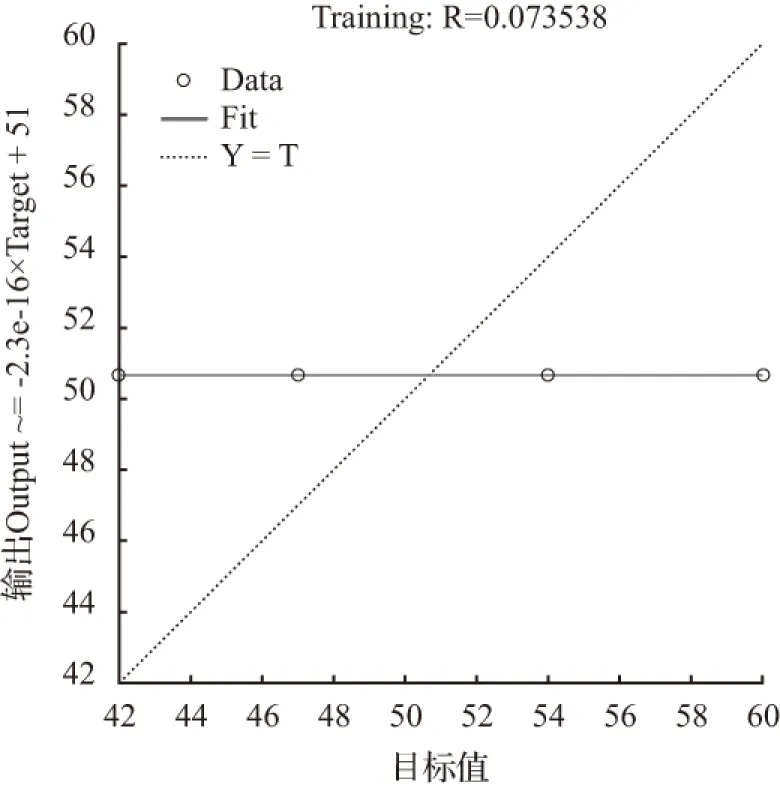
图4 拟合优度(R=0.073 538)

Fig.4 Goodness of fit (R=0.073 538)

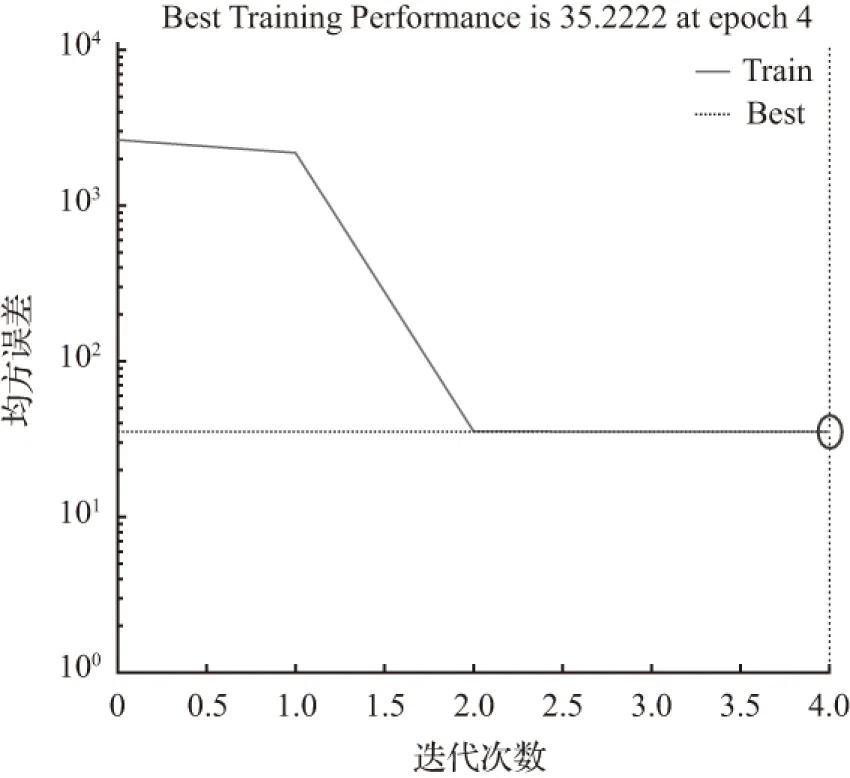
图5 均方误差(MSE=35.222 2)

Fig.5 Mean square error (MSE=35.222 2)

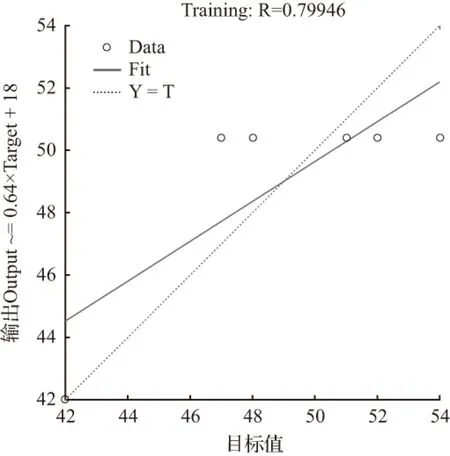
图6 拟合优度(R=0.799 46)

Fig.6 Goodness of fit (R=0.799 46)

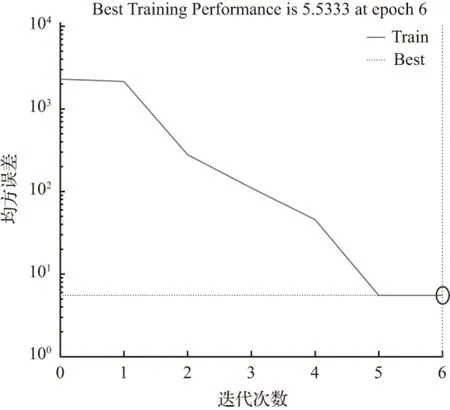
图7 均方误差(MSE=5.533 3)

Fig.7 Mean square error (MSE=5.533 3)

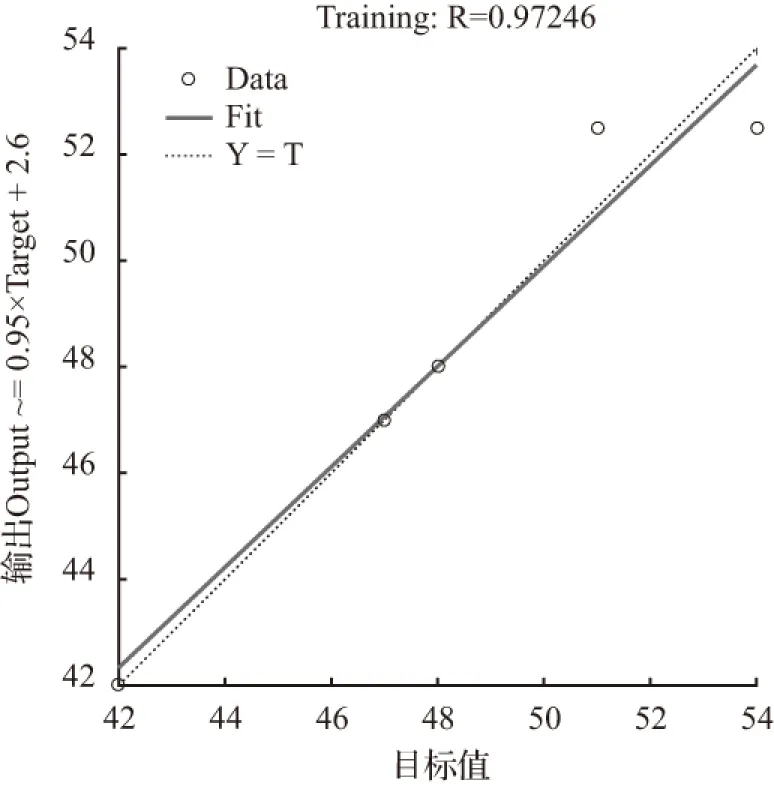
图8 拟合优度(R=0.972 46)

Fig.8 Goodness of fit (R=0.972 46)

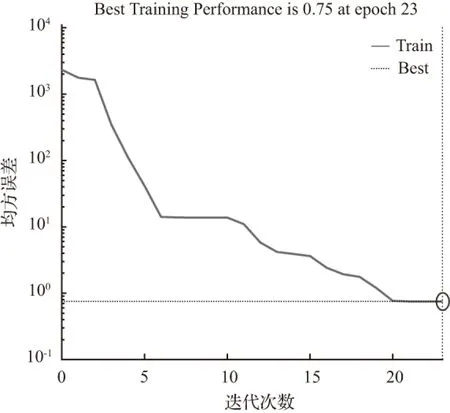
图9 均方误差(MSE=0.75)

Fig.9 Mean square error (MSE=0.75)

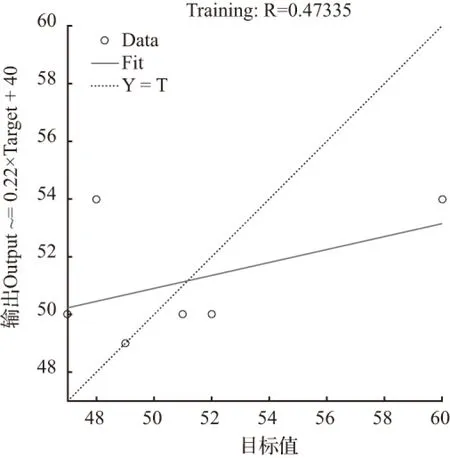
图10 拟合优度(R=0.473 35)

Fig.10 Goodness of fit (R=0.473 35)

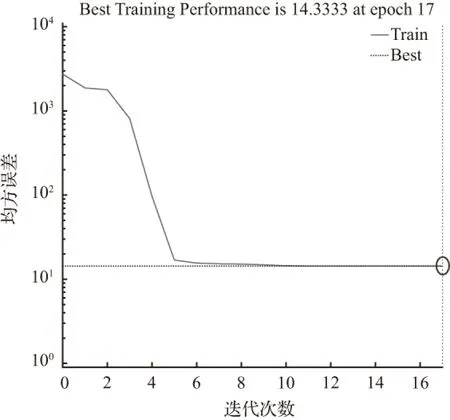
图11 均方误差(MSE=14.333 3)

Fig.11 Mean square error (MSE=14.333 3)

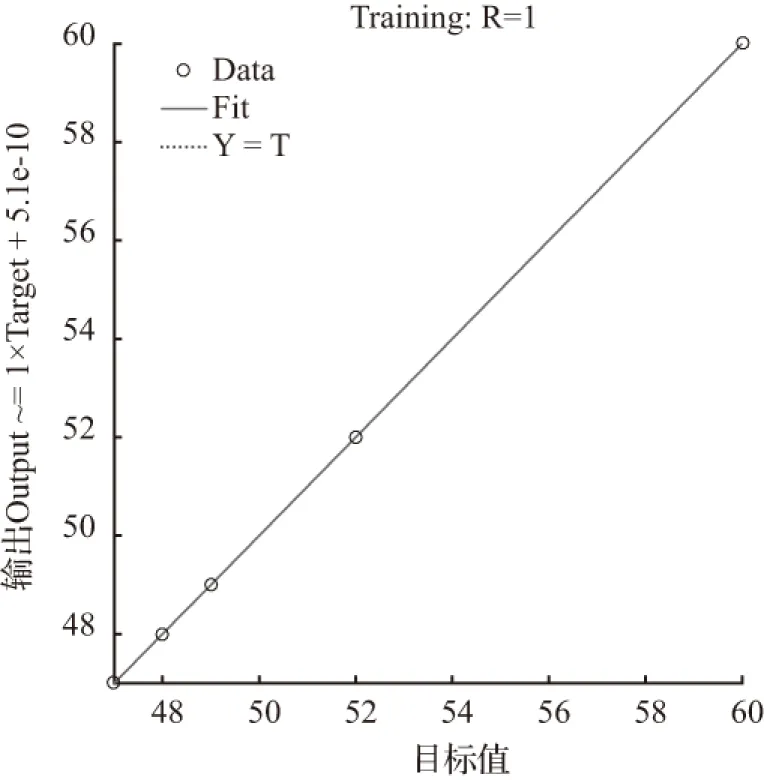
图12 拟合优度(R=1)

Fig.12 Goodness of fit (R=1)

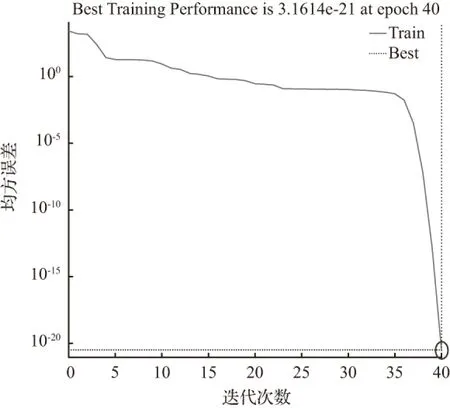
图13 均方误差(MSE=3.1614e-21)

Fig.13 Mean square error (MSE=3.1614e-21)

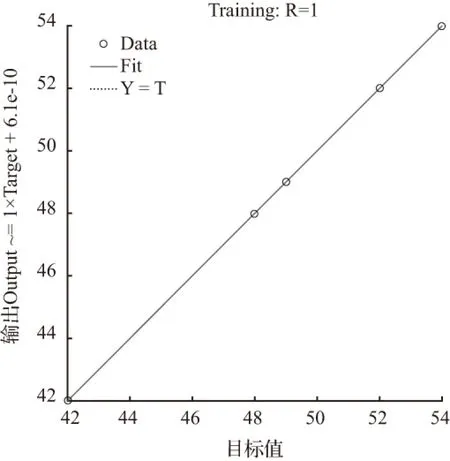
图14 拟合优度(R=1)

Fig.14 Goodness of fit (R=1)

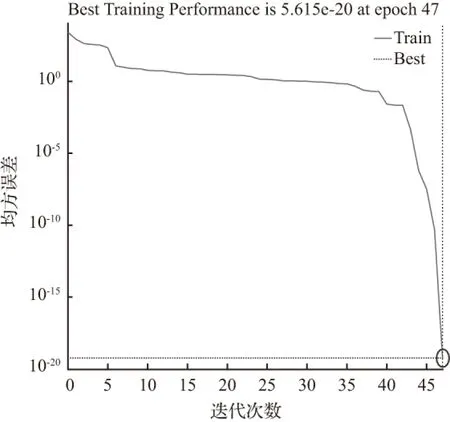
图15 均方误差(MSE=5.615e-20)

Fig.15 Mean square error (MSE=5.615e-20)

2.3 BP神经网络模型模拟结果分析

① 通过对隐含层神经元节点数的选择测试，验证了神经元节点数对模拟结果的影响十分显著。同时，常用的经验公式在面对该行业的类似数据时，效果差强人意；利用两种方法综合确定神经元节点数的大致范围，然后再逐步测试的过程虽然略显繁琐，但其能在该行业的类似数据的模拟预测中达到很好的效果。

② 在选择隐含层神经元节点数时，要注意对每次结果进行保存。BP神经网络不具备记忆性，且在模拟中一开始给定的权值和阈值是0和1之间的随机数，若不对测试时的数据进行保存，将难以再次实现该预测结果。因此建议保存每次测试结果，找到最优节点数后，将该次测试结果的权值和阈值进行提取，然后将最终模型的权值和阈值直接设定为前面的提取值。

③ 经对模拟结果分析，涉氨制冷企业与其他危险化学品企业有着显著的不同：涉氨制冷企业没有显著的风险高发点，即单独提高或者降低某项指标对企业整体风险评级影响不大，不同于其他化工企业事故发生原因多是因为设备故障，涉氨制冷企业事故原因几乎涵盖四大类指标。由此说明，该类企业风险具有分散性，致使事故的发生难以预测和预防。