关于圆锥曲线的定值问题探究

何正文

(广东省肇庆市百花中学 526000)

本文通过圆锥曲线定值定量问题的探究，帮助学生遇到圆锥曲线问题能迅速归类，举一反三，化繁为简、化难为易，达到事半功倍的效果.把握好其中不变规律，解决问题中不同的应用环境，提高学生思维品质.

一、圆锥曲线关于数轴对称点的定值问题

引理一若点M、N是圆C:x2+y2=r2上关于x轴对称的两点，点P是圆C上异于M、N的任意一点，且直线MP、NP分别与x轴交于点R、S，则|OR|·|OS|=r2.

我们把它推广到椭圆，双曲线 ，抛物线，同样也具有定理关于数轴对称点的定值.

所以|OR|·|OS|=|xR|·|xS|=|xR·xS|=a2．

定理中的点M、N关于x轴对称，当点M、N关于y轴对称时，|OR|·|OS|仍是定值.

推论2的证明与推论1的证明类似，证明略．

经过进一步研究，关于椭圆的这个性质，类似地可以推广到双曲线.

推论3、推论4的证明与定理的证明类似．

但这个关于定值的性质对抛物线不成立，在抛物线中|OR|·|OS|的取值与点P、M的位置有关．

推论5若点M、N是抛物线C:y2=2px上关于x轴对称的两点，点P是抛物线C上异于M、N的点，直线MP、NP分别与x轴交于点R、S，设点M、P在x轴上的射影是H、Q，则|OR|·|OS|=|OH|·|OQ|(O为坐标原点)．

∴|OR|·|OS|=|xR·xS|=|x1x0|．

则|OR|·|OS|=|OH|·|OQ|．

因此，只有在有心圆锥曲线中，|OR|·|OS|是一个定值.

二、圆锥曲线关于点的轨迹方程的定值问题

证明设M(x0,y0)，椭圆C的切线方程为y=kx+m.

因为M(x0,y0)在椭圆C的切线y=kx+m上，所以y0=kx0+m……②.

由①、②得：(y0-kx0)2=b2+a2k2,

所以点M的轨迹方程为x2+y2=a2+b2.

证明设M(x0,y0)，若其中一条切线的斜率不存在，双曲线不存在与之垂直的切线，所以可设双曲线C的切线方程为y=kx+m.

因为M(x0,y0)在双曲线C的切线y=kx+m上，所以y0=kx0+m……②.

由①、②得：(y0-kx0)2=a2k2-b2,

三、圆锥曲线关于某点切线方程的定值问题

引理三过圆x2+y2=r2(r>0)上一点M(x0,y0)的切线方程为xx0+yy0=r2.

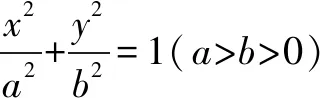
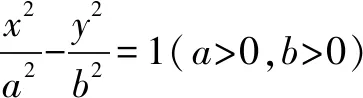
推论3 过抛物线y2=2px(p>0)上一点M(x0,y0)的切线方程为y0y=p(x+x0).

证明(1)y2=2px(p>0)两边求导得