初中数学教学中问题的有效性设置

四川省宜宾市第二中学校，四川宜宾 644000

1 设计渐进性的问题，启迪学生的思维发展

在教学过程中，课堂提问是重要的教学手段，也是教学启发性的集中体现，教师要通过层层深入提问，为学生创造学会解决一类问题的条件，启迪学生的思维发展。

案例一学习了勾股定理后“求最短路程”问题

问题1 如图，四边形ABCD是矩形，A点有一只蚂蚁，它想吃到C点处的食物，问这只蚂蚁在矩形ABCD 上需要爬行的最短路程为多少？（AD ＝6、AB ＝8）

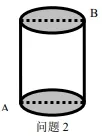
问题2 如图所示，有一个高为12cm，底面半径为3cm的圆柱，在圆柱下底面的A点有一只蚂蚁，它想吃到圆柱上底面上与A点相对的B点处的食物，问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米？

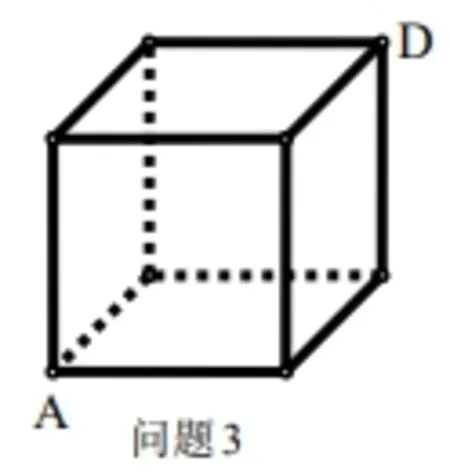
问题3 如图的棱长为10cm的正方体盒子，蚂蚁从A点到达B点需要爬行的最短路程是多少？

2 设计开放性的问题，彰显学生的个性差异

学习是学生内心感受的过程，学生解决一道带有一定难度的问题，要经历一个较为复杂的思维过程。所以，教师要经常提出一些开放性的问题，为每个学生提供发挥的空间，以形成其独立思考的习惯，彰显学生的个性。让每个学生都能够体验数学的快乐，享受成功的喜悦。

案例二 在“探索规律”的数学活动课，设计了如下问题.

问题：在一次围棋单循环比赛中，即每位选手都与其余选手比赛一局。(1)设参加比赛的人数为n，试用关于n的代数式表示这次比赛的总局数； (2)若n ＝5，求第(1)问所列的代数式的值，并说明这个值的实际意义。

1 我们把队员排成一行，第一个队员进行了(n-1)局，第二个队员进行了 (n-2)局，以此类推，比赛总数就是：l+2+3+…+(n-1)=false局。

2 当n ＝5时，一共进行了10局，表示有5个队员共进行了10局比赛。

问题拓展1.若某选手中途退出了比赛，结果比赛只进行了25局，问有多少人参加比赛？中途退出的这名选手放弃了多少局比赛？

点拨：设有n位选手参加比赛，中途退出的这名选手放弃了x局比赛。这样，就可以得到false ＝25 ＋x，即n(n-1)=50+2x，其中n，x都是整数，且x＜n-l.

得出：我发现要把50+2x 写成两个连续的整数的积，只能是8×7 ＝50+2×3，所以n ＝8，x ＝3.也就是有8位选手参加比赛，一位选手放弃了3局比赛。

问题拓展2.在生活中、数学中还有很多利用false 计算的问题。

（1）一条线段上有n个点(包括两个端点)，一共可以形成多少条线段？

（2）有公共端点的n 条射线，一共可以形成多少个角？

（3）同学见面时每两人都握一次手，握手的总次数是多少？

（4）班上共有n人，老师要从中选2位同学去参加公益活动，共有多少种不同的组合？

教学中利用原有的问题进行变式、扩展，围绕问题层层深入剖析，不仅能收到很好的教学效果，而且对于保持学生思维的活跃性，开阔学生的视野都能起到积极的作用。

一堂成功的课离不开精心设计的课堂提问，而有效的提问，就是要把问题设在重点处、关键处、疑难处，从而充分地调动学生的思维，极大地提高数学课堂的教学效率。有效的提问能激发学生学习的积极性、主动性和创造性，也能使学生在讨论中迸发出智慧的火花，使整个课堂焕发出思维的活力，真正让学生感到自己是课堂的主人。