结构-地震动双随机的隔震结构倒塌鲁棒性分析

时晨 杜永峰

摘   要：为分析基于结构及地震动双随机的隔震结构竖向连续倒塌鲁棒性，依据二次四阶矩可靠度理论提出随机鲁棒性指标，通过对比分析隔震结构考虑结构随机、地震动随机性以及同时考虑结构-地震动随机性的鲁棒性指标，揭示随机性对隔震结构竖向连续倒塌鲁棒性的影响，以及PGA对隔震结构抗竖向连续倒塌鲁棒性产生的作用.研究结果表明：基于可靠度的随机鲁棒性指标可定量评估隔震结构抗竖向连续倒塌能力;若仅考虑结构随机或地震动随机，均会高估结构抗竖向连续倒塌能力;此外，随PGA增大，结构抗竖向连续倒塌鲁棒性下降，强震作用下，隔震结构极可能发生竖向连续倒塌现象.

关键词：双随机;连续倒塌;鲁棒性;可靠度;隔震结构

中图分类号：TU352.1                      文献标志码：A

文章编号：1674—2974（2019）09—0011—10

Abstract：To analyze the vertical collapse robustness of isolated structures， considering double randomness of structure and seismic wave， a random robustness index was proposed based on the reliability theory. Through analyzing and contrasting the random robustness indexes of different randomness， the influence of randomness on the vertical progressive collapse robustness of isolated structures was revealed. In addition， the influence of PGA on the vertical progressive collapse robustness of isolated structures was studied. And the following results were obtained： The random robustness index can be effectively used for quantitative evaluation of the vertical progressive collapse ability of isolated structures. If only considering random ness of structures or seismic wave， it may overestimate the ability of the structure. The robustness of the isolation structure decreases with the increase of PGA. Under strong seismic， isolation structures are more prone to vertical progressive collapse.

Key words：double randomness;progressive collapse;robustness;reliability;isolated structure

由結构局部破坏而引发连续倒塌一般都会带来严重的后果，因而成为土木工程领域的国际热点.自“英国Ronan point公寓垮塌”“9.11”等事件以来，国内外学者开始就结构连续倒塌问题展开了大量研究.欧美国家均陆续将结构抗连续倒塌设计纳入结构设计规范规程[1-3]，我国首部抗倒塌设计规范也于2015年5月1日起开始实施[4].目前对连续倒塌的研究多针对于完好结构在地震作用下的“侧向增量连续倒塌”，而对结构遭遇损伤后，发生竖向连续倒塌的问题，近年来才受到关注. 尤其针对于隔震结构，其全部竖向及水平荷载均由数量非常有限的若干个隔震支座承担，结构竖向稳定性和抗倾覆能力都依靠隔震支座维持.隔震层水平刚度及其对上部结构转动约束能力均较小，这就降低了隔震层抗连续倒塌的冗余度. 震害调查结果显示[5]，地震作用下，结构倒塌破坏的过程即构件损伤累计到达失效的过程. 当隔震结构受到地震作用产生损伤，极可能诱发隔震支座竖向支承约束失效，并引起与之相邻区域的隔震支座所承受的竖向荷载剧烈增加[6].由于损伤支座周围的隔震支座不能提供足够的抗侧力，即使在竖向荷载作用下能维持暂态平衡，但稍有地震作用都极易导致结构发生竖向连续倒塌现象[7].因此，研究隔震结构在地震作用下产生初始损伤后，结构的抗竖向连续倒塌能力尤为必要.

结构鲁棒性指在发生偶然事件时对结构造成局部损伤的条件下，结构体系具有不发生整体失效后果与局部损伤原因不成比例破坏的一种能力[8].其体现了结构对局部破坏的不敏感性，是对结构性能更高层次的要求.结构的连续倒塌就是典型的不成比例破坏，因此鲁棒性问题与连续倒塌直接相关.对各类结构鲁棒性的分析和评判指标的探索，在结构连续倒塌研究领域是个相对新鲜的重要议题.Baker等[9]、Husain等[10]、Starossek等[11]、Smith[12]分别基于结构刚度、损伤、能量理论、风险概率及结构相应灵敏度提出了不同的结构鲁棒性评价指标，并对其适用性进行了比较和分析.吕大刚等[13]、宋鹏彦等[14]给出了结构鲁棒性的新定义，将结构鲁棒性的定量测度进行分类，并针对结构的抗震鲁棒性进行了定量评价;杜永峰等[15-16]对隔震层和上部结构两个子系统连续倒塌进行数值模拟，并对隔震结构抗连续倒塌能力进行定性评判.

目前针对鲁棒性的研究大多未考虑随机性的影响，但事实上，鲁棒性其本质具有随机性.首先，地震动不确定性对地震倒塌有较大的影响，吕大刚等[17]、施炜等[18]学者研究表明结构的抗地震倒塌能力与地震动随机性密切相关. 其次，结构自身也存在诸多不确定因素，于晓辉等[19]研究表明结构的随机性会使得结构抗地震倒塌能力的对数标准差增加.特别值得注意的是，当结构临近倒塌时，会出现地震动随机性与结构随机性的耦合放大效应[19-20]，这将对结构连续倒塌鲁棒性产生极大的影响. 因此，考虑结构及地震动双随机的结构抗连续倒塌鲁棒性研究尤为重要.

本文基于二次四阶矩可靠度理论提出考虑结构-地震动双随机的评估隔震结构抗竖向连续倒塌鲁棒性方法，利用结合Pushover的备用荷载路径法，模拟地震作用下隔震支座失效的过程，对比分析了隔震结构考虑结构随机、地震动随机及结构-地震动双随机的鲁棒性指标，揭示了随机性对隔震结构抗竖向连续倒塌鲁棒性的影响，以及PGA对隔震结构抗竖向连续倒塌鲁棒性产生的作用.

1   基于可靠度的随机鲁棒性指标

若考虑结构及地震动的随机性，本质上结构的鲁棒性也是不确定的.随机可靠度理论利用适当的数学方法将随机不确定性与结构的可靠性联系起来，故本文利用具有较高精度的二次四阶矩法得到可靠度指标，以此来描述隔震结构倒塌鲁棒性.

1.1   连续倒塌极限状态方程

将隔震结构的最大竖向荷载作为结构的整体竖向极限承载能力，利用荷载系数α描述结构最大竖向荷载，则完好结构及损伤结构在竖向荷载作用下的极限状态方程分别为[14]：

1.2   基于最大熵原理的二次四阶矩法可靠度指标

1.3   双随机鲁棒性指标

得到完好及损伤结构的可靠度指标后，利用可靠度指标计算出结构的鲁棒性系数，如式（12）[22]所示：

该指标的取值范围为[0，∝]，取值越大表明结构的鲁棒性越强.结构的倒塌极限为1，当该值小于1时，表明结构发生连续倒塌.

2   隔震结构多向动力耦合分析方法

2.1   隔震结构的Pushover分析方法

为分析隔震结构在地震作用下的响应，可采用Pushover分析方法.考虑到在地震中结构受到往复振动作用，因此采取循环往复加載的推覆方式.即对结构进行正向加载至目标位移—卸载，反向加载至目标位移—卸载，完成一次循环.这种循环往复的加载方式可以得到整个循环过程中结构构件的内力和变形、塑性铰的形成和节点转角的变化，从而可以更加准确地模拟地震过程中结构的损伤及耗能情况[23].

隔震结构由于其隔震层刚度较小，上部结构可作为刚体，若在上部结构任何部位施加水平荷载，隔震层均会产生相应位移.而传统Pushover分析方法的水平分布力计算方法中并未考虑结构竖向刚度不均匀的影响，因此，传统Pushover分析方法并不适用于隔震结构.为使Pushover分析方法适用于隔震结构，可在水平分布力的计算中引入刚度调整系数，如式（13）所示[6]：

用隔震结构Pushover方法对本文中隔震结构算例其中一组样本进行水平地震作用响应分析并与非线性动力时程方法进行对比，以验证该方法的正确性，分析结果如图1所示.

从图1可以看出，隔震结构的Pushover分析和非线性时程分析计算得到的楼层位移沿楼层高度的变化规律基本一致，楼层位移的最大误差为1.53%.隔震支座滞回曲线形状接近，计算滞回环面积所得隔震支座累计耗能误差为1.06%.由此可见，无论是结构位移还是隔震层耗能，两者之间的误差均较小，因此，采用隔震结构Pushover分析方法可以用于隔震结构的地震响应分析.

2.2   结合Pushover分析的备用荷载路径法

将Pushover分析方法引入备用荷载路径法中，模拟地震作用下结构发生竖向连续倒塌的过程，该过程可同时考虑水平地震响应及不平衡竖向荷载突加冲击作用.分析步骤如下：

1）将结构竖向荷载（D+0.25L）逐步施加于完好结构;2）根据推覆目标对完好结构进行Pushover分析;3）在竖向荷载和 Pushover水平推覆力共同作用下，提取失效隔震支座的轴力P0和剪力Q0，从原始结构中拆除初始失效隔震支座（隔震支座的建模采用单点模型，不考虑高度的影响，因此，在计算中忽略弯矩的影响），将轴力和剪力反向加在相应位置.4）在竖向荷载和Pushover分析共同作用下，将结构第一次推至最大目标位移时，认为隔震支座受到地震作用造成竖向支承发生初始失效，此时使初始失效隔震支座的轴力P0和剪力Q0在极短时间t1内衰减到零.从而模拟支座在地震过程中突然失效的过程. 荷载施加过程如图2所示.

3   最可能失效隔震支座识别

地震作用下，构件的失效为低周疲劳破坏，判别最易失效的隔震支座采用累计损伤极限状态

法[15]. 根据场地条件，从地震动记录库中随机抽取n条地震动记录，与模型样本组成结构-地震动样本，对每一个样本进行非线性时程分析，计算各隔震支座损伤指数.隔震支座损伤指数计算方法，如式（15）所示[24].

利用二次四阶矩法计算每个支座的可靠度指标，最小者为最易失效支座.

4   双随机竖向连续倒塌鲁棒性分析流程

利用结合Pushover的备用荷载路径法，模拟地震作用下隔震支座失效的过程，利用竖向随机IDA分析得到结构极限荷载系数，用二次四阶矩法计算结构竖向连续倒塌可靠度，进而计算结构鲁棒性指标，具体流程如下：

1）建立有限元模型;2）确定结构及隔震支座随机变量的统计参数和分布类型;3）利用拉丁超立方原理进行抽样，形成结构样本;4）随机抽取地震动，与结构形成结构-地震动样本;5）判断最易失效隔震支座，利用结合Pushover的备用荷载路径法拆除支座;6）对完好及损伤结构进行竖向IDA分析得到结构竖向极限荷载系数;7）求取完好及损伤结构功能函数的前四阶统计矩;8）利用二次四阶矩法计算完好结构及损伤结构可靠度;9）计算结构基于可靠度的随机鲁棒性指标，判断结构是否发生竖向连续倒塌.

5   算例分析

5.1   算例模型

本文以一工程实例为研究背景.该结构的抗震设防类别为乙类，抗震设防烈度8度（0.2g），设计地震分组第三组，场地类别Ⅱ类. 根据《建筑抗震设计规范》（GB 50011—2010）[25]对结构进行设计.隔震支座采用LRB600：有效直径为600 mm，竖向刚度为2 312 kN/mm，水平刚度为1 641 kN/m，等效阻尼比为0.15.梁、柱纵筋均采用HRB400，混凝土强度等级为C30.本结构共7层，各层层高均为3.3 m. 平面示意图及截面配筋图如图3所示.

利用有限元软件SeismoStruct建立结构模型.模型梁柱均采用infrmFBPH单元（基于力的塑性铰框架单元），隔震支座采用Link单元.

采用概率模型描述上部结构参数的随机性，如表1所示.由于目前针对隔震支座各参数的概率密度函数随机性的描述较少，故采用凸集模型[26]来描述隔震支座的随机性，其基本随机变量如表2所示.

根据工程场地条件，从强震记录数据库中挑选符合或与工程场地条件类似的地震动记录，组成场地地震动样本库，利用随机模型，依次从近场脉冲、近场非脉冲、远场地震动记录中共随机抽取20条地震动记录，如表3所示.

在得到各参数的随机变量后，可形成样本空间：1）根据结构及支座基本参数分布类型，每个参数生成1 000个样本，共形成8×1 000个样本.利用拉丁超立方原理，抽取20次，共形成20个结构样本. 2）将抽取的20条地震波随机与结构样本一一对应，形成20个结构-地震动样本.

5.2   最易失效支座判别

利用本文提出的隔震支座累计损伤识别方法，将抽取的20条地震动PGA均调至0.4g，地震动输入方向沿结构平面X方向，对每一样本进行动力时程分析，計算各支座损伤指数. 将结果代入累积损伤极限状态方程，利用二次四阶矩法计算完好结构各支座的可靠度指标，列于图4中.

从图4中可以看出，支座B2可靠度值最小，可见其在地震作用下最易损伤，判定支座B2为算例模型中最易失效的隔震支座.

5.3   鲁棒性分析

5.3.1   仅考虑结构随机性

分析仅考虑结构随机性的隔震结构抗竖向连续倒塌鲁棒性时，分别计算考虑地震作用及不考虑地震作用两种工况作为对比.

隔震结构不考虑地震作用时，选择抽取的20组结构样本，采用传统备用荷载路径法拆除最易失效支座B2，仅考虑支座突然失效引起的竖向不平衡荷载作用.

考虑地震作用时，选取地震动“Imperial Valley-06”，与各结构样本一一对应形成20组随机结构样本.采用本文提出的结合Pushover的备用荷载路径法拆除B2支座.同时考虑水平地震响应及不平衡竖向荷载突加冲击作用.计算水平分布力时将地震动PGA调至0.4g，地震动输入方向为沿结构平面X向.

将所有竖向位移幅值Z和所有样的荷载系数α绘制成竖向IDA 曲线，如图5所示.

从图5中可以看出，随着节点竖向位移增大，荷载系数逐渐增大，达到峰值后，荷载系数几乎不再增大.不考虑地震作用时，各损伤结构荷载系数范围在 2.35～3.80之间;当同时考虑地震作用时，各损伤结构荷载系数范围在1.98～3.59之间，可见考虑地震作用后结构的荷载系数明显减小.降低幅度为最大15.78%，最小2.89%.

结合完好及损伤结构极限状态方程，利用泰勒级数展开法，得到完好及损伤结构功能函数前四阶统计矩信息，如表4所示. 利用二次四阶矩法，计算结构可靠度，进而得到隔震结构随机鲁棒性指标，如表5所示.

从表4中可以看出，考虑地震作用后，完好及损伤结构的功能函数均值从3.675和1.733下降为3.161和1.450，变异系数分别从0.199和0.272增长为0.231和0.33，表明考虑地震作用后，功能函数值更加离散，抗竖向连续倒塌可靠度降低.从表5中可以看出，考虑地震作用后，完好结构与损伤结构的可靠度均有下降，鲁棒性指标也下降了2.78%.可见，结构在地震作用中产生损伤，累计损伤将会加大结构竖向连续倒塌的可能.在分析结构竖向连续倒塌时，应计入水平地震作用，否则可能会高估结构抗竖向连续倒塌鲁棒性.

5.3.2   仅考虑地震动随机性

从20组结构样本中抽取一组结构样本，与20条地震波一一对应，形成20组随机地震动样本.采用结合Pushover的备用荷载路径法拆除B2支座.计算水平分布力时将地震动PGA调至0.4g，地震动输入方向为沿结构平面X向.

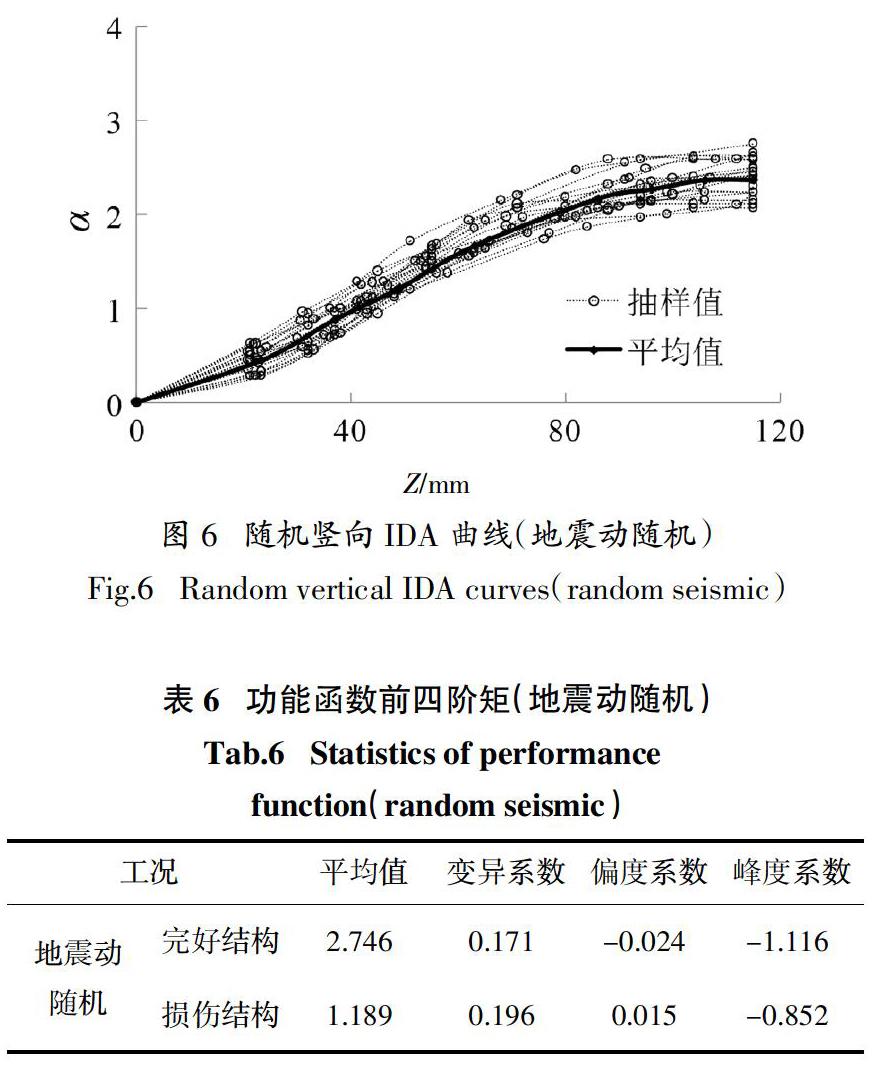
将所有竖向位移幅值Z和所有样本的荷载系数α绘制成竖向IDA 曲线，如图6所示.

从图6可以看出，仅考虑地震动随机的IDA曲线趋势与仅考虑结构随机时类似，荷载系数范围在2.064～2.924之间，随机IDA曲线较为集中，可见其离散性较小.

计算结构功能函数前四阶统计矩列于表6中，计算结构鲁棒性系数列于表7中.

從表6中可以看出仅考虑地震动随机性，完好和损伤结构变异系数分别为0.168和0.196，相较于考虑结构随机有较大幅度减小，结构功能函数离散性下降，计算得出结构可靠度较大.鲁棒性指标计算结果与仅考虑结构随机较接近，仅相差0.04%.可见，地震动随机性对隔震结构竖向连续倒塌影响相较于结构随机性较小.

5.3.3   结构及地震动双随机

将20组结构样本与20条地震波一一对应，得到20组结构-地震动样本.采用结合Pushover的备用荷载路径法拆除B2支座.计算水平分布力时将地震动PGA调至0.4g，地震动输入方向为沿结构平面X向.

将所有竖向位移幅值Z和所有样本的荷载系数α绘制成竖向IDA 曲线，如图7所示.

从图7可以看出，考虑结构及地震动双随机的IDA曲线趋势与仅考虑结构随机时类似，荷载系数范围在1.90～3.53之间，类比仅考虑结构随机最小及最大下降幅度分别为0.1%和14.28%.

计算结构功能函数前四阶统计矩列于表8中，计算结构鲁棒性系数列于表9中.

从表8中可以看出，当同时考虑结构及地震动双随机后，完好和损伤结构变异系数分别增长为0.254和0.361，说明结构功能函数更加离散，结构失效概率增长，可靠度更低.鲁棒性指标下降了5.33%.可见地震动随机与结构随机的耦合，有一定的放大效应，若只考虑结构随机性，可能会高估结构连续倒塌鲁棒性.

将结构鲁棒性系数及倒塌临界值共同作于图8中，结构的倒塌极限为1，当该值小于1时，表明结构发生连续倒塌.

从图8中可以直观看出，本文算例模型在地震动为0.4g时，仅考虑结构随机、仅考虑地震动随机和结构及地震动双随机的3种工况均高于倒塌临界，并未发生竖向连续倒塌. 考虑地震作用后结构鲁棒性降低，当考虑双随机时，结构抗竖向连续倒塌鲁棒性系数更低，说明结构更易发生竖向连续倒塌现象.

5.4   PGA对竖向连续倒塌鲁棒性影响

根据文中所得结构-地震动样本，将样本中的地震动峰值分别调整为0.4g、0.6g、0.8g、1.0g、1.2g和1.4g，计算结构在不同PGA下功能函数四阶矩，接着计算出结构的鲁棒性指标如表10所示.

从表10中可以看出，随着PGA增大，结构发生竖向连续倒塌的概率增大，可靠度降低.当PGA达到1.4g时完好结构可靠度从9.01下降到1.976;损伤结构从4.73下降到0.276，下降幅度分别为78%和94%.这是由于当PGA增大，结构在地震作用中的累计损伤增大，致使结构发生竖向连续倒塌的概率增大.

将鲁棒性指标及倒塌极限共同表示于图9中，判断在不同PGA下是否发生竖向连续倒塌.

从图9可以直观看出，随着PGA的增大，隔震结构在地震作用下竖向连续倒塌鲁棒性下降，当PGA增大到1.4g时，鲁棒性指标为1.136，结构基本到达倒塌临界值，说明结构很可能发生竖向连续倒塌.可见，在结构遭遇极强震时，结构有极大可能发生竖向连续倒塌现象，但目前，我国并未对竖向连续倒塌设计方法有明确规定，应引起抗震设计人员的重视.

6   结   论

本文基于二次四阶矩可靠度理论提出考虑结构-地震动双随机的评估隔震结构抗竖向连续倒塌鲁棒性方法，对比分析了隔震结构考虑结构随机、地震动随机及结构-地震动双随机的鲁棒性指标，揭示随机性对隔震结构抗竖向连续倒塌鲁棒性的影响，并研究了PGA对隔震结构抗竖向连续倒塌鲁棒性产生的作用，主要结论如下：

1）基于二次四阶矩可靠度理论的随机鲁棒性

指标可定量评估隔震结构考虑结构及地震动双随机的竖向连续倒塌能力，为结构设计及震后加固提供直观依据.

2）分析地震作用下，隔震结构发生竖向连续倒塌时，若不考虑地震作用，可能会高估结构抗竖向连续倒塌的能力，因此，应同时考虑水平地震响应和竖向不平衡荷载冲击对整个结构损伤的影响.

3）结构随机性对于隔震结构竖向连续倒塌鲁

棒性的影响大于地震动随机性，但地震动随机性的影响也不容小视，考虑结构-地震动双随机时，有耦合放大作用，因此，在分析地震作用下隔震结构竖向连续倒塌鲁棒性时应同时考虑结构及地震动随机性的影响.

4）随着PGA的增大，对结构造成的损伤增大，结构抗竖向连续倒塌鲁棒性下降，尤其强震作用下，结构支座初始失效后，在多向动力耦合激励下，隔震结构极可能发生竖向连续倒塌现象.设计人员应予以重视.

参考文献

[1]    DraftprEN1991-1-7 Eurocode1-actions on structures. part1.7： General actions-accidental actions [S]. Brussels：European Committee for Standardization，2005：5—9.

[2]    GSA2003 Progressive collapse analysis and design guidelines for guidelines for new federal office buildings and major modernization projects [S]. Washington D C：General Service Administration，2003：16—20.

[3]    UFC 4-023-03 Design of buildings to resist progressive collapse. U.S. department of defence [S]. Washington D C： Unified Facilities Criteria，2005：7—11.

[4]    CECS 392—2014 建筑结构抗倒塌设计规范[S].北京：中国计划出版社，2015：4—16.

CECS 392—2014 Code for anti-collapse design of building structures [S]. Beijing：China Planning Press，2015：4—16. （In Chinese）

[5]    熊立红，兰日清，王玉梅，等. 芦山7.0级强烈地震建筑结构震害调查[J]. 地震工程与工程振动，2013，33（4）：35—43.

XIONG L H，LAN R Q，WANG Y M，et al. Earthquake damage investigation of structures in 7.0 Lushan strong earthquake [J]. Journal of Earthquake Engineering and Engineering Vibration，2013，33（4）：35—43. （In Chinese）

[6]    黃小宁.框-剪隔震结构抗扭设计及双随机地震倒塌可靠度研究[D]. 兰州：兰州理工大学土木工程学院，2017：87—107

HUANG X N. Torsional-resistance design and study on seismic collapse reliability based on double random of frame-shear-wall isolated structure [D]. Lanzhou：School of Civil Engineering，Lanzhou University of Technology，2017：87—107. （In Chinese）

[7]    包超. 竖向不规则基础隔震结构连续倒塌机制及抗倒塌性能研究[D]. 兰州：兰州理工大学土木工程学院，2015：123—135

BAO C. Research on progressive collapse mechanism and resistance performance of vertically irregular base-isolated structure [D]. Lanzhou：School of Civil Engineering，Lanzhou University of Technology，2015：123—135. （In Chinese）

[8]    吕大刚，宋鹏彦，崔双双，等. 结构鲁棒性及其评价指标[J]. 建筑结构学报，2011，32（11）：44—54.

L？譈 D G，SONG P Y，CUI S S，et al. Structural robustness and its assessment indicators [J].Journal of Building Structures，2011，32（11）：44—54. （In Chinese）

[9]   BAKER J W，SCHUBERT M，FABER M H. On the assessment of robustness [J]. Structural Safety，2008，30 （3）：253—267

[10]  HUSAIN M，TSOPELAS P. Measures of structural redundancy in reinforced concrete buildings. I：redundancy indices [J]. Journal of Structural Engineering，ASCE，2004，130（11）：1651—1658.

[11]  STAROSSEK U，HABERLAND M. Approaches to measures of structural robustness [J]. Structure & Infrastructure Engineering，2011，7（7/8）：625—631.

[12]  SMITH J W. Structural robustness analysis and the fast fracture analogy [J]. Structural Engineering International，2006，16（2）：118—123.

[13]  吕大刚，崔双双，李雁军，等.基于备用荷载路径Pushover方法的结构连续倒塌鲁棒性分析[J].建筑结构学报，2010，31（S2）：112—118.

L？譈 D G，CUI S S，LI Y J，et al. Robustness analysis for progressive collapse of structures using ALP -based Pushover analysis approach [J]. Journal of Building Structures，2010，31（S2）：112—118. （In Chinese）

[14]  宋鹏彦，吕大刚，崔双双. 地震作用下钢筋混凝土框架结构连续倒塌极限状态可靠度分析[J]. 建筑结构学报，2013，34（S2）：15—22.

SONG P Y，L？譈 D G，CUI S S. Reliability analysis of progressive collapse limit state of reinforced concrete frame structure under earthquakes [J]. Journal of Building Structures，2013，34（S2）：15—22. （In Chinese）

[15]  杜永峰，黃小宁，李慧. 基于变形及滞回耗能的RC框剪结构地震损伤评估[J].湖南大学学报（自然科学版），2017，44（11）：38—45.

DU Y F，HUANG X N，LI H. Deformation and hysteretic energy-based seismic damage evaluation of frame-wall structures [J]. Journal of Hunan University （Natural Sciences），2017，44（11）：38—45. （In Chinese）

[16]  杜永峰，包超，张尚荣，等. 竖向不规则RC框架抗竖向连续倒塌鲁棒性分析[J] .土木工程学报，2014，47（S2）：101—107.

DU Y F，BAO C，ZHANG S R，et al. Robustness analysis of the vertical progressive collapse resistance of vertically irregular RC frame [J].China Civil Engineering Journal，2014，47（S2）：101—107. （In Chinese）

[17]  吕大刚，于晓辉，王光远. 单地震动记录随机增量动力分析[J].工程力学，2010，27（S1）：53—58.

L？譈 D G，YU X H，WANG G Y. Single record random incremental dynamic analysis [J]. Engineering Mechanics，2010，27（S1）：53—58. （In Chinese）

[18]  施炜，叶列平，陆新征，等. 不同抗震设防RC框架结构抗倒塌能力的研究[J]. 工程力学，2011，28（3）：41—48，68.

SHI W，YE L P，LU X Z，et al. Study on the collapse-resistant capacity of RC-frames with different seismic fortification level[J]. Engineering Mechanics .2011，28（3）：41—48，68. （In Chinese）

[19]  于晓辉，吕大刚. 考虑结构不确定性的地震倒塌易损性分析[J].建筑结构学报，2012，33（10）：8—14.

YU X H，L？譈 D G. Seismic collapse fragility analysis considering structural uncertainties [J]. Journal of Building Structures，2012，33（10）：8—14. （In Chinese）

[20]  樊剑，龙晓鸿，赵军. 近场地震下隔震结构基底发生碰撞的鲁棒易损性曲线计算[J]. 工程力学，2014，31（1）：166—172.

FAN J ，LONG X H，ZHAO J. Calculation on robust fragility curves of base-isolated structure under near-fault earthquake considering base pounding [J]. Engineering Mechanics，2014，31（1）：166—172. （In Chinese）

[21]  李云贵，赵国藩. 结构可靠度的四阶矩分析法[J].大连理工大学学报，1992，32（4）：455—459.

LI Y G，ZHAO G F. Reliability analysis of structures based on maximum entropy theory [J]. Journal of Dalian University of Technology，1992，32（4）：455—459. （In Chinese）

[22] FRANGOPOL D M， CURLEY J P. Effects of damage and redundancy on  structural reliability [J]. Journal of Structural Engineering，ASCE，1987，113（7）：1533—1549.

[23]  侯爱波，汪梦甫.循环往复加载的Pushover分析方法及其应用[J].湖南大学学报（自然科学版），2003，30（3）：145—152.

HOU A B，WANG M F. Analysis method and application of Pushover loading in circles [J]. Journal of Hunan University（Natural Sciences），2003，30（3）：145—152. （In Chinese）

[24]  杜东升，王曙光，刘伟庆，等. 隔震结构损伤性能与可靠度研究[J].振动与冲击，2016，35（1）：222—227.

DU D S，WANG S G，LIU W Q，et al. Reliability based damage performance of base isolated structure[J]. Journal of Vibration and Shock，2016，35（1）：222—227. （In Chinese）

[25]  GB 50011—2010   建筑抗震设计规范[S].北京：中国建筑工业出版社，2010：8-16，240—246.

GB 50011—2010 Code for design of concrete structures[S]. Beijing：China Architecture & Building Press，2010：8—16，240—246.（In Chinese）

[26]  樊剑，龙晓鸿，赵军. 计算近场地震作用下隔震结构支座破坏易损性曲线的概率凸集混合模型[J]. 计算力学学报，2014，31（2）：199—204.

FAN J，LONG X H，ZHAO J. A hybrid probabilistic and convex model for caculating the vulnerability curve of the failure of isolation bearing under near-fault earthquake ground motion[J]. Chinese Journal of Computational Mechanics，2014，31（2）：199—204. （In Chinese）