基于多时间尺度的锂离子电池SOC和SOH联合估计
2019-11-20王慧乐叶康龙张顺风
王慧乐 叶康龙 张顺风


【摘 要】为了解决车载锂离子电池运行状态存在未知性和剩余寿命存在不确定性的问题,论文通过运用戴维南等效电路模型对开路电压与电池荷电进行关系拟合,设计了基于多尺度理论的锂离子电池SOC和SOH联合估计方法。论文建立了用于SOH估计的电池容量模型,采用多时间尺度理论将车载电池运行状态和寿命进行综合考虑,准确地预测了锂离子电池动态运行中SOC和SOH的变化,从而使锂离子电池在整车开发过程中实现更为有效地循环利用。
【Abstract】In order to solve the problems of unknown operation status and uncertainty of residual life of lithium-ion batteries on vehicles, the paper uses Thevenin equivalent circuit mode to fit the relationship between the open-circuit voltage and battery charge, and designs a joint estimation method of SOC and SOH for lithium-ion batteries based on multi-scale theory. This paper establishes a battery capacity mode for SOH estimation. The mode uses multi-time scale theory to comprehensively consider the running status and life of onboard batteries, accurately predicts the changes of SOC and SOH during the dynamic operation of lithium-ion batteries, so that the lithium-ion batteries can be recycled more effectively in the process of vehicle development.
【关键词】电池模型;多时间尺度;卡尔曼滤波;荷电状态;健康状态
【Keywords】battery mode; multi-time scale; Kalman filtering; state-of-charge; state-of-health
【中图分类号】TK02 【文献标志码】A 【文章编号】1673-1069(2019)09-0141-04
1 引言
车载蓄电池是驱动电动汽车的主要能量供给单元,除具备车辆整车过程中所需的能量外,也为车载电量供给与控制系统等低压设备提供动力支持[1-2]。同时,与蓄电池能量、功率、倍率特性等相关的性能指标也较为明显地影响了车辆的性能。因此,电池能量管理系统BMS(Battery Management System)及其实时控制模关键技术成为车辆电池性能和电池监控系统优化的研究重点[3-4]。为了实现电动车辆行驶里程的延长和电池组正常充放电的次数与可靠性的提升,车载电池的荷电状态SOC(State-of-Charge)、健康状态SOH(State-of-Health)、可使用寿命RUL(Remaining Useful Life)等问题的估计正逐渐成为研究的热点,国内外学者也将其估计问题作为研究重心。因此,通过SOH的实时在线精确监控,获取车载电池的实时健康状况,能够为车辆电池间的均衡调控提供有效支持[5-6]。电池荷电状态SOC和健康状态SOH的协同管控是判断电池能量管理系统BMS是否均衡的重要指标之一。目前,虽然在电池荷电状态SOC管控方面取得不少成果,但将电池健康状态SOH与电池荷电状态SOC进行协同均衡控制的效果不佳,而且还使车辆的行驶性能大打折扣,从而导致整套车辆电池使用寿命的降低以及其使用安全的未知性增加。从实际整车环境来看,车辆电池的SOC是研究SOH衰减的影响参数之一[7]。
2 基于模型分析的方法
2.1 锂离子电池等效模型
建立和模拟处理老化模型与等效电池模型。在建立模型时,首先确定模型的主要参数,即电池的内部变量、容量、内阻等表征参数。在通过利用建立的模型对SOH进行预测时,虽然可以直接较好地获取电池的SOH,但测量数据具有需要预处理的弊端,较难兼顾高效性与实时性。同时,受限于估计精度的问题,基于等效模型法和电化学法的估计手段同样不能直接用于其他种类的电池。
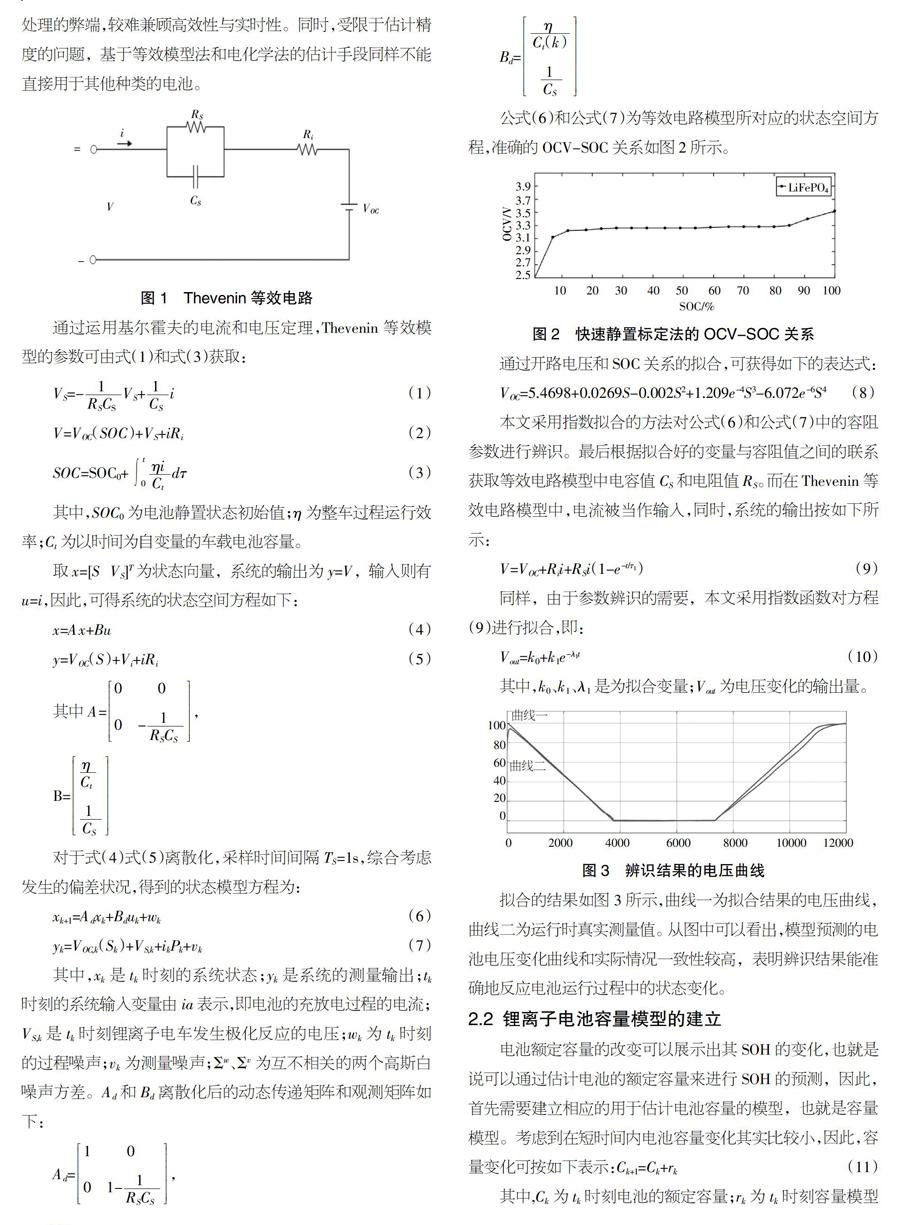
通过运用基尔霍夫的电流和电压定理,Thevenin等效模型的参数可由式(1)和式(3)獲取:
VS=-VS+i (1)
V=VOC(SOC)+VS+iRi (2)
SOC=SOC0+dτ (3)
其中,SOC0为电池静置状态初始值;η为整车过程运行效率;Ct为以时间为自变量的车载电池容量。
取x=[S VS]T为状态向量,系统的输出为y=V,输入则有u=i,因此,可得系统的状态空间方程如下:
x=Ax+Bu (4)
y=VOC(S)+Vi+iRi(5)
其中A=0 0
0
-,
B=
对于式(4)式(5)离散化,采样时间间隔TS=1s,综合考虑发生的偏差状况,得到的状态模型方程为:
xk+1=Adxk+Bduk+wk (6)
yk=VOC,k(Sk)+VS,k+ikPk+vk (7)
其中,xk是tk时刻的系统状态;yk是系统的测量输出;tk时刻的系统输入变量由ia表示,即电池的充放电过程的电流;VS,k是tk时刻锂离子电车发生极化反应的电压;wk为tk时刻的过程噪声;vk为测量噪声;Σw、Σv为互不相关的两个高斯白噪声方差。Ad和Bd离散化后的动态传递矩阵和观测矩阵如下:
公式(6)和公式(7)为等效电路模型所对应的状态空间方程,准确的OCV-SOC关系如图2所示。
通过开路电压和SOC关系的拟合,可获得如下的表达式:
VOC=5.4698+0.0269S-0.002S2+1.209e-4S3-6.072e-6S4 (8)
本文采用指数拟合的方法对公式(6)和公式(7)中的容阻参数进行辨识。最后根据拟合好的变量与容阻值之间的联系获取等效电路模型中电容值CS和电阻值RS。而在Thevenin等效电路模型中,电流被当作输入,同时,系统的输出按如下所示:
V=VOC+Rii+RSi(1-e-t/τ1)(9)
同样,由于参数辨识的需要,本文采用指数函数对方程(9)进行拟合,即:
Vout=k0+k1e-λ1t (10)
其中,k0、k1、λ1是为拟合变量;Vout为电压变化的输出量。
拟合的结果如图3所示,曲线一为拟合结果的电压曲线,曲线二为运行时真实测量值。从图中可以看出,模型预测的电池电压变化曲线和实际情况一致性较高,表明辨识结果能准确地反应电池运行过程中的状态变化。
2.2 锂离子电池容量模型的建立
电池额定容量的改变可以展示出其SOH的变化,也就是说可以通过估计电池的额定容量来进行SOH的预测,因此,首先需要建立相应的用于估计电池容量的模型,也就是容量模型。考虑到在短时间内电池容量变化其实比较小,因此,容量变化可按如下表示:Ck+1=Ck+rk (11)
其中,Ck为tk时刻电池的额定容量;rk为tk时刻容量模型的过程噪声,是均值为零、方差为Σr的高斯白噪声。
一般来讲,电流和端电压能够直接地从一个电池系统中测量获取。因此,在容量预测系统中,本文选择端电压作为系统的输出变量,而由电流充当输入变量。而相应等效电路模型的输出方程也同时是电池容量模型的输出方程,即上文的公式(7)也同样是容量模型的输出方程。
3 多时间尺度理论的锂离子电池SOC和SOH联合估计方法
由于使用环境导致电池的日渐老化和运行时的性能恶化,外在性能上表现为容量能力的下降和功率的降低。目前,对SOH还未有统一的标准定义,在电动汽车电池能量管理中,可通过循环次数、满电饱和状态下电池电压、内阻参数来评估电池的健康状况,若其中的任一变量达到阈值,就可以判定车载电池处于危险运行状态。在本文研究中,以目前公认容量判断手段来计算SOH,即电池在整车使用中可释放的最大电量与车载电池中铭牌标注的出厂容量的比率,如式(12)所示:
SOH=×100% (12)
3.1 多时间尺度EKF模型变换
为减小偏差并简化估计器的计算量,设计了多时间尺度估算方法,实现车辆电池SOC和SOH的联合估计。建立宏观和微观的测量尺度,在宏观尺度上估测车辆电池的额定容量Ck;在变化频繁的微观时间尺度上估测车辆电池的SOC。极化反应电压VS作为宏观尺度变量。将第二部分建立的状态空间模型转换,得:
sk,l+1=Ad·xk,l+Bd·ik,l+wk,l (13)
Ck+1=Ck+rk (14)
yk,l=VOC(Sk,l)-Vsk,l-ik,l·Ri+vk,l=g(xk,l,ik,l)+vk,l (15)
其中,xk,l=[Sk,l Vsk,l]是系统在tk,l=tk,0+l·TS时刻的微观尺度变量,0≤l≤L;L为时间尺度分离量;tk,0=tk-1,L;TS是间隔为1s的采样间隔时间;k和l分别为不同尺度的计数变量;Ck是系统在tk,0时刻电池的额定容量;ik,l是输入变量,即在行车过程中车辆电池在tk,l时刻的电流变化;yk,l=Vk,l是系统观测值,即在tk,l时刻的车辆电池端电压测量值。
3.2 多时间尺度EKF算法
在多时间尺度框架下,在基于EKF预测测车辆电池的SOC和SOH的方法中,车载电池SOC在微观尺度进行观测,而SOH在宏观尺度下进行预计。为研究方便,将EKFx作为对电池荷电状态的微观滤波器,EKFC表示对车载电池容量的宏观估计。多时间尺度EKF的算法步骤如下。
初始時刻t0,0(k=0,l=0):
①多尺度EKF初始化
=E[C] (16)
P=E[(C-)(C-)] (17)
=E[x] (18)
P=E[(x-)(x-)] (19)
对于tk时刻(k=1,2…):
②EKFC的时间更新
[][-]= (20)
P=P+Σ (21)
对于tk-1,l时刻(l=1,2…L):
③EKFx的时间更新
[k-1, l =Ad· +Bd·ik-1,l][k-1, l][-][-] (22)
P=Ad·P·A+Σ(23)
④EKFx的测量更新
K=P·C·[C·P·C+Σ] (24)
[k-1, l =[k-1, l][-]+K·[yk-1,l -g([k-1, l][-],ik-1,l)]][x] (25)
P=[I-K·C]·P (26)
⑤电池状态提取Sk-1,l=[1 0]·k-1, l (27)
⑥时间序列计算
在l=1,2…L时,循环计算步骤③-⑤,可得到k-1, l 和P。
⑦时间尺度转换
k,0=k-1,L (28)
P=P (29)
yk,0=yk-1,L (30)
ik,0=ik-1,L (31)
对于tk时刻(k=1,2…):
⑧EKFC的测量更新
K=P·C·[C·P·C+Σ] (32)
⑨电池额定容量提取
Ck=k (33)
其中,k为Ck的估计值;k-1,l为xk-1,l的估计值;E[*]表示求算术平均数;P为容量预计方差矩阵;P为状态估计误差方差矩阵;[k][-]为容量先验估计值;[k,l][-]为状态先验估计值;P为状态估计误差方差先验估量值;K为状态估计反馈增益矩阵;
K为容量估计反馈增益矩阵;矩阵:
C=
C=[][-]
=+×
C=
x=[][-]=×
4 NEDC工况下的算法验证
举例分析,实例中包括四个市区循环(最大车速50km/h)和一个市郊循环工况(最大车速120km/h),总计时1184s且工况之间间隔30s来模拟真实整车运行状况。进行仿真时,车辆电池SOC初始值为80%,全新电池铭牌标注额定容量为27Ah(SOH=0.93)。为了测试所设计的估计器在初始值有偏差情况下的鲁棒性,将90%设为所设计的估测器的SOC初始值,容量初值为26.3Ah(SOH=0.912)。多时间尺度算法的尺度变量。在宏观时间尺度上每隔对时间更新和测量更新一次,车辆电池SOC测量更新中使用的变量数据是微观EKF中估计得到。
基于ADVISOR仿真平台中的NEDC工况下,车辆电池的端电压和电流变化曲线如图4第一框图所示。在第三框图中,蓝色曲线代表测量车载电池單体端电压曲线,红色曲线代表误差变化。随着运行时间的增加,偏差逐渐减小。可以通过图4第四框图看出SOH的容量变化和偏差曲线变化。在额定容量变化曲线中,在初始时刻容量估计值与实际值有较大偏差,随时间改变误差在逐渐收敛,估测精度偏差始终保持在很小的范围内。
5 结论
本文提出了基于多时间尺度EKF算法对车载锂离子电池SOC和SOH的联合估计方法,分析了多时间尺度EKF算法,其中多时间尺度EKF中的宏观EKF用于额定容量的估计,微观EKF用于SOC的估计。设计出计算频率高而且计算量小的多尺度算法估计器,通过在NEDC工况下进行了算法验证。可以从实验仿真曲线看出,多时间尺度EKF算法可以很准确地测量车辆锂离子电池状态和剩余寿命。
【参考文献】
【1】郑方丹. 基于数据驱动的多时间尺度锂离子电池状态评估技术研究[D].北京:北京交通大学,2017.
【2】周秀文. 电动汽车锂离子电池健康状态估计及寿命预测方法研究[D].长春:吉林大学,2016.
【3】董婷婷. 增程式电动车能量管理及电池寿命研究[D].长春:吉林大学,2013.
【4】文鸿雁. 基于小波理论的变形分析模型研究[D].武汉:武汉大学,2004.
【5】闫莉萍. 多尺度数据融合状态估计算法研究[D].开封:河南大学,2003.
【6】Liu G , Lu L , Fu H , et al.A comparative study of equivalent circuit models and enhanced equivalent circuit models of lithium-ion batteries with different model structures[C]//Transportation Electrification Asia-pacific.IEEE,2014.
【7】刘芳,马杰,苏卫星,等.基于数据驱动EKF算法的电动汽车及插电式混合动力汽车动力电池SOC估计[J].Journal of Central South University,2019,26(06):1402-1415.
