高光谱亚像元定位的线特征探测法
2019-11-20刘照欣赵辽英厉小润陈淑涵
刘照欣,赵辽英,厉小润,陈淑涵
1. 杭州电子科技大学计算机学院,浙江 杭州 310018; 2. 浙江大学电气工程学院,浙江 杭州 310027
传统的硬分类技术[1]大都是在空间分辨率足够高的前提下将每个像元归为一种地物类型。高光谱图像空间分辨率的限制使得混合像元普遍存在,一个像元内可能包含两种或多种不同的地物,因此硬分类技术难以精确反映地物的实际空间分布。基于混合像元分解的软分类技术[2-5]虽然能估计混合像元内各种地物的混合比例(丰度),但仍然无法确定像元内地物的空间分布。亚像元定位能确定每一个混合像元内各种地物的具体空间分布,是一种更适合对高光谱图像进行亚像元级精细地物分类的技术。
目前,很多新的亚像元定位方法被提出,包括线性优化的方法[6-8]、基于软硬属性转换的方法[9-11]、基于神经网络的方法[12-13]、基于地学统计的方法[14-15]和决策层融合的方法[16-17]等。其中,线性优化的方法是近几年研究得比较多的。这类方法首先在像元混合比例已知的前提下,定义一个描述空间相关性的数学模型,将亚像元定位转化为一个线性优化问题。反映空间相关性的数学模型典型的有空间引力模型[18-19]和定位后的区域周长[6-8]。文献[20]以各类区域周长最小为目标分别用模拟退火和像元交换技术进行迭代优化;文献[6]则利用二进制粒子群算法进行优化,结果优于模拟退火优化;文献[8]用改进的二进制量子粒子群(modified binary quantum particle swarm optimization,MBQPSO)迭代优化,相比文献[6]的方法,进一步提高了定位精度。
上述这些方法都没有考虑地物空间分布特征,不能有效处理少量的点状或者线状地物的亚像元定位,容易导致一些离散的点状地物产生聚集性,也难以保证线状地物的连通性。预先判断含线特征的混合像元,并对线面分布的地物采用分而治之的方法进行亚像元定位,可以提高整体亚像元定位精度,如文献[21]兼顾面状和线状分布的地物,使用了特征探测、定位和决策等多个智能体分别实现不同特征的获取、不同特征的定位和最后的优化处理;文献[22]通过图像分割并计算各区域形状密度指数(shape density index,SDI)将地物目标分为面、线、点3类,针对不同的目标使用相应的亚像元定位模型进行分而治之的处理方式,相比基于空间相关性原理的定位方法,所提出的模板匹配方法能更准确地实现线状地物的亚像元定位。以上方法尽管都能提高亚像元定位的精度但是都存在一定的不足,文献[21]提出的最大线性指数(maximum linearization index,MLI)方法采用逐像元线特征探测的策略,能探测所有的线特征,但该方法仍有两点需要改进:①线特征探测所需的直线数量取决于一个参数,不能保证得到最优结果;②没有预先判断混合像元内肯定不可能呈线性分布的地物类型。SDI方法的不足是无法有效探测以亚像元形式存在的线特征,另外SDI在确定混合像元内呈线状分布的地物类别时,没有考虑到混合像元内其他亚像元类别如何确定。
为了解决以上问题,本文提出一种基于完备直线集的最大线性指数法用于判断混合像元内线特征。这种方法与文献[21]相比不用考虑步进角度对结果的影响,与文献[22]相比可以实现亚像元级的线特征探测。试验结果表明本文提出的方法无论从线特征判断的准确性还是时间效率这两方面都优于文献[21]及文献[22]。
1 混合像元内线特征探测
为了判断混合像元内是否存在某类地物的线特征,需要对其邻域像元进行判断。假设目标混合像元记为Pij,其D×D的邻域像元Pi′j′构成像元集为
(1)
式中,符号∧表示逻辑与。为方便后续分析,将混合像元及其邻域放在同一坐标系下,在新的坐标系统中,每个像元Pi′j′用一个1×1的方格表示,则Eij中所有的像元方格构成一个边长为D的正方形区域,区域内每个像元Pi′j′对应的方格为ARi′j′,Eij中所有像元对应的方格集合为
CAij={ARi′j′│(i′→(i′+1)∧j′→(j′+1)),
Pi′j′∈Eij}
(2)
式中,CAij称为像元Pij的控制区域。
要判断混合像元Pij内是否存在线性特征,需对经过Pij的每条可能的直线进行判断。以D=5为例,图1给出了新坐标系中混合像元Pij的控制区域及线性探测示意图[21]。其中含有第c类地物的像元方格用深灰色标记,像元Pij对应小方格的中心点坐标为(i+0.5,j+0.5),L0、Lπ/2、Lθ、L-θ分别为过目标混合像元Pij中心的直线,Lλ表示Lθ和L-θ之间过Pij中心的一条直线。直线L0、Lπ/2将控制区域CAij分成4个象限,其中右上角对应区域为第1象限。为便于描述,以令从直线L0沿Pij的中心逆时针转到其他直线的夹角为正数,则Lθ与L0的夹角为θ=arctan(D)。由于Lθ和L-θ关于直线L0对称,所以L0与L-θ之间的夹角为-θ。记λ为Lλ和L0之间的夹角,显然,过Pij的任一直线Lλ介于Lθ和L-θ之间,因此,-θ≤λ≤θ。
1.1 最大线性指数法[21]
文献[21]提出:直线从Lθ开始以一定的步进角度τ转向直线L-θ,即λ=θ-k1×τ,其中k1为自然数,其取值取决于步进角度的大小。对于每一条直线Lλ,求Lλ经过的方格集与CAij的交集
ARLλ={ARi′j′|ARi′j′∧Lλ≠∅, ARi′j′∈CAij}
(3)
方格集ARLλ对应的像元集为PLλ,对每条直线Lλ求Pij中存在第c类的线特征的可能性
(4)
式中,Gλ(c)是像元集PLλ中类别c的丰度大于0的像元个数;H(c)是邻域像元集Eij中类别c的丰度大于0的像元个数。
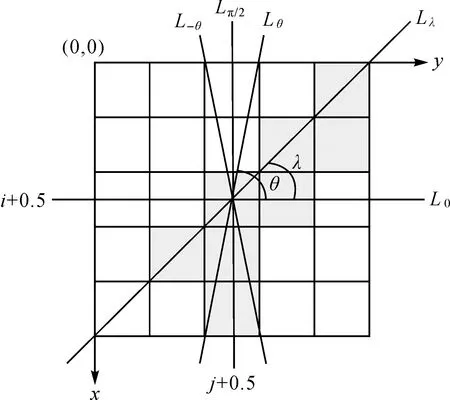
图1 新坐标系中混合像元的Pij控制区域及线性探测(D=5)Fig.1 Control area and linear detection diagram of mixed pixels in the new coordinate system (D=5)
混合像元Pij对应的所有φλ(c)中的最大值称为最大线性指数(maximum linearization index,MLI)[21],即
MLI=φλ′(c′),∃λ′,c′:φλ′(c′)=max{φλ(c),c∈C}
(5)
根据如下规则
MLI≥ρ∧Gλ′(c′)≥D
(6)
判断Pij中是否存在线特征。如果式(6)所述的条件成立,则像元Pij中存在线性特征。其中ρ为阈值,根据经验ρ=0.5。
1.2 基于完备直线集的最大线性指数法
从Lθ到L-θ的所有直线都经过一定的小方格,以每条直线经过的小方格组合为一个方格元素,从Lθ到L-θ的直线所经过的所有可能的方格元素构成一个集合,记为A。如果一个直线集中各直线经过的方格元素构成的集合等于A,则称该直线集为完备直线集。
文献[21]提出的最大线性指数法的结果取决于步进角度τ的选择,直线集不一定是完备的。经过分析后发现:经过混合像元Pij的直线具有一定的规律,因此可以构造完备的直线集。图2给出了D=5时混合像元Pij线特征探测的完备直线集中的部分直线,以Lλ5和Lλ6为例,Lλ5和Lλ6之间的所有直线所经过的小方格组合是一样的,所以该区间内只取一条直线就可以,设取直线L(λ5/λ6)/2。同理,其余区间也可以只取L(λi+λi+1)/2,因此采用该种方式能找到一个完备直线集。下面从理论上分析如何得到完备直线集。
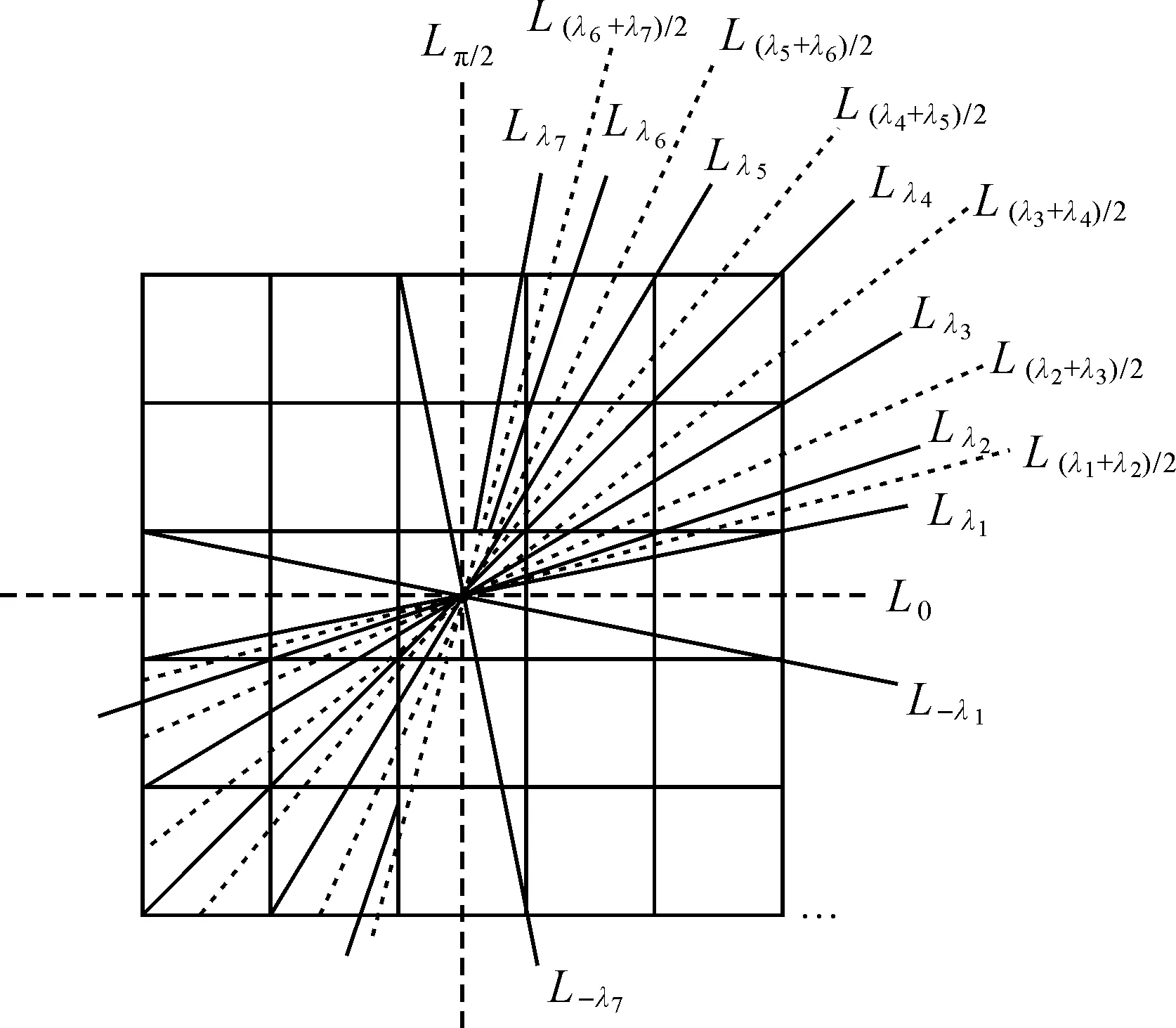
图2 线特征探测的直线集(D=5)Fig.2 A set of lines for linear feature detection (D=5)
先分析混合像元Pij与其控制区域CAij内第1象限的各个方格顶点的连线。
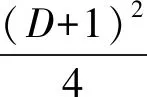
(7)
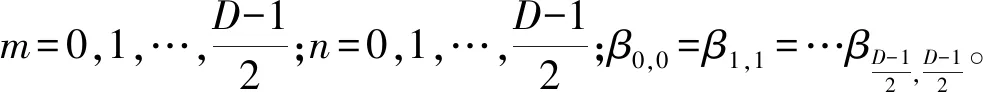
接下来分析Lλi和Lλi+1之间过Pij的直线。
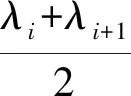
最后,根据对称性,得到过Pij的直线与L0之间的夹角集合为
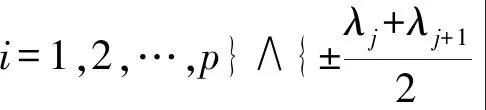
j=1,2,…,p}
(8)
β集合对应的各条直线构成了混合像元Pij内线特征探测的完备直线集。利用完备直线集,参照文献[21],根据式(4)—式(6)计算最大线性指数可以判断Pij内是否含有线性特征。
步进角度τ的选择会影响线特征探测的结果,角度τ过小需要判断的直线多,时间效率低;角度τ过大,线特征探测结果不准确。本文提出的完备直线集的确定,不需要考虑步进角度τ,避免了参数的影响,可以有效提高线特征探测结果的准确性及提高算法的时间效率。
如果能预先判断某个混合像元内肯定不可能呈现线性分布的地物类型,则可以减少计算量。设重建尺度为s,即每一个低分辨率像元被分成s×s个亚像元。因为像元Pij内肯定不存在丰度小于1/s2的地物的线特征,所以,只有Pij(c)≥1/s2的像元Pij内才可能含线状分布的地物。
根据上述分析,混合像元Pij内线特征判断算法的描述如下:
(1) 根据Pij(c)与1/s2的大小关系,确定目标像元Pij内可能呈线状分布的地物类别标签集C={c|Pij(c)≥1/s2}。
(2) 对任意λ∈β,计算Lλ:(x-i)=tan(λ)×(y-j)与CAij的交集PLλ。
(3) 对任意的c∈C,求Eij中类别c的丰度大于0的像元个数H(c)。
(4) 对任意c∈C,求像元集PLλ中类别c的丰度大于0的像元个数Gλ(c),根据式(4),对每条直线Lλ求Pij中存在第c类的线特征的可能性φλ(c)。
(5) 根据式(5)计算最大线性指数MLI。
(6) 最后根据规则(6)判断Pij中是否存在线特征。
2 含线特征的混合像元亚像元定位
首先利用模板匹配[22]的方法对混合像元Pij中呈线性分布的第c类地物进行亚像元定位。
以3×3模板为例,每个模板可用二进制矩阵表示为
(9)
式中,矩阵各元素t(m,n)∈{0,1},m,n=-1,0,1;k表示模板个数。同理,可以构建重建尺度为s的二进制模板矩阵。
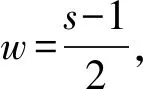
(10)
式中,Tk(m,n)表示第k个模板中元素t(m,n)的值;Sc表示图像中第c类地物的丰度值;ri,j,k为相关系数,值越接近1表示匹配效果越好,反之效果越差,因此,ri,j,k最大的模板为最佳模板。
最佳模板确定后,需要利用最佳模板Tk对混合像元Pij中第c类地物进行定位[22]。
首先根据丰度求得第c类地物在混合像元Pij内所占的亚像元个数Nc=Sc(i,j)×s2。为了便于计算,将混合像元Pij内二维表示的亚像元坐标及模板位置用一个统一的坐标系表示。如图3所示,以左上角为坐标原点,任意混合像元长度为1等于整个模板的长度,由此得到像元Pij内第p行q列亚像元Vpq坐标为
(11)
新坐标系中模板矩阵内元素t(m,n)的坐标为
(12)
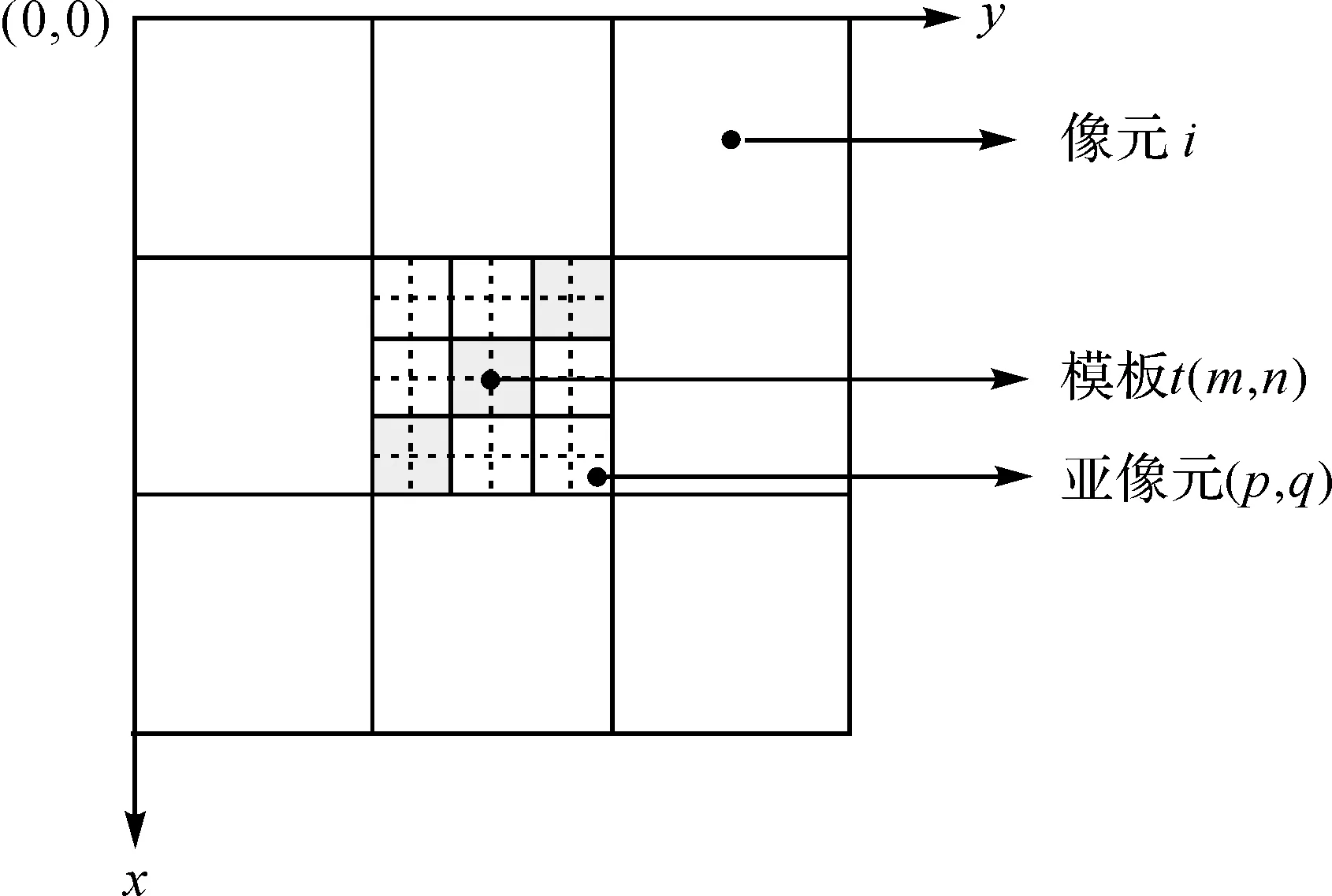
图3 模板/像元/亚像元同一坐标系统Fig.3 Unified coordinate system for template/pixel/subpixel
在统一坐标系中,计算亚像元vpq与最优模板Tk中各元素之间的欧氏距离
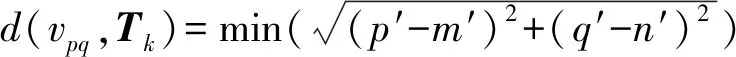
(13)
将所有亚像元到最优模板之间的距离进行升序排序,前Nc个亚像元类别为c,距离相等的情况下选择引力值大的亚像元进行定位。
如果混合像元Pij内仅含两种地物,则利用模板匹配方法[22]实现Pij中呈线性分布的第c类地物的亚像元定位后,Pij内的其他亚像元Pab类别可以直接确定。如果混合像元Pij内的地物类别大于两类,则根据像元引力确定其类别。采用环绕关系确定亚像元Pab的邻域像元集
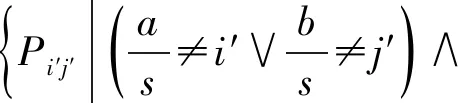
(14)
第c类地物对亚像元Pab的引力为
(15)
(16)
式中,maxcPab(c)为亚像元Pab的的类别。
3 面向线面地物分布的亚像元定位
线性优化的亚像元定位方法是将亚像元定位问题转化为线性优化问题,主要通过构造空间相关性的数学模型,其中空间相关性理论可以很好地实现面状地物的亚像元定位,但线状地物在定位时若采用空间相关性理论则会导致连通、细长的线状地物产生断裂,因此,本文采用分而治之的处理方式,将线状地物亚像元定位结合线性优化的面状地物亚像元定位,设计如图4所示的面向线面地物分布的亚像元定位算法框架。算法具体实现过程如下:
(1) 对高光谱图像进行光谱解混,并根据光谱解混的结果设置各像元的混合标志:纯像元标志为1,混合像元标志为0。同时,由高光谱图像的特点可以知道公路、小路、溪流等地物是明显具有线特征的,可以根据丰度分布图判断典型线状地物。
(2) 含线特征混合像元判定:对所有混合像元,按照以下两个步骤完成含线特征的混合像元判定:①所有含典型线状地物的混合像元都含线特征;②按照第1节的方法判断剩余混合像元中是否含线特征。
(3) 亚像元定位初始化:对于纯像元,直接确定其各亚像元的类别;对于混合像元,利用文献[7]的方法计算不同地物所占亚像元的个数,并初始化定位结果。
(4) 线状地物亚像元定位:按照模板匹配的方法实现混合像元内呈线状分布地物的亚像元定位,对于混合像元内其余地物则采用像元引力法进行定位。经线状地物亚像元定位后,更新初始化结果中含线状地物的混合像元的亚像元定位结果。
(5) 线性优化的亚像元定位:利用当前亚像元定位结果,对于不含线特征的混合像元,逐像元迭代优化,更新其亚像元定位结果。所用的逐像元迭代策略为[7]:每个像元每次迭代时,只计算其对应的亚像元窗及周围一圈构成的局部区域周长构造代价函数[6,20]
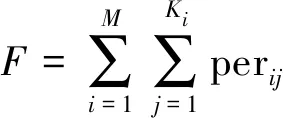
(17)
式中,M表示类别数;Ki表示第i类的连通区域个数;perij为第i类第j个连通区域的周长。迭代优化使目标函数式(17)最小。
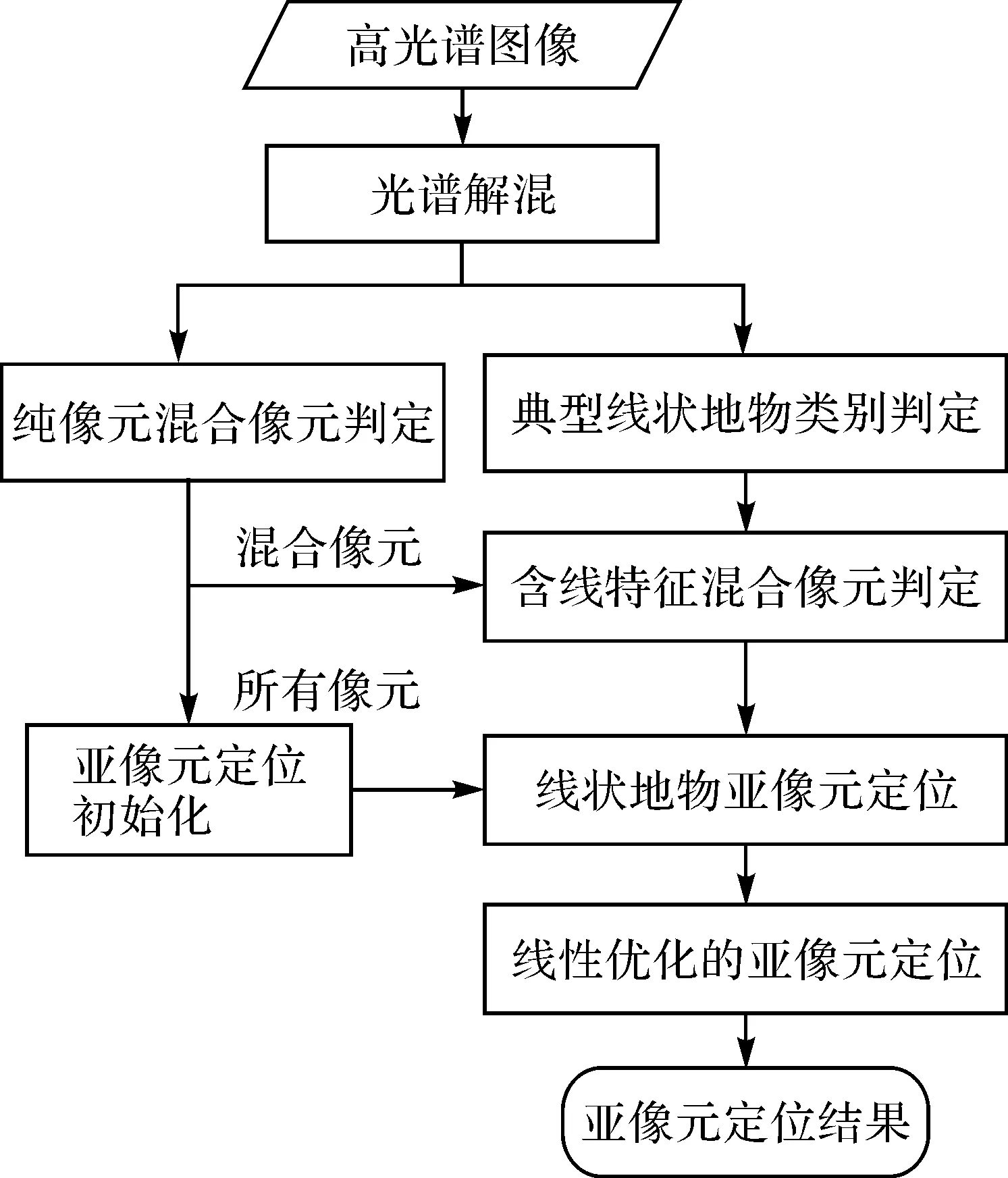
图4 面向线面地物分布的亚像元定位算法框架Fig.4 Subpixel mapping algorithm framework for areal and linear feature distribution
4 试验与分析
分别对提出的混合像元线特征探测方法和亚像元定位方法进行试验验证。所有试验中,通过文献[23]方法确定地物种类个数, 用主成分分析方法去噪,再用FNSGA方法[24]提取光谱曲线,全约束最小二乘法[25](fully constrained least squares,FCLS)求得丰度。试验环境为Intel(R) Core(TM) i5-3210M CPU,使用的MATLAB版本为MATLAB R2014a。
4.1 试验数据
4.1.1 仿真数据
从USGS光谱库中选图5(a)所示的7种地物光谱,按照图5(b)所示的地物分布,分别进行3×3比例和5×5比例均值滤波,构造相应的混合像元丰度,根据线性混合模型仿真,并加SNR=30的高斯白噪声,得到仿真的高光谱数据。图5(c)是大小为90×60仿真数据第40波段的灰度图,图5(d)是大小为54×36的仿真数据第40波段的灰度图。
4.1.2 真实图像
从高光谱数字图像收集试验(HYDICE)中获取的华盛顿购物中心高光谱数据,截取图6(b)所示的大小为240×240的子图,按3×3比例均值滤波缩小后得到图6(c)所示的80×80的图用于试验。该区域一共包含7类地物,分别为阴影、水体、道路、草地、树、房顶及小路,光谱曲线如图6(a)所示。
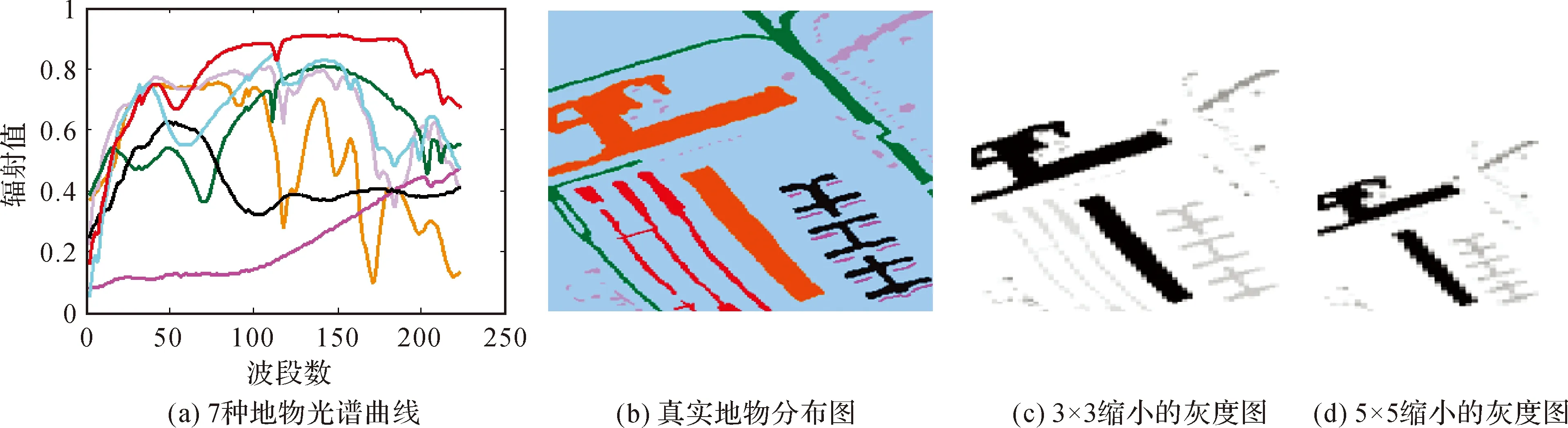
图5 仿真数据信息Fig.5 Simulation data information
4.2 混合像元线特征探测试验
首先进行混合像元线特征探测试验比较,选用方法为本文提出的基于完备直线集的最大线性指数法(CLS_MLI)、文献[21]的最大线性指数法(MLI)和文献[22]的形状密度指数法(SDI)。本部分试验的评价指标为ROC曲线(receiver operating characteristic)及运行时间。其中ROC曲线的横坐标为虚警率Pf,纵坐标为检测概率Pd,通过对横纵坐标数值统计实现对算法性能的量化分析。通常曲线越靠近左上角对应的算法性能越好,曲线下覆盖面积(area under curve,AUC)在0.5~1之间,数值越接近于1.0表明算法的线特征探测性能越好。当AUC取值为0.7~0.9时具有一定的准确性,在0.9以上具有较高的准确性[26],number代表含线特征的混合像元个数。另外对于含线特征的混合像元判断结果均采用灰度图显示,其中不同灰度代表不同地物类别。
图7给出了图5(c)所示仿真数据的线特征探测结果。其中,图7(a)表示图5(b)中绿色部分对应的典型线状地物,MLI法参数步进角度τ的取值分别为1和5。对照图5和图7进行分析,图7(b)中几乎将所有含线性特征的混合像元都判断出来了,包括面状地物中呈线性分布的边界,说明CLS_MLI法能够准确探测线性特征。图7(c)与图7(b)的线性混合像元判断结果基本一致,另外从图7(c)与7(d)的结果可以看出,随着旋转角度的增大,一些典型的线性特征被忽略,说明角度的选取将会影响混合像元线特征的判定结果。如图7(e)所示,SDI法只能将线性特征比较明显的混合像元判断出来,无法将地物边界呈线状分布的混合像元判断出来,说明SDI方法无法有效实现地物分布形状不太规则的高光谱图像线特征探测。

图7 仿真数据线性体判断结果Fig.7 Linear feature detection of simulation data
图8给出了仿真数据下不同线性体判断方法的ROC曲线,表1给出了相应指标的统计结果。如图8所示,MLI(τ=1)和CLS_MLI的ROC曲线相重合,这说明在本试验数据中MLI角度取为1时能取得较为准确的线特征探测结果,而CLS_MLI则不需要考虑步进角度大小对线特征判断结果的影响,且由图8和表1可以看出,MLI这种方法随着角度的增大,对于线性混合像元的判断效果越差。此外,SDI法与MLI(τ=5)时,两者的ROC曲线及曲线下面积相差不大,但由于SDI法不能实现亚像元级线特征探测,所以判断出的线性混合像元数量较少。
表1 不同方法线特征探测结果比较
Tab.1 Comparison for linear feature detection results of different methods

参数CLS_MLIMLI(τ=1)MLI(τ=5)SDInumber12051205444402AUC0.98650.98650.69510.7190
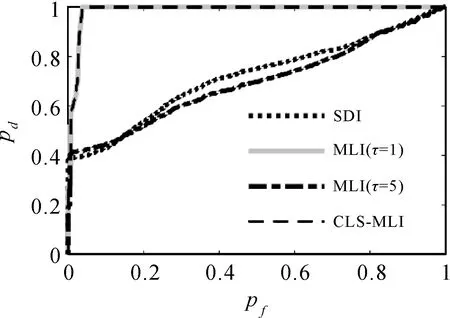
图8 线特征探测ROC曲线Fig.8 ROC Curve of linear feature detection
图9给出了图6真实图像线性体判断结果,对于含线性特征的不同地物采用灰度图显示,MLI法参数τ的取值仍为1和5。由于不同地物在高光谱图像中都有其特有的分布特性,如公路等具有连通细长的特点,森林、植被等具有大面积聚集的特点,因此可以根据不同地物在高光谱图像中的分布特性可以预先对线性特征进行判断,不仅可以增加辅助信息的利用也可以减少计算量。为此图9(a)给出了根据高光谱图像中地物特性预先判断出的线性体结果。如图9(b)所示,CLS_MLI法能够在图9(a)的基础上将地物边界上的线特征有效地判断出来,尤其是对于亚像元级的线特征判断。图9(c)—(d)在图9(a)的基础上,多了一些亚像元级的线特征,并且τ=1时,其结果接近于CLS_MLI;τ=5时很多明显的线特征没有判断出来。图9(e)中SDI方法在图9(a)的基础上增加了水体边缘线性体的判断,但无法准确判断亚像元级线特征如水体右侧道路中线及草地中的小路。

图9 真实数据线性体判断结果Fig.9 Linear feature detection of real data
表2分别给出了仿真数据和真实数据下不同线特征判断方法的时间比较。综合图7与图9的试验结果可以得出以下结论:① CLS_MLI能在较短的时间内将混合像元内是否存在线特征判断出来并且不用考虑角度因素的影响;② MLI在τ=1时结果接近CLS_MLI,但时间消耗比较大,随着角度的增大,时间消耗虽然会降低但判断出的线性特征会相应减少;③ SDI虽然运行时间比较快,但是线特征判断结果不如其他两种方法。由此可知,CLS_MLI效果最佳。
表2 线特征判断时间比较
Tab.2 Comparison of the CPU time for linear feature detections

项目CLS_MLIMLI(τ=1)MLI(τ=5)SDI仿真数据3.5232.246.851.19真实数据49.81455.0795.2735.71
本部分的试验结果表明,仿真及真实数据在MLI法的角度为1时能取得较好的线特征探测的效果,而CLS_MLI法不需要考虑步进角度对结果的影响,只需利用确定的直线就可以将线特征混合像元判断出来,且由表2可知CLS_MLI法判断线特征所耗费的时间少于MLI法。另外,CLS_MLI法对真实数据进行线特征判断时考虑了不同地物的高光谱特性,使得在线特征判断时减少了需要判断的混合像元的数量,提高了线特征判断的效率。
4.3 亚像元定位试验
为了验证本文提出的亚像元定位算法的性能,对所提出的基于线面地物分布的亚像元定位算法(SPM based on linear and area distribution,SPMLA)与不考虑线特征的线性优化亚像元定位算法(SPM based on linear optimization,SPMLO)进行试验比较。采用二进制粒子群算法为优化算法,目标函数采用基于缝隙的周长计算方法。根据4.2节的试验结果可知CLS_MLI方法线特征判断效果最佳,因此SPMLA的线特征探测采用CLS_MLI方法。另外为了验证模板匹配结合空间像元引力的方法优于仅使用模板匹配,分别对这两种线特征定位方法进行试验比较,为便于描述,分别记为SPMLA(TM+SAM)和SPMLA(TM)。由于粒子群算法的初值敏感性会影响结果,所以每组试验中各个算法每次运行全部使用同样的初始粒子群(粒子个数为30)。同时为有效验证亚像元定位的试验结果,本文以最后定位的识别率,Kappa系数及运行时间为客观指标评价算法性能,其中识别率表示为整个图像中像元正确分类的百分比含量。此方法是将待评估的分类图与参考图像中的像素点进行一一对应比较,通过计算得出最终结果。
4.3.1 仿真数据试验
对图5(c)进行亚像元定位的结果如图10所示,分别与图5(b)的真实分布对比。从图10(a)随机定位的结果中可以看出各地物边界区域断裂现象和毛刺现象非常明显,在SPMLO和SPMLA(TM)的定位结果中也存在少量边界出现毛刺及连通细长区域出现断裂的情况,并且从绿色和紫色区域分析,SPMLA(TM)结果比SPMLO略好一点。从图10中红色区域或红黑相间区域可以看出,图10(d)的SPMLA(TM+SAM)方法在地物边界的定位效果较好,定位出的地物边界比较光滑且连通性较好。这说明线面结合的亚像元定位方法优于传统的亚像元定位算法,也优于定位时仅考虑模板匹配的SPMLA(TM)方法。
对图5(d)进行5×5滤波后的亚像元定位如图11所示。与图10的定位结果相比较,图11无论从视觉效果还是地物连通性以及孤立点个数上定位效果都不是很好。由此可知随着重建尺度(S)的增大定位效果越不好,这是因为重建尺度的增大使得纯像元的个数减少,混合像元增多,从而定位效果降低。图11中给出的3种方法的结果已经很难分出哪种方法比较好。
表3给出了不同重建尺度下各算法的识别精度和运行时间比较,所有的结果都是运行5次取的平均值。从表3中可以看出,不同重建尺度下亚像元定位结果有所差异,总体上来说,重建尺度越大,定位效果越不好。通过分析可以得到以下结论:① SPMLA(TM+SAM)算法的识别率和Kappa系数均高于其他3种方法,定位效果相对较好,另外,由于在定位时结合了邻域像元引力,时间有所增加;② SPMLA(TM)的识别率及kappa系数均低于SPMLA(TM+SAM),这是因为SPMLA(TM)在模板匹配时未考虑邻域像元引力,也因为此原因使得其运行时间低于SPMLA(TM+SAM);③ 考虑线性体定位的定位算法的识别率和kappa值均高于没有考虑线性体定位的SPMLO方法。

表3 不同重建尺度下各亚像元定位结果比较
4.3.2 真实图像试验
对图6(c)进行亚像元定位。因为图6(b)的伪彩色图中含有大量的混合像元,滤波后的图像中纯像元变少,需要对图6(c)的丰度值做调整,将最大丰度值与其他丰度值之差的最小值大于0.5的像素作为纯像元。图12为对图6(c)进行3×3亚像元定位的结果。
从图12中可以看出,SPMLA(TM+SAM)法对明显具有线特征的地物定位时能够保持良好的连通性,而基于线性优化的方法在典型地物边界出现了很多断裂现象。另外,由于SPMLA(TM)算法在定位时仅考虑了混合像元内具有线特征地物的定位,使其定位效果不如SPMLA(TM+SAM),但由于该区域的地物分布比较复杂,所以定位效果从视觉上无法直接给出更好的判断。为了更好地说明上述试验,截取图13(a)所示的长方形区域对应的3×3亚像元定位结果进行放大分析,结果如图13(b)—(d)所示。
从图13(b)可以看出SPMLO由于不进行线性体判断及定位的处理,所以定位的结果虽然能够还原小路的形状但是连通性不如其他两种方法,小路产生了明显的断裂。而SPMLA(TM+SAM)和SPMLA(TM)的结果较好,小路整体比较平滑,这是因为这两种算法根据高光谱特性将小路直接判断为线状地物。比较分析图13(c)和13(d),可以看出SPMLA(TM+SAM)的效果稍微好一些,这是因为SPMLA(TM)法对混合像元内具有线性特征的地物定位完成后,对剩余地物的定位时未考虑空间引力。
5 结 论
为了提高高光谱图像亚像元定位精度,提出基于混合像元线特征判定的亚像元定位方法。本文所提出的基于完备直线集的线特征判断方法,通过预先判断混合像元内肯定不可能呈线性分布的地物类型,提高了算法效率;通过完备直线集的直接构造,避免了步进角度的选取对线特征判断结果的影响。所提出的模板匹配结合像元引力的含线特征混合像元亚像元定位方法,在对混合像元内线特征地物定位完成后的其余地物定位时加入像元引力,试验结果表明该方法可以有效提高定位精度。所提出的线面结合的亚像元定位框架,不仅考虑了线状地物的亚像元定位也考虑了面状地物的亚像元定位,从而整体上提高了亚像元定位精度。
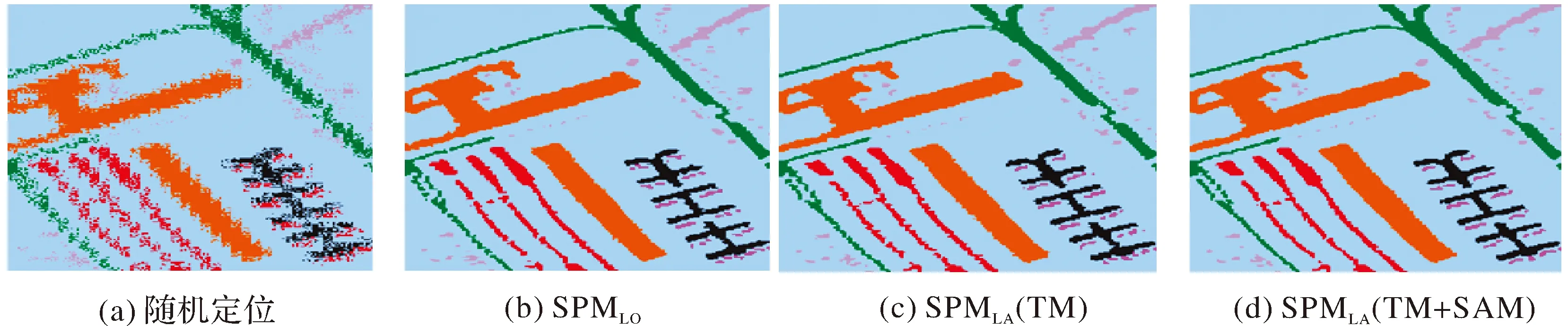
图10 图5(c)对应的3×3亚像元定位结果Fig.10 The 3×3 subpixel mapping results in Fig5(c)
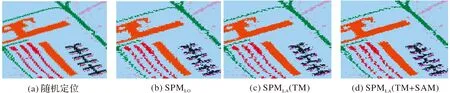
图11 图5(d)对应的5×5亚像元定位结果Fig.11 The 5×5 subpixel mapping results in Fig5(d)
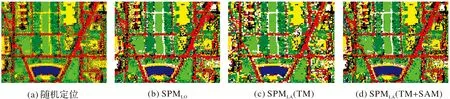
图12 图6(c)对应的3×3亚像元定位结果Fig.12 The 3×3 subpixel mapping results in Fig6(c)
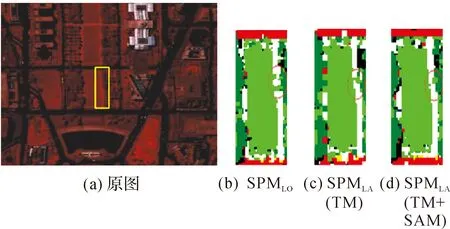
图13 截取部分区域放大后的亚像元定位结果Fig.13 Intercepting the sub-pixel mapping results of the enlarged area
由于在模板匹配时本文采用的方法为标准相关匹配,求得的最佳模板可能会有多个,本文目前尚未解决多个模板中如何智能选取最优模板的问题,只能根据模板出现的先后顺序进行选取,这也是下一步的研究内容,从而进一步提高亚像元定位精度。
