基于IOWA的在线英语教学学习人数组合预测模型
2019-11-19赵洋
赵洋
(西安交通大学 城市学院, 西安 710049)
0 引言
改革开放以来,高等教育得到长足的发展,英语在线网络教学和学习系统在各大高校得到了广泛应用,在管理、学习、评价和监控系统的应用过程中,形成了大量有价值的信息数据,包括学生个人信息、在线学习人数、课程考试成绩、学习时长、学习兴趣点、作业完成情况、学习过程评价等[1]。然而目前这些有价值的数据并未发挥其真实的作用,若能够利用相关学习分析技术和数据挖掘方法发掘出潜在的有价值的规律,有助于英语网络学习流程和管理流程的优化设计,同时可以为英语网络教学提供科学决策的依据。
随着在线学习英语人数的大量增加,如何实现英语在线学习人数的准确预测,对网络教学资源的合理配置和利用具有十分重要的意义。针对英语教学在线学习人数单一预测模型存在预测精度低和误差大的缺点,在支持向量机、指数平滑和BP神经网络模型的基础上,提出一种基于IOWA算子的在线英语教学学习人数预测的组合模型。
1 在线英语教学学习人数预测模型
1.1 支持向量机

s.t.yi[(W·Xi)+b]-1≥0(i=1,2,…,n)
(1)
其中,b表示偏置,W表示平面间隔。公式(1)描述的问题可转化成偶化问题为式(2)。
s.t.αi≥0(i=1,2,…,n)
(2)
其中,αi表示Lagrange算子。公式(2)的矩阵表示形式如式(3)。
s.t.αi≥0(i=1,2,…,n)
yTα=0
(3)
式中,α=(α1,α2,…,αn)T,b=(1,1,…,1)T,y=(y1,y2,…,yn),Aij=yiyj(xi·xj)。
最终,SVM的决策函数可表示为式(4)。
(4)
1.2 指数平滑法
若英语在线学习人数时间序列为{x1,x2,…,xN},则一次指数平滑(Exponential Smoothing,ES)的递推数学模型如式(5)[3]。
(5)

1.3 BP神经网络
BP神经网络是一种误差反向传播的网络,其结构模型如图1所示[4-5]。

图1 BP网络结构图
针对英语在线学习人数时间序列{y1,y2,…,yN},其预测流程如下:
(1)假设BP神经网络的在线学习人数预测模型的输入为Y1={y1,y2,…,yD},Y2={y2,y3,…,yD+1},…,Yk={yk,yk+1,…,yD+k},在线学习人数预测模型模型对应的输出为z1=yD+1,z2=yD+2,…,zk=yD+k+1。
(3)将Y1,Y2,…,Yk作为BP神经网络在线学习人数预测模型的输入,对应在线学习人数的预测输出数据为z1,z2,…,zk,建立预测网络并进行训练,训练之后的网络模型为式(6)。
zi=f(Yi)
(6)
为了加速网络的收敛速度和提高预测精度,对数据进行归一化预处理,归一化式如式(7)[12]。
(7)
其中,xmin、xmax分别表示英语在线学习人数时间序列{y1,y2,…,yN}中的最小值和最大值。
(4)建立模型后,进行单步预测如式(8)、式(9)。
(8)
(9)

(5)重复(2)-(4),就可以实现英语在线学习人数的预测。
2 IOWA组合预测模型
OWA算子是对n个数x1,x2,…,xi,…,xn递减排序之后进行赋权平均的,其中权值系数ωi只与xi所在的位置i有关。IOWA算子是在OWA算子的基础上将一元函数扩展成为二维数组,若〈z1,x1〉,〈z2,x2〉,…,〈zn,xn〉表示n个二维数组,令式(10)。
(10)

假设英语在线学习人数时间序列为{xt,t=1,2,…,N},假设有m种可行的单项预测方法可以实现在线学习人数预测。若xit表示第i种模型在第t时刻的预测值,其中i=1,2,…,m。
当|(x1-xit)/xt|<1时,ait=1-|(x1-xit)/xt|;当|(x1-xit)/xt|≥1时,ait=0。ait表示第i种模型在第t时刻的预测精度,其中ait∈[0,1],ait表示xit的诱导值。第t时刻,研究对象的预测精度和预测值组成〈v1t,a1t〉,〈v2t,a2t〉,…,〈vnt,ant〉二维数组,设W=(ω1,ω2,…,ωm)T表示m种预测模型在组合预测模型中所占的权重系数,将第m种模型在第t时刻的预测精度序列a1t,a2t,…,amt按照降序排列。设a-index(it)表示第t时刻第i个大的预测精度的下标,则式(11)。
(11)
令ea-index(it)=xt-xa-index(it),因此N期的组合预测误差平方和S可表示为式(12)[7-8]。
(12)
因此,基于IOWA算子的新型组合预测模型可表示为式(13)。
(13)
ωi≥0,i=1,2,…,m

minS(W)=WTEW
s.t.RTW=1
W≥0
(14)
其中,R=(1,1,…,1)T,W=(ω1,ω2,…,ωm)T。
3 实证分析
3.1 数据来源
为了验证本文算法的有效性和可行性,选择我国2002年~2017年英语教学在线学习人数为研究对象,数据如表1所示。

表1 英语教学在线学习人数
分别研究SVM[9]、指数平滑[10]、BP神经网络[11]和IOWA组合模型的英语教学在线学习人数预测。将2002年~2015年数据作为训练数据,用于建立预测模型,建立模型之后对2016年~2020年英语教学在线学习人数进行预测。
3.2 评价指标
为了评价预测模型的效果,选择平均绝对误差(Mean Absolute Error,MAE)和平均相对误差(Mean Relative Error,MRE)作为预测模型精确度的评价指标,二者分别为式(15)、式(16)。
(15)
(16)

3.3 实证分析
针对我国2002年~2015年英语教学在线学习人数时间序列,分别研究SVM、指数平滑、BP神经网络和IOWA组合模型的英语教学在线学习人数预测,其预测结果如图2~图5所示。

图2 BP、ES、SVM和IOWA预测结果对比图

图3 BP、ES、SVM和IOWA预测绝对误差对比图

图4 BP、ES、SVM和IOWA预测相对误差对比图
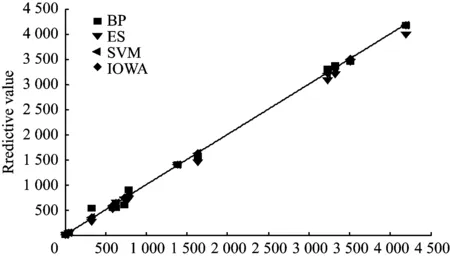
图5 BP、ES、SVM和IOWA预测相关性
由图2~5英语教学在线学习人数预测结果可知,组合预测模型的精确度相对于单一预测模型而言,有很明显地优越性,经过计算可知,组合预测模型的精度高达96.67%。
为更清晰地反映基于IOWA算子的组合预测模型和其他单一预测模型的预测误差,不同方法的预测指标对比结果如表2所示。

表2 不同方法预测结果评价指标对比
由表2可知,基于IOWA算子的组合预测模型的两个评价指标均明显低于其他三个单一预测模型,由此证明本文提出的基于IOWA算子的组合预测模型可有效提高预测精度。
对2016年~2020年英语教学在线学习人数进行预测,预测结果如表3和图6所示。

表3 2016~2020年英语教学在线学习人数

图6 预测结果
由表3和图6可知,IWO组合预测模型在2016年和2017的预测结果分别为3 708.17和4 164.25,与实际值的绝对误差的绝对值分别为37.46和109.91,相对误差分别为1.00%和2.71%,效果较好。
4 总结
选择我国2002年~2017年英语教学在线学习人数为研究对象,在SVM、指数平滑、BP神经网络等三种单项预测模型的基础上,提出一种基于IOWA算子的英语在线学习人数组合预测模型。实证分析结果表明,该方法可以有效提高预测的精度。但是,需要引起注意的是,影响预测结果的调节系数很多,如学习目标、留学政策、学习兴趣、地区差异等。因此,后期需要在本文的研究基础之上,进一步考虑相关影响因素,找到影响英语在线学习人数的核心因素并对其进行量化处理,进一步完善在线学习人数预测模型。
