汽车衡安装误差对称重精度的影响分析
2019-11-16赖朝晖杨晓翔姚进辉赖征创
赖朝晖 杨晓翔 姚进辉 赖征创


摘要:利用准静态分析方法研究偏载对汽车衡称重精度的影响,偏载越严重,称重值越小,误差越大。柱式负荷传感器安装的初始倾斜造成传感器偏斜承载,由力的平衡关系求得的各传感器偏斜角度之和随荷载移动保持不变。由材料力学公式计算秤台随荷载移动的变形量,表明作用在秤台上的荷载越大,上压头和传感器偏载越大。秤台倾斜安装角度超过临界角度时,利用静力学平衡原理得到倾斜角度越大,弹性体高度越大,球头半径越小,偏载越大。通过有限元软件分析柱式负荷传感器安装标高误差对各传感器支承点上压头转角随荷载移动的变化过程,结果表明标高差越大,各支承点上压头转动角度变化幅度越大,偏载越严重。当标高差过大时将处于三点支承状态,减小秤台承载刚度,秤台变形增大。最后,给出可提高秤台刚度和控制偏载的相关措施。
关键词:动态汽车衡;误差分析;准静态分析;误差控制;动态称重
中图分类号:TH823 文献标志码:A 文章编号:1674-5124(2019)07-0108-09
收稿日期:2018-06-20;收到修改稿日期:2018-08-01
基金项目:国家重大科学仪器设备开发专项(2011YQ090009)
作者简介:赖朝晖(1989-),男,福建龙岩市人,硕士研究生,专业方向为动态称重系统的开发。
通信作者:杨晓翔(1963-),男,内蒙古赤峰市人,教授,博士生导师,研究方向为计算力学及其工程应用。
0 引言
轴组式动态汽车衡因成本较低、称重精度较高,在高速公路收费站的动态称重系统中应用较广。轴组式动态汽车衡由4个柱式负荷传感器和其支承秤台组成[1]。柱式负荷传感器放置于称重秤台和地基基础之间,起着承载和称重的作用[2]。动态汽车衡在称量过程中的精度影响因素历来是研究的热点问题,包括路面、车辆、信号传输与处理等方面,同时提出改善对策[3-5]。冯秀丽等[6]对随机路面与汽车动荷载进行了理论分析与计算机仿真,研究了路面不平度、汽车行驶速度对动态称重结果的影响,为进一步提高汽车衡动态称重的精度提供了理论依据。李斌[7]研究了速度与加速度对动态称重系统的影响,将汽车振动模型进行简化,在给定路况下不同速度的动荷载进行仿真,得到不同速度和加速度对称重精度影响的一般规律。李莹[8]分析了动态汽车衡称重存在的技术问题、组成部分及工作原理,归纳了几类误差影响机制,并对动态汽车衡的检定方法提出了相关建议。
在汽车衡安装施工过程中,由于各种原因,不可避免地存在着各种误差,如柱式负荷传感器安装的初始倾斜,秤台受载变形影响,秤台倾斜安装及柱式负荷传感器安装的标高误差等。这些安装施工误差将导致柱式负荷传感器产生摆动,承载压头产生倾斜,重力作用线不再沿柱式负荷传感器的轴线方向,从而影响柱式负荷传感器的工作特性和称重精度。在柱式负荷传感器受偏载误差分析方面,陈俊翔等[9]对偏离轴线的荷载产生附加弯矩和侧向力等寄生分量进行了实验研究,得出附加弯矩是传感器方位误差产生的重要原因。Peters M等[10-11]在做了大量的比对试验后发现,力的非轴向分量及附加弯矩是造成方位误差的直接原因。
本文以由摆动支承柱式负荷传感器支承的轴组式动态汽车衡为研究对象,在动态称重条件下,将称重系统的称重过程视为准静态过程,分别对各安装施工误差产生原因和其称重过程进行受力分析,得出其对柱式负荷传感器称重准确度的影响大小和主要影响因素,为动态汽车衡的误差分析和维护保养提供理论依据,并给出了相关的控制措施以提高称重稳定性和准确度。
1 柱式负荷传感器摆动支承误差分析
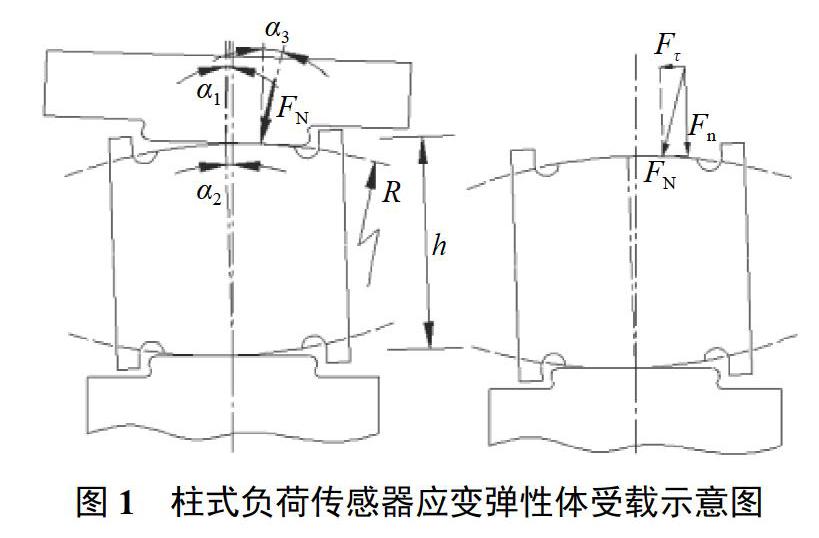
摆动支承柱式负荷传感器由中间部位的应变弹性体和上下压头组成。取C16A C3型20t圆柱式双球面弹性体的柱式负荷传感器为承载器,这种装置能够自动定心承力传力,并起到限位的作用,其结构受载简图如图1所示[12]。
设传感器逆时针转角为a2,处于稳定平衡的摆动支承状态时,传感器在与上压头的接触点所受的外力FN可分解为沿应变弹性体轴线的轴向力Fn和切向力Fτ[13],分别为
Fn=FNcos(α1+α2+α3)
Fτ=FNsin(α1+α2+α3)(2)式中:α1——士压头倾角,rad;
α2——傳感器应变弹性体轴线倾角,rad;
α3——外力方向与上压头轴线的夹角,rad。
根据拉压弹性元件的全桥接法,理论上传感器的输出应变值只跟沿着弹性体轴线应变方向的轴向力大小有关,而与切向力和切向力所产生的附加弯矩无关[14]。测量的相对误差为
2 安装施工误差影响分析
2.1 柱式负荷传感器倾斜安装对称重的影响
选取四点支承的轴组式动态汽车衡为研究对象,当支承的各传感器发生不同方向的转角时,秤台对传感器有水平方向的摩擦力,如图2所示。传感器应变弹性体在上下压头间纯滚动,以弹性体不偏转时的接触点为参考点,当弹性体偏转α21角度时,上压头的水平位移为
S21=2Rα21-(2R-h)sinα21(4)式中:h——传感器应变弹性体沿轴线的高度,mm;
α21——传感器应变弹性体轴线的安装倾角,rad;
R——球头半径,mm。
同时,有几何关系式[14]
OH=(2R-h)sinα21(5)
HK=2R-(2R-h)cosα21(6)
设左侧两个传感器安装倾角相等,右侧两个传感器也相等。当弹性体偏角较小时,滚动摩阻小于最大滚动摩阻力偶,秤台不产生平动,因而秤台对弹性体的摩擦力为零。当弹性体倾角大于临界角度时,秤台在回复力作用下有平动的运动趋势,秤台对弹性体产生摩擦力。设施加荷载前,转角分别为α01和α02,施加荷载后状态如图2所示。
以图中所示受力方向为正方向,由弹性体对支承点O的力矩平衡关系,有其中,Mfl=δ0FN1,Wf2=δ0FN2,δ0为弹性体与上下压头间的滚阻系数。FN1=0.25Mg+0.5F(l-a)/l,FN2=0.25Mg+0.5Fall,小角度时,cos α21=cos α22≈1。弹性体偏转引起左、右上压头的水平位移大小相等,有
S21-S01=-(S22-S02)(10)其中,S01和S02为初始安装时传感器偏转引起参考点的水平位移。
当初始安装倾角满足(R-0.5h)sinα01≤δ0,(R-0.5h)sinα02≤δ0时,弹性体所受力矩不足以克服滚动摩阻力偶,秤台不产生摩擦力。
当一侧传感器倾角大于临界角度时,弹性体有滚动趋势,秤台产生水平摩擦力,两侧弹性体的滚动摩阻力偶大小和方向取决于滚动趋势。设右侧弹性体倾角满足(R-0.5h)sinα02>δ0,持续增加荷载,使两侧弹性体滚动摩阻均达到最大滚动摩阻力偶,当所受力矩大于最大滚动摩阻力偶时,弹性体将向左转动,直到形成新的平衡状态,此时两侧弹性体的滚动摩阻等于最大滚动摩阻力偶,由式(7)~式(9)得
根据式(10),有
联立式(12)、(13)可得摆动后的倾角α21,α22。
当初始安装倾角满足(R-0.5h)sinα01>δ0,(R-0.5h)sinα02>60时,秤台对弹性体始终有摩擦力,通过对图2左右两侧弹性体单独计算其合力矩,合力矩大的一侧有使系统往该侧正方向转动的趋势。当两侧弹性体在一个方向上所受力矩都大于最大滚动摩阻力偶时,若弹性体均往左滚动时,计算过程同式(11)~式(13)。
取表1所示参数,按照以上推论,可以求得秤体产生摩擦力的临界角度为9.1×10-4rad。在安装时存在初始倾角的情形下,左、右两侧传感器弹性体的转角α21、α22变化情况,如图3所示。
由图中曲线可知,弹性体转角与其受载前各自的倾角无关,而与其倾角之和的大小有关,在受载过程中,倾角之和保持不变。在传感器弹性体产生上述转角时,由式(3)可得各传感器称重结果的相对误差大小。受载结束后,弹性体倾角不会恢复受载前的状态,并影响后续的称重。此外,摩擦力的存在也减小了称重数值。
2.2 秤台受载变形对称重的影响
秤台刚度较小,而外载较大时,秤台将产生过大的变形,这种变形使支承点的弹性体发生角位移,影响称重准确度,如图4所示。当秤台施加荷载时,由于秤台变形,两侧弹性体接触点之间的距离发生变化,两侧弹性体将向相反的方向偏转。转动达到平衡时,弹性体接触点达到最大滚动摩阻力偶,如图5所示。根据秤台受载变形过程可知,当0 同理,由弹性体对支点O的力矩平衡关系,有 F1[(2R-h)sinα21+Rsinα11]-2Mf1-FS1h=0(14) F2[(2R-h)sinα22+Rsinα12]-2Mf2-FS2h=0(15) 秤臺中性层变形曲线近似为直线,原支承点截面中性轴位置水平距离缩小S1+S2,根据初始接触点的位移关系,得到补充方程 2R(α21+α22)-(2R-h)(sinα21+sinα22)=(h2+h3)tsinα11+sinα12)-(S1+S2) 由式(9)、式(14)~(16)可求得弹性体角度与荷载大小和位置间的关系。 将秤台视为两边支承的简支梁[15],忽略秤台的初始变形和弹性体的滚动摩阻力偶,由材料力学公式有 θ=arcsinδ/x(21) S1=x(1-cosθ)(22) S2=(l-x)(1-cosθ)(23)式中:δ——秤台的最大挠度,mm;
EI——秤台梁的弯曲刚度,N·mm2;
l——秤台支承长度,mm;
a——荷载至左端支承点水平距离,mm;
x——δ所在位置至左端支承点水平距离,mm;
S1——左侧支承点截面处中性层的水位移,mm;
S2——右侧支承点截面处中胜层的水平位移,mm。
为研究秤体变形对称重精度的具体影响,选取如表2所示的轴组式动态汽车衡模型参数,得到单轴载在秤台上移动时,不同位置处左侧上压头倾角和应变弹性体倾角的变化情况,如图6和图7所示。从图6可以看出,荷载开始远离支承端时,上压头倾角增大,临近中点时缓慢减小,过中点后迅速减小至零。从图7可以看出,荷载开始远离支承端时,支承端的弹性体先向右侧偏转很小的角度,然后再往左侧偏转,其极值点在过中点的另一侧,然后减小至零。同时荷载越大,上压头倾角和传感器弹性体向外的转角也越大。由材料力学公式可知,秤台刚度和支承点离中性轴的竖向距离影响弹性体转动的转向和大小。在传感器弹性体产生上述转角时,由式(3)可得各传感器称重结果的相对误差大小。此外,摩擦力的存在也减小了称重数值。
2.3 秤台倾斜安装对称重的影响
早期高速公路收费站的计重系统多为轴重式动态汽车衡,轴组式动态汽车衡因精度高、造价较低,最近几年得到推广。因此,高速公路收费站的称重系统多由轴重衡改装为轴组式动态汽车衡。为顺应地形,排出雨水的考虑,秤台安装时采用倾斜安装的形式,如图8所示。
在秤台倾斜安装的情形下,秤台对柱式负荷传感器的重力将偏离应变弹性体轴线方向。因应变弹性体与上、下压头间存在滚动摩阻,应变弹性体将随着秤台倾斜角度的增大由静止状态变为滚动状态,如图9所示。
取一个柱式负荷传感器为研究对象,受秤台1/4重力的作用。当倾斜角度较小时,传感器弹性体不发生摆动,设临界角为θ1,滚动摩阻系数δ0=0.05mm,由弹性体摆动支承平衡,有
得临界角
竖向重力的力矩大于最大滚动摩阻时,弹性体发生摆动,设平衡时,摆动角度为α,由力矩平衡关系,有
得摆动角度与斜坡坡度间的关系式
当秤台倾斜角度超过临界角时,秤台对传感器重力的力矩超过弹性体最大滚动摩阻,弹性体产生倾角,应变弹性体倾斜角度与秤台倾斜角度的关系如图10所示。从图中可知,二者近似成线性关系,在相同秤台倾斜角度下,弹性体高度越大,球头半径越小,弹性体倾斜角度越大。在传感器弹性体产生上述转角时,由式(3)可得传感器称重结果的相对误差大小。
2.4 柱式负荷传感器安装标高差对称重的影响
由于基础施工预埋钢垫板存在标高误差,后期基础沉降,及秤台受载后不可恢复的变形等影响,导致秤台的4个支承点标高不一致,影响称重准确度。秤体在空间中有6个自由度,如图11(a)所示,秤台可由任3个柱式负荷传感器支承。设支承点4标高差为δ4,秤台重心在支承点2一侧,支承点1限制3个平动自由度,支承点3限制2个转动自由度,另外,支承点2限制1个转动自由度,是单侧约束,不计柱式负荷传感器的弹性变形,约束条件为
当y2=0,δ4+y4>0时,此时秤台由三点支承,由平衡方程
F1+F2+F3=FG
FGb=F2c
F3l2-FGz=0
得各支承点的支承反力为
且有
当y2=0,δ4+y4=0时,秤台由四点支承,如图11(b)所示,可视为一次超静定结构,由平衡方程
F1+F2+F3+F4-FG=0
(F3+F4)l2-FGz=0(32)
(F2+F3)l1-FGd=0
协调方程
δ4+y4=0(33)
可求得各支承点支承反力的大小。
当y2>0,δ4+y4>0时,秤体将绕φ轴旋转,直到由传感器4施加单侧约束,外载FG近似在秤台中心,转动过程很短暂,不计惯性力,这时,各传感器受力为
F2=F4=0
F1=F2=1/2FG(34)
F1=F3=1/2FG
当y2>0,δ4+y4=0时,传感器4限制转动自由度,同理为单侧约束,受力状态与y2=0,δ4+y4>0时的情形相同,为三点支承。
因传感器承载點的高差,会导致秤台受载变形的增大,尤其是三点支承的状态,降低了秤台承载刚度,秤台变形程度高于四点支承状态。秤台变形过大,传感器受载波动较大,将影响传感器垂直受力特性和数据输出的稳定性,影响测量精度。
考虑U形梁结构秤体,采用有限元软件分析秤体4个支承点在称重过程中称重准确度受支承点标高差的影响。取两轮单轴荷载为秤台所受外载,分析前轴驶过秤台中间U形梁段的过程中,各传感器支承点在支承点4存在标高误差δ4下的支承反力的变化情况。设单轴载FG=50kN,两轮接地面积A=430cm2,则接地压力P=1.08MPa。取U形梁一端为荷载位置起始点,分析不同支承点标高差下,各支承点上压头纵向倾角随轴载在不同位置的变化过程,如图12所示。图12(d)可以看出,全程3点支承和全程由3点过渡到4点支承两种情形间的临界标高差约为δ4=3.8mm。
从图12(b)、图12(c)可知,支承点2和4在受载阶段上压头倾角差异不大,支承点1的上压头倾角随标高差的增加而增大,支承点3的上压头倾角在受载的前半程随标高差的增大而增大,而在处于三点支承状态的后半程阶段,倾角迅速减小,但此时应考虑标高差造成传感器3和4上压头横向承载面的倾斜,倾斜角度为
由此可见,支承点3的上压头倾角在3点支承状态的后半程阶段的减小并不能降低称重误差,因秤台在支承点3和4的横向倾斜反而使误差随标高差的增加而增大。在传感器弹性体产生上述转角时,由式(3)可得各传感器称重结果的相对误差大小。
3 安装施工误差控制措施
3.1 传感器安装施工误差控制
柱式负荷传感器在秤台受载后,会产生倾斜,致使重力偏移应变弹性体轴线,导致测量出现误差,应加强检测,控制弹性体初始倾斜量。对于弹性体随秤台变形发生转动的情况,根据实际经验,型号为C16A C3的柱式负荷传感器操作手册给出了如下措施:当负荷传感器偏斜较大时,可以在传感器上、下压头塞入垫片来调节应变弹性体的偏斜量,如图13(a)所示,或者如图13(b)在初始安装负荷传感器时,可以让应变弹性体稍微内倾以抵消秤台的弯曲变形对上压头外推位移影响,也可以将上压头顶部安装在中性层位置以消除此影响,如图13(c)所示。
3.2 秤台安装施工误差控制
为控制秤台受载弯曲变形对柱式负荷传感器称重精度的影响,应适当提高秤台的弯曲刚度,如对秤台表面预拱,用钢结构的预应力处理法提高秤台的刚度等[16]。同时,应控制秤台安装的倾斜角度,或在压头与秤台连接处塞入垫片使压头处于水平状态,避免弹性体在偏斜受载下发生倾斜。
3.3 柱式负荷传感器支承点标高误差控制
施工时,加强地基处理以减少地基沉降,同时应严格控制柱式负荷传感器放置处预埋钢板的标高误差,保证秤台各支承点尽可能处于同一标高处。日常维护保养时,应观察测量各支承点的标高差,当超出一定范围时,可在传感器底座塞入垫片来调整支承点的标高,减小称重误差。
4 结束语
轴组式动态汽车衡的称重精度研究以往比较侧重于从秤台本身、车辆、路面和称重数据处理方面进行分析,而对安装施工因素的研究较少。本文研究了安装施工误差对测量准确度的影响,并提出了相应的处理措施。得出的主要结论和措施有:
1)轴组式动态汽车衡测量精度的影响因素是应变弹性体的倾角、上压头的倾角,反映为被测荷载沿弹性体轴线的力分量为测量输出量。
2)影响应变弹性体倾斜的因素有应变弹性体初始安装的倾角,上压头水平位移带动应变弹性体的滚动而产生倾斜。应在日常维护时加以检查及时调整应变弹性体倾斜,也可以将弹性体稍微内倾以抵消上压头的带动作用。
3)秤台弯曲变形使上压头产生转角和位移,导致荷载作用方向改变和应变弹性体的滚动倾斜,可以加强秤台弯曲刚度或在上下压头塞入垫片抵消端部截面倾角的影响,也可以将上压头顶部安装在中性层上以消除此影响。
4)秤台各支承点存在标高差时,将增大支承点的纵向转动角度,使称重误差增大。在标高差过大时,称重过程全程处于三点支承状态,秤台弯曲刚度小,同时秤台的翻转将加剧称重系统的不稳定性。应加强地基处理减少沉降或塞入垫片调整标高的方式控制各支承點的标高差。
参考文献
[1]朱国伟,范长江,周骥,等.浅谈动态汽车衡发展史[J].中国交通信息化2016(7):98-99.
[2]王琪.基于专家系统的轴组式动态称重仪表的研究与设计[D].太原:太原理工大学,2017.
[3]周祖濂.车辆动态称重[C]//第三届全国称重技术研讨会,2001.
[4]王祯荣.动态电子汽车衡计量准确度影响因素及对策[J].衡器,2001,30(5):33-36.
[5]郭京生,杨丽华,杨家润,等.影响动态汽车衡测量精度因素及采取的措施[J].仪器仪表用户,2007,14(1):115-117.
[6]冯秀丽,李晓林,杨洪扣.路面不平度与汽车速度对动态汽车衡称重的影响[J].中国科技论文,2012,7(11):857-861.
[7]李斌.速度与加速度对动态称重系统的影响[J].山西电子技术,2015(1):43-45.
[8]李莹.动态汽车衡称量误差影响分析及检定方法的研究[D].太原:太原理工大学,2012.
[9]陈俊翔,梁伟,杨晓翔,等.球头接触副对柱式负荷传感器方位误差的影响研究[J].机电工程,2018,35(4):341-346.
[10]PETERS M.Limits to the uncertainty achievable in forcetransfer[J].Measurement,1984,2(4):197-202.
[11]FERRERO C.The measurement of parasitic components innational force standard machines[J].Measurement,1990,8(2):66-76.
[12]刘九卿.电子汽车衡承载器承力传力定位限位结构分析[C]//第十四届称重技术研讨会,2015.
[13]颉锋锐,吝晓龙,蔡文强,等.柱式传感器与桥式传感器在汽车衡中的应用性能分析[J].中国交通信息化2017(7):139-141.
[14]林鸿志,吴建伟,杨莉,等.柱式传感器倾斜误差问题初探[J].衡器,2016(1):36-38.
[15]王祯荣.浅谈电子汽车衡秤台结构与刚度计算[J].衡器,1997(1):24-26.
[16]韦铁平,杨晓翔,许艺青,等.基于预应力处理法汽车衡秤体刚度研究[J].机械强度,2017,39(6):1485-1489.
(编辑:商丹丹)
