某重型变速器壳体的动态特性分析
2019-11-16任波杨啟梁胡溧
任波 杨啟梁 胡溧


摘要:为分析某重型变速器壳体的动态特性,基于LMS Test.Lab软件,使用激振器法进行试验模态分析,基于Hypermesh软件,使用Block Lanczos法进行计算模态分析。分析结果表明,橡胶轮胎支撑可模拟该自由模态试验的边界条件;变速器壳体主副箱连接方式为面面接触及采用高阶四面体单元可以获取更准确的计算模态参数;两种方法获取的壳体非零前六阶固有频率相对误差皆小于5%,振型基本一致,验证该壳体有限元模型的准确性。此研究表明结构模态分析技术对结构动态特性分析的有效性,为分析及改善该变速器总成的动态特性奠定基础,为类似结构的重型变速器壳体模态分析提供参考。
关键词:重型变速器壳体;动态特性;试验模态分析;计算模态分析;模态参数
中图分类号:U467.3 文献标志码:A 文章编号:1674-5124(2019)07-0051-05
收稿日期:2018-04-06;收到修改稿日期:2018-05-10
作者简介:任波(1993-),男,湖北十堰市人,硕士研究生,专业方向为汽车动力学与汽车NVH(噪声、振动与声振粗糙度)。
通信作者:杨傲梁(1962-),男,湖北武汉市人,教授,研究方向为汽车NVH。
0 引言
研究结构动态特性最常用的方法是结构模态分析技术[1]。结构模态分析技术分为计算模态分析和试验模态分析[2-3]。计算模态分析主要基于有限元软件来获取结构模态参数,如Workbench[4]、Abaqus[5]软件。试验模态分析是通过激励被测对象同时采集激励和响应信号进行参数识别得到结构模态参数。锤击法(SISO)为试验模态分析中较常用的方法。H.Nahvi等[6]、向玲等[7]利用锤击法提取了悬臂梁的模态频率和振型;吕孟理[8]等采用锤击法对某轻型变速器壳体进行了自由模态测试。随着振动理论、传感器技术及信号处理分析技术的飞速发展,试验模态分析技术也从最开始的单输入单输出(SISO)发展到了单输入多输出(SIMO)甚至是多输入多输出(MIMO)[9-11]。
目前变速器动态特性分析的研究多集中在轻型变速器[12-13],对于复杂的重型变速器研究相对较少。本文采用优于锤击法的激振器法(SIMO)对壳体进行自由模态测试[14]。本文分析了主副箱箱体间连接属性及有限元网格阶次对计算模态结果的影响,对比試验模态和计算模态提取了壳体非零前六阶模态的固有频率和振型。
1 壳体试验模态分析
1.1 试验模态参数识别理论
试验模态参数识别分为单自由度法、多自由度时域法和多自由度频域法。采用多自由度频域法下的最小二乘复频域法(LSCF)对模态参数进行识别。系统的输出和输入(频率响应函数)的关系为其中,[U(jw)]和[D(jw)]可以表示成如下形式:式中:m——输入通道数;
l——输出通道数;
[Ar]——分母矩阵多项式系数;
[Br]——分子矩阵多项式系数;
△t——时域数据采样间隔;
N——该数学模型的阶次。
LSCF求解可分为3步:1)求分母和分子矩阵多项式系数[Ar][Br];对实测的频响函数[H(jw)](取不同的频率w,组成维数足够多的方程组)利用最小二乘估计原理求出待定的分母和分子矩阵多项式系数;2)求模态参与因子和极点,将[Ar]构造成一个经过扩展的友矩阵,对其进行特征值分解,求得模态参与因子矩阵[L]m×m和极点si,[L]m×m的每一列向量{l}i代表激励对响应模态的比例贡献;3)求解模态振型,由实测的频率响应函数[H(jw)]、模态参与因子行向量{l}i和系统极点s,拟合函数方程,求解出第i阶模态振型{φ}i式中:[LR]——下残余项;
[UR]——上残余项。
1.2 试验条件
试验对象为某14档重型商用车变速器壳体。该变速器由前置副箱、主箱和后置副箱3个部分组合而成,箱体间采用螺栓连接。
主要试验设备:LMS.SCADAS数据采集前端,MB.Dynamics110型电磁激振器,MB.500Ⅵ型电荷放大器,PCB公司的三向ICP型加速度传感器,配备Test.Lab.14A的高性能计算机等。
1.3 试验参数设置
试验目的为测得变速器壳体在自由一自由边界条件下固有频率与振型。由于重型变速器壳体质量较大,不便于悬挂,因此将试件放在弹性轮胎上来进行自由边界条件的模拟。边界条件的选取对测试结果有很大影响,一般对于自由边界条件的模态分析,测试结果中得到支撑刚体固有频率要小于第一阶弹性体模态固有频率的10%[15]。
使用LMS.Testlab软件中MIMO FRF Testing模块进行数据的采集与分析。考虑尽量避开节点原则、充分反映壳体整体结构振动特性的原则、结合实际测试时的测试环境,壳体被离散成171个测点。离散的壳体测试模型如图1所示。
激励信号一般采用猝发随机,猝发随机信号可以最大限度减小泄露误差,适合平均掉结构可能存在的任何轻微非线性且共振峰处的相干性较好。激励点的初步选择根据计算模态的振型来确定,一般选择振型较大部位处的测点,避开模态节点位置;同时激励点选在能够使能量传到车身各个位置的刚度较大处。激励点的最终确定需要进行驱动点测试,找出能获得最多阶模态的测点。基于此,选择82号测点为激励点。
测试带宽选定为2048Hz,频率分辨率为IHz,5个测点采集一组数据,同步采集测点3个方向的振动响应,平均30次采样数据得到各测点频率响应数据。更换测点后需同步改变测点响应方向。
测试时,通道超过量程范围需舍弃该组数据,重新测定通道量程后再进行测试。每组数据采集时,相干函数基本在80%以上的信号为有效。变速器壳体正面测点测试完成时,基本不改壳体放置位置,保持同一激励点,调转壳体完成反面测点的测试。壳体测试部分布置如图2所示。
1.4 模态参数识别
采集完全部测点的频率响应数据后,基于“最小二乘复频域法(LSCF)"对该壳体的模态参数如固有频率及振型进行识别。采用LSCF法对测试数据进行分析得到表征壳体模态参数的稳态图。稳态图中物理极点的选择可确定壳体的固有频率和阻尼比,进一步计算得到对应振型。选择极点时,应选择波峰处且S点(极点的频率稳定、阻尼稳定、极点向量稳定)较多的极点,此外,可使用SUM函数(总的频率响应函数)和MIF函数(模态指示函数,在结构固有频率处显示极小值)来辅助极点选择。本次测试稳态图如图3所示。
如图所示,可看到该稳态图中总日U了频响函数曲线的第一个波峰(幅值很小),峰值处的横坐标即为支撑刚体固有频率。刚体固有频率为5.23Hz,远小于壳体第一阶固有频率370.85Hz,验证了该橡胶轮胎可以模拟自由模态测试中自由-自由边界条件。
1.5 模态验证
模态判断准则(MAC)可以当做一个工具来比较不同组的估计振型,或用以研究同一组中各估计模态的准确性。MAC矩阵计算如式(4)所示,对于同一个物理振型的估计{Ψ}和{Ψ}s,MAC值应当接近于1。而对于不同物理振型的估计,MAC值应该很低(振型正交性条件)。本次测试,不同阶次的模态振型MAC矩阵柱状图如图4所示,由图可知,本次试验提取的六阶模态为有效模态,非虚假模态,模态测试数据有效。
1.6 模态振型
试验自由模态非零前六阶振型如图5所示。
2 壳体计算模态分析
基于Hypermesh有限元分析软件,使用BlockLanczos法提取变速器壳体自由模态的模态参数。变速箱壳体材料为HT250,弹性模量为130GPa,泊松比为0.25,密度为7350kg/m3。为了获取更准确的计算模态参数,分别采用一阶和二阶四面体单元,对变速器壳体模型进行网格划分;主副箱箱体间的连接属性分别采用为Rbe2单元连接和面面接触(contact),以此来模拟实际的螺栓连接形式。根据网格参数属性的不同及主副箱体的连接形式不同,列出表1所示的4种模态计算方案。
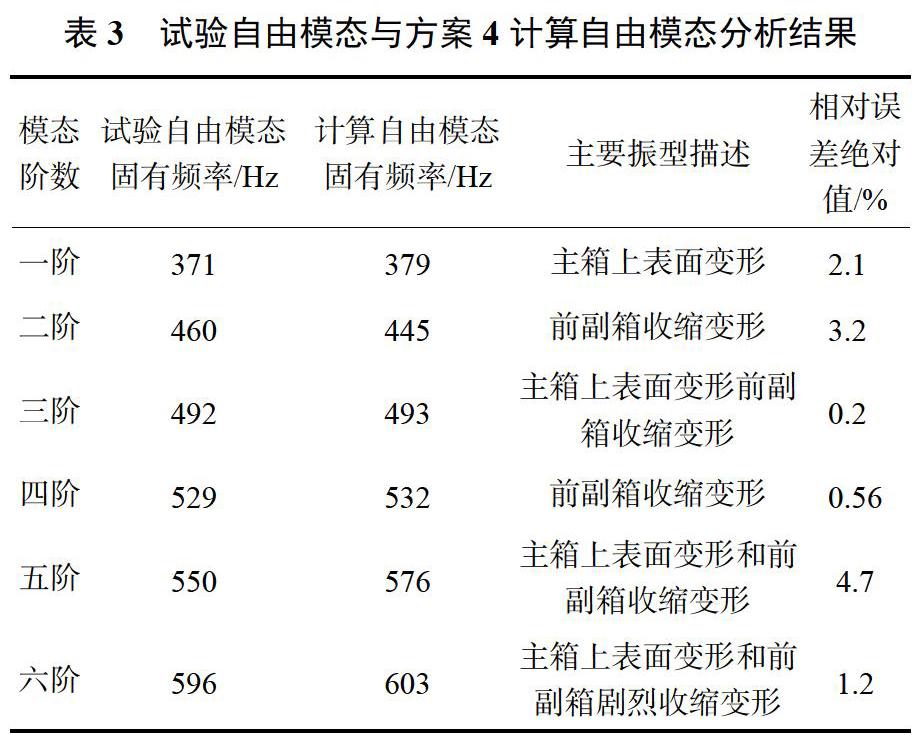
变速箱壳体在自由边界条件下的模态分析求解结果中,前6六阶为刚体模态,其固有频率基本接近于0,本文从第七阶开始,提取非零前六阶模态。为了便于与试验结果进行对比,称计算的第七阶模态为第一阶,第八阶为第二阶,以此类推。4种模态计算方案及试验模态所获取的六阶模态频率如表2所示。方案4振型如图6所示,振型描述如表3所示。
3 壳体试验和计算模态结果分析
分析表2数据可知方案4的计算自由模态固有频率更接近实际的试验自由模态固有频率,即对于该重型变速器的计算模态分析,面面接触更能模拟实际的主副箱体之间的螺栓连接,采用高阶单元能够获取更加准确的模态参数。
试验自由模态与方案4计算自由模态固有频率对比见表3。分析表3数据,两种方法获取的固有频率相对误差最大值为4.7%,小于5%;结合图5和图6及表3可知,各阶模态振型较为相似,因此可以得出以下结论:1)计算自由模态分析和试验自由模态分析皆可以有效地反映变速箱壳体的动态特性,表明了结构模态分析技术对结构动态特性分析的有效性;2)方案4计算自由模态分析的有限元模型精度较高,可以用于后续相应的有限元分析。
4 结束语
通过基于LMS.Test.Lab的试验自由模态和基于Hypermesh的计算自由模态对比分析,可得到如下结论:
1)试验自由模态分析时,边界条件极为重要,本文采用橡胶轮胎来模拟自由一自由边界条件达到了较好的测试结果,对于类似于该结构的被测对象(质量较大且不便于悬挂)在进行自由模测试时,可采用此种方法来进行自由边界条件的模拟;
2)计算自由模态分析的边界条件和单元阶次的选择极大地影响了最终结果,因此在进行计算模态分析时应全面考虑上述因素。对于该壳体的计算模态,主副箱体间的面面接触优于Rbe2刚性单元;对于计算模态分析而言高阶单元可以获取更加准确的模态参数;
3)通过试验自由模态和计算自由模态对比分析可知,两种方法所得到模态振型基本吻合,固有頻率误差较小,皆低于5%,说明所建立的有限元模型正确,且具有较高的精度。
参考文献
[1]施建光.三主轴立式加工中心整机动态性能分析与优化[D].合肥:合肥工业大学,2014.
[2]宫文峰,黄美发.倒装键合机支撑板模态参数提取与实验验证[J].中国测试,2014,40(5):145-148.
[3]李伟,许金凯,张向辉,等.五轴联动精密微铣削机床试验模态分析[J].中国测试,2016,42(7):123-126.
[4]韦海,邓良智,黄林凯.装载机变速箱壳体模态分析与测试[J].装备制造技术,2015(5):90-91.
[5]邓庆斌,王晓娟,王丽萍.电动汽车用变速器壳体的模态研究[J].汽车技术,2014(4):25-27.
[6]NAHVI H,JABBARI M C.Detection in beams usingexperimental modal data and finite element mode[J].International Journal of Mechanical Sciences,2005,47(10):1477-1497.
[7]向玲,鄢小安,陈涛.基于PolyMAX方法的悬臂梁振动模态分析[J].中国测试,2016,42(4):132-135.
[8]吕孟理,卢剑伟,季明微,等.某变速器壳体模态与异常振动分析[J].汽车实用技术,2017(17):120-121.
[9]BRECHER C,BAUMLER S,GURALLNIK A.Experimentalmodal analysis using a tracking interferometer[J].Manfacturing Technology,2014,63(1):345-348.
[10]AENLLE M L,BRINCKER R.Modal scaling in operationalmodal analysis using a finite element model[J].Intema tionalJournal of Mechanical Sciences,2013,76(6):86-101.
[11]NANGOLO N F,SOUKI月,J,RYCHLIKOVA L,et al.Acombined nunerical and modal analysis on vertical virbrationresponse of railway vehicle[J].Procedia Engineering,2014(96):310-319.
[12]孟凡龙,马维金,张纪平,等.汽车变速器壳体动态特性分析研究[J].机械传动,2016,40(3):98-101.
[13]蔡辉,翁建生,江星星.部分变速器壳体模态试验分析与验证团.轻型汽车技术,2015(3):43-47.
[14]龚亚器,杨啟梁,胡溧.汽车散热器散热管漏水故障分析[J].现代制造工程,2017(1):141-144.
[15]沃德·海伦,斯蒂芬·拉门兹,波尔·萨斯.模态分析理论与试验[M].白化同,郭继忠译.北京:北京理工大学出版社,2001:64.
(编辑:刘杨)
