情景分析与公司估值：模型选择、情景构建和概率测算

陈 蕾（博士生导师），张静文，莫荣团

一、引言

情景分析法作为一种预测事物未来发展态势的方法，最早于20 世纪70 年代被正式提出，并逐渐受到全球各大商业机构和政府机构的欢迎而被广泛使用。西方学术界在投资、军事、政治、图书情报、企业管理等多个领域对情景分析法的应用进行了研究。我国学术界于20世纪90年代逐渐引入情景分析法，涉及投资、交通规划、情报、能源、环境、物流等各大领域的应用研究。其中，在公司估值领域，一些学者建议，当未来不确定性显著增加时，可以尝试引入情景分析法，以使估值结果更加客观、合理[1]。

国外学者对情景分析法在公司估值中的应用开展了相对深入的探讨。Koller 等[2]提出，可以将情景分析法应用于新兴市场、高成长性公司以及周期性公司估值，并以双情景为例，根据评估对象的历史信息及近期经营状况和行业新形势，分析两种情景内容并确定相应概率，最后加权计算出不同情景下的公司价值。Damodaran[3]亦提出采用情景分析法对周期性公司进行估值，即评估各种情景下的预期现金流和公司价值，计算不同概率下的加权平均数，并强调要注意所有可能存在的情景不现实、不能覆盖所有可能风险以及双倍计入风险等问题。Massari、Gianfrate 和Zanetti[4]研究认为，情景分析法能帮助分析师和公司经理更好地理解和确定公司估值的相关风险，并总结了该方法的优缺点。

国内学者则多从某一类公司估值的创新思路或辅助工具入手，并对情景分析法加以考虑。例如，吴月琴、冯耕中[5]运用现金流量贴现法，辅以行业分析、微观经济分析和概率加权的情景分析，对网络企业进行估值，并建议将其推广应用到存在高度不确定性的其他新兴行业。郜志宇[6]在对矿业企业价值评估收益法的创新思路中提及情景分析法，并对其大致思路和应用步骤进行了简要描述。但是，已有研究在对不同情景进行加权平均的计算思路上存在一定分歧。一种观点认为，要分别预测未来不同情景下的公司价值并赋予不同的权重，最后计算公司的加权平均价值。例如，郜志宇[6]将情景分析法引入矿业企业的传统收益法估值过程，通过预测样本公司在不同情景下的净现金流、折现率和公司价值，计算其加权平均价值。另一种观点认为，要分别预测未来不同情景下的预期现金流并赋予不同的权重，在计算得到加权平均预期现金流后，再将其折现从而得到公司价值。例如，陈小伟[7]将情景分析法引入航运企业的传统收益法估值过程，通过对两阶段FCFF 模型中不同情景下的预期现金流分别进行加权平均后，再将其折现从而求得样本公司价值。

综上，国内外学者已围绕情景分析法在公司估值特别是收益法估值中的应用展开了研究，但涉及具体模型、应用难点和解决路径等方面的系统性研究不够丰富。这无疑不利于情景分析法在公司估值中的规范实践和有效应用。鉴于此，本文拟在已有研究的基础上，系统剖析情景分析法在公司估值中的应用思路、模型选择、情景构建和概率测算等关键问题，并结合案例对关键环节进行模拟演示，希冀为公司估值的方法选择和实务操作提供参考。

二、情景分析法在公司估值中的应用思路与模型选择

（一）情景分析法应用于公司估值的具体思路

参照已有研究，结合情景分析法的一般操作步骤，其应用于公司估值的具体思路如下：

1.明确估值对象及相关背景。明确要进行情景分析的标的公司，确定综合应用收益法和情景分析法来进行公司估值，具体通过分析公司背景与自身特征、明确评估基本事项、搜集重要内外部信息数据等，为后续分析提供依据。

2.识别影响估值的内部重要参数。影响估值的内部重要参数，主要是可能导致公司估值结果发生重大变化的内部影响因素，多体现为营业收入、营业成本、利润率、稳定增长率、资本性支出等不确定性较强的收益指标。要利用情景分析法对公司未来发展的不同可能情景进行预测和描述，必须先识别这些重要参数。

3.确定影响估值的关键外在驱动因素。影响公司估值的关键外在驱动因素通常包含宏观经济、政策法规、技术进步等，这些因素能够引起内部重要参数的波动，进而使公司估值结果发生重大变化。获得驱动因素相关信息的手段通常包括查阅电子或者纸质资料、访谈相关主体、询问权威专家等方式。

4.构建公司估值的未来情景框架并形成不同具体情景。将影响公司估值的关键外在驱动因素按照重要性和不确定性排序，总结形成未来情景框架，并依此形成不同具体情景。

5.测算每种未来情景对应的概率。描述各种具体情景，结合历史信息与当前时点的因素特征、先兆事件，采用适当的定性或定量分析方法，综合测算每种情景可能发生的概率。

6.分析标的公司在每种情景下的具体估值参数。针对不同具体情景，逐项分析公司估值的各项重要参数特征，此时需要考虑到各参数之间的联动关系，体现情景设定和参数组合的现实性和可行性，进而计算标的公司在每种情景下的收益额具体数值。例如，最佳情景并不意味着公司各项收益指标均为最佳，否则这种情景将不具有现实性。

7.通过加权平均计算得到公司估值结果。将情景分析思路与收益法估值思路相结合，选择和构建合适的公司估值计算模型，再将不同情景的发生概率、收益额等数据代入模型，进而加权计算得到估值结果。

（二）情景分析法应用于公司估值的模型构建与选择

1.情景分析法应用于公司估值的模型构建。为构建将情景分析思路与收益法估值思路相结合的公司估值具体模型，这里以FCFF两阶段模型为例，将其作为基本模型并引入情景分析过程中涉及的情景概率等相关参数。

首先，假设公司收益期为永续期，FCFF 在第n年（含第n年）以前有变化，在第n年（不含第n年）以后达到稳定状态并保持不变。则基本模型可以用公式表示为：

其中：P表示公司整体价值；FCFFt表示第t年的现金流；r表示折现率，具体采用加权平均测算得到；A表示公司收益达到稳定状态以后的年金；n表示公司收益达到稳定状态的时间（年）。

其次，根据已有文献提出的两种加权平均计算思路，即直接对不同情景下的公司价值进行加权平均的第一种思路，以及先对不同情景下的现金流进行加权平均再进行折现的第二种思路，分别构建将情景分析法应用于公司估值的具体模型。

这里暂假设不同情景下的公司收益额测算结果（FCFFt）存在显著差异，但折现率（r）以及达到收益稳定状态的时间（n）在不同情景下均保持一致。并且，无论采用哪种计算思路，同一公司的稳定收益（A）理论上应当相同。如果公司估值的未来情景被设定为m（m≥2且为整数）种不同具体情景，在经过未来情景构建、情景概率测算、情景内容分析、收益额测算等步骤以后，式（1）中的FCFFt、A、r、t等变量均为已知数，那么，按照第一种计算思路，引入情景概率（W）变量，直接对不同情景下的公司价值进行加权平均，则式（1）可变为：

其中：P1，P2，…，Pm分别表示第1，2，…，m 种情景下的公司整体价值；FCFFt1，FCFFt2，…，FCFFtm分别表示第 1，2，…，m 种情景下的 FCFFt；W1，W2，…，Wm分别表示第1，2，…，m种情景的发生概率，即权重。

而在同样的假设下，按照第二种计算思路，先对不同情景下的现金流进行加权平均再进行折现，则式（1）可变为：

2.情景分析法应用于公司估值的模型选择。通过比较上述模型推导过程不难看出，只要r和n在不同情景下均保持一致，通过式（2）和式（3）得到的估值结果就会完全一样，即两种加权平均计算思路并无本质差异，只是在操作步骤上存在计算顺序的不同。此时，并不存在具体模型的选择问题。

但是，这并不代表基于两种加权平均计算思路构建的估值模型就是彼此相同。其关键在于r和n在不同情景下是否会存在不同取值。事实上，在构建未来不同具体情景时，公司收益额从评估时点发展至内在稳定状态，可能需要经历不同的时间长度，即公司在不同情景下的n可能并不相同。同理，公司在不同情景下所面临的风险也往往不同，即不同情景下的r亦可能存在差异。

对此，若假设r 和n 在不同情景下均不相同，那么，通过式（2）和式（3）得到的估值结果势必彼此不同，由式（3）得到的加权平均现金流甚至已不再适合采用不同的折现率和收益期进行折现。于是，基于第一种加权平均计算思路的估值模型［式（2）］成为优先选择的模型，式（2）相应变为：

其中：n1，n2，…，nm分别表示第1，2，…，m种情景下公司收益达到稳定状态的时间；r1，r2，…，rm分别表示第1，2，…，m种情景下在第一阶段适用的折现率；r表示公司收益达到稳定状态后的折现率。

需要强调的是，参考Damodaran[3]的研究，将情景分析法应用于公司估值时，须注意双倍计入风险等问题。“双倍计入风险”意味着预期价值已经被调整过风险，所以，潜在的相同风险可能被双倍计入，或双倍计入了与决策不相关的风险。应该看到，本文已经通过不同情景下的收益额预测将公司可能面临的不确定性风险考虑在内，如果再对折现率进行相应的情景分析并赋予不同权重，则可能存在重复性操作、双倍计入风险的问题。因此，本文认为，在选择情景分析法进行公司估值时，应考虑选用正常化的折现率[8]即公司收益达到稳定状态以后的折现率，作为不同情景下的折现率取值依据，即r1=r2=…=rm=r。故式（4）可进一步变为：

其中：P1，P2，…，Pm分别表示第1，2，…，m种情景下的公司整体价值；n1，n2，…，nm分别表示第1，2，…，m 种情景下公司达到收益稳定状态的时间；FCFFt1，FCFFt2，…，FCFFtm分别表示第 1，2，…，m种情景下的FCFFt；W1，W2，…，Wm分别表示第1，2，…，m种情景的发生概率，即权重；r表示公司收益达到稳定状态后的折现率，具体采用加权平均测算得到；A表示公司收益达到稳定状态后的年金。

综上所述，论及情景分析法在公司估值中的模型构建及其选择问题，直接对不同情景下公司价值进行加权平均的估值模型［式（5）］具有最广泛的适用性，成为可供选择采用的最佳模型。虽然本文只是以FCFF 两阶段模型为例，探索情景分析法在公司估值中的具体模型及选择问题，但如果继续以收益法的其他模型进行分析，亦可形成类似结论。

（三）情景分析法应用于公司估值的难点分析

1.未来情景构建。构建公司估值的未来情景框架并形成不同具体情景，需要分别明确未来可能情景的数量及各自特征。此时，需要将宏观经济、政策法规、技术进步等影响公司估值的关键外在驱动因素按照重要性和不确定性排序，总结形成未来情景框架，并依此形成不同的具体情景。这一环节对于公司估值的整体过程而言至关重要，涉及整个分析框架的合理性，并为后续的重要参数估计奠定基础，将直接决定情景分析法的应用效果。因为情景分析法的评价标准主要就在于情景之间的连贯性、情景综合性、不同情景的内部相同性、情景新颖性、情景结构分析和逻辑基础的严谨性。如果要满足以上各项评价标准，难度很大。

2.情景概率测算。测算每种未来情景对应的概率，即分别度量式（5）中的“W1，W2，…，Wm”，需要通过描述各种具体情景，结合历史信息与当前时点的因素特征、先兆事件，采用适当的定性或定量分析方法，综合测算每种情景可能发生的概率。这一环节同样是公司估值整体过程中的关键环节，在很大程度上决定着整个分析框架及情景分析法估值结果的可靠度。对于这一问题，已有研究多是对各种未来情景的宏观经济走势、公司所属行业发展趋势等进行定性分析，继而直接推测每种情景的发生概率。而如何综合采用定性与定量分析估算每种情景发生的概率，并提高参数预测的合理性和可靠性，成为情景分析法的另一大难点环节。

三、情景分析法应用于公司估值的未来情景构建

在明确估值对象及相关背景、识别影响估值的内部重要参数、确定影响估值的关键外在驱动因素以后，对于未来情景构建这一难点，本文拟从识别关键外在驱动因素、关键外在驱动因素排序、设置未来情景的数量、划分不同情景的内容、构建情景轴等方面探索解决路径。

（一）关键外在驱动因素的识别

在识别外在驱动因素时，应尽可能全面地列出影响公司估值的关键外在驱动因素。前已述及，宏观经济、政策法规、技术进步等是影响公司估值的常见外在驱动因素。以某能源公司为例，对其关键外在驱动因素的识别详见表1。

表1 关键外在驱动因素及其评价指标

通常情况下，关键外在驱动因素的识别和确定由专家讨论分析确定，除此之外，也可以采用PEST分析、STEEP 分析、PESTLE 分析、波特五力分析等方法。以PESTLE分析为例，可以分别从政治、经济、社会、资源、环境、技术等方面进一步细化外在驱动因素。常见的外在驱动因素分类见表2。

表2 常见的外在驱动因素分类

（二）关键外在驱动因素排序

对于前期形成的外在驱动因素列表，按照重要性和不确定性排序，一般将关键外在驱动因素控制在五个以内，最重要、不确定性最强的因素成为首选因素。此排序环节可以借助平面直角坐标系进行，如图1所示。

图1 未来情景构建中的关键外在驱动因素排序

图1 中，落入第Ⅱ象限的因素是情景框架构建中最为关键的因素，其次是落入第Ⅱ象限和第Ⅲ象限的因素，最后是落入第Ⅳ象限的因素。当然，不同行业样本公司的关键外在驱动因素可能相同，亦可能不同，需要针对具体公司进行具体分析。

此外，当驱动因素较多时，还可以采用重要性与不确定性矩阵对驱动因素进行排序。

（三）设置未来情景的数量

根据排序选择的关键外在驱动因素构建情景时，一般需要筛选并设置2个（含）以上未来情景，例如双情景、三情景、四情景、五情景等多种形式。在多数情况下，应用情景分析法所构建的项目未来情景的总数不超过5个，但在个别情况下，也不排除会根据具体需要而设计5 个以上未来情景的可能。未来情景设置数量的多少，一般取决于经排序选择的关键外在驱动因素的数量。对于公司估值，这些情景应尽可能涵盖目标公司估值涉及的各项关键估值参数与外在驱动因素。表3 较为直观地列示了常见的情景框架设计方案。

（四）划分不同情景的内容

与设置未来情景的数量紧密相关的是，根据不同情景的各自特征，对其进行内容划分。这里以双情景和三情景为例，进一步列举常见的情景内容划分方案，详见表4和表5。

根据表4，双情景通常被划分为情景1和情景2、积极情景和消极情景、乐观情景和悲观情景、事件发生情景和事件不发生情景等不同内容。除了第一种划分方法未体现具体情景特征，其他划分方法中的两种情景均是属性分明、对立性较强。所以，双情景分析更适用于关键外在驱动因素非常少的情形；并且在多数情况下，其中只有一个驱动因素是不确定性最强又最重要的。

表5 常见的三情景内容划分方案

根据表5，三情景通常被划分为情景1、情景2和情景3，分别包括高情景、中情景、低情景，乐观情景、中性情景、悲观情景，繁荣情景、正常情景、衰退情景，协调发展情景、基准增长情景、风险情景等不同内容。显然，相较于双情景，三情景增加了一种处于中间地带的情景，使三种情景之间的对立性有所减弱。这是因为涉及的关键外在驱动因素数量有所增加，或者不确定性最强又最重要的驱动因素并非是只有一个，从而降低了单一因素的重要性或不确定性。

可见，关键外在驱动因素的数量越少且其重要性和不确定性比重越大，需要设置的未来情景数量就越少，不同情景之间的对立性也就越强；反之，需要设置的未来情景数量越多，不同情景之间的对立性也越弱。

（五）构建情景轴

此处提出的“构建情景轴”，实际上是“设置未来情景的数量”和“划分不同情景的内容”的补充手段。因为公司未来情景的发展，主要取决于高重要性、高不确定性驱动因素之间的相互联系，而通过情景轴可以将各种驱动因素联动并构建公司的逻辑分析框架，有利于明确未来情景的数量和内容。例如，假设借助平面直角坐标系，已经从高重要性、高不确定性的驱动因素中选取宏观经济、产业政策、技术进步这3种关键因素，那么在制定情景框架设计方案时，可以先对其构建不确定轴面。详见图2。

图2 构建情景轴示例

图2 中，轴面圆圈内区域分别代表宏观经济不景气、产业政策中性、技术进步慢；靠近坐标轴指向的一端分别代表宏观经济景气、产业政策利好、技术进步快。据此根据三项驱动因素的特征设计情景框架，进而划分好情景并描述其内容。情景框架设计见表6。

表6 未来情景框架设计示例

四、情景分析法应用于公司估值的情景概率测算

对于情景概率测算这一难点，本文尝试采用历史财务信息分析法、概率树分析法、交叉影响分析法等三种估算方法探索解决路径。

（一）基于历史财务信息测算未来情景的概率

历史财务信息分析法，就是通过分析公司历史年度财务信息，研究各年度收益增长率和测算其分布特征，并结合公司当前在整个经济周期中位于波峰、中段或波谷的阶段分析，判断未来走势的概率分布。在测算各年度收益增长率的分布特征环节、评估人员选取以评估基准日为倒推起点的研究时段时，应尽可能涵盖若干个完整的经济周期。不过，这种估算思路特别适用于周期性公司估值的情景概率测算，以及关键外在驱动因素非常少的情形，尤其是双情景情形。

下文将结合一个公司估值案例对历史财务信息分析法进行说明。X公司成立于1997年1月，是主营钢铁及炉料销售的上市公司，评估基准日为2018年12 月31 日。经预测，对X 公司的未来发展趋势适合采用双情景进行分析，具体可划分为乐观情景和悲观情景。如果X公司未来的平均净利润增长率大于零，则为乐观情景；如果X公司未来的平均净利润增长率小于零，则为悲观情景。参照刘树成[9]的研究，从整体来看，我国经济平均以9年左右为一个周期。据此，假设2000 ～2017 年我国恰好经过两个完整的经济周期。通过对X公司2000 ～2017年17个净利润增长率的可观测值进行分析，发现其中53%为正值，47%为负值，详见表7。

表7 2000～2017年X公司净利润增长率分析

根据表7，可以判断X 公司未来发展处于乐观情景的概率大致为53%，面临悲观情景的概率大致为47%。

（二）采用概率树分析法测算未来情景概率

基于历史财务信息测算未来情景的概率，多适用于关键外在驱动因素非常少的情形。当关键外在驱动因素较多时，可以采用概率树分析法测算未来情景概率。概率分析，又称风险分析，是通过研究各种不确定性因素发生不同变动幅度的概率分布及其对项目经济效益指标的影响，对项目可行性和风险性以及方案优劣作出判断的一种不确定性分析法。概率树分析法则具体将各种不确定性因素之间的逻辑关系用一种称为概率树的树形图表示。

下文结合一个公司估值案例对概率树分析法进行说明。

Y 公司是以加工、销售有色金属为主业的上市公司。经预测，影响Y公司估值的最关键外在驱动因素有两个：宏观经济发展水平和产业政策支持力度，假设两个关键驱动因素之间相互独立。通过进一步聘请专家对这两项关键外在驱动因素的可能性做出合理假设判断，并对每一种可能性进行赋值，宏观经济未来可能呈现良好发展（中高速发展）和低速发展两种情形，发生概率分别为60%和40%；产业政策未来可能呈现支持政策和中性政策两种方向，发生概率分别为60%和40%。可见，Y 公司适合采用四情景进行分析，具体可划分为情景1、情景2、情景3 和情景4。据此，绘制Y 公司未来情景的概率树分析图，详见图3。

图3 Y公司未来情景的概率树分析图

根据图3，如果各关键驱动因素之间相互独立，则可以将每个关键驱动因素的各种可能性概率与其他关键驱动因素的各种可能的概率分别相乘，进而组合计算得到未来各种情景的发生概率。测算结果如下：

1.情景1。宏观经济以良好水平发展，并且有色金属行业得到政府政策的支持，这是乐观情景。将良好发展的宏观经济和支持性产业政策的发生概率相乘，即60%×60%=36%。36%就是情景1发生的概率。

2.情景2。宏观经济以良好水平发展，并且有色金属产业政策保持中性，任其自然发展，这是次优情景。将良好发展的宏观经济和中性产业政策的发生概率相乘，即60%×40%=24%。24%就是情景2发生的概率。

3.情景3。宏观经济以低速水平发展，并且有色金属行业得到政府政策的支持，这是一般情景。将低速发展的宏观经济和支持性产业政策的发生概率相乘，即40%×60%=24%。24%就是情景3 发生的概率。

4.情景4。宏观经济以低速水平发展，并且有色金属产业政策保持中性，任其自然发展，这是悲观情景。将低速发展的宏观经济和中性产业政策的发生概率相乘，即40%×40%=16%。16%就是情景4发生的概率。

因此，Y公司未来情景1、情景2、情景3 和情景4 的发生概率分别为36%、24%、24%和16%。以上是关键外在驱动因素为2 个的四情景情形下的公司估值案例分析，概率树分析法亦可被用于情景设置更为复杂、关键外在驱动因素更多的公司估值与决策。

（三）采用交叉影响分析法测算未来情景概率

概率树分析法是假设各外在驱动因素之间相互独立的一种理想化的概率测算方法。事实上，许多外在驱动因素的变动具有关联性，某一驱动因素的变动可能导致其他驱动因素发生变动。当外在驱动因素之间存在关联关系时，可以尝试进一步引入交叉影响分析法。交叉影响分析法作为一种系统预测技术，于1968 年由海沃德（Hayward）和戈登（Gordon）首先提出。该方法综合了专家调查法、主观概率法、因果分析、蒙特卡罗模拟等一系列预测技术，以确定一组目标的相互影响程度及未来发生的概率。因此，本文可以利用交叉影响分析法对公司估值的关键外在驱动因素之间的关联关系进行分析，并对关键外在驱动因素的初始概率进行修正，再通过概率树分析法计算未来情景的概率。下面分别对基于蒙特卡罗模拟的交叉影响分析、基于马尔科夫链的交叉影响分析、基于贝叶斯规则的交叉影响分析进行应用模拟。

1.基于蒙特卡罗模拟的交叉影响分析。根据交叉影响分析法的思路，当一种驱动因素事件发生时，在一定程度上会影响到其他驱动因素事件发生的概率，此时可以根据式（6）对各因素交叉影响下的事件发生概率进行修正。但由于一次性修正后的概率准确度仍然有限，所以可以继续使用蒙特卡罗模拟技术对其进行调整。

其中：Pn表示某驱动因素事件发生前，第n个驱动因素事件发生的初始概率值；KSn表示第n个驱动因素事件受该驱动因素事件的影响方向和程度；P'n则为该驱动因素事件发生后第n个驱动因素事件发生的修正概率值。这里继续以Y 公司估值为例对基于蒙特卡罗模拟的交叉影响分析进行说明。

（1）假设宏观经济发展水平和产业政策支持力度这两个关键外在驱动因素之间具有关联性。除此之外，其他预测信息保持不变，即宏观经济良好发展（事件A1）的初始概率为60%，产业政策支持（事件A2）的初始概率为60%。

（2）专家根据因素交叉影响程度参照表（详见表8），对Y公司关键外在驱动因素事件的KS值进行评分，由此整理得到事件A1和事件A2之间的相互影响方向和程度，详见表9。

从表 9 可知，当事件 A1发生时，对事件 A2有50%的正向影响；当事件A2发生时，对事件A1也有20%的较弱的正向影响。

（3）参考任海英等[10]的研究，按照以下步骤，利用式（6）和蒙特卡罗模拟实验进一步计算事件A1和事件A2发生的修正概率。

表8 因素交叉影响程度参照表

表9 Y公司关键外在驱动因素事件发生的初始概率及相互影响的方向和程度

第一，从其他因素事件集合中随机选取某一事件，根据0 ～99随机数表，将随机数与因素事件发生的初始概率相比较。如果随机数小于或等于事件发生的概率，则假设该事件发生，需要对其他事件的发生概率进行修正；反之，则假设该事件不发生，并保持其他事件的发生概率不变。在本案例第一次模拟中，假设随机选取出事件A1，且随机数为49，位于0～60 区间内，则认定事件A1发生，并修正事件A2的发生概率P2，得到P'2=0.60+0.50×0.60×（1-0.60）=0.72。当然，如果随机数不在0 ～60区间内，则说明事件A1不发生，不需要对P2进行调整。

第二，再次从其他因素事件集合中随机选取某一事件，按照更新后事件发生的概率重复以上步骤。在本案例中，继续选择事件A2，假设随机数为53，位于0 ～72区间内，所以认定事件A2发生，同样的修正事件A1的发生概率P1，得到P'1=0.60+0.20×0.60×（1-0.60）=0.648。与上述分析相似，如果随机数不在0 ～72区间内，则说明事件A2未发生，不需要对P1进行调整。

第三，重复以上两个步骤，对因素事件集合中的所有事件都进行一次判断——发生或者不发生，至此，完成一次模特卡罗模拟实验。在本案例中，因为只有2个因素事件，所以已经完成一次模拟。

第四，重复以上三个步骤，进行x次蒙特卡罗模拟实验，并采用整个过程中各因素事件发生的频率作为事件发生的最终修正概率。即在x次实验中，如果某一因素事件发生的次数为m，则认为其发生的修正概率为：

一般来说，需要经过1000次以上的模拟实验才能形成精确度较高的结果，因此有必要借助计算机软件进行模拟操作。在本案例中，仅以100次模拟实验为例进行简要说明。例如，通过100次蒙特卡罗模拟，事件A1发生了61次，事件A2发生了63次。则P''1=0.61，P''2=0.63。即事件A1和事件A2发生的修正概率分别为61%和63%。

（4）将因素事件的修正概率值应用于前文介绍的概率树分析法，进而测算公司估值的未来情景概率。对于Y公司，在考虑到不同关键外在驱动因素间的关联性后，宏观经济未来可能呈现良好发展和低速发展的发生概率分别为61%和39%；产业政策未来可能呈现支持政策和中性政策两种方向的发生概率分别为63%和37%。由此，通过概率树分析法计算得到未来情景1、情景2、情景3和情景4的发生概率分别为38.43%、22.57%、24.57%和14.43%。需要说明的是，随着模拟试验次数的增加，这一估算结果还会有变动的空间。

2.基于马尔科夫链的交叉影响分析法。许多学者尝试对传统交叉影响分析法提出改进方案，以求简化复杂的计算过程。其中，将马尔科夫决策分析方法与交叉影响分析法相结合可视为一种相对有效的概率修正方法[11]。马尔科夫预测模型，是根据事件目前的状况预测未来各个时刻变动状况的一种方法，其原始模型是马尔科夫链。马尔科夫链的基本特征是在时间序列上具有无记忆性，即事物发展的当前状态仅与较前一个时间段所处的状态相关，而对更早的时间没有依赖性。基于马尔科夫链的交叉影响分析法的核心，则是将各情景下的初始概率和各情景之间的条件概率，转化为马尔科夫状态的初始概率和一步状态转移概率。

本文将需要预测的公司估值的所有外在驱动因素看作一个整体，将各个驱动因素事件的概率占全部驱动因素事件的概率之和的比重组成矩阵，用P表示；再将因素事件发生的初始概率转化为马尔科夫链下的初始概率p（0），P则作为马尔科夫链的一步转移概率矩阵；经预测分析，第n次实验后稳定状态的矩阵可以由式（8）得到，P（n）即为经过调整后的各驱动因素事件发生概率的占比；然后，将初始概率之和与稳定状态矩阵相乘，由式（9）便可以得到最终的修正概率。

（1）以Y公司估值为例，对基于马尔科夫链的交叉影响分析进行说明，相关预测信息、驱动因素事件的初始概率及相互影响情况与上例完全相同。首先，事件A1和事件A2的初始概率之和为∑Pn=1.2，以此构建马尔科夫链初始状态矩阵P（0）及转移矩阵，如下所示：

（2）进一步得到矩阵P1和最终的马尔科夫稳定状态矩阵p（n），如下所示：

（3）通过式（9），计算得到事件A1和事件A2的修正概率，分别为0.5852和0.6148，见下式和表10。

P=（0.6+0.6）×p（n）=（0.5852 0.6148）T

表10 Y公司关键外在驱动因素事件发生的初始概率及修正概率比较

（4）将此修正概率值同样应用于概率树分析法，计算得到Y公司估值的未来情景1、情景2、情景3和情景4 的发生概率，分别为35.98%、22.54%、25.50%和15.98%。

3.基于贝叶斯规则的交叉影响分析法。贝叶斯规则也提供了一种计算概率的方法，具体是先对未知参数的先验信息与样本信息进行综合，再根据贝叶斯公式计算得到后验信息，为情景概率测算提供了另一思路[12]。该思路需要基于先前财务数据或主观判断的起点概率（初始概率），结合新的信息（特征向量）不断调整（后验概率），其中的特征向量便是通过因素间的交叉影响强度矩阵分析得到。比较具有代表性的巴特尔研究所的BASIC 方法便基于此而产生，其可通过IFS软件实现计算。

下面将参考Y 公司估值案例信息，对基于贝叶斯规则的交叉影响分析进行说明。其中，公司预测信息和驱动因素事件的初始概率取值与上例相同，但为了更好地演示基于贝叶斯规则的交叉影响分析过程，此处各因素事件互相影响的情况具有不同假定条件，即其间存在正面（＋）、负面（-）和无影响（0）等三种情况，并以此构建交叉影响强度矩阵，如表11所示。

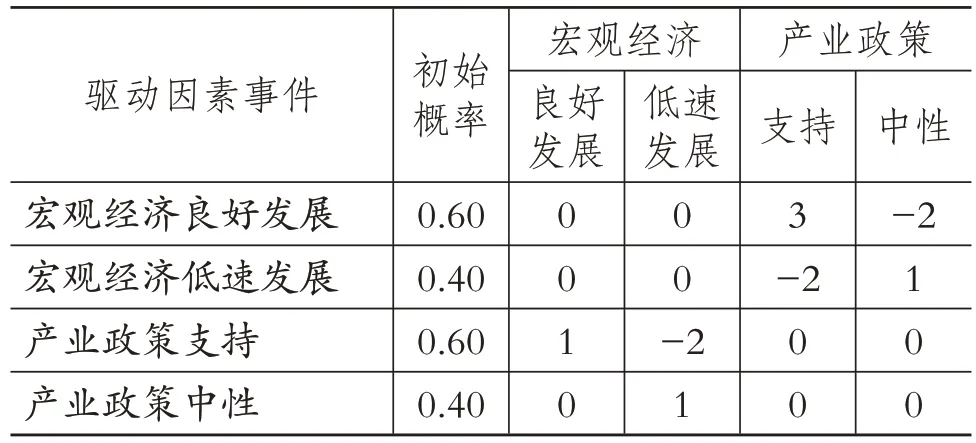
表11 Y公司关键外在驱动因素事件的交叉影响强度矩阵

（1）根据关键外在驱动因素事件的交叉影响强度矩阵计算交叉影响系数。其中，当交叉影响强度大于或等于零时，交叉影响系数取值为“交叉影响强度+1”；当交叉影响强度小于零时，交叉影响系数取值为“1/（1-交叉影响强度）”。据此，由表11 得到交叉影响系数矩阵B1：

（2）将判断矩阵的每一列元素作归一化处理得到矩阵B2：

利用和积法计算特征向量，得到特征向量WT=［0.28 0.24 0.22 0.26］T。

（3）利用“初始概率×特征向量”计算出后验概率，再通过计算同一驱动因素在不同事件内容下的后验概率占比求得相应的修正概率。计算结果如表12所示。

（4）将此修正概率值同样应用于概率树分析法，可以计算得到Y 公司估值的未来情景1、情景2、情景3 和情景4 的发生概率，分别为35.84%、28.16%、20.16%和15.84%。

表12 Y公司关键外在驱动因素事件的后验概率

五、结论

情景分析法为高度不确定性下的公司估值提供了新思路，其特别适用于增长性公司的估值和周期性公司的估值。本文系统地剖析了情景分析法在公司估值中的应用思路、模型选择、情景构建和概率测算等关键问题，并结合案例进行模拟演示，希冀为公司估值的方法选择和实务操作提供参考。研究结论如下：

情景分析法在公司估值中的应用思路可体现为七个步骤：①明确估值对象及相关背景；②识别影响估值的内部重要参数；③确定影响估值的关键外在驱动因素；④构建公司估值的未来情景框架并形成不同具体情景；⑤测算每种未来情景对应的概率；⑥分析标的公司在每种情景下的具体估值参数；⑦通过加权平均计算得到公司估值结果。

通过对情景分析法应用于公司估值的两种加权平均计算思路的比较，发现只要折现率和达到收益稳定状态的时间在不同情景下均保持一致，这两种计算思路并无本质差异，只是在操作步骤上存在计算顺序的不同。但是，直接对不同情景下公司价值进行加权平均所构建的估值模型具有更广泛的适用性，应被视为优先选择的模型。

未来情景构建和情景概率测算是情景分析法应用于公司估值的两大难点环节。对于第一个难点环节，建议从识别关键外在驱动因素、关键外在驱动因素排序、设置未来情景数量、划分不同情景内容、构建情景轴等方面构建未来情景；对于第二个难点环节，建议采用历史财务信息分析法、概率树分析法、交叉影响分析法等估算方法测算情景概率。其中，交叉影响分析法可进一步细分为基于蒙特卡罗模拟的交叉影响分析、基于马尔科夫链的交叉影响分析、基于贝叶斯规则的交叉影响分析等三种思路，这三种思路都在一定程度上有助于对公司估值的未来情景概率进行判断。