深度学习与人脸识别算法研究

张卓群 曹钟淼 王慧 刘洪普

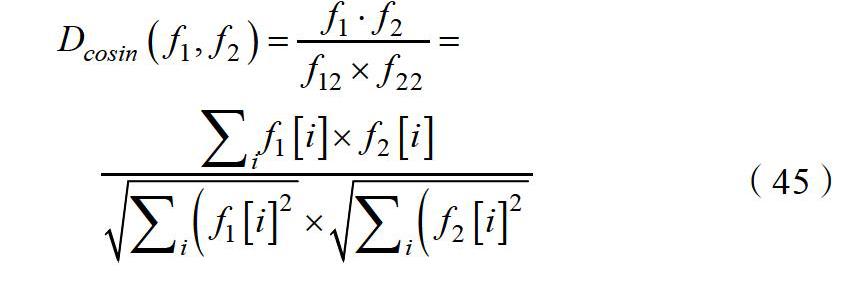
摘  要： 目前人脸识别技术已经得到了较多的应用，包括在安检工作、金融工作以及交通等领域中，其稳定性强、识别精度高，市场应用前景广阔，能够为用户信息的识别提供更便捷的服务。随着对人脸识别研究的深入，出现了更多的算法，最初大多都是提取浅层特征来进行分析，并采用特征融合的方式识别，在最后的识别过程中主要利用了联合贝叶斯分布等机器学习分类器进行处理。这种方法虽然能够达到一定的识别效果，但是精度不高，容易受到多种外部因素（光照、遮盖等）的影响，降低了识别结果的準确性。本文主要对人脸识别的框架进行了研究与分析，首先设计了人脸识别框架，然后对深度学习人脸识别算法的几个重要组成部分进行了分析与研究，主要包括人脸对齐模块、人脸特征提取、人脸识别验证模块等。

关键词： ：人脸识别;人脸对齐; 人脸特征提取;深度学习

中图分类号： TB302.6    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.09.046

本文著录格式：张卓群，曹钟淼，王慧，等. 深度学习与人脸识别算法研究[J]. 软件，2019，40（9）：199-204+208

Research on Deep Learning and Face Recognition Algorithms

ZHANG Zhuo-qun， CAO Zhong-miao， WANG Hui， LIU Hong-pu^*

（Hebei University of Technology， Tianjin 300000）

【Abstract】： At present， face recognition technology has been applied widely， including security， financial and transportation fields， which can provide convenient services for user information recognition for its strong stability， high recognition accuracy and broad market application prospects. With deepening research on face recognition， more and more algorithms have emerged. At first， most of them extract shallow features for analysis， and recognize based on feature fusion. During final recognition process， carry on process with machine learning classifiers such as Joint Bayesian Distribution. Although the method can achieve some certain recognition effect， it has less accuracy for being influenced by variety of external factors （illumination， occlusion， etc.）. The paper studies and analyzes framework of face recognition. Firstly， it designs framework of face recognition. Secondly， its analyzes and studies several important parts of deep learning face recognition algorithm， including face alignment module， face feature extraction， face recognition verification module and etc.

【Key words】： Face recognition; Face alignment; Face feature extraction; Deep learning

0  引言

目前人脸识别技术已经得到了较多的应用，包括在安检工作、金融工作以及交通等领域中，其稳定性强、识别精度高，市场应用前景广阔，能够为用户信息的识别提供更便捷的服务。

随着对人脸识别研究的深入，出现了更多的算法，最初大多都是提取浅层特征来进行分析，并采用特征融合的方式识别，在最后的识别过程中主要利用了联合贝叶斯分布等机器学习分类器进行处理。这种方法虽然能够达到一定的识别效果，但是精度不高，容易受到多种外部因素（光照、遮盖等）的影响，降低了识别结果的准确性。

深度學习（Deep Learning，DL）最早来源于神经网络的研究，但是目前仍没有形成明确的定义。深度学习可以建立与人脑相似的神经网络，便于按

照人脑的方式对不同类型的数据进行处理。深度学习采用简单的表达形式来描述复杂问题，使得复杂的问题简单化。随着学者在机器学习算法研究方面的投入，深度学习算法得到了较大的发展，基于人脑工作方式进行分析，能够实现对图像、文本等数据类型的处理。深度学习需要逐步使用模型输出逼近预期的结果。从这个角度来说可以对实际输出结果与预期目标结果的偏差进行分析，并将其应用到对权重矩阵的更新中。除了在数据处理方面的应用，深度学习算法还在生物学、地理学以及油气勘探等领域到获得了较多的应用。尤其是随着云计算技术以及深度学习理论的进一步发展，未来深度学习将会有更广阔的应用前景，能够为人们带来更多高质量的计算服务^[1]。深度学习算法逐步应用到了更多的领域中，特别是在图像处理以及人脸识别方面，很多研究人员设计了不同的人脸识别算法，并利用LFW等数据集验证了算法能够达到的效果。深度学习算法的优势在于能够提升人脸识别过程中的抗干扰能力，其主要是提取图像的高层次特征，从图像全局来获取最本质的特征信息，降低了人脸表情变化以及光线等因素的影响，提升了识别结果的准确性。从这个角度来说，人脸识别其实是一种特征提取问题，基于深度学习的人脸识别技术具有广阔的应用前景。

1  深度学习算法相关研究

1.1神经网络概述

神经元的具体结构即为图1中所示，其是神经网络内的最小单元，一个神经元内包括多个组成要素，例如有阈值、激活函数、权值以及输入输出等，利用突触连接权值可以对各个神经元之间的连接强度进行表示，其值有正有负，如果是正值^[2-5]，则说明神经元的状态是激活的，相反的说明神经元处于未激活状态。利用加法器可以对各个输入的总效果进行分析，由于不同的神经元在作用强度方面具有一定的差异性，可以将其对后一个神经元的总作用效果表示为神经元的线性加权之和。采用激活函数能够有效地对神经元的输出进行控制，使其保持在正常的范围内，这个范围一般是[-1，1]或者是[0，1]。具体结构如下。

图中表示神经元的输入，表示两个神经元的连接权值，，分别代表的是阈值与输出，代表激活函数。假定表示输入信号的加权之和，可以将神经元结构表示为如下：

（1）

（2）

代入之后可以得到

   （3）

假定，代入上述公式得到

（4）

将，代入可以得到公式

  （5）

所以有

  （6）

1.2  RBF神经网络

RBF代表的是径向基函数方法，这种方法最初主要用于对多变量的插值问题进行处理，即在输入变量与输出变量之间获取一个满足特定条件的非线性函数，输入变量与输出变量分别表示为 与，的形式如下所示：

  （7）

上述公式代表的是一个插值曲面，Lowe 等人利用径向基函数方法对神经网络进行了设计，并得到了RBF神经网络，输入与输出之间的映射关系即为公式（7）中所描述。

已知空间点集合，点数目为N，表示n维向量，对应的实数集可以表示为，二者的映射关系可以表示为如下公式：

，   （8）

在选取N个基函数之后，可以计算其线性加权之和，即得到

    （9）

公式中的代表基函数，即为基函数j的中心，表示X與之间的距离。公式代入之后可以得到如下方程组：

（10）

根据，可以将上述公式表示成

（11）

对上述矩阵进行简化之后得到

（12）

其中表示一个插值矩阵，其大小为，與分别表示权值矩阵与输出矩阵。如果是可逆的，可以得到

（13）

根据Micchelli定理可知，当完全不同时，满足可逆条件。

1.3 BP神经网络

反向传播的详细过程如下所示：第一步是对神经网络进行构建，并任意设置各个神经元的权重;接着需要对输入模式进行设置，并得到网络的输出值，然后将其与预期输出值进行对比，分析其差值是否达到了预期的标准。根据其差值对权重进行调节，直到二者的差值足够小，也就是实际输出接近于预期输出。按照这种方式开始从输出层向输入层逐层逆推，逆推到首个隐含层时结束。详细的计算过程如下所示^[6]。

首先设置输入样本数目为p，分别表示为，所有样本输入完成之后，可以得到输出，此时的样本误差可以表示为

（14）

其中代表的是期望输出。根据这种方式可以得到网络的全局误差，其公式如下所示

（15）

权值变化的计算公式如下所示

（16）

信号误差的计算公式如下所示

（17）

将公式14代入上述公式可以得到

 （18）

   （19）

在公式17中代入18，19可以得到如下

    （20）

   （21）

輸出层神经元的权值调整公式如下所示

  （22）

隐含层权值变化如下所示

   （23）

误差信号公式如下

    （24）

  （25）

其中

     （26）

第二项是

   （27）

因此可以得到

     （28）

  （29）

此时隐含层的权值调整公式如下

（30）

2  人脸识别算法框架设计

人脸识别算法框架主要用于对人脸特征的提取，人脸识别算法框架模块即为图2中所示，其中含有多个模块，例如有人脸对齐、特征提取以及特征运用等模块。按照各个模块的作用顺序，首先是人脸对齐模块，主要用于原始图像的预处理工作，确定其中的人脸关键点，根据预期尺寸获取对应大小的人脸图像。其次是人脸特征提取模块，此模块主要用于特征提取的具体过程，包括模型的构建与训练等过程。最后是人脸特征运用模块，此模块要考虑到具体的应用场景来设计具体的算法，例如有人脸身份识别以及验证等。

在本文中主要研究基于深度学习的人脸识别算法，相对于其他的算法，主要是在特征提取方面存在一定的差异性，其能够有效地提取人脸更本质的特征，通过此类特征的提取能够降低表情以及遮盖等因素的影响，而这也属于其明显的优势之处。因此很多学者已经开始在基于深度学习的人脸识别算法方面进行了研究和改进，使得算法效果进一步优化^[7]。

3  人脸识别算法

3.1 人脸对齐模块的算法设计

首先对人脸对齐模块算法进行设计，经过分析后本次研究中主要采用了Zhang设计的MTCNN人脸对齐算法，这种算法主要基于人脸检测与人脸对齐过程中的关联性，并设计了对应的卷积神经网络，然后通过FDDB测试集以及WIDERFACE测试集进行了算法测试，最终得到了令人满意的效果。

3.2 人脸特征提取模块的算法设计

在人脸识别算法中的核心部分是特征提取模块，也是影响最终识别效果的关键因素。在特征提取模块中，核心部分是网络模型与损失函数，通过对二者的合理设计能够提升人脸特征的提取效果，并获得更多高层本质特征，以降低外部干扰产生的影响。模型的训练过程依赖于损失函数，因此必须对损失函数进行合理地设计，这是影响人脸特征提取效果的关键因素。在设计损失函数时应该考虑到人脸基本的特征向量特性，一个是相同类内的特征差异性小，相似度高;另一个是不同类的特征相似度小，差异性大^[8]。

3.3 深度网络模型的设计

首先需要设计合理的深度网络模型，模型质量高低将会显著影响到人脸识别的性能。为了能够提取到高层的、本质的认证，则要保证特征提取模块达到更高的要求，具体是在网络模型设计与损失函数设计中保持较高的水准，由此才能降低光线、表情等因素对特征提取的影响。

经过分析，在本次研究中最终采用了选择Inception- ResNet模型，其应用的具体过程如下所示：首先对FaceID层的人脸特征维度进行设置，并得到Softmax层的神经元数目。在模型中主要含有15层，分布是卷积层、池化层、FaceID层、Softmax多分类层，其中其中卷积层、池化层主要为前13层，并交替出现，而最后两层分别是FaceID层、Softmax多分类层。在本次研究中的前13层采用了Inception- ResNet取代。

3.4模型损失函数的设计

损失函数是影响特征提取效果的重要因素，在模型训练过程中，力求得到损失函数最大或者最小时的参数，以此作为最佳的参数。在网络训练前首先要选择合适的损失函数，并将其应用到对类间、类内差异性的控制中。

为了描述特征的差异性，则一般采用距离度量的方式，即根据特征之间的距离来分析其相似度，最终在相同的类中都是相似度较高的特征，而不同类的特征相似度较小。常用的度量距离包括L2/L1范式距离、欧氏距离、马氏距离、余弦距离等，其中L2范式距离已经较多的应用到了人脸识别以及聚类等领域中，因此在本次研究中直接采用了L2范式距离来提取人脸识别的特征。

对于类间差异最大化来说，能够达到较高的人脸区分性，从而识别不同的人脸特征;类内差异最小化则指的是在相同环境中的特征相似度描述更准确，综合两种方法提升了人脸识别的精度。另外考虑到人脸特征匹配的效率问题，还应该具备紧凑性、稀疏性特征，所以必须保证损失函数的合理性，使其在特征提取中达到更佳的效果。目前常用的损失函数包括Softmax函数、Triplets Loss等。

对于Softmax多分类损失函数来说，将其应用到人脸特征提取时，能够保证各个人脸图像特征的差异性最大化，以此提高對不同人脸识别的准确性。在对人脸图像进行判定时，可以通过人脸验证方法分析各个人脸图像是否属于相同的人，在这个过程中需要通过人脸验证监督信号来对网络参数学习过程进行调节，添加验证监督信号后有助于降低特征的类内差异性^[9]。

3.4.1  Softmax损失

在本次研究中主要采用了SoftmaxLoss函数，即在网络中添加一个新的Softmax分类器层，以此提升模型参数的训练效果，有助于实现类间差异的最大化。

目前在多分类问题中已经普遍采用了Softmax Loss函数，多分类问题的类标签y取值类型较多。已知训练集的样本数目为m，具体是，输入特征，特征向量x维度大小是n+1，其中x₀=1时即为截距项，。

如果已知输入x，函数对于不同类别j的概率值表示为，因此可以假定函数输出属于k维向量代表k个估计的概率值，对应的元素总和等于1。具体如下所示：

（31）

公式中均为模型参数。考虑到计算的方便性，可以直接采用矩阵形式表示θ，其大小是K×（n+1），矩阵具体的形式如下所示：

（32）

根据函数，得到基于对数似然的损失函，其形式如下所示：

（33）

在公式中，。

为了求解的最小化问题，选择使用迭代方法求解，由此将其梯度公式表示为：

（34）

迭代的方式如下所示：

（35）

一般要将权重衰退添加到代价函数中，以此更好的解决冗余参数集的问题，此时的代价函数如下所示：

（36）

添加權重衰退之后，能够保证代价函数的解是唯一的。此时的梯度函数形式如下所示：

（37）

3.4.2  验证损失

在特征提取的过程中要利用到验证信号，其主要用于对特征距离进行监督，具体是监督多个个体图像特征间的最大距离，相同个体图像特征间的最小距离，当前在度量特征间距离的方法有多种，例如有欧式距离、L2范式距离等，在本次研究中最终采用了L2范式距离。

这里主要使用了描述特征提取的过程，代表的是特征提取函数，原始输入图像即为x，表示网络参数，表示人脸特征层输出。

所以可以将验证信号表示为：

（38）

公式中、-1时分别代表属于相同个体与不同个体两种情况。表示学习参数，在设置时需要保证样本达到最小的验证误差，只要个体间的特征向量距离不等于阈值m，则不会形成损失值;而相同个体的特征向量距离都是损失值。

另外基于余弦距离的人脸验证监督信号如下所示：

（39）

公式中，表示学习参数，σ表示sigmoid激活函数。

4  人臉验证算法设计

在提取特征之后需要继续进行人脸验证的过程，此过程依赖于合理的验证算法，可以确定人脸图像是否来自于相同的个体。但是在实际应用中，验证算法并不是固定的，而是应该考虑到不同的人脸特征属性进行设计，并形成适用性不同的验证算法。在距离度量方面可以采用范式距离或者是其他距离，以此评价特征向量的差异性，此时可以直接设置对应距离的阈值，并完成人脸验证的过程。目前常用的度量距离主要包括Ll范式距离、L2范式距离、余弦距离等类型，而在实际应用中应该综合考虑到损失函数的形式等因素，据此选择最合适的距离度量策略。在实际应用中通过需要先通过PCA实现降维，接着利用SVM或者是加权卡方距离等完成分类的过程^[10]。

经过上述处理过程后，可以将人脸特征x划分为两部分，具体公式表示为：

（40）

其中μ表示内部本质变量，并且有，ε代表外部的差异性变量，并且有。所以联合贝叶斯的联合概率分别表示为、，其高斯分布方差矩阵如下所示：

和

（41）

根据公式（41）可以计算出人脸验证的概率值。

（42）

加权卡方距离x²的公式如下所示

（43）

公式中的代表权重值，一般利用线性SVM方法计算。

另外还可以采用加权L1距离、余弦距离两种计算策略，

在本文的人脸验证中，主要采用了L2距离阈值的方法实现，其公式如下所示。

（44）

5  结语

目前人脸识别技术已经得到了较多的应用，包括在安检工作、金融工作以及交通等领域中，其稳定性强、识别精度高，市场应用前景广阔，能够为用户信息的识别提供更便捷的服务。

参考文献

• 陆化普. 智能交通系統主要技术的发展[J]. 科技导报， 2019， 37（06）： 27-35.
  • 田会娟， 刘欢， 郝甜甜， 张辉. 基于视觉舒适度的LED背光显示器最优亮度控制模型[J]. 天津工业大学学报， 2019，
  • 38（1）： 83-88.

• 陈凤萍， 齐建华. 旋转不变纹理特征在图像模式识别中应用仿真[J]. 计算机仿真， 2019， 36（2）： 353-356.
• 翟正利， 梁振明， 周炜， 孙霞. 变分自编码器模型综述[J]. 计算机工程与应用， 2019， 55（3）： 1-9.
• 刘建伯， 娄洪亮. 基于改进LeNet-5的油井井号识别方法[J]. 自动化技术与应用， 2019， 38（1）： 75-80.
• 黄佳男. 机器人表情识别与模拟研究[D]. 浙江大学， 2019.
• 徐静妹， 李雷. 基于稀疏表示和支持向量机的人脸识别算法[J]. 计算机技术与发展， 2018， 28（2）： 59-63.
• Zhendong Wu， Zipeng Yu， Jie Yuan， Jianwu Zhang. A twice face recognition algorithm[J]. Soft Computing， 2016， 20（3）.
• YILihamu YAErmaimaiti. A new Uyghur face recognition algorithm[J]. Journal of Interdisciplinary Mathematics， 2018， 21（5）.
• 张嘉凯， 杨成， 刘里. 基于文本CNN的电影推荐系统的研究与实现[J]. 软件， 2019， 40（3）： 18-25.
• 邢益良. 一种基于SL4A的智能卧室门系统[J]. 软件， 2019， 40（3）： 34-37.