基于Android的平滑折线图组件的设计与实现

2019-11-14高毅丁勇涂小琴张春红

软件 2019年9期

高毅丁勇涂小琴张春红

摘要：平滑折线图是最为常用的图表组件，Android系统并没有提供，而第三方的技术又不够成熟，本文提出了一种基于Android的平滑折线图组件的实现方法，从布局空间设计、绘制点标志、折线图平滑化、关键代码等方面对平滑折线图组件的设计实现过程进行了详细描述。该组件实验效果良好，布局合理，使用方便，支持自定义，用户体验好，能满足大多数Android应用开发的需求，有很好的实际应用价值和创新性。

关键词： Android;平滑折线图;贝塞尔曲线;数据可视化

中图分类号： TP317 文献标识码： A DOI：10.3969/j.issn.1003-6970.2019.09.003

本文著录格式：高毅，丁勇，涂小琴，等. 基于Android的平滑折线图组件的设计与实现[J]. 软件，2019，40（9）：13-17

Design and Implementation of Smooth Line Chart Component Based on Android

GAO Yi， DING Yong， TU Xiao-qin， ZHANG Chun-hong

（College of Arts and Sciences， Yunnan Normal University， Kunming 650222， China）

【Abstract】： The smooth line chart is the most commonly used chart component. The Android system does not provide it， and the third-party technology is not mature enough. This paper proposes an Android-based smooth line chart component implementation method.The design and implementation process of the smooth line graph component is described in detail in layout space design， drawing point mark， the smoothing of the line graph ， key codes and so on. The component has good experimental results， reasonable layout， convenient use， support for customization， good user experience， and can meet the needs of most Android application development， and has good practical application value and innovation.

【Key words】： Android; Smooth line chart; Bezier curve; Data visualization

0 引言

开发Android应用程序，离不开界面设计，虽然Android系统本身提供了很多组件，如：文本框、编辑框、按钮、单选按钮与单选按钮组、复选框、图片框、下拉列表框、列表框、开关按钮等，这些组件基本上能满足大多数应用的开发需求。统计图表是最早的数据可视化形式，作为基本的可视化元素仍然被非常廣泛地使用^[1]。而平滑折线图作为最为常用的统计图表之一，但Android系统本身并不提供，因此需要开发者来创建自定义的平滑折线图组件，以实现用户的特殊需求。然而，Android系统

中的平滑折线图组件的开源方案并不多，第三方的平滑折线图组件技术又不够成熟，要么使用不便，要么不够灵活，要么用户体验差。本文通过设计一个基于Android的平滑折线图组件，实现了数据的可视化展示，该组件使用灵活方便、用户体验好。下面从布局空间设计、绘制点标志、折线图平滑化、关键代码等方面对平滑折线图组件的设计实现过程做详细描述。

1 相关概念

1.1 平滑折线图

折线图是用折线（直线）把相邻的数据点连接起来，用于显示数据在一个连续的时间间隔或者时间跨度上的变化，它的特点是反映事物随时间或有序类别而变化的趋势^[2]。

平滑折线图是在折线图的基础上改进的，用平滑的曲线代替折线来连接相邻的数据点^[3]。在平滑折线图中，数据是递增还是递减、增减的速率、增减的规律（周期性、螺旋性等）、峰值等特征都可以清晰地反映出来。所以，平滑折线图常用来分析数据随时间的变化趋势，也可用来分析多组数据随时间变化的相互作用和相互影响。

1.2View

Android应用的绝大部分UI组件都放在android.widget包及其子包、android.view包及其子包中，Android应用的所有UI组件都继承了View类，View组件非常类似于Swing编程的JPanel，它代表一个空白的矩形区域^[4]。

基于Android UI组件的实现原理，开发者完全可以开发出项目定制的组件，当Android系统提供的UI组件不足以满足需求时，可以通过继承View来派生自定义组件。过程为，首先定义一个继承View基类的子类，然后重写View类的一个或多个方法来实现。

1.3Path类

在进行画线等操作时还需要连接路径，这个工具由Path提供，Path类中包含一些直线或曲线连接到指定点的方法。Android提供的Path是一个非常有用的类，它可以预先在View上将N个点连成一条“路径”，然后调用Canvas的drawPath方法即可沿着路径绘制图形^[5]。

2 关键技术

2.1布局空间设计

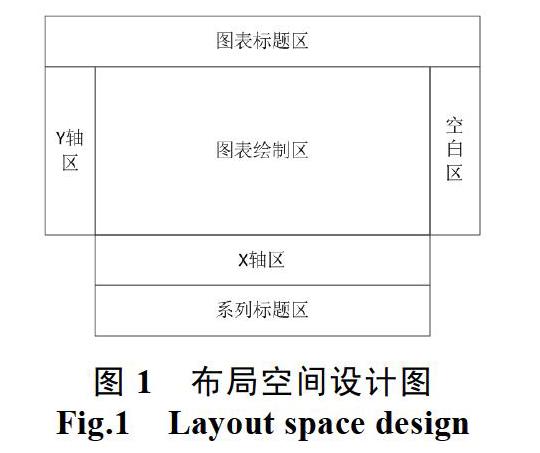
移动端应用开发最大的特点之一就是可用显示空间小，要让有限的布局空间去展示更多数据和信息，所以平滑折线图组件的布局空间设计尤为关键。平滑折线图的布局空间设计如图1所示，由图表标题区、Y轴区、X轴区、空白区、系列标题区和图表绘制区组成^[6^-^7]，其中空白区并不绘制内容，为了在水平方向上对称，它的大小和Y轴区大小一致。在该组件的设计过程中，为了能让Android应用开发者可以自由地去设置文本的大小，首先计算该组件在移动设备端的显示大小，再计算Y轴区、X轴区、空白区、系列标题区所占大小，最后得到图表绘制区的大小。下面就计算过程做详细描述，单位都为像素（px）。

（1）计算平滑折线图组件在移动设备端显示的大小

用W表示平滑折线图组件在移动端设备上所占的宽度，H表示平滑折线图组件在移动端设备上所占的高度。通过重写View类中的onMeasure方法来实现对W和H的计算。关键代码如下：

//计算显示模式

int specMode=MeasureSpec.getMode （width Me asure Spec）;

//计算宽度

int width=MeasureSpec.getSize （widthMe a su reSpec）;

//若显示模式是不确定的值，或者未指定尺寸，设置一个200的默认值

if （specMode==MeasureSpec.UNSPECIFIED）

{

width=200;

}

//计算高度的代码和上面计算宽度的代码类似，在此省略

……

setMeasuredDimension（width， height）;

编写好上面的onMeasure方法后，就可以通过以下公式来计算W和H。

W=getMeasuredWidth（） （1）

H=getMeasuredHeight（） （2）

（2）计算图表标题区、Y轴区、X轴区、系列标题区的大小

为了计算图表标题区、Y轴区、X轴区、系列标题区所占空间的宽和高，特地编写了private Rect getTextRect（String text，float textSize）方法，该方法有两个参数，第一个参数text是显示文本的内容，第2个参数textSize是显示文本的大小，返回值是Rect类型的对象。由于中文的基线和英文的基线不一样，为了顯示效果，在计算文本所占矩形时做了修正。关键代码如下：

……

Paint.FontMetricsInt fm=paint. getFont Met ricsInt（）;

//修正上边界，减去文本大小的四分之一

int top=baseLineY+fm.top-（int）（textSize/4.0f）;

//修正下边界，加上文本大小的四分之一

int bottom=baseLineY+fm.bottom+（int）（te x t Size/4.0f）;

//计算文本所占矩形空间的宽度

int width=（int）paint.measureText（text）;

Rect rect=new Rect（baseLineX，top，baseLi n e X+width，bottom）;

……

编写好上面的getTextRect方法后，就可以计算图表标题区、Y轴区、X轴区、系列标题区所占空间的宽和高。

① 图表标题区的宽W_T和高H_T计算公式如下：

W_T=getTextRect（图表标题文本内容，图表标题文本大小）.width（）（3）

H_T=getTextRect（图表标题文本内容，图表标题文本大小）.height（）（4）

② Y轴区的宽W_Y和高H_Y计算公式如下：

W_Y=getTextRect（Y轴刻度值文本内容，Y轴刻度值文本大小）.width（）（5）

H_Y=getTextRect（Y轴刻度值文本内容，Y轴刻度值文本大小）.height（）（6）

③ X轴区的宽W_T和高H_T计算公式如下：

W_X= getTextRect（X轴刻度值文本内容，X轴刻度值文本大小）.width（） （7）

H_X=getTextRect（X轴刻度值文本内容，X轴刻度值文本大小）.height（）（8）

④ 系列标题区的宽W_T和高H_T计算公式如下：

W_ST=getTextRect（系列标题文本内容，系列标题文本大小）.width（）（9）

H_ST=getTextRect（系列标题文本内容，系列标题文本大小）.height（）（10）

（3）計算图表绘制区的大小

图表绘制区的宽W_C和高H_C计算公式如下：

W_C=W–W_Y–W_Y（11）

H_C=H–H_T–H_X–H_ST（12）

2.2绘制点标志

本文实现的平滑折线图组件支持显示多个系列值，为了区别不同的系列，不仅使用了不同的颜色标识不同的曲线，还使用了不同的形状标志标识数据点。本文的平滑折线图组件支持的数据点标志有8种，分别为圆形、正方形、等边三角形、菱形、正五边形、正六边形、十字形状和五角星形。

在点标志绘制过程中，圆形、正方形、菱形、正六边形、十字形状的绘制相对简单。而等边三角形、正五边形和五角星形3种点标志的绘制相对复杂，需要用到Android中的Path方面的技术。为了方便控制点标志的位置和大小，点标志是在一个圆心点坐标为（centerX， centerY）、半径为width/2的圆内进行绘制。下面就这3种点标志的绘制过程做详细描述。

下面3种点标志的设计如图2所示，Android中canvas的绘图坐标和数学的平面直角坐标不同，向右代表X轴的正方向，向下代表Y轴的正方向。

（1）等边三角形

等边三角形的绘制是在圆心为（centerX， centerY）、半径为width/2的圆内进行的，也就是要在圆的边上确定三个点，使这三个点能够形成等边三角形。如图2（左）描述，这三个点分别为P0、P1、P2，根据三角函数可以计算出它们的坐标：

P0（centerX， centerY-width/2）

P1（centerX+（width/2）*cos（30）， centerY+（width/2）*sin（30））

P2（centerX-（width/2）*cos（30）， centerY+（width/2）*sin（30））

再把这三个点依次连接到Path对象中并形成闭环，通过绘制Path对象就可以实现等边三角形的绘制。

（2）正五边形

正五边形的绘制是在圆心为（centerX， centerY）、半径为width/2的圆内进行的，也就是要在圆的边上确定五个点，使这五个点能够形成正五边形。如图2（中）描述，这五个点分别为P0、P1、P2、P3、P4，根据三角函数可以计算出它们的坐标：

P0（centerX， centerY-width/2）

P1（centerX+（width/2）*cos（18）， center-（width/2）*sin（18））

P2（centerX+（width/2）*cos（54）， center+（width/2）*sin（54））

P3（centerX-（width/2）*cos（54）， center+（width/2）*sin（54））

P4（centerX-（width/2）*cos（18）， center-（width/2）*sin（18））

再把这五个点依次连接到Path对象中并形成闭环，通过绘制Path对象就可以实现正五边形的绘制。

（3）五角星形

五角星形的绘制是在圆心为（centerX， centerY）、半径为width/2的圆内进行的，也就是要在圆的边上确定五个点，使这五个点能够形成五角星形。如图2（右）描述，这五个点分别为P0、P1、P2、P3、P4，根据三角函数可以计算出它们的坐标：

P0（centerX， centerY-width/2）

P1（centerX-（width/2）*cos（54）， center+（width/2）*sin（54））

P2（centerX-（width/2）*cos（18）， center-（width/2）*sin（18））

P3（centerX+（width/2）*cos（18）， center-（width/2）*sin（18））

P4（centerX-（width/2）*cos（54）， center+（width/2）*sin（54））

再把这五个点依次连接到Path对象中并形成闭环，通过绘制Path对象就可以实现五角星形的绘制。

2.3折线图平滑化

平滑折线图是在折线图的基础上改进的，用平滑的曲线代替折线来连接相邻的数据点。本文选用3次Bezier曲线作为平滑的曲线，下面就折线图平滑化问题做详细描述。

（1）3次Bezier曲线

绘制平滑折线图相当于数学问题：在平面上存在n个数据点P_i（x_i，y_i），其中i=1，2，3，…，n。在相邻的每两个点P_i和P_i+1之间，用一条3次Bezier曲线连接。

3次Bezier曲线由4个点确定，起点P_i，终点P_i+1，在起点和终点之间还需要2个控制点。用3次Bezier曲线把相邻的两个点连接起来，需要2个控制点，平面上存在n个数据點，要把这n个数据点依次用3次Bezier曲线连接起来，共需要2*（n-1）个控制点，记为C1_i和C2_i，其中i=1，2，3，…，n-1^[8]。

绘制3次Bezier曲线最为关键的就是确定控制点。如果在各段3次Bezier曲线的接头处，只要求曲线函数式的一阶导数连续^[9]，也就是说，只要求曲线的切线斜率连续，那么，只要过每一个P_i点，分别作曲线的切线，然后把位于P_i前面的控制点C2_i-1和位于P_i后面的控制点C1_i，都取在过 P_i点所作的切线上就可以了。把过P_i点的切线方向，取为与线段P_i-1P_i+1平行的方向，得到控制点坐标。

控制点C1_i的坐标为：

C1_i（x_i+S*（x_i+1-x_i-1）， y_i+S*（y_i+1-y_i-1））

控制点C2_i的坐标为：

C2_i（x_i-S*（x_i+1-x_i-1）， y_i-S*（y_i+1-y_i-1））

其中，S是一个常量，表示平滑系数，且s∈（0， 1）。

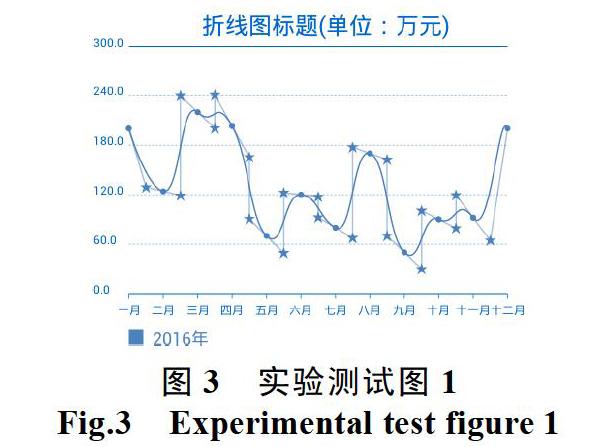
上述方法是很多应用计算3次Bezier曲线控制点的方法，使用该方法，得到实验效果如图3所示。在该图中，圆点表示数据点，五角星表示控制点，并用线条把相邻的控制点连接起来。

从图3上可以看到，第3个数据点的Y值大于第4个数据点的Y值，那么，连接这两个数据点的曲线应该是单调递减的，但实验效果并不是。还有第10个数据点到第11个数据点间的曲线应该是单调递增的，但绘制出来的效果是先递增再递减。这样的效果不能很好的表示平滑折线图的涵义，下面就控制点坐标的计算做出修正。

（2）修正控制點

把相邻的数据点用曲线连接起来，并能表示数据是递增或者递减的。为了不出现上面描述的情况，递增后递减，递减后递增。控制点的Y坐标不应超过（大于或小于）相应数据点的Y坐标，把控制点的Y坐标的值修正为相应数据点的Y坐标，得到新的控制点表示为C1_i和C2_i，其中i=1，2，3，…，n-1。

控制点C1_i的坐标为：

C1_i（x_i+S*（x_i+1-x_i-1）， y_i）

控制点C2_i的坐标为：

C2_i（x_i-S*（x_i+1-x_i-1）， y_i）

同上，S是一个常量，表示平滑系数，且s∈（0， 1）。

使用该方法，得到实验效果如图4所示。在该图中，相邻数据点间的曲线能很好的表示数据间递增或者递减的的趋势。

2.4关键代码

（1）计算控制点的关键代码如下

……

//计算控制点

for（int j=1;j

//取数据点Pi-1

PointF p0 = points.get（i）.getMyPoints（）.get（j-1）;

//取数据点Pi

PointF p = points.get（i）.getMyPoints（）.get（j）;

//取数据点Pi+1

PointF p1 = points.get（i）.getMyPoints（）.get（j+1）;

//计算控制点相对数据点Pi的X方向的偏移，平滑系数为1/8

lX = Math.abs（（p1.x-p0.x））*（1.0/8.0）;

//计算第1个控制点

float x1 = p.x + lX;

float y1 = p.y;

//计算第2个控制点

float x2 = p.x - lX;

float y2 = p.y;

//把控制点添加到动态数组中

point1.add（new PointF（x1，y1））;

point2.add（new PointF（x2，y2））;

}

……

（2）绘制平滑折线图的关键代码如下

……

//定义Path对象

linePath = new Path（）;

//设置第1个数据点为Path的起点

linePath.moveTo（points.get（i）.getMyPoints（）.get（0）.x，points.get（i）.getMyPoints（）.get（0）.y）;

//设置画笔对象的颜色属性

linePaint.setARGB（seriesItemColor.get（i%seriesItem Color.size（））.getA（），seriesItemColor.get（i%se riesItemColor.size（））.getR（），seriesItemColor.get（i% serie s ItemColor.size（））.getG（），seriesItemColor.get （i%ser ie sItemColor.size（））.getB（））;

for（int j=1;j<points.get（i）.getMyPoints（）.size（）;j++）{

//取当前要绘制的曲线的第1个控制点

float x1=point1.get（i）.getMyPoints（）.get（j-1）.x;

float y1=point1.get（i）.getMyPoints（）.get（j-1）.y;

//取当前要绘制的曲线的第2个控制点

float x2=point2.get（i）.getMyPoints（）.get（j-1）.x;

float y2=point2.get（i）.getMyPoints（）.get（j-1）.y;

//取当前要绘制的曲线的终点

float x=points.get（i）.getMyPoints（）.get（j）.x;

float y=points.get（i）.getMyPoints（）.get（j）.y;

//计算3次Bezier曲线的路径，并把此路径添加到Path对象linePath中

linePath.cubicTo（x1，y1，x2，y2，x，y）;

}

for（int j=0;j<points.get（i）.getMyPoints（）.size（）;j++）{

//绘制点标志

drawMark（canvas，seriesMark[i%seriesMark. length]，seriesItemColor.get（i%seriesItemCol or.size（）），points.get（i）.getMyPoints（）.get（j）.x， points.get（i）.getMyPoints（）.get（j）.y，dpTopx（m arkWidth））;

}

//通过Path对象linePath来实现对3次Bezier曲线的绘制

canvas.drawPath（linePath， linePaint）;

……

3 实验效果

本文实现的平滑折线图组件的实验效果如图5、图6所示，图5的平滑系数为0.25，图6的平滑系数为0.125，两个图进行对比，平滑系数小的，曲线的曲率小，更接近于直线，反之，平滑系数大的，曲线的曲率大。该平滑折线图可以显示多个系列，不同的系列，不仅曲线颜色不一样，点标志的样式也不一样，而且还具有动画效果，动画效果为依次从

左到右显示，相比现有的第三方类似的组件，具有更好的用户体验。在实际应用中，该平滑折线图还可以自定义背景颜色、背景线条粗细、背景线条颜色、文本大小、文本颜色等属性，满足了Android开发者更多的需求，显示效果的设置多样化，使用更加灵活。尽管目前也有一些基于Android的平滑折线图组件，或多或少都存在一些问题，如使用不便、不够灵活等，相比之下，本文描述的平滑折线图组件还是具有一定的实用性和创新性。

4 结语

本文提出的基于Android的平滑折线图组件可以解决一些数据展示的问题，可以展示多个系列的数据，方便不同系列的数据进行对比，能够清晰地反映出数据是递增还是递减、增减的速率、增减的规律、峰值等特征。经过测试，布局整齐，响应速度快，动画效果良好，大大增强了用户体验，能满足大多数Android应用开发人员的需求。但是，还是有一些方面需要进一步研究，如动态心电图、Bezier曲线在数据可视化中的应用等等，在下一步

的研究工作中，将在这些方面做深入研究。

参考文献

陈为，沈则潜，陶煜波. 数据可视化[M]. 北京：电子工业出版社， 2013. 12： 129.
张文彤，邝春伟. SPSS统计分析基础教程[M]. 北京市：高等教育出版社， 2011. 11： 36.
彭愿，吴阿丹，董兴鹏，李胜乐. 用JavaScript实现网页曲线图动态信息显示[J]. 软件， 2012，33（1）： 98-101.
- 李刚，疯狂Android讲义（第3版）[M]
- . 北京：电子工业出版社， 2015. 6： 123.
启舰， Android自定义控件开发入门与实践[M]. 北京：电子工业出版社， 2018. 7： 54.
高毅，王昕，杨克光. Android平台下折线图组件的研究和实现[J]. 现代计算机， 2016. 5： 69-71.
高毅，杨克光，王昕. 基于Android平台的柱状图组件的设计实现[J]. 现代计算机， 2016. 6： 77-80.
石屹，金登男. 基于塞尔曲线拟合的心电信号模式分类方法[J]. 计算机工程与设计， 2013. 4： 1437-1441.
刘成志，李军成，杨炼. 基于三次Bézier 曲线逼近的边缘亚像素定位方法[J]. 软件， 2015， 36（7）： 31-35.
李晉宏，戴海涛. 可穿戴设备数据挖掘及可视化技术的研究[J]. 软件， 2015， 36（12）： 69-71.