渗流分析中基于Signorini变分不等式结合杆单元法的排水孔模拟

曾 俊，李 星，凌晓鸣，姚孟迪，卢文由页

(1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.武汉大学水工岩石力学教育部重点实验室， 武汉430072；3.中国三峡建设管理有限公司，成都 610000)

0 引 言

在水利水电工程施工过程中，渗流问题是影响工程安全至关重要的因素之一。有限单元法是模拟渗流问题的一种有效工具，它经过多年的发展，其理论愈加成熟。固定网格有限单元法中变分不等式法以其严谨的理论基础，计算工作量小等优点得到了广泛的运用。Brezis等[1]提出了一种非线性相对较弱的扩展压力法，在一定程度上克服了最初变分不等式非线性较强的缺点；郑宏等[2]吸收初流量法的思想，将达西定律延拓至全域，建立起了有自由面稳定渗流问题的椭圆形Signorini变分不等式法，在理论上解决了出渗点的奇异性以及网格依赖性；陈益峰等[3]将郑宏所提出的方法运用于工程实际中，并引入了逐步放宽定义的自适应罚Heaviside函数替代原有罚函数，提高计算数值的稳定性的同时，确保了计算方法的鲁棒性，在诸多实际工程之中有良好的运用效果。

在实际工程措施中，为了对渗流进行有效控制，常常布置有排水孔幕等渗控措施。因此，在有限元计算过程中，能否准确地反映排水孔的渗流控制效果对工程设计以及运行都具有重要的意义。最初Fipps等[4]提出以点代孔法，但是此方法难以解决无压渗流时自由面与排水孔的界面问题。随着理论的完善，诸多学者提出了一系列更为成熟的排水孔模拟方法：杆单元法[5]、空气单元法[7]、子结构法[8]等。在上述方法中，杆单元既有较为明确的物理意义，同时不必在空间结构上反映排水孔，计算简便，经济实用，在工程计算中得到了广泛的运用。例如王建等[9]在杆单元法的基础上，进一步在地下水运动的物理意义方面进行改进，建立了汇线单元法，对于单井与复杂井群的渗流问题进行了深度剖析。

本文在稳定渗流框架下，基于含自适应罚Heaviside函数的椭圆形Signorini变分不等式，提出排水孔模拟的杆单元法。并通过一个简单模型算例，初步验证本文方法的准确性与可靠性。同时，针对实际工程的渗流问题也开展了深度分析，证明该方法在模拟含复杂排水结构的工程渗流问题中也是可靠的，进一步验证其准确性。

1 稳定渗流分析理论

1856年，法国水力学学者、工程师达西(H.Darcy)对水在均质砂槽中的流动作了一系列实验，建立了如下关系式：

(1)

假定岩土体为非均质各向异性可压缩材料，利用达西定律，则三维稳定渗流的控制方程可表示为：

(2)

式中：h=h(x,y,z)为待求水头函数；kij为渗透张量。

在实际稳定渗流问题中，针对式(2)求解，需要以下4种边界条件：

(1)水头边界条件：

(3)

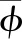
(2)流量边界条件：

(4)

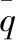
(3)出渗面Signorini型互补边界条件：

(5)

式中：Γs为潜在出渗边界。

(4)自由面边界条件：

qn|Ωw=qn|Ωd=0 (onΓf)

(6)

式中：Γf={(x,y,z)|φ=z}为自由面，即湿区与干区的分界面。

2 排水孔幕模拟方法

2.1 以管代孔

在渗流分析中，假定水流是一种连续流体，根据其连续性条件，当水流经过渗透性不同的2种材料的界面时，会产生水流的折射现象，见图1。

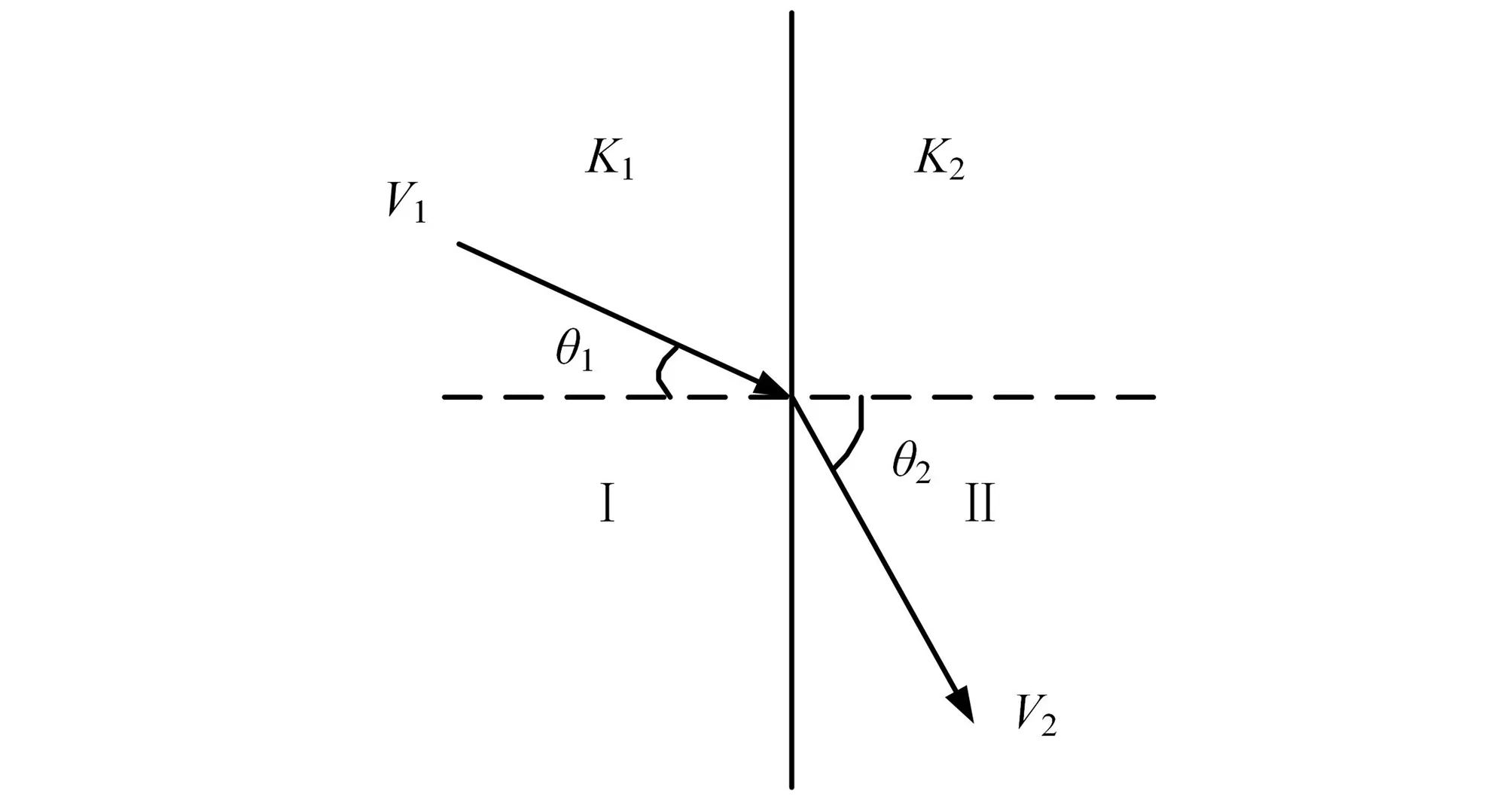
图1 渗流折射示意图Fig.1 Seepage refraction

由水流的连续性可得如下渗流的折射定律：

(7)

式中：K1、K2为介质Ⅰ、Ⅱ的渗透系数；V1、V2为水流在2介质的渗透速度，它们与界面法向夹角分别为θ1和θ2。

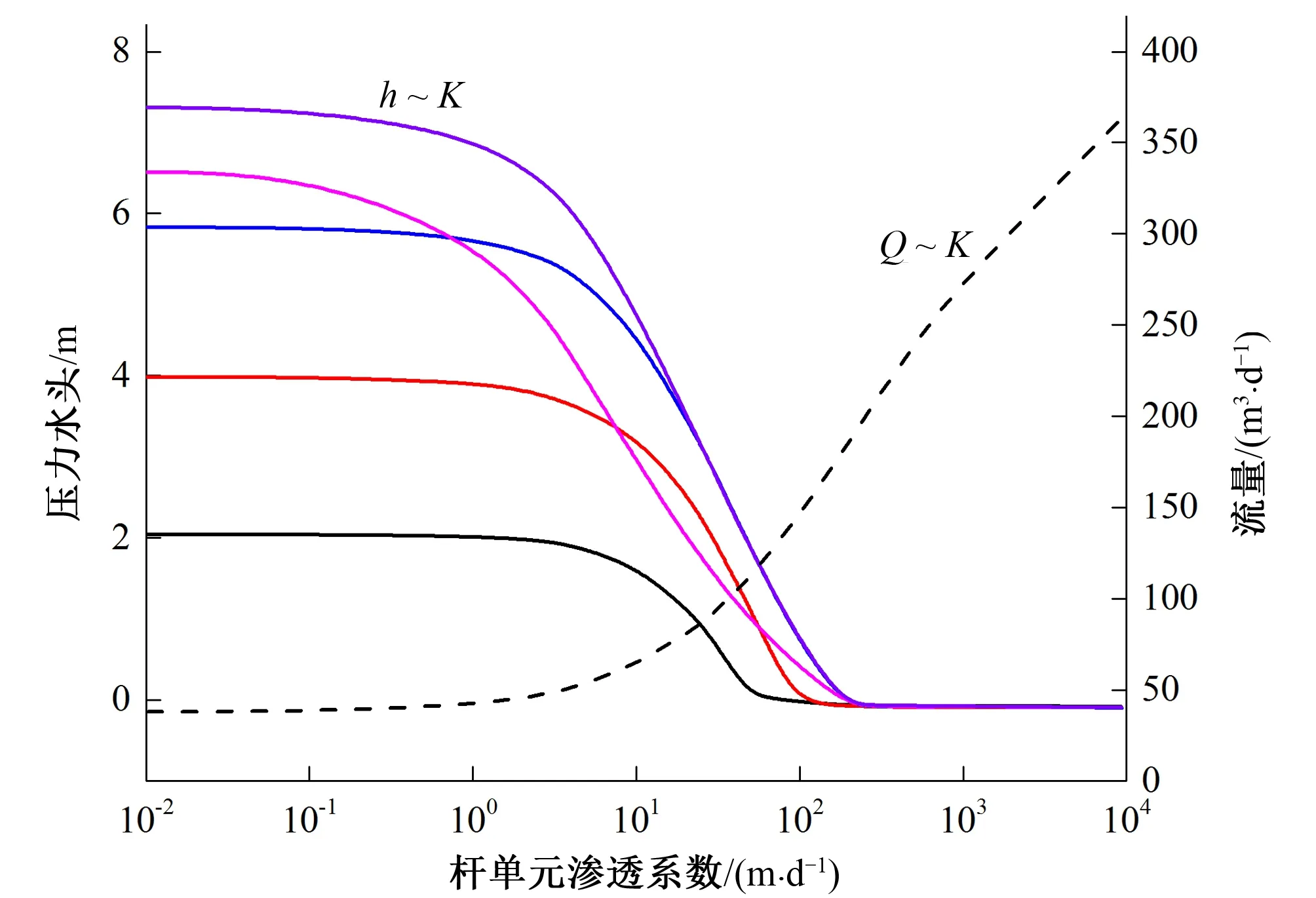
图2 孔底式排水孔 h～K、Q～K曲线Fig.2 Drop dowm type drain hole h～K、Q～K graph

图3 孔口式排水孔h～K、Q～K曲线Fig.3 Over flow type drain hole h～K、Q～K graph

2.2 杆单元法及其有限元格式

使用杆单元法模拟排水孔时，可直接利用排水孔周边岩体网格节点建立排水孔杆单元。设[Kw]为杆单元渗透矩阵，其表达形式可由下式确定：

(8)

式中：ΔF为杆单元的横截面积；ΔL0为杆单元长度；K为杆单元渗透系数，其取值按照图2、图3曲线确定。

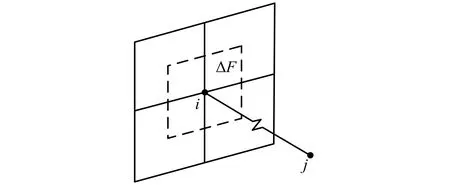
图4 杆单元示意图Fig.4 Rod drainage elements

假定一杆单元(见图4)，i,j2节点的总水头分别为Hi,Hj。除i,j2节点之外，其余各个节点的总水头矩阵为{Ha}。根据渗流控制的基本方程的有限元格式，在没有排水孔时，可以建立如下方程：

(9)

引入排水孔之后，先只需将排水孔杆单元的渗透矩阵合计入有限元网格的总渗透矩阵中，在渗流计算中，直接求解整合后的渗控方程即可。其有限元格式转变为：

(10)

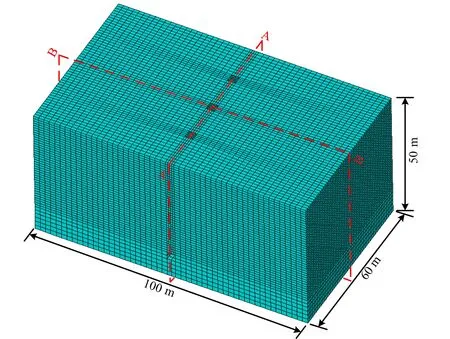
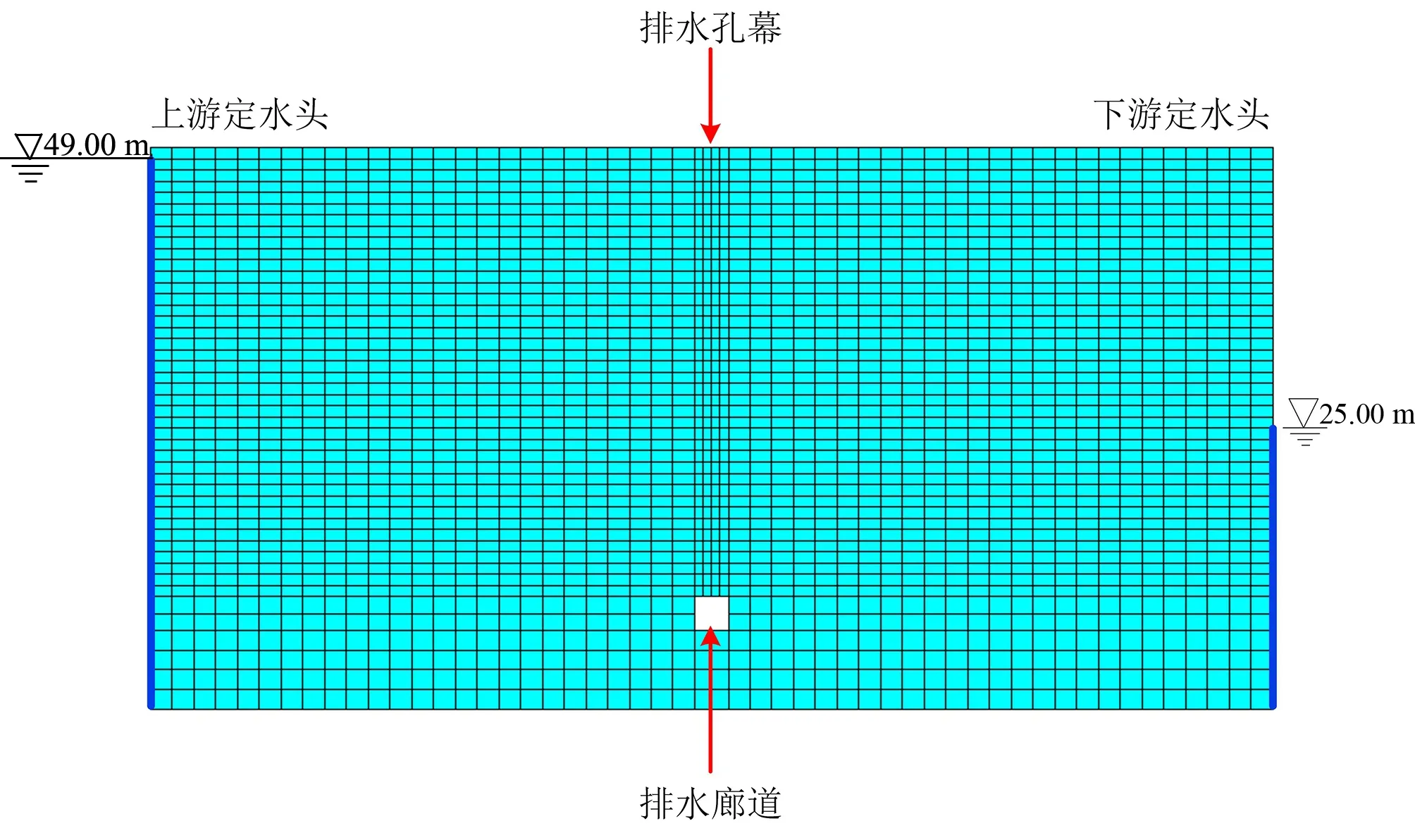
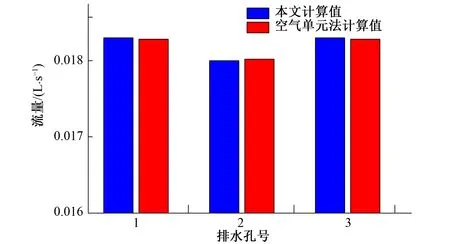
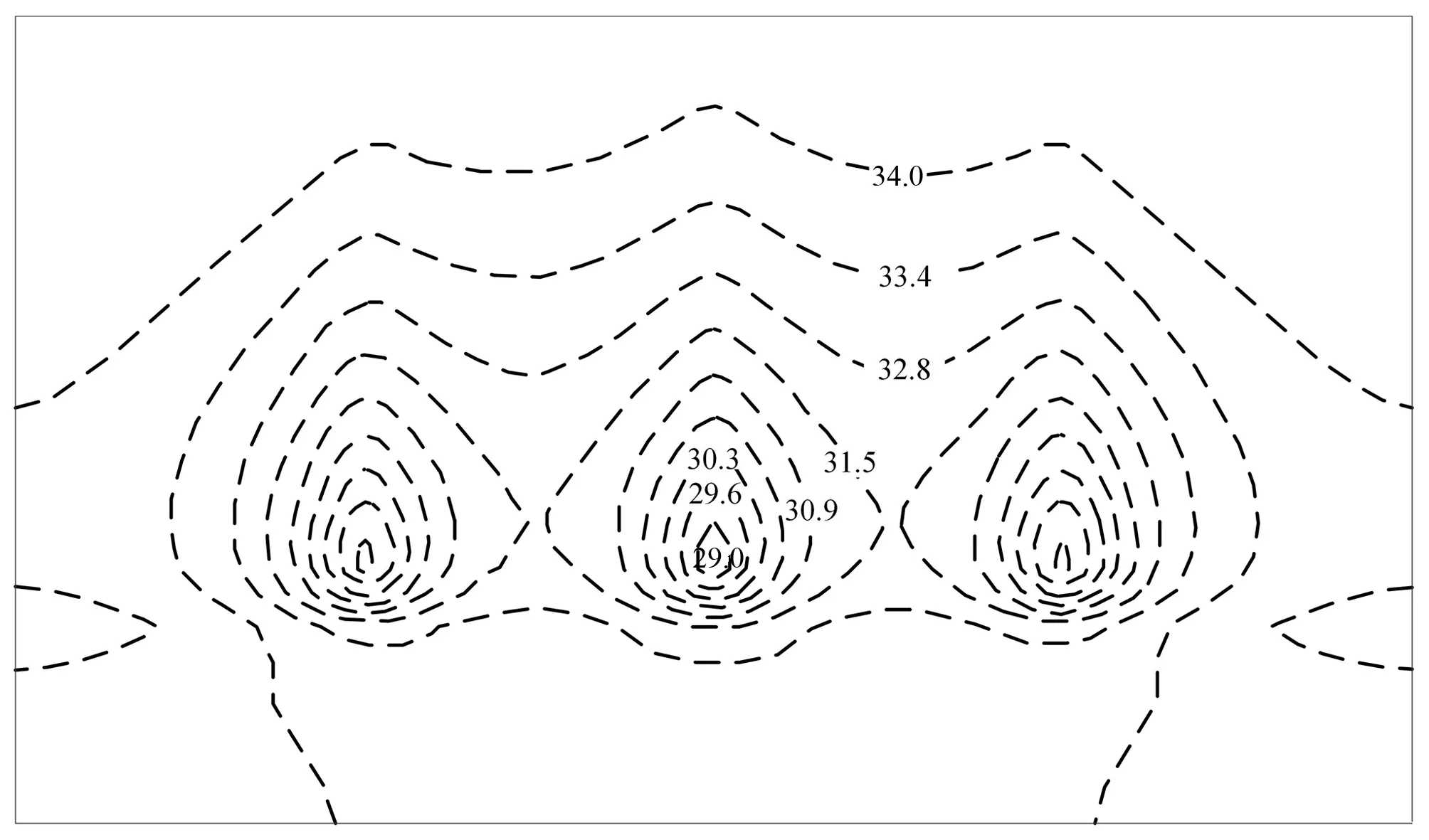
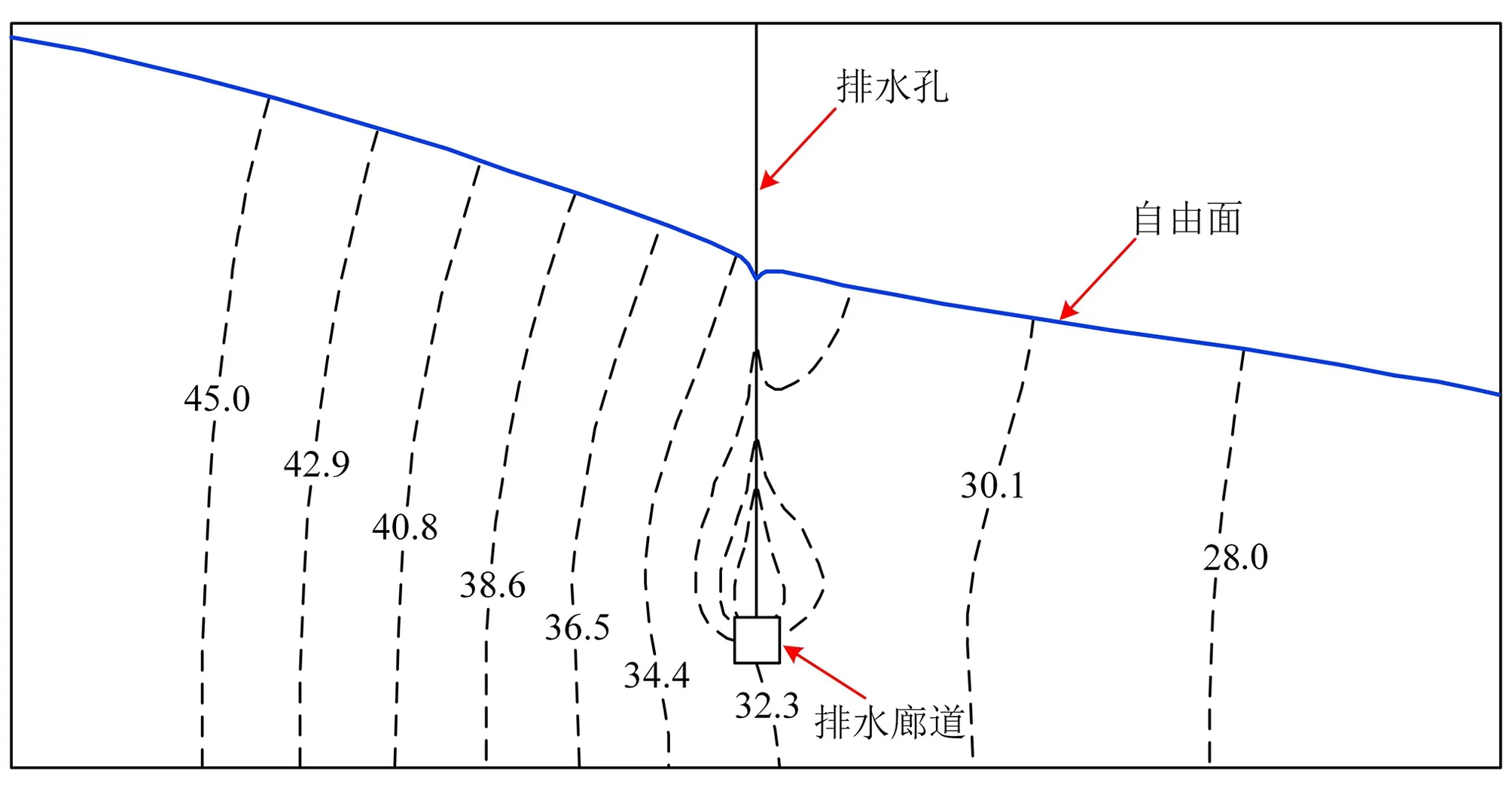
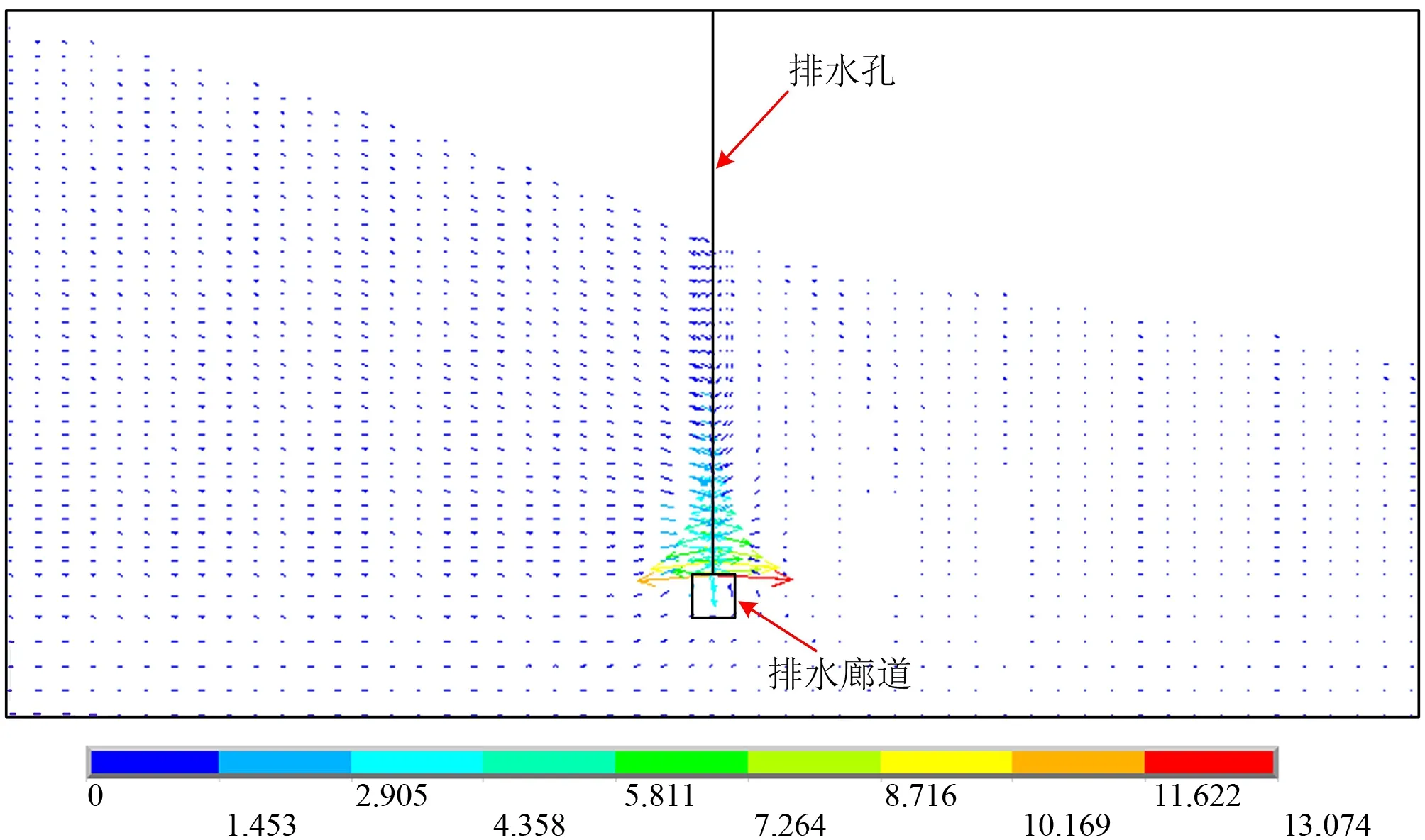
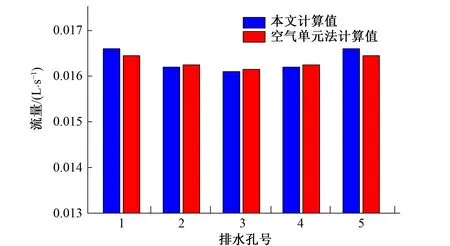
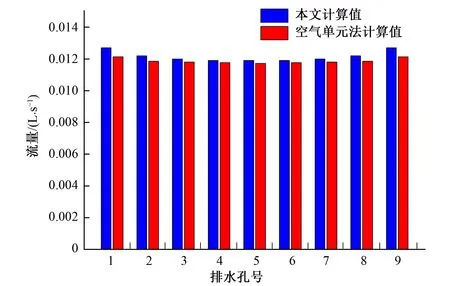
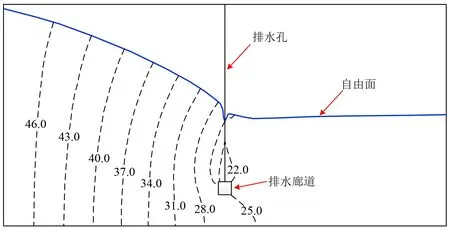
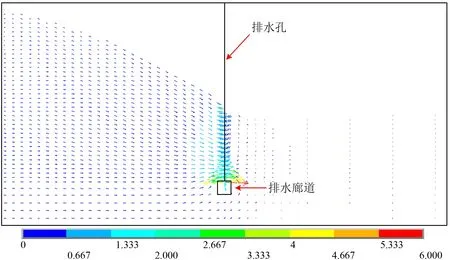
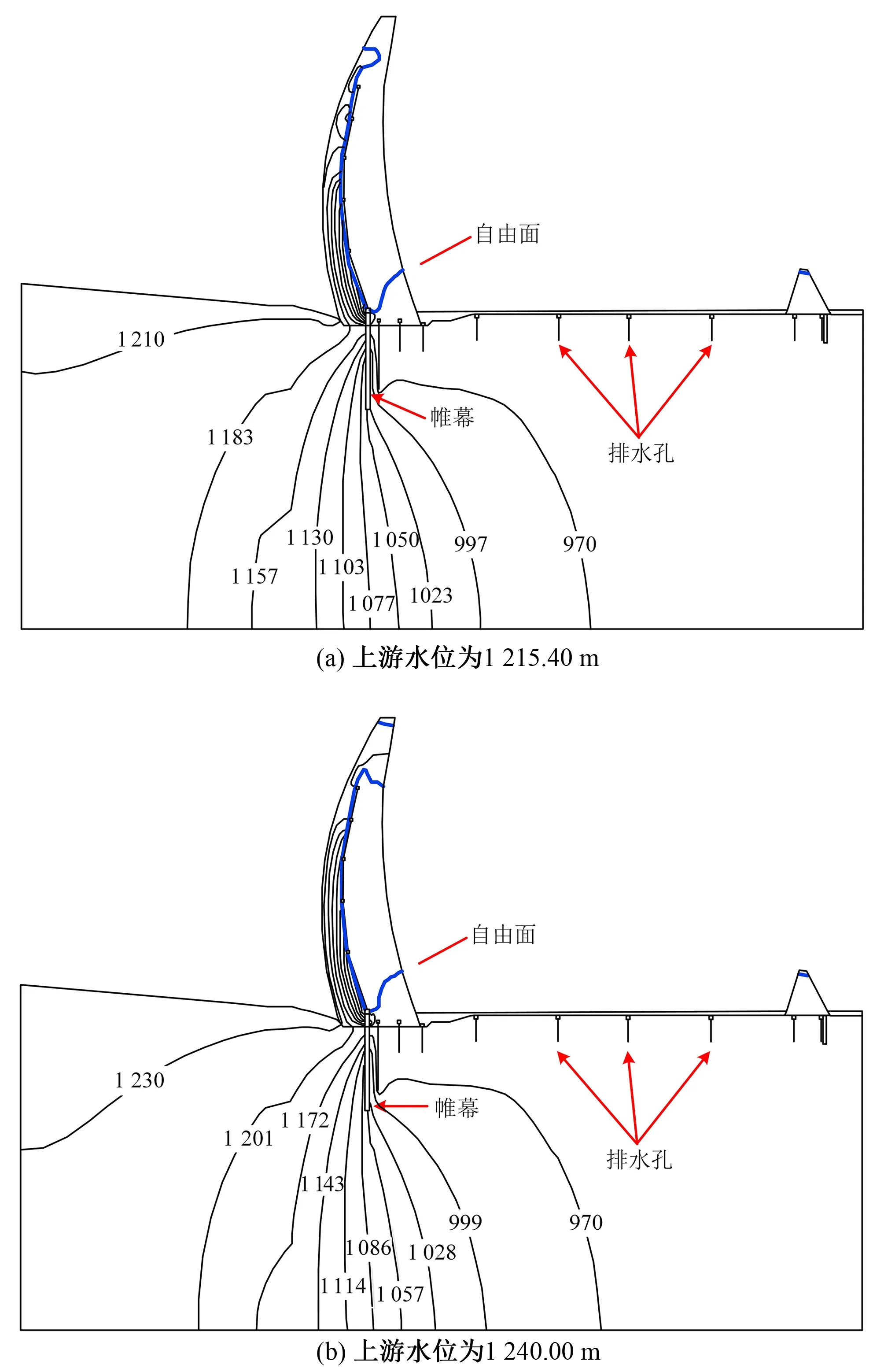
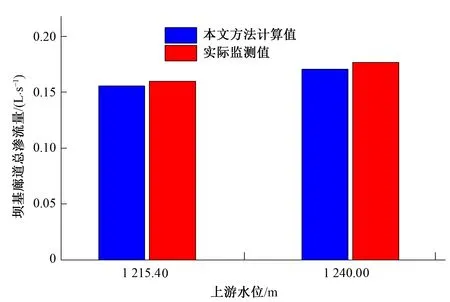
式中：λ为判定节点位置的参数；Zi为i节点的位置高程，当Hi>Zi时，节点位于自由面以上，λ=1；当Hi

3 算例验证

以含若干个排水孔的稳定渗流问题为例，验证本文方法的可靠性与准确性。计算模型见图5。岩体渗透系数K0=1×10-7m/s，排水孔渗透系数K=350K0。模型长100 m，宽60 m，高50 m。为便于全面了解和掌握模型内的渗流状况，选取2个典型剖面进行渗流计算成果的整理分析。

图5 三维计算模型示意图Fig.5 3D computing model

各典型剖面的具体位置说明如下：A-A为沿排水孔幕横剖面；B-B为模型中心纵剖面。

人人都知道“创业难，守业更难”，李志勇也不例外。随着野生菌的销量越来越可观，他也发现了很多问题，其中最显著的问题是，野生菌生长周期短，保鲜时间更短，可是用冰柜将新鲜野生菌冰冻起来，并不能解决问题，一经过冰冻的野生菌，解冻后会发生性状改变，一下锅就都软烂掉了。

模型的主要边界条件见图6，与B-B剖面垂直的2个界面取为定水头边界，上游定水头为49.00 m，下游定水头为25.00 m，其余的外部边界面为均取为隔水边界，同时排水孔于廊道溢出点取为Signorini型出渗边界。同时，由于本文仅研究排水孔幕的效果，为避免廊道取出渗边界而对排水孔出渗流量产生影响，廊道面除了与排水孔交界处取Signorini型出渗边界外，其余均取为隔水边界。

图6 三维计算模型边界条件示意图Fig.6 the boundary conditions of the 3D computing model

为了探究在不同的排水孔间距下本文方法的适用性，分别取排水孔间距为15、10、6 m 3种工况，验证上述方法的准确性与可靠性。

(1)当排水孔间距为15 m时，模型共划分单元131 336个，节点138 776个，共有排水孔3根。本文所计算的各个排水孔流量，以及同工况下邓琦[10]等使用基于弃单元网格法的空气单元法计算各排水孔所对应的流量比对结果见图7。图8为A-A横剖面等水头线分布，图9为B-B纵剖面自由面及等水头线分布，图10为B-B纵剖面渗透坡降矢量图。

图7 孔间距15 m时各孔流量比对结果Fig.7 Flow ratio comparison of each hole (hole pitch:15 m)

图8 孔间距15 m时A-A剖面等水头线分布(单位：m)Fig.8 The water head lines distribution of A-A section (hole pitch:15 m)

图9 孔间距15 m时B-B剖面自由面及等水头线分布(单位：m)Fig.9 The free surface and water head lines distribution of B-B section (hole pitch:15 m)

图10 孔间距15 m时B-B剖面渗透坡降矢量图Fig.10 The seepage gradient vector of B-B section (hole pitch:15 m)

(2)当排水孔间距为10 m时，模型共划分单元144 808个，节点153 164个，共有排水孔5根。本文所计算的各个排水孔流量，以及同工况下使用基于弃单元网格法的空气单元法计算各排水孔所对应的流量比对结果见图11。图12为A-A横剖面等水头线分布，图13为B-B纵剖面自由面及等水头线分布，图14为B-B纵剖面渗透坡降矢量图。

图11 孔间距10 m时各孔流量比对结果Fig.11 Flow ratio comparison of each hole (hole pitch:10 m)

图12 孔间距10 m时A-A剖面等水头线分布(单位：m)Fig.12 The water head lines distribution of A-A section (hole pitch:10 m)

图13 孔间距10 m时B-B剖面自由面及等水头线分布(单位：m)Fig.13 The free surface and water head lines distribution of B-B section (hole pitch:10 m)

图14 孔间距10 m时B-B剖面渗透坡降矢量图Fig.14 The seepage gradient vector of B-B section (hole pitch:10 m)

(3)当排水孔间距为6 m时，模型共划分单元155 024个，节点163 556个，共有排水孔共有9根。本文所计算的各个排水孔流量，以及同工况下使用基于弃单元网格法的空气单元法计算各排水孔所对应的流量比对结果见图15。图16为A-A横剖面等水头线分布，图17为B-B纵剖面自由面及等水头线分布，图18为B-B纵剖面渗透坡降矢量图。

图15 孔间距6 m时各孔流量比对结果Fig.15 Flow ratio comparison of each hole (hole pitch:6 m)

图16 孔间距6 m时A-A剖面等水头线分布(单位：m)Fig.16 The water head lines distribution of A-A section (hole pitch:6 m)

图17 孔间距6 m时B-B剖面自由面及等水头线分布(单位：m)Fig.17 The free surface and water head lines distribution of B-B section (hole pitch: 6 m)

图18 孔间距6 m时B-B剖面渗透坡降矢量图Fig.18 The seepage gradient vector of B-B section (hole pitch:6 m)

从上述结果分析可知，无论排水孔间距取为何值，渗流在经过排水孔幕位置处自由面均有明显下降，排水孔周边岩体形成了明显的降落漏斗，说明排水孔起到了良好的降压排水效果。各个工况下渗透坡降最大值出现在排水孔与廊道的交界面处，当排水孔间距分别为15、10、6 m时，其对应的最大渗透坡降值分别为13、7、6。说明岩体渗流确实通过排水孔幕进入到了排水廊道，排水孔发挥了其效用，说明本文所提出的模拟方法是有效的。

在同一条件下，使用基于Signorini变分不等式的杆单元法的计算流量结果与使用空气单元法进行计算的结果十分接近。当排水孔间距分别为15、10、6 m时，其最大相对偏差分别为0.11%、0.91%、4.70%。相对偏差均较小，仅当排水孔间距为6 m时相差略大。说明本文所提出的模拟方法，在各排水孔工况下均能准确模拟，适用性强、较为可靠。针对在模拟过程中所产生偏差，经过深度分析，产生这些偏差的原因有以下几点。

(1)理论基础不同。本文使用的Signorini型变分不等式法是属于固定网格法中的变分不等式法，而弃单元法属于固定网格法中的直觉化方法。直觉化方法通过自由面迭代来区分干湿区，其理论基础不同。

(2)排水孔模拟方法不同。杆单元法不能在空间构造上反映排水孔的实际布置情况，而空气单元法是对排水孔具体结构的直接模拟，在一定程度上空气单元法能够更好地还原排水孔的实际结构，其模拟结果更为精确。

(3)模型网格划分的差异。模型的网格划分往往与数值模拟计算结果有着密切联系，而在实际建模中，很难完全保证各模型网格划分与网格形态完全一致，故网格形态不一致会导致结果存在有一定的差异。

4 工程应用

小湾水电站位于云南省大理州南涧县和临沧市凤庆县的澜沧江中游，是澜沧江中下游河段8个梯级电站的第2级。工程完成蓄水后水位高程为1 215.40 m，达到正常蓄水位高程为1 240.00 m。为了验证本文方法解决实际工程中含排水孔渗流问题的实用性与可靠性，利用已有的工程资料建立小湾22号坝段的精细有限元模型，并使用本文所提出方法对该模型中132根排水孔进行模拟。模型见图19。

图19 小湾22号坝段有限元模型Fig.19 Finite element model of Xiaowan 22 dam section

模型共划分单元83 784个，节点100 839个。模型在计算过程中各个材料渗透参数取值参考文献[11]。计算过程中模型各边界条件如下：各个廊道取为Signorini型出渗边界，模型左右侧、上下游侧以及底部均取为隔水边界，拱坝后至二道坝前定水头边界取为1 004.00 m，二道坝后定水头边界取为991.09 m。同样，为了验证本文所提方法在各水头下的适用性，拱坝上游定水头根据工况不同分别取为：1 215.40 m、1 240.00 m。

图20分别为拱坝上游水位取为1 215.40、1 240.00 m之时，模型的自由面以及等水头线的分布图。图21给出了在各个工况下，流经坝体坝基廊道的渗流量的计算模拟值与实测值的对比。

图20 模型自由面与等水头线分布(单位：m)Fig.20 The free surface and water head lines distribution of model

图21 坝基底部廊道流量对比Fig.21 Flow ratio comparison of foundation gallery

对研究结果进行分析后可知，在数值计算过程中，小湾拱坝坝内排水孔将大部分坝内渗流控制在排水孔幕前，且在坝基排水孔附近形成了降落漏斗。总体而言，在计算过程中排水孔起到了良好的排水降压的作用，能够有效的控制坝区渗流场。另外，将通过坝基底部廊道的总渗流量与实际工程监测值进行对比，其相对偏差较小，相对偏差分别为2.7%、3.3%，准确性较高。通过上述分析可印证本文所提出方法在工程实例中可得到良好运用，进一步证明方法的准确性与可靠性。

5 结 论

本文通过将含自适应罚Heaviside函数的Signorini变分不等式法与杆单元法结合，提出了一种物理意义比较明确，计算收敛性好，数值稳定性强，网格依赖性小，建模以及计算工作量小的含复杂排水结构的渗流分析方法。通过对不同排水孔间距下一个简单渗流问题以及多种水位条件下小湾工程22号坝段渗流问题的模拟，验证了本文所提出方法的有效性、准确性与可靠性，为解决含有复杂排水结构的岩土体的三维渗流问题提供了一种可行方案。

□