单元式无砟轨道板间传力杆设置的计算方法

2019-11-14韦有信杨斌姜景山赵振航

中南大学学报(自然科学版) 2019年10期

韦有信，杨斌，姜景山，赵振航

(1.南京工程学院建筑工程学院，江苏南京，211167；2.中国铁路总公司工程管理中心，北京，100844；3.西南交通大学高速铁路线路工程教育部重点实验室，四川成都，610031)

单元式无砟轨道对温度变化的适应能力强[1-3]，可避免低温开裂、高温胀拱等问题的出现[4-5]，但其结构的整体性差，在列车载荷和温度作用下存在板间错台、板端翘曲等问题[6-7]，需要采用辅助的限位措施加以控制。板间传力杆设置方案是公路水泥混凝土路面常见的板端变形控制措施之一[8-9]，兰新高铁等线路借鉴该方案在单元道床板间设置了传力杆[10-11]，现场应用效果良好。公路系统中对于传力杆设置的传荷能力、布设方式及其自身性能等做了一定的研究[12-14]，但铁路系统中对于传力杆的设置研究则很少，公开文献中仅有针对某一特定设计方案的数值仿真分析[15]。为完善单元式无砟轨道板间传力杆设置的相关计算理论和设计方法，满足工程实际应用需求，本文作者以兰新高铁的传力杆设计方案为例，对传力杆设置的板端变形控制能力及其影响因素等展开分析，拟通过数值仿真和理论推导掌握板间传力杆配置的计算方法，并通过现场推板试验对研究结果进行验证。

1 传力杆设置方案

兰新高铁路基段双块式无砟轨道采用单元式结构[16-17]，其结构形式如图1所示。单元式道床板选用C40 混凝土，宽度为2 800 mm，厚度为265 mm；支承层选用C15 混凝土，宽度为3 400 mm，厚度为300 mm；单元道床板间伸缩缝宽度为20 mm。

板间设置的7 根传力杆为圆形截面的Q235 级钢棒，长度为760 mm、直径为30 mm，如图2所示[15]。传力杆两侧分别埋入道床板各370 mm，其中设置20 mm 泡沫可压缩段的一侧通过四周涂抹润滑油的方式实现与道床板的滑动摩擦接触，另一侧则不做其他处理，直接与道床板混凝土黏结为一体。

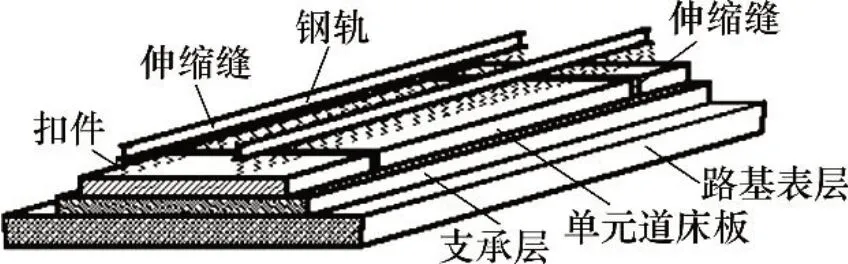
图1 单元双块式无砟轨道结构Fig.1 Structure of unit double-block ballastless track

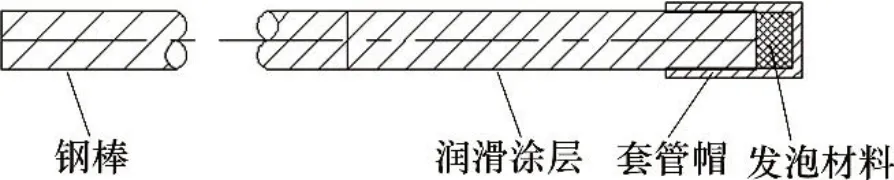
图2 传力杆结构示意图Fig.2 Structural diagram of dowel bar

2 力学模型的确定

考虑单元道床板与下部结构层层间离缝发展和变形累积等问题[18-20]，且为充分体现传力杆设置对板端变形的控制能力，力学模型中假设单元道床板与下部结构层层间完全分离，将单元道床板的整体限位措施等效为单元道床板板中横截面的完全约束。计算分析中忽略连续钢轨对道床板变形的反作用，将其视为一定的强度储备。

为正确建立理论分析模型，现首先建立数值仿真模型对板间传力杆的工作状态展开分析，板间设置7 根直径为30 mm 传力杆的6.5 m 单元道床板仿真模型如图3所示。仿真模型中传力杆左侧采用黏结接触实现与道床板的连接，右侧则采用滑动摩擦接触进行界面模拟。

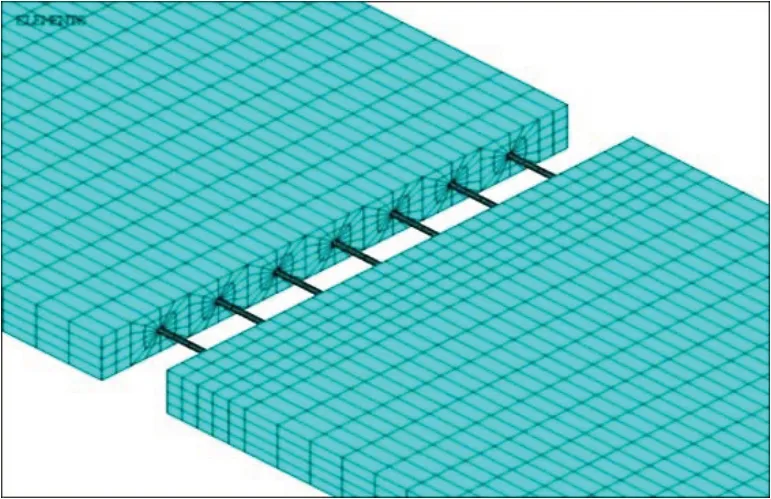
图3 传力杆设置分析的有限元模型Fig.3 Finite element model for analysis of dowel bar settings

单元道床板的板端变形主要包括列车横向荷载作用下的横向变形和温度梯度作用下的竖向翘曲2种形式，本文分析中荷载取值参照“高速铁路设计规范”，板端横向变形分析中列车轴重取值220 kN，列车横向荷载按照轴重0.8 倍计算，板端翘曲计算中选用45 ℃/m的负温度梯度。现分别对仿真模型施加列车横向荷载和温度梯度作用，其中翘曲分析中忽略单元道床板重力作用的影响，关于传力杆工作状态的部分仿真分析结果如图4所示。

图4 传力杆力学性能仿真分析Fig.4 Simulation analysis of dowel bar’s mechanical propeties

横向荷载作用下伸缩缝两侧传力杆存在明显的错位现象，说明板间传力杆承受了显著的剪力和弯矩作用；温度梯度作用下板间传力杆变形平顺，左右两侧对称，传力杆的同一横截面上下拉压应力幅值相同，说明此时板间传力杆处于纯弯矩作用下。现基于上述假设条件和分析结果，构建传力杆设置对板端变形控制能力分析的力学模型，如图5所示。图中：L为单元轨道板长度；F为列车横向荷载；Q为传力杆横截面承受的剪力；MA，MB和M′分别为不同状态下传力杆截面承受的弯矩。

板间伸缩缝范围内传力杆受力状态如图6所示。

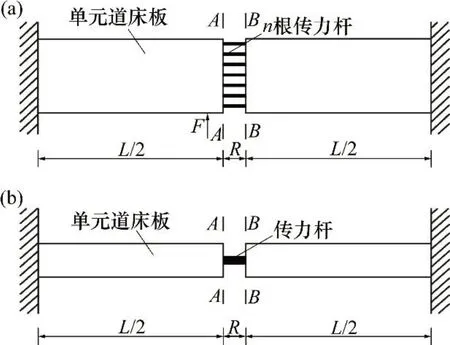
图5 力学模型Fig.5 Mechanical model

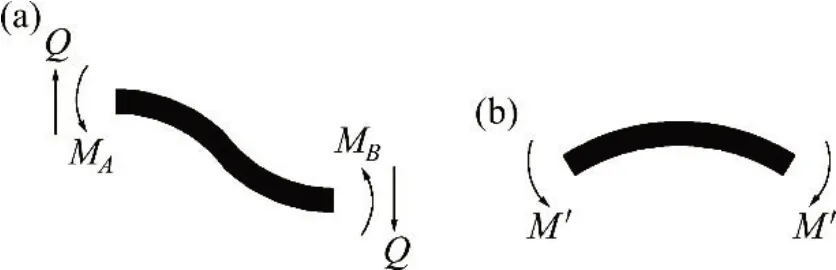
图6 板间传力杆受力示意图Fig.6 Schematic diagram of dowel bar force between plates

3 理论推导及分析

3.1 板端横向变形控制

列车横向荷载作用下结构受力形式如图7所示。

由微分原理可推算出横向荷载作用下A截面处单元道床板的横向位移ΔA和转角θA：

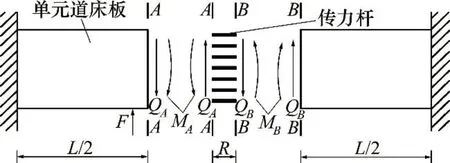
图7 横向荷载作用下结构受力示意图Fig.7 Force analysis of structure under lateral load

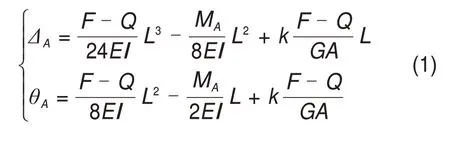
式中：k为截面剪应力分布不均匀系数；E和G分别为单元道床板混凝土弹性模量和剪切模量；A为单元道床板横断面面积；I为单元道床板横向弯曲的截面惯性矩。

同理，可推算出B截面单元道床板的横向位移和转角：

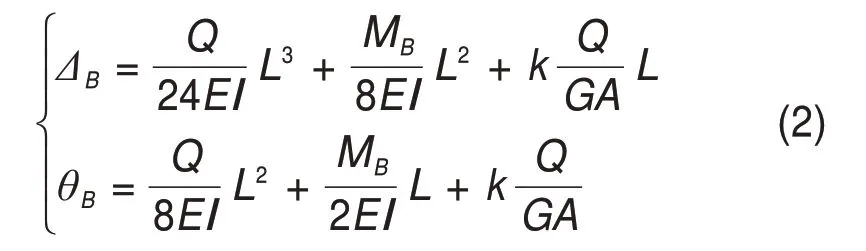
传力杆两侧A和B截面在弯剪作用下也将产生相对位移Δ和转角θ，由小变形假设的近似计算可得：

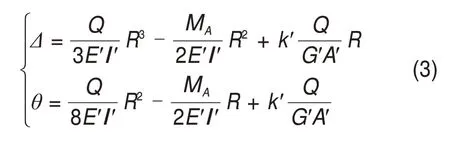
式中：Eʹ和Gʹ分别为传力杆的弹性模量和剪切模量；Iʹ和Aʹ分别为每组传力杆的截面惯性矩和截面总面积。

由小变形假设可认为A和B截面两侧道床板与传力杆变形一致，由此可建立如下近似数学关系：

同时，依据板间传力杆弯矩平衡，可建立各内力之间的数学关系：

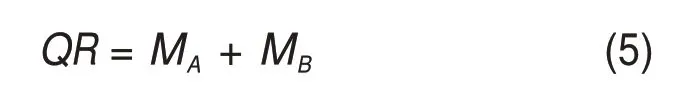
将式(1)～(3)代入式(4)，通过代换可得：

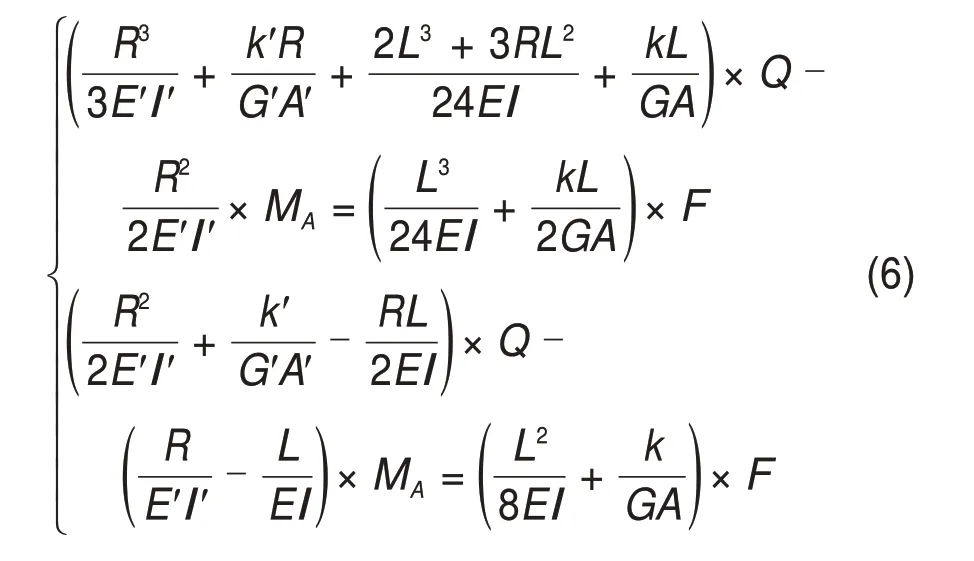
联立式(5)和(6)可求得不同传力杆配置方案对应的结构内力，进而可求得板端横向变形幅值。但该计算方法繁琐复杂，不仅不利于传力杆配置的设计计算，而且无法直观掌握影响传力杆设置效果的关键因素，现依据实际工况对计算方法进行适当简化。

首先，鉴于单元道床板板端横向变形幅值远小于单元道床板长度，其板端截面的偏转角度趋近于零，由此可认为伸缩缝宽度范围内传力杆弯矩零点位于伸缩缝中点，由传力杆零点截面弯矩平衡可得：

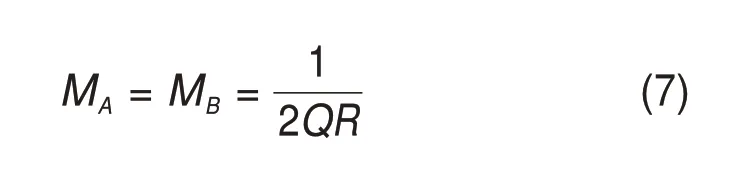
其次，板间配置4～10根直径为30 mm的传力杆时，代入数值计算可发现6.5 m单元道床板板间传力杆传递的剪力为列车横向荷载的0.471～0.495倍，伸缩缝两侧单元道床板内部剪力较为接近，二者对应的板端剪切变形差小于0.005 mm，且考虑剪切变形不引起单元道床板端面的偏转，故力学分析中忽略单元道床板剪切变形的影响，仅将其视为单元道床板板端横向变形幅值的附加组成部分。

然后，板间配置4～10根直径为30 mm的传力杆时，代入数值计算可发现20 mm 伸缩缝宽度范围内传力杆的横向剪切变形幅值小于0.01 mm，可知因传力杆剪切变形引起的两侧单元道床板剪力差值很小，故力学分析中同步忽略传力杆剪切变形的影响，亦仅将其视为伸缩缝两侧道床板端面横向位移差的附加组成部分。

最后，基于如上3个假设条件，重新开展上述公式推算，可确立板间传力杆传递的剪力Q与列车横向荷载F存在如下数学关系：

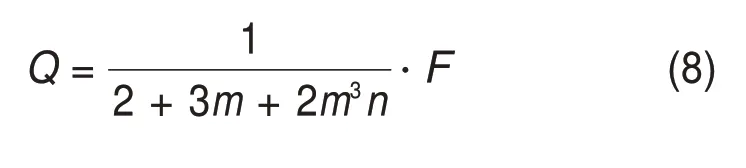
式中：m为伸缩缝宽度和单元道床板长度的比值R/L；n为单元道床板与传力杆组的横向弯曲刚度比值EI/(EʹIʹ)。随着传力杆配置数目、直径的增大，n逐渐变小，板间传力杆传递的剪力Q将逐渐增大，当n趋近于无限小时，板间传力杆传递的剪力Q存在上限值F/(2+3m)。

同理，基于如上3个假设条件，可推算出加载侧单元道床板板端横向位移Δ1和伸缩缝两侧单元道床板板端横向位移差Δ：

由式(9)和(10)可知：传力杆设置对板端横向变形的控制能力不仅与传力杆配置方案、各部件材料性能相关，还与单元道床板长度和伸缩缝宽度等结构设计因素相关，不同结构设计方案对应的传力杆设置效果也有所不同。

为更直观体现各因素影响下的板间传力杆设置效果，现代入数值展开计算分析。首先，以6.5 m 单元道床板、20 mm 伸缩缝的结构设计方案为例，对单元道床板施加板端列车横向荷载，不同传力杆配置方案对应的加载侧单元道床板板端横向变形幅值如图8所示。

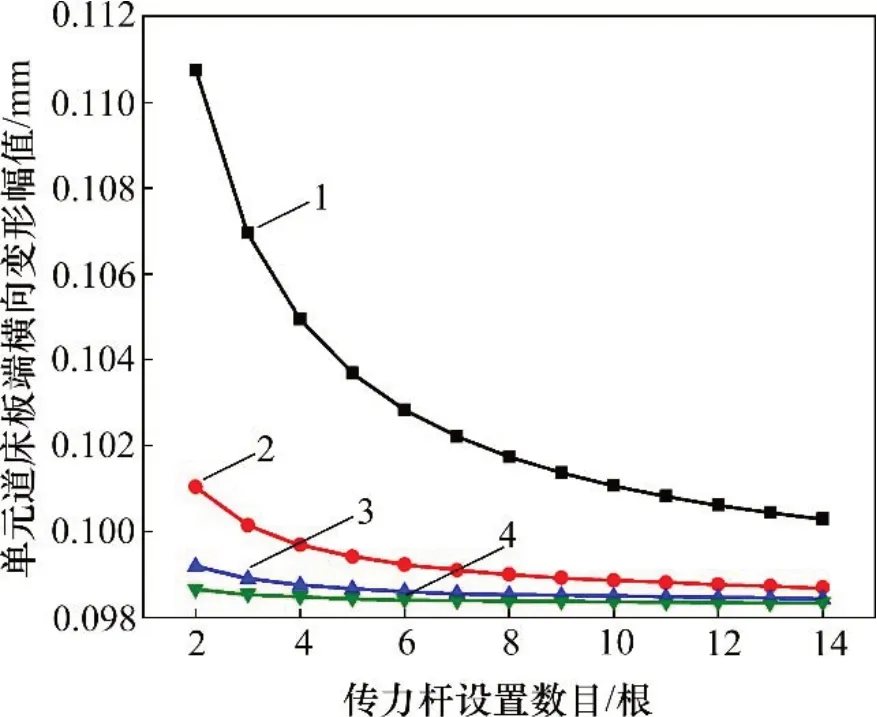
图8 单元道床板板端横向变形幅值Fig.8 Lateral deformation amplitude of unit bed slab’s end

随着传力杆设置数目、直径参数的增大，单元道床板板端横向变形幅值逐渐减小，板间横向整体性得以加强，但传力杆配置达到一定标准后，继续增大传力杆数量、直径对其提高控制板端横向变形能力的效用很小，如配置7根直径为30 mm传力杆即可降低49.5%的板端横向变形幅值，对应的板端横向变形幅值已接近极限值0.098 3 mm。在传力杆材料强度满足应力要求的前提下，过量的传力杆配置反而将给施工造成不必要的麻烦。关于传力杆应力的计算，可依据式(7)和(8)推算出传力杆内力，再按照传力杆配置情况开展强度分析，在此不再展开说明。

现以7 根直径为30 mm 的传力杆配置方案为例，判别同一传力杆配置方案在不同结构设计方案中控制板端横向变形的能力差异，分析中采用传力杆设置前后的板端变形幅值差占原有变形幅值的比例为标准来衡量不同结构设计方案中传力杆抑制板端横向变形的能力，如图9所示。

图9 传力杆抑制横向变形的能力Fig.9 Ability of dowel bar to control lateral deformation

随着单元道床板长度的增加、伸缩缝宽度的减小，同一传力杆设置方案的板端横向变形控制能力逐渐增大。结合式(8)分析，可进一步明确板间传力杆的横向变形控制能力与伸缩缝宽度和单元道床板长度的比值m密切相关，m越大，其控制能力越小。此外，不同结构设计方案中传力杆设置抑制的板端变形幅值均未能突破原有变形幅值的50%，出现该现象的原因在于传力杆无法传递纵向荷载，单元道床板自身依旧可以通过纵向的伸缩偏转变形而释放部分内力，进而在板端产生一定幅值的横向变形量。

3.2 板端竖向翘曲控制

温度梯度作用下结构受力形式如图10所示。

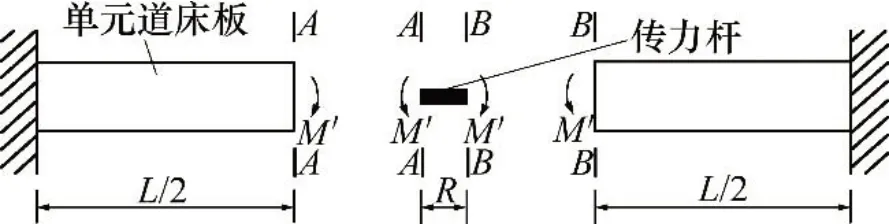
图10 温度梯度作用下结构受力分析图Fig.10 Force analysis of structure under temperature gradient

若单元道床板板端竖向翘曲受到了板间传力杆的完全抑制，则此时温度梯度S对应的弯矩Mʹ处于最大值MT状态，推算可得：

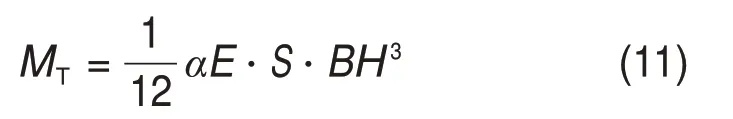
式中：α为混凝土热伸缩系数；B和H分别为道床板的宽度和厚度。

若板内翘曲应力得到全部释放，则板端竖向翘曲位移和截面转角处于最大值状态，推算可得：

板间传力杆配置情况不同，对应的结构内力也将有所不同，板内弯矩M′对应的单元道床板板端A截面竖向位移y′和转角θ′分别由下式计算可得。

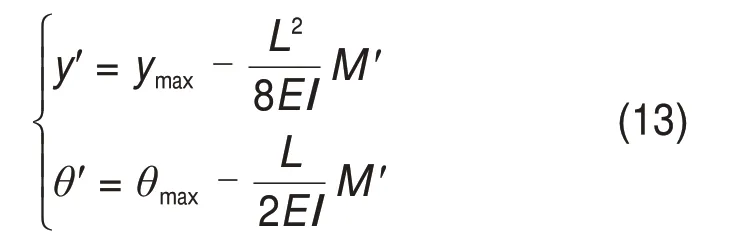
同理，可得板内弯矩M′作用下传力杆A截面的截面转角θbar：

根据A截面左右两侧道床板和传力杆转角相同，联立式(13)和(14)，可求得不同传力杆配置方案对应的板内弯矩M′：

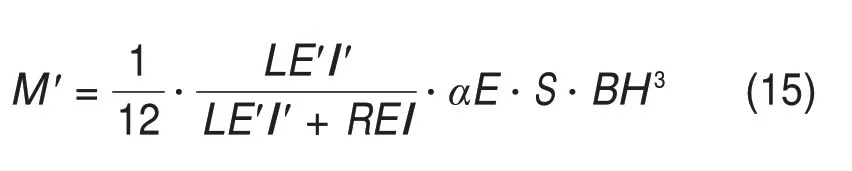
为充分体现板间传力杆设置对板端翘曲变形的控制能力，计算分析中未考虑单元道床板重力作用的影响。现采用传力杆设置前后的板端变形幅值差占原有变形幅值的比例为标准来衡量不同结构设计方案中传力杆抑制板端翘曲变形的能力，假设该比例为Z，代入上文公式计算可得：

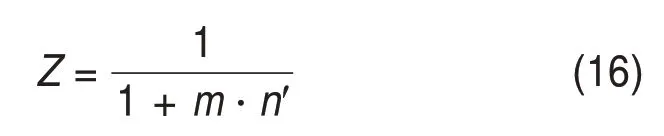
式中：n′为道床板与传力杆组的竖向抗弯刚度比值EIy/(E′I′y)。由式(16)可知：除了传力杆自身性能以外，单元道床板长度和伸缩缝宽度也是影响传力杆控制板端翘曲变形能力的重要影响因素。

为更直观体现各因素影响下的板间传力杆设置效果，现结合工程实际，代入数值展开计算分析。首先，以6.5 m单元道床板、20 mm 伸缩缝的结构设计方案为例，对其施加45 ℃/m负温度梯度作用，不同传力杆配置方案对应的板端竖向翘曲幅值如图11所示。

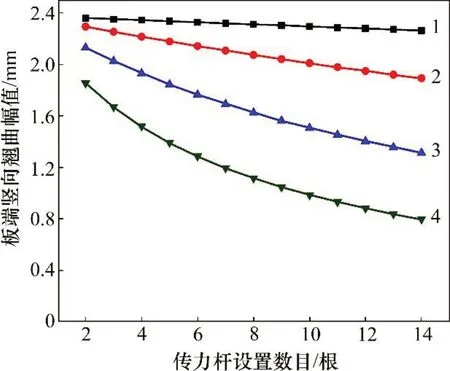
图11 单元道床板板端竖向位移Fig.11 Vertical displacement of unit bed slab’s end

随着传力杆配置数量、直径的增大，板端竖向翘曲幅值逐渐降低，传力杆配置的增加可明显提高其控制板端翘曲变形的能力，如板间配置7根直径为30 mm 传力杆可降低11.4%的板端翘曲幅值，配置8 根直径为40 mm 传力杆则可降低31.6%。对照图4的数值仿真分析可知：配置7 根直径为30 mm传力杆的6.5 m单元道床板在45 ℃/m负温度梯度作用下的板端竖向翘曲幅值为2.118 mm，与本文理论推算值2.107 mm基本一致，初步证明本文建立的传力杆配置计算方法的正确性。

现以7 根直径为30 mm 的传力杆配置方案为例，判别同一传力杆配置方案在不同结构设计方案中控制板端竖向翘曲变形能力的差异，图12所示为不同结构设计方案中该传力杆配置方案设置前后的板端翘曲变形幅值差占原有变形幅值的比例。

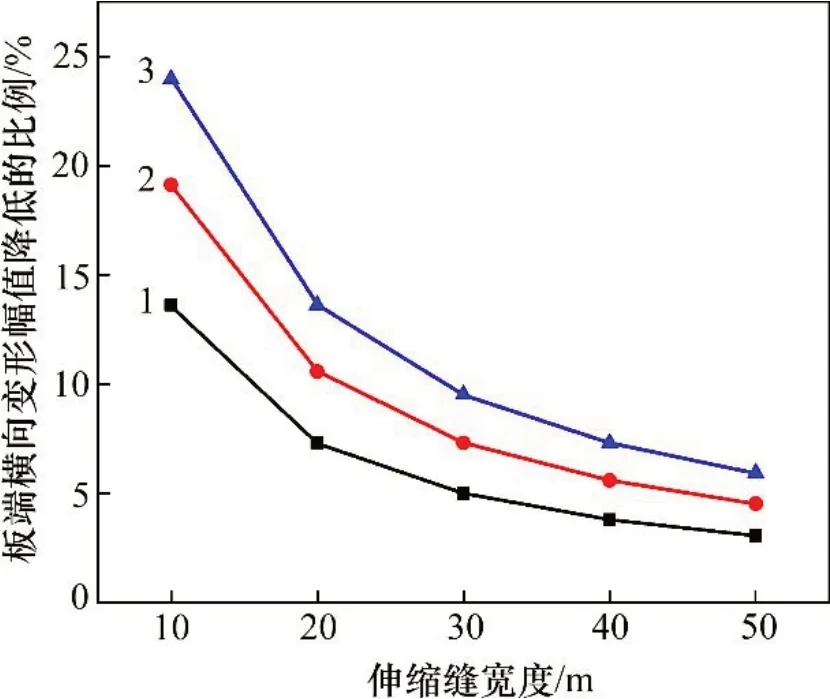
图12 传力杆抑制翘曲变形的能力Fig.12 Ability of dowel bar to control warpage deformation

伸缩缝宽度的变化对传力杆的设置效果影响显著，随着伸缩缝宽度的变大，传力杆的控制效果不断降低，原因在于伸缩缝宽度的变大将放大传力杆两侧截面的转角，降低传力杆弯曲对板端翘曲的反作用。受重力作用影响，负温度梯度作用下板端翘曲长度有限，单元道床板长度参数的影响需要结合不同结构方案中负温度梯度的翘曲影响范围进行分析，若单元道床板全长处于负温度梯度翘曲影响范围以内，则单元道床板的长度越长，传力杆设置的板端翘曲变形控制效果越好，否则单元道床板长度参数的增加对传力杆控制板端翘曲变形的能力无影响。

4 现场推板试验验证

为验证本文传力杆设置计算方法的正确性，进一步掌握传力杆设置对单元道床板结构整体性的影响，特开展现场试验段推板试验。

4.1 现场推板试验

现场试验段铺设于我国西北甘肃地区，其结构形式为采用单元道床板结构的路基段双块式无砟轨道，试验段单元道床板长度为11.7 m、伸缩缝宽度为20 mm，单元道床板间设置7 根直径为30 mm的传力杆。试验段中单元道床板的受力状态与本文力学模型基本一致：单元道床板与下部支承层间铺设了一层滑动膜，以实现二者层间分离滑动；单元道床板板中部分横向设置了一排销钉，以实现对单元道床板的整体约束。

推板试验利用线路一侧反力墙，使用千斤顶在单元道床板板端位置逐级施加横向荷载，如图13所示，并使用位移计等对单元道床板的整体变形进行了监测。考虑横向荷载较小时，支承层对道床板横向变形的摩阻效应较为明显，故试验中采用700 kN 和1 000 kN 2 个大幅值横向荷载，以便使试验状态尽可能接近最不利工况。试验过程中横向荷载首先由0 kN 逐级加载至700 kN，再逐级卸载，卸载完全后再逐级加载至1 000 kN，随后再逐级卸载，每级加减载幅值为50 和100 kN 不等，每级加减载间隔时间为10 min。

图13 单元道床板推板试验Fig.13 Push plate test of unit bed slab

4.2 试验结果及分析

板端横向荷载作用下轨道结构与路基表层黏结良好，但单元道床板与下部支承层层间滑动现象明显。基于对单元道床板左右两侧多点位的横向变形幅值监测，可掌握横向荷载作用下伸缩缝两侧单元道床板的横向变形形态。板端荷载为700和1 000 kN 时，伸缩缝两侧单元道床板的横向变形情况如图14所示。

伸缩缝两侧的单元道床板产生同向且幅值较为接近的横向位移，二者的协同变形充分说明板间传力杆的设置有效地加强单元道床板间的整体性。加载点一侧单元道床板横向变形幅值要比伸缩缝另一侧单元道床板的大，说明加载点一侧单元道床板分担的横向荷载超过50%，而板间传力杆传递的剪力小于横向荷载的50%，符合式(8)的分析结论。

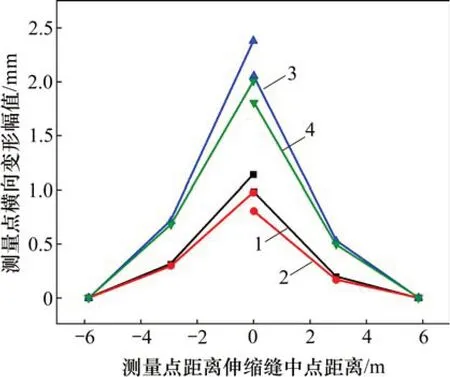
图14 单元道床板横向位移Fig.14 Transverse displacement of unit bed slab

推板试验的加减载过程中，加载侧的单元道床板板端横向变形幅值变化如图15所示。

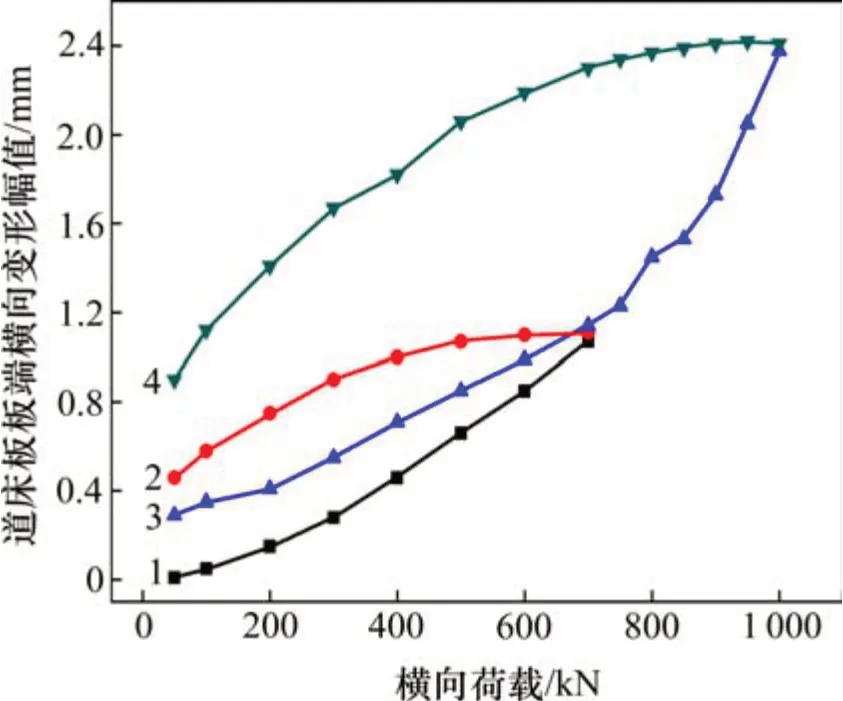
图15 板端横向位移变化曲线Fig.15 Transverse displacement curve of plate end

随着横向荷载幅值的增大，板端横向变形幅值逐渐变大，线形变化较为平缓。轨道结构处于稳定状态时，横向荷载700 kN 和1 000 kN 对应的板端横向变形实测值分别为1.14 mm 和2.38 mm，基于本文建立的计算方法可得700 kN 和1 000 kN对应的横向变形推算值为1.73 mm 和2.47 mm，对比分析可知二者的推算值均大于实测值，且1 000 kN 横向荷载的推算值与实测值非常接近，但700 kN 横向荷载的推算值与实测值幅值差占到了推算值的34%，偏差较明显，出现该现象的原因在于横向荷载越小，单元道床板的横向滑动区段越短，力学模型中忽略的支承层层间摩阻效应越大。若基于本文计算方法开展传力杆配置设计，则其板端变形幅值实际值将小于设计要求值，可有效保障传力杆设置对板端变形控制的可靠性。