横向摆动对深海采矿扬矿管输送特性的影响
2019-11-14徐海良饶星杨放琼
徐海良,饶星,杨放琼
(1.中南大学机电工程学院,湖南长沙,410083;2.中南大学高性能复杂制造国家重点实验室,湖南长沙,410083)
大洋多金属结核是一种蕴藏量丰富、开采价值大、对国防工业具有重要作用的深海矿产资源,为开采这种矿产资源,世界各国已经开发出多种采矿系统[1-3]。经过理论和实验研究,普遍认为矿浆泵水力管道提升开采系统最具工业应用前景,该系统主要包括集矿系统、扬矿子系统和水面支撑系统3 部分[4]。在复杂的海洋动力环境下,长达几千米的扬矿管道会受到波流联合作用力,产生横向摇摆,以及随采矿船做上下升沉运动。管道的复杂运动引起内部固液两相流体运动状态的改变,对管道的输送特性产生重要影响。为保证深海采矿作业的安全、高效、可靠的运行,研究海洋动力环境下深海采矿扬矿管的输送特性具有重要意义。近年来,许多学者对矿石颗粒管道水力输送问题进行了深入研究。王英杰等[5]利用高速摄影技术对水利提升管道内颗粒的运动规律进行了实验研究,得到了颗粒的运动轨迹和分布规律;黄中华等[6]通过数值仿真和理论分析相结合的方法分析了水力提升条件和系统参数对提升性能的作用规律;徐海良等[7]运用CFD技术对天然气水合物水力提升过程进行了数值分析,研究了提升系统参数对管道压力损失和颗粒分布的影响规律;BAR-AVI[8]通过实验研究了涡流作用下扬矿管内两相流的运动特征;VAN WIJK 等[9]使用流化理论分析垂直水力输送系统稳定性,通过实验证明了该理论的预测结果在一定条件符合实际情况。但是关于海洋动力环境下,横向摆动对深海采矿扬矿管输送特性的影响研究显见报道。本文作者以横向摆动工况下矿石竖直输送管道为研究对象,采用双欧拉模型和RNGk-ε湍流模型,运用Fluent动网格技术对矿石水力输送过程进行仿真分析,研究横向摆动对矿石输送管道内压力损失梯度、管道出口颗粒平均体积分数、颗粒体积分数沿径向分布以及颗粒轴向速度分布的影响规律。
1 数值模拟基础
1.1 计算模型
扬矿硬管工作于复杂的海洋环境中,会产生纵向振动和横向摆动[10-11],纵向振动可以使用附加吸振器和海面升沉补偿装置得到缓解[12]。本研究中不考虑2个方向的耦合运动,着重研究横向摆动对深海采矿扬矿管输送特性的影响。
由于深海采矿扬矿硬管一般长达数千米,本文选取管道中部的部分管道作为研究对象,且长度远远小于输送管总长度,其上各点摆动位移相对于整个管道来说可视为相同,于是可以将管道的横向摆动近似认为横向简谐振动,运动位移沿x方向一致。考虑到计算时间,根据轴对称假设将管道简化为二维计算模型,管道几何模型如图1所示。所研究管道模型的位移-时间函数和速度-时间函数分别为:

式中:s为摆动位移;v为摆动速度;t为摆动时间;A为最大摆幅;T为摆动周期。
1.2 网格划分
建立计算流场区域长度为3 m(保证了管内固液两相流充分发展)、直径为0.2 m的矿石输送管道二维模型,利用ICEM CFD 网格划分软件对模型进行四边形网格划分,考虑到仿真计算时间和精度,以压力损失梯度为指标对网格进行无关性验证,发现当网格单元数不低于12 652 时,仿真模拟得到的压力损失梯度相对变化小于2%,在可接受范围内,说明网格划分合适。
1.3 数学模型

图1 管道几何模型Fig.1 Pipe geometry model
扬矿管内的固液流态属于湍流流动,本文选取Euler-Euler 双流体模型模拟扬矿管内两相流的运动,该模型将固体颗粒视为连续性流体,颗粒和流体2 种介质在管内连续分布且可以相互渗透。不考虑相间热交换和质量交换,扬矿管内固液两相流动控制方程包括质量守恒方程、动量守恒方程以及湍流方程[13-15]。
1.3.1 液相控制方程
在直角坐标系下固-液两相湍流的液相连续性方程为
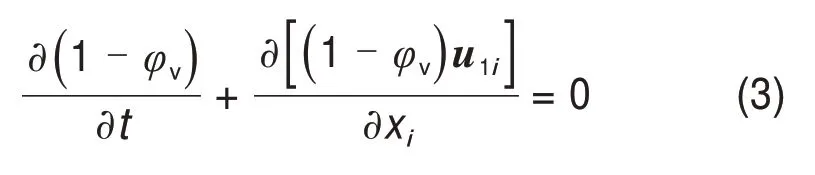
液相动量方程为

式中:φv为固相体积分数;u1为液相速度矢量;ρ1为液相密度;τ1为液相所受的应力张量;F1为液相单位质量的外力;M1为相间作用力;P为等效应力。
1.3.2 固相控制方程
固相连续方程为
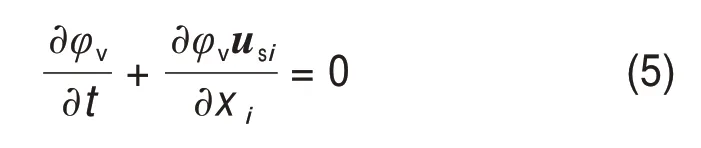
固相动量方程为
Key words: new engineering construction; basis of computer engineering; course system

式中:us为固相速度矢量;ρs为固相密度;τs为固相所受的应力张量;Fs为固相单位质量的外力;Ms为相间作用力。
流体流动选择常用的RNGk-ε湍流模型,该模型来源于严格的统计技术,相比于标准k-ε模型,RNGk-ε模型有更高的精度和可信度,适应性更强。关于湍动能k和湍动耗散率ε的输送方程见文献[16-17]。
颗粒水力提升过程中,其受到的力主要包括重力、浮力、轴向拖曳力、Basset力、Saffman力、Magnus力等[18-20]。其中Basset力仅在颗粒加速期间占主导作用,Saffman力在速度梯度较大场合比较重要,本文研究颗粒在扬矿管中稳定运动时的状态,且固体密度远远大于液体的密度,因此,本文只考虑曳力,曳力模型选择Gidaspow模型。
1.4 边界条件及求解方法
1)进口条件:进口边界设为速度入口,固相与液相速度相同且均匀分布,为3 m/s,方向沿管轴线方向;固相体积分数为10%,粒径为8 mm,固相密度为2 650 kg/m3,液相密度为1 045 kg/m3;设置湍流强度为3%,水力直径为200 mm。
2)出口条件:定义出口为自由出流边界。
3)壁面:采用无滑移壁面边界条件。
5)求解方法:基于有限体积法和SIMPLE算法对控制方程进行非稳态求解,时间步长设为0.001 s,每个时间步长最大迭代30次。
2 计算结果及分析
Fluent软件可以监测扬矿管选定面上某一项压力随时间的变化情况,对于固液两相流无法直接得到其总压,但分别可以得到该面上的静压及两相的动压,求和即可得到总压。用管道进口总压减去出口总压再除以管道长度,可得到该段管道内的压力损失梯度:

式中:∆p为压力损失梯度,Pa/m;pin管道为进口总压,Pa;pout为出口总压,Pa;h为管道长度。
总压的计算公式为
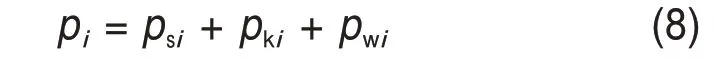
式中:pi为总压,Pa;psi为静压,Pa;pki为固相动压,Pa;pwi为液相动压,Pa。
本文选取仿真模型中y=0.3 m 至y=2.7 m 管段作为有效工作段进行压力损失梯度计算,并选择中间y=1.5 m处来研究颗粒体积分数和轴向速度沿径向的变化规律。因为仿真分析时发现该段范围内压力变化比较平稳,流体流动趋于稳定,没有出现和进口附近一样流场变化剧烈的情况。
2.1 摆幅对管道压力损失梯度的影响
图2所示为管道摆动周期为10 s,摆幅分别为1,2,3 和4 m 时,管道压力损失梯度随时间的变化情况。从图2可以看出:管道内压力损失梯度变化幅值随摆幅的增大而增大,但波动周期相同,总是等于管道摆动周期的一半,因为管道沿正负2个方向运动对管内流体的影响相同;摆幅分别为1,2,3 和4 m 的4 种工况下压力损失梯度最大值分别为1.425,1.429,1.424 和1.421 kPa/m,而根据初始条件进行稳态仿真计算得到研究管段压力损失梯度为1.424 kPa/m,几乎与摆动工况下压力损失梯度相等,最小值依次递减,分别为1.317,1.149,0.891和0.655 kPa/m。
波流联合作用使管道产生横向摆动,摆动加速度引起的附加惯性力使管内两相流产生径向运动,运动过程中颗粒与管壁、颗粒与颗粒之间的摩擦碰撞次数以及作用范围会增加,虽然此过程中会带来颗粒的部分能量损耗,但是波动能以管道摆动的形式从而带来两相流体势能项、动量项的增加明显占主导地位,因此,摆动工况下压力损失梯度比管道稳态工况时小,摆动幅度越大证明波动强度和能量也越大,管内流体能量增加也越大,压力损失梯度就越小。虽然管道在一定工况下的摆动会减小压力损失梯度,但是实际工作中应该综合考虑其他因素控制管道摆动幅度。

图2 不同摆幅下压力损失梯度随时间的变化规律Fig.2 Variation of pressure loss gradient with time at different swing amplitudes
2.2 摆幅对管道出口处颗粒平均体积分数的影响
图3所示为管道在管道摆动周期为10 s,摆幅分别为1,2,3和4 m的条件下,管道出口处颗粒平均体积分数随时间的变化曲线。从图3可知:摆幅分别为1,2,3 和4 m 的4 种工况下,管道出口处颗粒平均体积分数随时间呈周期性变化,且变化周期同样为摆动周期一半;周期一定,摆幅越大,平均体积分数变化幅度越大,在摆幅为4 m时瞬时最大值达到14%。这是由于摆幅越大时,管道摆动速度越大,产生的惯性力也越大,颗粒在惯性力的作用下向管壁聚集程度越严重,同时颗粒间由于聚集也会造成相互之间的挤压与摩擦,最终导致出口处颗粒平均体积分数随摆幅的增大而增大。系统在工作过程中,若管道壁面聚集体积分数过高会造成颗粒回流,堵管,管道磨损,甚至出现爆管的现象,因此,应该严格控制管道的摆动幅度。

图3 不同摆幅下管道出口平均颗粒体积分数随时间的变化规律Fig.3 Variation of average particle volume fraction of pipe outlet with time under different swing amplitudes
2.3 摆幅对颗粒体积分数径向分布的影响
鉴于上述分析可知:管道摆动对管道内两相流的影响在摆动正反2个方向是相同的,因此,只需分析管道在稳态以及摆幅分别为1,2,3 和4 m共5种工况下的半个周期内,颗粒体积体积分数在y=1.5 m处沿管径方向的分布规律,如图4所示。
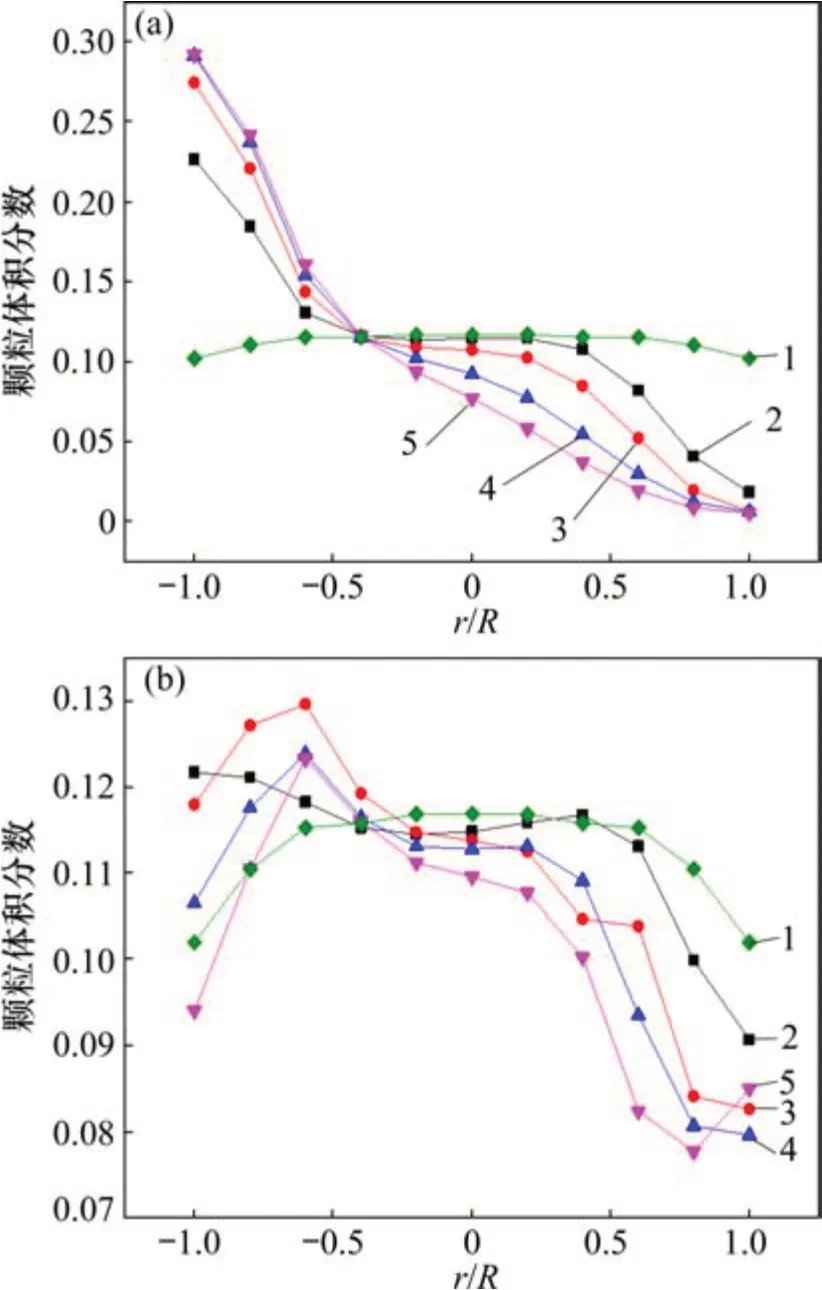
图4 不同摆幅下颗粒体积分数沿径向的分布Fig.4 Radial distribution of particle volume fraction atdifferent swing amplitudes
从图4可以看出:当管道向右摆动速度达到最大值时,即0.25T时刻,颗粒体积体积分数出现管道左侧体积分数高,右侧体积分数低的现象,左侧体积分数最高达到30%,且摆幅越大这种现象越明显,摆幅越小颗粒体积分数分布曲线越趋近稳态工况曲线;当管道向右摆动速度减为零时,即0.50T时刻,管道内径向颗粒体积体积分数最大值与最小值之差不超过5%。这是因为:横向摆动会使管道内固液两相流产生附加径向运动,从而改变两相流动局部参数。在摆动周期一定时,摆幅越大,管道摆动速度和加速度越大,附加惯性力也越大,颗粒在附加惯性力的作用下向左迁移聚集越多,导致管道左侧颗粒体积体积分数高,右侧体积分数低,出现明显的径向不均匀分布。当附加惯性力越小时,管道内两相流运动状态越平稳,颗粒体积体积分数分布越均匀,越不容易堵塞输送管道。因此,实际工作中应尽量减小输送系统摆幅,提高输送系统稳定性以及安全性。
2.4 摆幅对颗粒轴向速度分布的影响
图5所示为管道在摆幅分别为1,2,3 和4 m以及稳态共5 种工况下的0.50T内,颗粒轴向速度在y=1.5 m 处沿管径方向的分布情况。从图5可以看出:在0.25T时刻管道向右摆动速度达到最大值时,管道内颗粒轴向速度在管壁处为0 m/s,整体上呈现左侧速度高,右侧速度低的趋势,最高速度达到3.8 m/s,并且轴向速度基本以线性形式沿径向分布;摆动周期一定时,摆幅越大,颗粒轴向速度沿径向分布梯度越大,径向分布不对称性越严重;当管道向右摆动至速度为0 m/s 时,4 种摆动工况下,颗粒轴向速度沿径向的分布曲线基本与稳态时重合,最大速度差不超过0.5 m/s。这是因为:颗粒由于附加惯性力向运动相反方向聚集,颗粒与颗粒、颗粒与管壁的碰撞、摩擦次数以及作用范围增大,虽然相互作用过程会带来颗粒的能量消耗,但管道摆动使颗粒的动量项增加明显占主动地位,且离管壁越近,动量增加越大。摆幅越小,速度越小,附加惯性力也越小,颗粒轴向速度沿径向分布越均匀。

图5 不同摆幅下颗粒轴向速度沿径向的分布Fig.5 Radial distribution of axial velocity of particle at different swing amplitudes
3 实验验证
为验证仿真结果的准确性,在长沙矿冶研究院深海矿产资源开发利用国家重点实验室进行实验,实验所用的模拟颗粒采用密度与锰结核相近的结核代替,所有操作参数与仿真模拟工况相同,并通过施加背压的方法来模拟深海扬矿环境。由于实验条件限制,该平台只能模拟稳态工况下的扬矿作业。在离实验管道进口高度分别为0.3 m和2.7 m 处安装压力表,每隔2 min 记录一次各压力表读数,总共记录8 次,每次记录10 组数据并分别计算压力损失梯度,通过比较去除最大和最小的2组数据,对剩下8组数据求平均,并与仿真结果进行对比。实验与仿真结果如图6所示。整体而言,数值计算结果与实验结果基本吻合,二者相对误差在10%以内,说明实验结果能够较好地验证仿真结果的可信性。
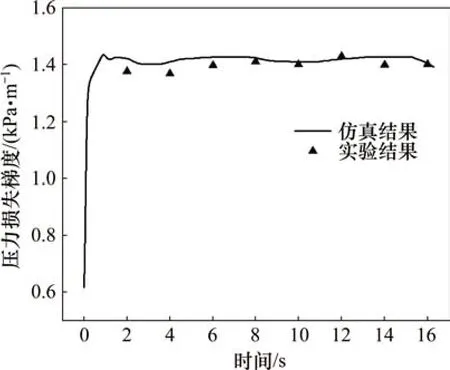
图6 压力损失梯度仿真结果与实验结果对比Fig.6 Comparison of pressure loss gradient simulation results with experimental results
4 结论
1)压力损失梯度和出口处颗粒平均体积分数随摆动呈周期性变化,周期为摆动周期一半;摆动周期一定时,摆幅越大,压力损失梯度和出口处颗粒平均体积分数变化幅值越剧烈;摆动工况下压力损失梯度比稳态工况下的小,而颗粒平均体积分数比稳态工况下的大,实际工作中应该综合考虑管道输送的安全性、稳定性和输送效率严格控制管道摆动幅度。
2)管道摆动周期一定时,摆幅越大,摆速越大,颗粒在管壁一侧聚集程度越高,颗粒浓度沿径向分布不均匀程度越严重,不利于矿物颗粒水力提升。
3)管道摆动对颗粒轴向速度沿径向分布影响较大,摆动工况下,颗粒轴向速度沿管径基本呈线性分布,摆幅越大,轴向速度沿径向分布梯度越大,径向不对称性越严重。
