基于模糊自适应Kalman滤波的MEMS惯导系统在线修正研究*
2019-11-14贠卫国
贠卫国,毕 凯,田 易,孟 真
0 引 言
MEMS惯性导航系统由于成本的限制,选用的传感器精度较低,导致惯性导航系统的解算误差会随着时间的增加而增大,因此惯性导航系统工作前须采用标定的方法来提高MEMS惯性导航系统的解算精度[1].确定性零偏、标度因数以及安装误差可以通过转台标定的方法来消除,但随机零偏每次上电启动都存在不确定性的问题,无法消除.因此,本文提出了一种基于自适应Kalman滤波估计随机零偏的方法来修正MEMS惯导系统.
MEMS惯导系统误差在线修正中通常采用基于Kalman的滤波方法[2,3]对陀螺和加速度计的误差进行在线估计,这种方法在外部环境影响较小的情况下效果是比较好的,但是在实际在线标定中,惯性导航系统很容易受到多种外部环境的干扰而导致观测噪声发生变化,进而影响滤波器性能,导致精度下降.因此Kalman滤波在噪声时变的情况下难以起到好的估计效果.针对噪声时变这一问题,不少学者对自适应滤波技术进行了研究,如 ‘渐消因子自适应Kalman滤波’可通过渐消因子对预测误差协方差进行调整来抑制滤波发散,但它在变量较多的情况下跟踪能力比较差[4].‘Sage-Husa滤波 ’的基本原理是基于历史观测数据的统计特性在线计算调节因子,计算量比较大,实时跟踪能力差[5].‘模糊自适应Kalman滤波’是一个实时调整噪声统计特性从而实时调整并估计的滤波模型,模型可以对时变的观测噪声进行准确估计,能够快速的逼近真实值,并且计算简单,得到了广泛的应用[6].
基于模糊自适应控制的Kalman滤波已经成功应用于导航系统,如Tseng Chien-Hao提出了一种基于组合卡尔曼滤波器(CKF)和模糊逻辑自适应系统(FLAS)的组合导航系统的传感器融合方法[7],成功的抑制了滤波发散.Li, Jing等在惯性导航初始对准中提出了无迹Kalman结合模糊自适应策略,提高了对准的稳定性[8].然而在线标定中,基于模糊控制的自适应Kalman却很少用到.因此作者提出了基于模糊自适应控制的Kalman滤波方法来实现陀螺和加速度计的随机误差的在线估计.
因此,本文针对观测噪声状态不准确时容易导致滤波发散的情况,该方法通过制定模糊规则,将观测变量残差的理论方差与实测方差迹的比值模糊化作为模糊推理的输入,姿态、速度和位置量测方差的修正因子作为输出,实时、精确的估计系统的观测噪声,提高了系统的稳定性以及修正效果.
1 误差模型
1.1 惯导系统误差模型
根据理想平台和导航计算的数学平台确定了以下的导航系统误差,系统的姿态误差和速度误差如下[9,10]:

(1)
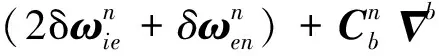
(2)
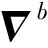
系统的位置误差公式如下:
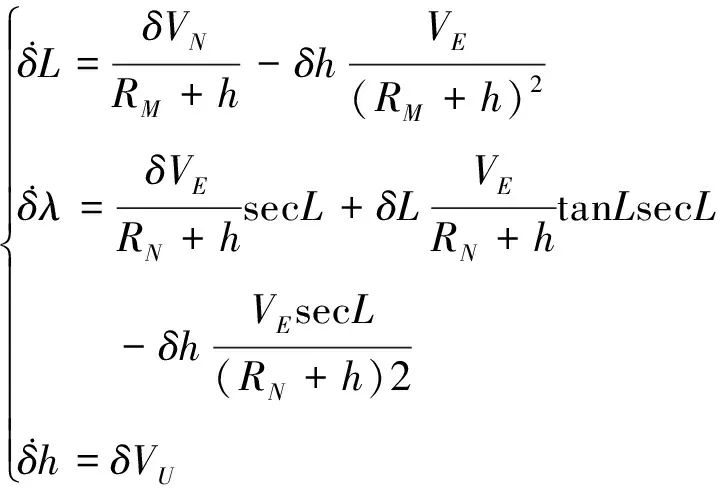
(3)
式中,δL表示纬度误差、δλ表示经度误差、δh表示高度误差、h表示高度、RM表示卯西圈半径、RN表示子午圈半径.
航向角误差和姿态误差角之间的关系式为:
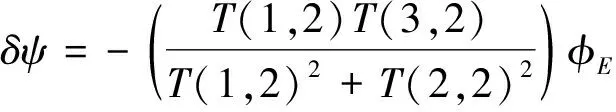

(4)

1.2 惯性器件误差模型
本文考虑到MEMS惯性器件的随机误差,得到陀螺仪和加速度计的误差模型[11]:

(5)
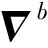
2 Kalman滤波算法
2.1 状态方程和观测方程
Kalman 滤波是一种线性最小方差估计[12],通过迭代运算,事先预测、校正更新估计的一组数学方程.在滤波算法中,首先是建立滤波的状态方程和观测方程.
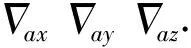
系统的状态方程为:
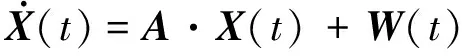
(6)
其中,A为状态矩阵,W为状态噪声,状态矩阵A为[13]:
其中,状态方程A中的每一个模块由误差模型以及对应的状态变量得出.
本文以惯性导航系统解算的航向角、速度、位置信息与参考航向角、GPS速度、位置的差值作为观测量,设VS、PS、ψS为惯性导航解算的速度、位置及航向角,VG、PG、ψG为参考的速度、位置及航向角,则观测变量为:
则系统观测方程为:
Z(t)=HX(t)+V(t)
(7)
其中,H为观测矩阵,V为观测噪声.系统观测矩阵为:
H=[H1H2]
其中:
H1=[H11H1201×10]
H11=-T(1,2)T(3,2)/(T(1,2)2+T(2,2)2
H12=-T(3,2)T(2,2)/(T(1,2)2+T(2,2)2)
2.2 Kalman滤波过程
将2.1节的状态方程和观测方程离散化,得到递推Kalman滤波器如下[14]:
状态一步预测:
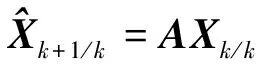
(8)
状态更新:
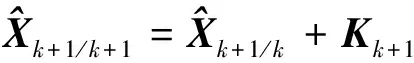
(9)
新息:
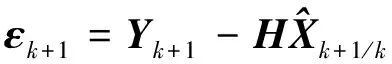
(10)
滤波增益矩阵:
Kk+1=Pk+1/kHT[HPk+1/kHT+R]-1
(11)
一步预测协方差:
Pk+1/k=APk/kΦT+ΓQΓT
(12)
协方差更新:
Pk+1/k+1=[In-Kk+1H]Pk+1/k
(13)
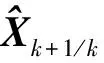
3 模糊控制
Kalman滤波器在对象模型足够准确时, 性能较好;但如果系统模型或噪声的统计特性不准确,过去的量测数据会直接影响现时状态估计的精度,严重时甚至导致滤波发散[15,16].因此,为了抑制Kalman滤波器发散,本文制定了模糊规则,通过输入残差的实测方差与理论方差迹的比值来对量测方差进行实时估计,并输出调整参数,对量测误差的参数进行估计和修正,以求获得更好的估计效果.
3.1 模糊逻辑
模糊理论不需要建立准确的数学模型,但能较好的反映事物的不确定性,它提供了一种有效的表示不确定性和不精确性的模糊算子和决策规则.本文主要对实测方差与理论方差迹的比值进行模糊化,得到论域上的模糊子集所对应的隶属度函数,当系统的观测噪声不平稳时,调整实测方差与理论方差迹的比值来使观测噪声的设定值逐渐逼近于真实噪声水平.
本文将观测信息分为两个模块,则残差的量测方差Ck和理论方差Sk如下:
式中,CψV和SψV分别为姿态和速度的实测方方差与理论方差,CP、SP分别为位置的实测方差与理论方差.
本文通过分别监测CψV、SψV和CP、SP来制定模糊规则,其中对应理论方差与实测方差迹的比值G1、G2作为模糊推理的输入,观测噪声的修正因子qψV,qP作为输出,当观测噪声的统计特性准确时,G1,G2的值应该1附近,当系统的测量噪声的实际值与给定值不一致时,G1,G2将偏离1,即当G1、G2大于1时,则系统的理论方差大于实测方差,应该增大修正因子qψV、qP,使G1、G2接近于1,同理,当系统理论方差小于实测方差时,应当减小qψV、qP.

系统中G1、G2采用相同的输入G,qψV、qP采用相同的输出q,建立模糊推理规则为:
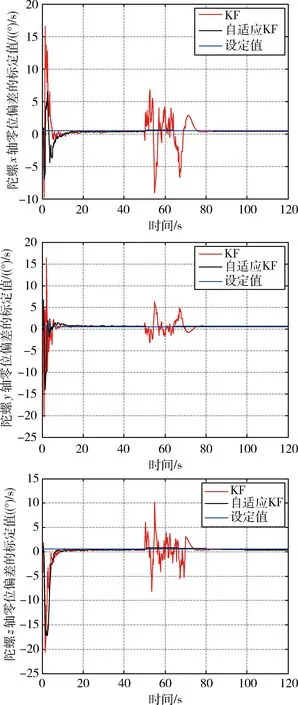
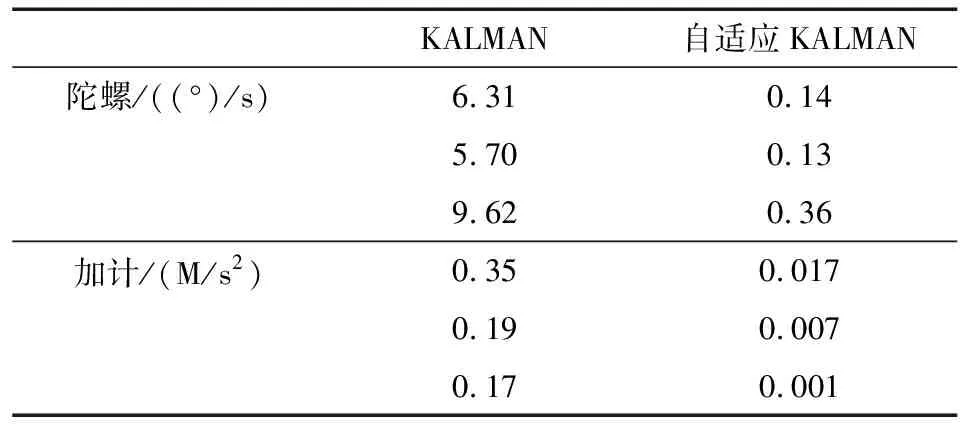
if 1.5 if 0.5 if 0 得到输出的修正因子为: if ′∈MA′,q=1+0.5·N if ′∈M′,q=1+0.3,(1-N)·sign(G-1) if ′∈MI′,q=1-0.5·N 其中N为输入隶属度函数得到的隶属模糊度. 模糊自适应Kalman滤波器是根据3.1节所得的修正因子来实时修正常规Kalman滤波过程中的观测噪声,式(14)中,qψV修正姿态和速度的观测噪声,qP修正位置的观测噪声,修正过程如下式: (14) 上式中qψV和qP是由上一步滤波过程中的实测方差和理论方差决定. 实测方差和理论方差的求取过程如下.式(10)中,新息ε被称为残差向量,它反映了滤波模型的准确性.残差的量测方差为: Ck=εk·εkT (15) 由于本文的观测噪声是由简单的统计特性得到的,但观测噪声经常受到外部环境的影响,容易导致滤波发散,因此需要对式(15)进行数据平滑操作,得到平滑新息测量方差为: Ck=Ck-1·(1-dk)+dkεkεkT (16) dk=(1-b)/(1-bk+1) (17) 式(19)中,d为遗忘因子,b为遗忘因子中的参数,通常b的取值为[0.95,0.995]. 定义残差的理论方差为 Sk=Hk(AkPkAkT+Qk)HkT+Rk (18) 那么,残差的理论方差与实测方差的迹的比值为: (19) 其中,tr表示矩阵的迹. 图1为模糊自适应Kalman滤波的算法流程图. 图1 模糊自适应Kalman滤波算法流程图Fig.1 Flow chart of fuzzy adaptive Kalman filtering algorithm 为了实现对惯性导航系统中惯性器件误差的有效在线估计和补偿,本文需研究载体不同机动方式对惯性传感器误差带来的影响与激励效果. 本文利用奇异值分解理论的方法进行可观测分析,由于在奇异值分解的过程中有引入外测设备的信息,一般利用离散型系统的模型对系统进行奇异值分解.首先需要线性时变系统进行分段处理,则将表达式写成离散型分段式定常系统形式[18]PWCS(Piece-Wise Constant System). 离散化后的状态方程和观测方程如下 (20) 式中:Xk∈Rn;Zk∈Rm;Fj∈Rn×n;Hj∈Rm×n;Fj和Hj均为常值矩阵.则线性系统的可观测性矩阵可表示为: 其中, 式中,Qj为线性时变系统中第i时间段nmxn阶的可观测性矩阵.同时,时变系统的可观测性矩阵(SOM,Stripped Observability Matrix)为: Qs(r)=[Q1Q2…Qr]T (21) 奇异值的分解如下: 存在矩阵A∈Rm×n,那么存在正交矩阵U1∈Rm×m和U2∈Rn×n,使得A=U1∑U2T,式中 且对角元素等于S=diag{σ1,…,σr}为对角阵,σ1≥σ2≥…≥σr≥0顺序排列. 本文在用奇异值分解方法分析时变系统可观测性与状态可观测度时,通过奇异值的分解,各状态量对应的奇异值的相对大小就反映了各状态量的相对可观测性. 通过对四种简单路径的可观测分析,可以得到与状态方程中相对应的15个状态变量的奇异值如表1. 表1 不同状态下的奇异值Tab.1 Singular values in different states 表1表示的是15种状态变量在不同路径下的奇异值,通过奇异值的大小可以判断系统的可观测性.为了能更简便的区分可观测度的大小,准确的估计出误差参数,本文设奇异值小于1的不可观测,因此, 由上表可得: 在匀速直线运动状态下,陀螺的z轴零偏和加计的零偏的奇异值太小,则不可观测;在加速直线运动下,加计的x,y轴零偏可观测度较低;在转弯运动中,加计零偏的可观测性相对来说较低;圆周运动中,陀螺和加计零偏的可观测性相对来说都比较好. 通过以上可观测分析,路径的设计如下图2,设载体所在的初始纬度为45°,初始经度为118°,仿真路径开始为指北方向,路径行驶分为以下三种不同的阶段: ①指北方位匀速直线运动,该轨迹中陀螺的x轴零偏和y轴零偏的可观测性比较好. ②拐弯至东北方位加速直线运动,x轴加计零偏和z轴加计零偏的可观测性比较好. ③圆周运动,可标定出陀螺z轴零偏和y轴加计的零偏. 图2 载体仿真轨迹Fig.2 Carrier simulation track 通过可观测分析可知,在以上设计的路径中,陀螺和加计的误差参数模型的可观测性比较好.在这三种路径轨迹的行驶下,可以标定出陀螺和加速度计三轴的随机零偏. 本次在线估计的仿真时间是120 s, 初始平台误差角为0.5(°)/s,初始速度误差为0.1 m/s,初始位置误差为1.5 m.惯导系统的状态噪声均方差为: Q=[(0.3(°)/s)2(0.3(°)/s)2(0.3(°)/s)2(0.2m/s2)2(0.2m/s2)2(0.2m/s2)20 0 0 0 0 0 0 0 0]. 观测噪声均方差为: R=[(0.5(°)/s)2(0.2 m/s)2(0.2 m/s)2(0.2 m/s)2(2 m)2(2 m)2(2 m)2]. 仿真阶段在50 s至70 s给观测量加入干扰噪声,航向角加入的干扰噪声为1(°)/s的随机噪声,速度加入干扰噪声为5 m/s的随机噪声,位置加入干扰噪声为7 m的随机噪声.设置陀螺的随机零偏为0.5(°)/s,设置加速度计的随机零偏为0.8 m/s2.如下图为在线估计随机零偏的仿真结果: 图3 陀螺随机零偏的两种不同滤波估计结果Fig.3 Two different filtering estimation results of gyro random zero offset 图4 加计随机零偏的两种不同滤波估计结果Fig.4 Adds two different filtering estimates for random zero bias 表2为系统的观测噪声发生变化时Kalman滤波与自适应Kalman滤波的估计结果与设定的标准值之间的最大误差对比. 表2 观测噪声变化两种不同滤波下陀螺和加计随机零偏估计结果误差Tab.2 Observed noise variation gyro and additive random zero-offset estimation error under two different filtering 由图3和图4的结果可知,Kalman滤波和自适应Kalman滤波都能很快收敛到设定值,但是在观测噪声受到外部环境影响而变化比较大时,从仿真结果和表2来看Kalman滤波标定的结果在受到影响时跳变比较大,而自适应Kalman滤波比常规Kalman滤波更收敛,几乎没有变化,将误差减小了二十几倍,可以更稳定的估计出陀螺和加速度计的随机零偏,因此,该方案具备更强的抗干扰能力,可以更有效的估计MEMS惯导系统的随机零偏来提高导航精度. 由于在MEMS惯性导航系统中传感器零偏存在随机启动的不确定性误差,以及Kalman滤波估计中观测噪声的统计特性不准确,容易受外部环境影响导致滤波发散,因此本文提出了一种自适应Kalman滤波在线估计随机零偏的方法来提高MEMS惯导系统的精度.本文首先介绍了惯性导航系统的误差模型和模糊自适应Kalman滤波算法,然后建立状态方程以及观测方程,并进行载体仿真路径的设计及分析,然后通过在线仿真得出了两种不同滤波的标定结果,由图3、图4以及表2可以得出,在观测噪声受到外部环境影响而发散时,自适应Kalman滤波在估计的过程中抑制了这种发散,相比常规Kalman滤波来说,更稳定的估计出了系统的随机零偏,因此,本文提出的方法具有更好的实用性.3.2 模糊自适应Kalman滤波
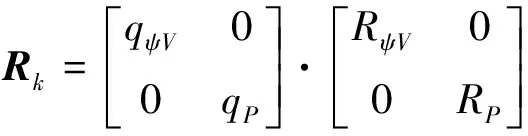

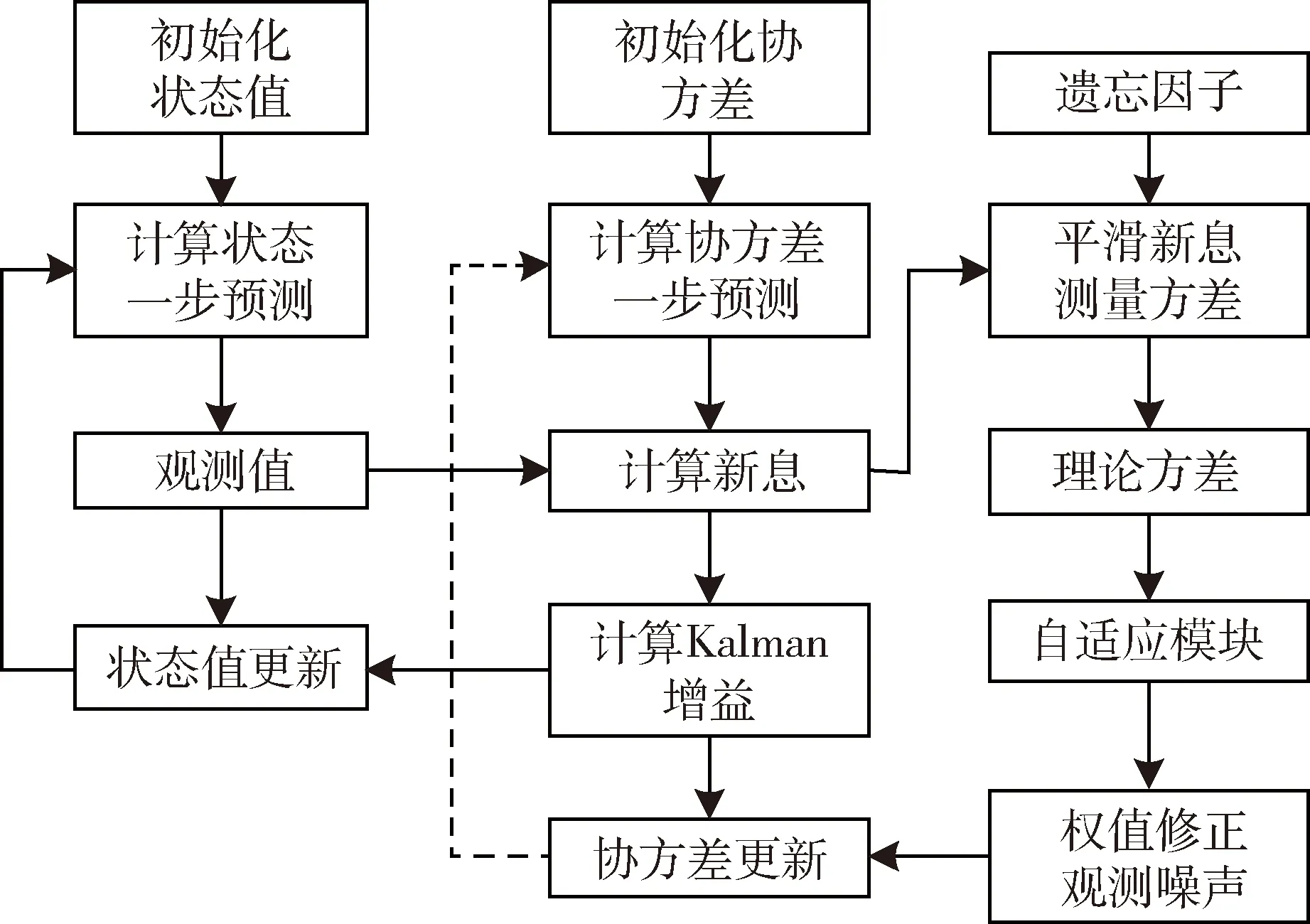
4 载体路径的分析及设计
4.1 可观测性分析

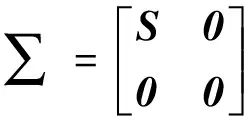
4.2 可观测性分析仿真

4.3 路径设计
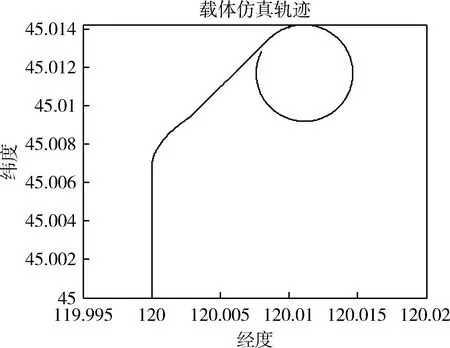
5 仿真及结果分析

6 结 论
