光伏并网逆变器的分段光滑模型
2019-11-13廖志贤罗丹黄国现蒋品群
廖志贤 罗丹 黄国现 蒋品群

摘 要:首先,由单相全桥光伏并网逆变器的等效电路出发,分析其工作原理,通过双极性SPWM控制的开关状态,建立了单相光伏并网逆变器的分段光滑模型。然后分析线性预测控制方法在该模型下的实现,利用四阶龙格-库塔法求解分段光滑模型的方程。最后,将数值模拟结果导入Simulink进行分析,对逆变器的输出电压、电流的时域波形和频域波形进行分析,结果表明:所建立的单相光伏并网逆变器模型是有效的,在耦合电感为3mH、开关周期20μs条件下,逆变器输出电流总谐波失真度分别为2.24%,满足并网标准。该模型对光伏并网逆变器的建模分析及工程设计,具有一定的参考价值。
关键词:光伏 分段光滑 并网逆变器 电流跟踪
中图分类号:0545 文献标识码:A 文章编号:1674-098X(2019)06(b)-0074-03
电网越来越走向对等化、智能化、网络化方向发展[1]。未来,光伏并网逆变器是电网的重要组成部分[2],其性能与电网的稳定运行息息相关,为此,光伏并网逆变器的建模分析方法得到了广泛关注。
在当前能源互联网不断推进的大背景下,如何找到更合适的分析建模方法[3],是一个关键问题。对光伏并网逆变器建模,主要分为小信号模型法和开关模型法,由于小信号模型进行了线性化处理,忽略了系统的开关非线性特性,因此是不精确的,而开关模型法则非常适合光伏并网逆变器这种强非线性系统。基于此,本文在分析单相光伏并网逆变器的工作原理后,建立其分段光滑模型,并利用四阶龙格-库塔法解方程,利用线性预测控制方法进行控制,对未来大规模并网逆变器的组网数值模拟分析,具有一定的参考价值。
1 模型与方法
1.1 单相光伏并网逆变器电路分析
光伏并网逆变器并网运行等效电路如图1所示。upv为光伏阵列的输出电压,uinv为光伏并网逆变器全桥电路输出电压,ug为低压公共电网(220Vac,50Hz)电压,RL为光伏并网逆变器输出线路等效电阻,L为逆变器输出滤波电感,io为光伏并网逆变器输出电流。
光伏并网逆变器工作时,uinv是受控电压,ug是电网电压,可认为电网电压是给定值,控制器通过调节SPWM信号控制uinv的大小,可控制电感两端电压值,间接控制电感电流,即逆变器的输出电流io。
1.2 光伏并网逆变器的分段光滑模型
由圖1光伏并网逆变器并网运行等效电路可知,输出电流io大小主要由电感两端电压uL决定。由于电网电压ug是给定的信号,通过控制全桥电路输出电压,可控制输出电感两端电压uL,进而控制输出电流io大小。根据KVL原理,单相光伏并网逆变器电压回路微分方程如下。
(1)
令Mx=1表示开关管Mx导通,Mx=0表示开关管Mx关断,其中,x=(1,2,3,4)。根据双极性SPWM控制原理可知,全桥四开关的开关状态有两种:
状态1—M1=M4=1;M2=M3=0;
状态2—M1=M4=0;M2=M3=1。
设置开关状态符号S,其表达式如下:
(2)
则uinv表达式如下:
(3)
(1)式变为:
(4)
单相光伏并网逆变器的输出方程为:
(5)
2 控制实现
采用线性预测控制方法[4],可得控制项uinv的离散表达式:
(6)
(6)式中,TS为开关周期,kTS时刻输出电压、输出电流分别为uinv(k)、io(k),令,可使时间点(k+1)TS输出的电流io(k+1)跟踪参考电流iref(k+1),实现光伏并网逆变器的输出电流控制。
利用(6)式,计算出控制项uinv的值后,与三角波信号utri进行比较,可得开关S信号,如图2所示。
3 数值模拟结果
利用四阶龙格库塔法进行数值求解微分方程,根据(4)式方程和(6)式的控制项迭代表达式,进行数值模拟,参数取值如表1所示。
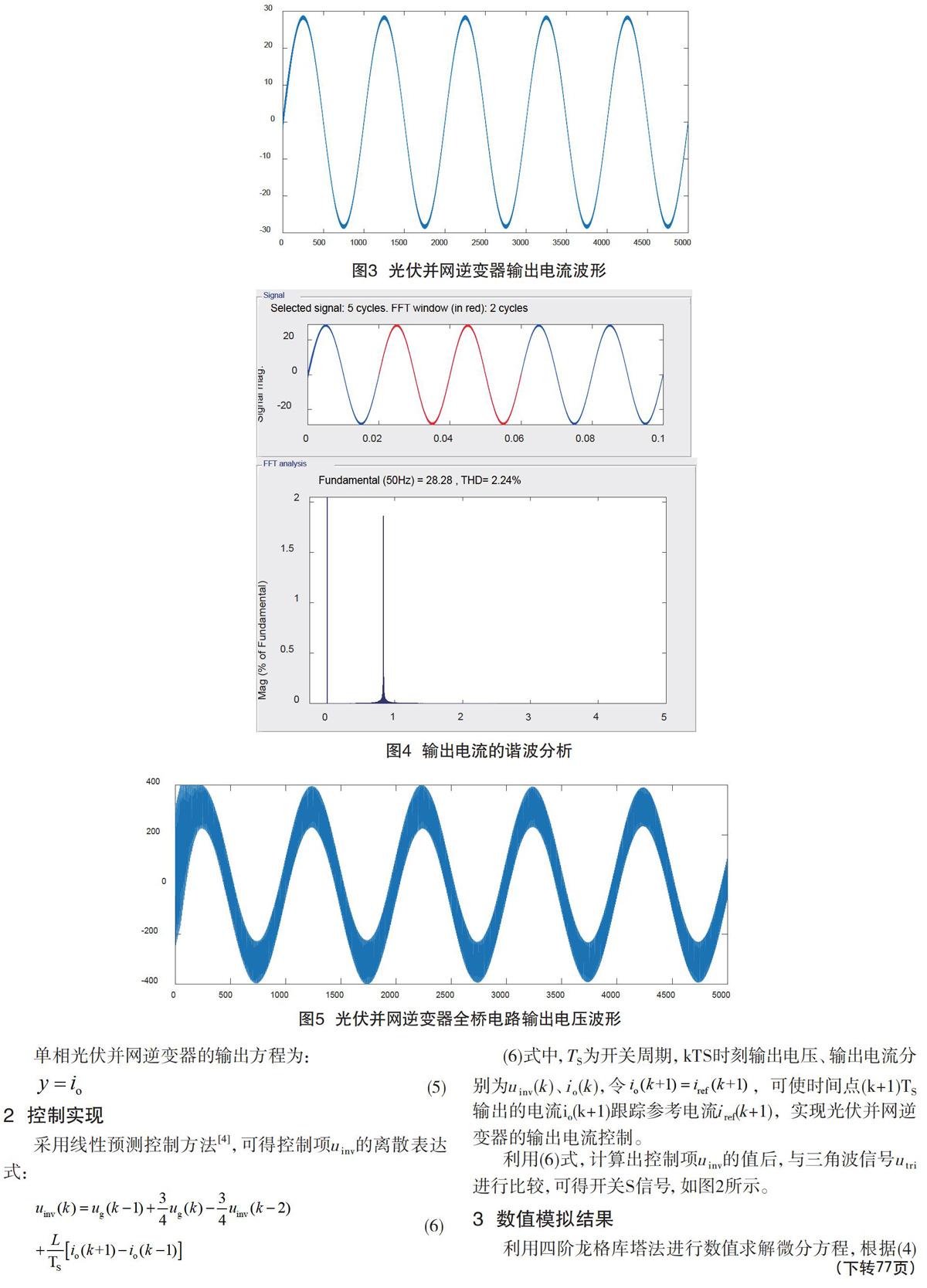
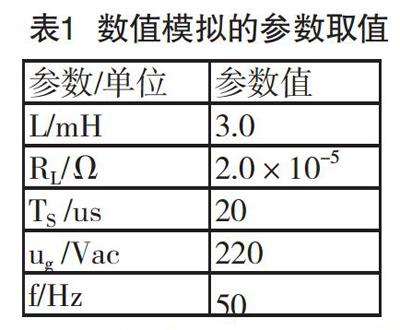
数值模拟结果如图3-图5所示,图3为光伏并网逆变器的输出电流波形,图4为输出电流的谐波分析图,图5为光伏并网逆变器全桥电路输出电压波形。
由图4可知,输出电流总谐波失真度(THD)为2.24%,满足并网标准,即≤5%。
4 结语
建立的光伏并网逆变器的分段光滑模型,利用线性预测控制方法进行控制,经数值模拟、分析,证明该模型的准确性。在此基础上,其他研究人员可选取不同的控制方法和参数,进行多机并联系统建模分析,本研究结果对光伏并网系统的研究和设计提供较好的参考。
参考文献
[1] Bedi G, Venayagamoorthy GK, Singh R, et al. Review of Internet of Things (IoT) in Electric Power and Energy Systems[J]. IEEE Internet of Things Journal, 2018, 5 (2): 847-870.
[2] Wang D, Liu L, Jia H, et al. Review of key problems related to integrated energy distribution systems[J]. CSEE Journal of Power and Energy Systems, 2018, 4 (2): 130-145.
[3] Lindner M, Witzmann R. Modelling and validation of an inverter featuring local voltage control Q(V) for transient stability and interaction analyses[J]. International Journal of Electrical Power & Energy Systems, 2018(101):280-288.
[4] 廖志贤,罗晓曙,何婷婷.一种光伏并网逆变器的数字化同步控制方法[J].计算机测量与控制,2012,20(8):2121-2123.
