电路原理课程中的对偶
2019-11-13黎小慧
黎小慧


【摘 要】鉴于非电子院校的电路原理课程教与学的困难,笔者从电路元件、网络定理与电路分析方法三方面提出对偶原理的基本性质,给教学提供一种基本思路。
【关键词】对偶原理;电路元件;网络定理
中图分类号: TM13-4 文献标识码: A 文章编号: 2095-2457(2019)30-0049-002
DOI:10.19694/j.cnki.issn2095-2457.2019.30.023
0 引言
针对医学院校影像专业学生,在既没有电子学习大环境,也无电路基础前提下,学习电路原理这门专业基础课程通常比较吃力,尤其对复杂电路的分析方法。因此,有必要从电路原理的教学方法上进行创新。通过多年的教学摸索,发现这门课程中有很多相似性知识点,即对偶性质[1]。如若能将它们之间的关联融汇到课堂,那将有效提高无论是教学还是学习该课程的效率。以下从电路元件、网络定理及其分析方法上详细理出它们的对偶性质。
1 电路元件的对偶
1.1 激励源
电路原理中,给电路提供工作信号的输入模型称为激励源,也叫独立源。属于理想的二端元器件,分为独立电压源和独立电流源。下面从两个元件的特点以及其在叠加定理中置零处理来分析其对偶特性。
独立电压源:为外电路提供电压,其电压值大小仅仅只与本身性质有关,源一旦给定,则电压值就恒定或是固定的某个函数关系。但是端电流则跟电压源提供的电压值与外电路严密的结合,就算源不变,如果外电路改变时,端电流也会随之变化。在叠加定理中,当一个独立源单独作用时,其余别的独立源置零,如果是电压源置零的含义为短接[2]。
独立电流源:为外电路提供电流,其电流值大小仅仅只与本身性质有关,而与外电路的结构无任何关系,源一旦给定,则电流值就恒定或是固定的某个函数关系。但是端电压则跟电流源提供的电流值与外电路严密的结合,就算源不变,如果外电路变化的时候,端电压也可能随之变化[2]。
从以上可以看出,两个独立源在向外提供电压电流和端电压电流的特性上完全对偶。并且在叠加定理中置零为短路和开路处理,这也是对偶性质的体现。
1.2 受控源
在电路中,存在一种元件,本身不是源,但是它的存在,使该条支路的电压或电流牵制于电路中另外一条支路的电压或电流。根据其控制支路的受控量是电压还是电流,可以分为两大类:受控电压源和受控电流源。又根据其控制变量再可以细分为电流控制或电压控制,由此衍生出四种受控源:电压控电流源(VCCS)、电压控电压源(VCVS)、电流控制电流源(CVCS)、电流控制电压源(CVVS)。
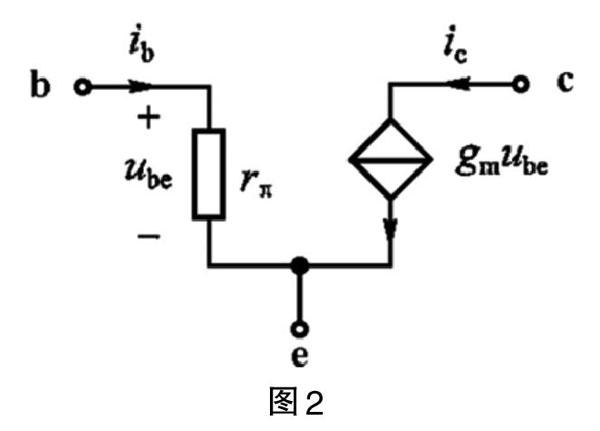
比如,一个晶体三极管的元件如图1,它的电路基本原理是给控制集极的电流值ic,大小由基极的电压ube所控制,即ic=gmube,其中gm为一常量,称之为转移电导。电路模型如图2所示,就相当于一个电压控制电流源(VCCS)。
图1 图2
同理,根据元件在电路中产生的参数及耦合因数,提出另外三种受控源对比如表1:
表1 四种受控源基本量的对比分析表
这四种源的分析形式不论从其控制变量还是从受控变量来说,包括变量前面的系数都具备对偶性,我们只需要就其中一种源来讨论分析,其他的性质对照关联变量即能掌握。如此对含有受控源的电路分析难度大大减小。
1.3 线性动态元件
在线性动态元件中提出两个元件,电容元件与电感元件。这两个元件在电路中都具备贮存能量的特点,根据贮存能量类型不相同,对应了元件VCR(电压电流关系)的对偶关系。如电容元件是贮存电场能量的元件,贮存电荷量与端电压成正比关系,正比系数就是电容元件的电容值大小。对于电容元件的端电流是因为电容极板电荷变化而产生,大小等于电容电荷的变化率,由此推出电容元件的VCR关系为i(t)=C■。而电感元件是贮存磁场能量的元件,产生的磁链与端电流成正比关系,正比系数就是电感元件的电感值大小。对于电感元件的端电压是因为线圈中磁链发生变化而产生的感应电动势,其大小等于电感磁链随时间的变化率,由此推出电感元件的VCR关系为u(t)=L■。
從两个元件的本身的特性参数来说,L值和C值就是一个对偶的参数,然后再看其端电压电流关系,虽然其微观机理不尽相同,但是元件VCR的确呈现明显的对偶关系。同样,在学习这两个元件性质的时候,只需重点掌握其中一个,另一个直接用对偶式导出。
2 网络定理的对偶
电路原理的分析实质是对网络的分析,一般情况,如果只需要分析网络的某条支路参量时,可以选取将支路以外的部分网络进行等效,也就产生了戴维南等效和诺顿等效电路。
戴维南等效:将一个网络对某个端口产生的效应可以等效成为一个独立的电压源和一个电阻的串联模式。其中,独立电压源的电压值大小为这个网络在端口开路的时候的端口开路电压,串联电阻值的大小为网络内所有的独立源置零的时候从端口看进去的等效电阻[3]。
诺顿等效:将一个网络对某个端口产生的效应可以等效成为一个独立的电流源和一个电阻的并联模式。其中,独立电流源的电流值大小为这个网络在端口短路的时候的端口短路电流,并联电阻值的大小为网络内所有的独立源置零的时候从端口看进去的等效电阻[4]。
由定理内容不难发现,戴中是等效为电压源和电阻的串联,诺为电流源与电阻的并联,两等效的电阻值不变,这也是对偶的一种表现。并且,因为同为一个网络的等效图,戴和诺又能相互等效,于是有:uoc(t)=isc(t)Req
