水泥基材料接触溶蚀的三维有限元数值模拟

2019-11-13

长江科学院院报 2019年11期

(武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

1 研究背景

钙溶出性侵蚀是水泥基材料耐久性病害的一类，又称溶蚀[1]，根据水泥基材料所处的环境的不同，可分为接触溶蚀与渗透溶蚀[2]。接触溶蚀是指水泥基材料在与水接触过程中，水头较低，水泥基材料内部未形成渗流作用或渗流作用效应可以忽略时，孔隙液中的钙离子在浓度梯度作用下，不断向外扩散，打破了固液两相钙浓度间的平衡关系，使得固相钙不断溶出的过程[3]。

在自然条件下，接触溶蚀过程十分缓慢，溶蚀锋面由表及里移动缓慢[4-5]。据报道，建筑物与水接触100 a，溶蚀锋面仅向前移动5～10 mm[6]，这一溶蚀特性对水泥基材料钙溶蚀性能的研究增加了一定的难度。为了能在短时间内研究溶蚀对水泥基材料各方面性能的影响，加速溶蚀试验和溶蚀数值模拟成了众多学者研究溶蚀的2种方法。在数值模拟方面，国内外学者做了大量的研究。Reardon等[7]研究了水泥水化物与孔隙液中离子间的热动力平衡关系；Berner[8]建立了孔隙液中钙离子浓度与水基材料中钙含量之间的固液平衡关系；Gérard等[9]修正了固液平衡关系，建立起简化的一维钙溶蚀数学模型；Nguyen等[10]结合尺度均质化分析建立了混凝土钙离子浸出模型，引入孔隙曲折率来考虑骨料对溶蚀的影响；Wan等[11]通过试验得到了波特兰水泥基材料在6 mol/L的硝酸铵溶液中的固液平衡关系曲线，并据此建立了加速水泥净浆溶蚀的一维数学模型[6]； Yu等[12]耦合化学动力学与化学热力学提出了针对采用6 mol/L的硝酸铵溶液加速接触溶蚀的一类新的模拟方法。

纵观以上研究发现，水泥基材料接触溶蚀数值模拟方法虽然较多，但大多以一维展开，求解方法以有限差分法为主，对于采用三维有限元方法模拟接触溶蚀尚未见报道。对此，本文针对水泥基材料接触溶蚀的三维有限元数值模拟展开研究，拟通过建立三维接触溶蚀数学模型，采用FORTRAN语言设计有限元计算程序，通过数值计算研究各溶蚀特征量的时空分布规律。

2 三维钙溶蚀数学模型

相关研究表明，水泥基材料在溶蚀过程中，钙、硫、钾、铝等元素为主要溶出元素，而氢氧化钙、水化硅酸钙凝胶又是水泥的主要水化产物，因此，以钙元素作为研究对象，可以较好地反映水泥基材料性能退化情况[13]。

参考现有的研究成果，本文根据钙离子传输数学模型、固液平衡关系、孔隙率演化模型、有效扩散系数模型建立三维钙溶蚀数学模型，并作如下假设：①孔隙液中的钙离子与固相钙含量之间瞬间达到平衡状态，即忽略固体钙溶解的时间效应;②不考虑孔隙液中钙离子与固体骨架产生吸附与解吸作用;③不考虑温度对溶蚀的影响;④材料各向同性。

图1 表征体元内的质量守恒Fig.1 Conservation of mass in representative elementary volume

2.1 钙离子传输数学模型

2.1.1 钙离子传输控制方程

在求解域内任取一

个长、宽、高分别为Δx，Δy，Δz的六面体表征体元(REV)，如图1所示。在域内仅考虑钙离子扩散作用，根据表征体元内钙离子的质量守恒关系，结合非克(Fick)第二定律可推导出水泥基材料溶蚀过程中钙离子传输控制方程。

如图1所示的表征体元，单位时间内x方向进入的钙离子通量为

(1)

式中：Jx为x方向进入的钙离子通量；Ax为表征体元侧面面积；φ为孔隙率；Dx为x方向扩散系数；C为孔隙液中钙离子浓度。

单位时间内x方向从表征体元流出的钙离子通量为

(Jx+ΔJx)Ax=

(2)

根据式(1)和式(2)可得，单位时间内在x方向从表征体元进入和流出的钙离子通量的差值即为净有流入量，如式(3)所示。

同理可得，单位时间内在y方向、z方向的净有流入量，分别如式(4)和式(5)所示。

式中：Jy为y方向进入的钙离子通量；Ay为表征体元侧面面积；Dy为y方向扩散系数；Jz为z方向进入的钙离子通量；Az为表征体元侧面面积；Dz为z方向扩散系数。

在溶蚀过程中，固相钙不断向孔隙液中溶解，假设固相钙的摩尔浓度为CS，单位时间内表征体元孔隙液内增加的钙离子物质的量ΔQ1为

(6)

式中t为溶蚀时间。

水泥基材料为多孔介质，假设孔隙内充满孔隙液，则表征体元中孔隙液的体积为φΔxΔyΔz，由此可得表征体元内孔隙液中钙离子含量为φΔxΔyΔzC，单位时间内表征体元中钙离子的物质变化量ΔQ2为

(7)

根据质量守恒定律，单位时间内x，y，z方向的钙离子净有流入量与孔隙液中因固相钙溶解的钙离子增加量之和等于单位时间内表征体元中钙离子的物质变化量，即

(8)

需要指出的是式中Dx，Dy，Dz为钙离子在孔隙液中不同方向的扩散系数，经体积均匀化后得到有效扩散系数，即

(9)

将式(9)代入式(8)整理可得钙离子三维传输控制方程，即

(10)

2.1.2 定解条件

求解上述控制方程组，给定初始条件与边界条件如下所述。

(1)初始条件：

C(x,y,z,t0)=C0。

(11)

式中C0为初始时刻孔隙液中钙离子浓度。

(2)边界条件：

①定通量边界条件为

(12)

式中：q为边界上已知钙离子的扩散通量；nx，ny，nz为边界的单位外法线方向余弦分量。

②离子交换边界条件[4, 14]。在以往的研究中，钙溶蚀数学模型边界条件多采用第一类边界条件，即0浓度边界条件，这一类边界条件在模型求解过程中，边界各点孔隙液浓度始终保持为0。由固液平衡关系可知，边界各点的固相钙浓度也始终保持为0，即边界各点瞬间完成钙溶出过程，这显然与事实不符；实质上，随着靠近边界侧的求解域内的浓度梯度变化，边界各点的孔隙液浓度也在不断发生变化。因此，采用物质交换边界条件更为符合实际情况，这类边界条件认为经过边界的钙离子通量与边界孔隙中钙离子浓度C与环境水中钙离子浓度C1之差成正比，其表达式如式(13)所示。采用这类边界条件不仅可以反映边界浓度变化，还可以通过边界浓度求解钙离子累积溶出量。本文采用该类边界条件作为接触边界条件,即

式中：kT为边界上孔隙液与环境水之间的传质系数；C1为环境水中钙离子浓度。

2.2 固液平衡关系

控制方程式的固相钙浓度CS与液相钙浓度C并非独立变量，相关研究表明，CS与C两者具有一定的热动力平衡关系[7-8]。Buil’s等提出了一种便于计算的等温平衡关系模型，Nakarai等进一步修正了Buil’s模型得到固液平衡曲线[4]，Berner通过试验数据验证了该模型的合理性[8]。本文引用该固液平衡曲线得到C与CS间的关系，即

式中：x1为C-S-H(水化硅酸钙凝胶)开始快速溶解时孔隙液中的钙离子浓度；x2为Ca(OH)2完全溶解时孔隙液中的钙离子浓度；Csatu为孔隙液中钙离子饱和浓度；CCSH为水泥基材料中C-S-H的摩尔浓度；CCH为水泥基材料中Ca(OH)2的摩尔浓度。

根据固液平衡关系，钙离子传输控制方程中固相钙浓度可转化为孔隙液中钙离子浓度，进一步得到含单一变量的控制方程，即

(15)

2.3 孔隙率演化模型

2.3.1 初始孔隙率计算

水泥基材料内部孔隙分为毛细孔与凝胶孔，即

φp0=φc0+φg0。

(16)

式中：φp0为水泥浆体的初始孔隙率；φc0为水泥浆体初始毛细孔隙率；φg0为水泥浆体初始凝胶孔隙率。φc0与φg0根据POWERS模型计算可得，即

(17)

式中：W/C为水灰比；α为水化度，可由式(18)计算。

(18)

根据水泥浆体在水泥基材料的体积占比，可计算水泥基材料的初始孔隙率，即

φ0=fp/mfm/cφp0。

(19)

式中：φ0为水泥基材料初始孔隙率;fp/m为水泥浆在砂浆中的体积分数；fm/c为砂浆在混凝土中的体积分数。

2.3.2 孔隙率演化

随着溶蚀过程的进行，Ca(OH)2与C-S-H等水化产物不断向孔隙液中溶解，使得孔隙体积不断增大，因而材料孔隙率也不断增大。考虑到C-S-H溶解过程较为复杂，假设C-S-H以Ca(OH)2形式溶解[4, 6]，据此可建立孔隙率演化模型，即

(20)

式中：Δφ为孔隙率变化量；ΔCS为固相钙浓度变化量；MCH为Ca(OH)2的摩尔质量；ρCH为Ca(OH)2的密度；CS0为初始固相钙浓度。

假设Ca(OH)2的溶解主要造成毛细孔的增加，而C-S-H的溶解在引起凝胶孔增大的同时，也会造成毛细孔的增大[5]。引入分配系数γ来考虑C-S-H的溶解对毛细孔隙率的影响，因此，可用式(21)、式(22)分别描述毛细孔隙率与凝胶孔隙率的变化。

(21)

(22)

2.4 扩散系数演化模型

目前，有效扩散系数模型均建立在不含粗骨料的水泥净浆或砂浆的基础上，对于含有粗骨料的水泥基材料无法适用。相关研究表明[15]，粗骨料对于扩散系数的影响主要有2方面：一方面，粗骨料所在区域无扩散现象发生；另一方面，粗骨料与水泥浆间存在界面过渡区，会造成孔隙增大，进而加剧扩散。为此，相关研究引入孔隙曲折度来考虑粗骨料对扩散系数的综合影响，建立水泥基材料的通用扩散系数模型，如式(23)所示。

(23)

3 有限元计算方法

3.1 计算格式

采用三维8节点等参单元离散空间域，试探函数为式(24)所示。

(24)

式中：C代表空间域上任意一点的浓度；Nm为等参单元的形函数；Cm为等参单元的第m个节点浓度；Hm为等参单元的第m个节点总水头；M为8。

根据Galerkin有限元计算方法与隐式差分方法分别对空间域、时间域进行离散，得到有限元计算格式，如式(25)所示。

(25)

其中：

[DC]=

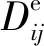
3.2 计算方法

3.2.1 协调质量矩阵处理

对于时间域离散，笔者曾采用过显式差分法、中心差分法、隐式差分法3种方法，计算过程中发现：

(1)采用中心差分格式与显式差分格式时，只能选取较小的时间步长，才能保证数值计算结果的稳定性，若时间步长过大，单元部分节点将出现无意义的负浓度。另外，这2种格式均不能有效地减少数值振荡问题。

(2)采用隐式差分格式，对减小数值振荡具有较为显著的效果，而且不会因时间步长的变大节点出现无意义的负浓度，但时间步长较小时，也会出现较大的数值振荡现象。

综合考虑，为避免在小时间步长下出现数值振荡，笔者在隐式差分格式离散时间域的基础上，采用集中质量矩阵代替协调质量矩阵，即对式(25)中的[DC]进行处理，具体处理方法详见文献[16]。

3.2.2 程序实现

采用FORTRAN语言进行程序设计，矩阵元素统一采用一维数组存储，对矩阵应用稀疏矩阵行压缩存储方案，线性方程组求解采用超松弛预处理共轭梯度法(SSOR-PCG)。

4 数值验证

本文分别对文献[6]中一维加速溶蚀试验、文献[17]中二维加速溶蚀试验开展三维数值模拟，通过数值模拟结果与试验结果、有限差分法计算结果进行对比，验证三维模型及有限元计算程序的正确性。

4.1 一维溶蚀模拟

引用文献[6]中的加速水泥净浆接触溶蚀试验资料，进行数值模拟。试件尺寸为40 mm×40 mm×20 mm，水灰比为0.35，在标准条件养护10个月后，采用6 mol/L的NH4NO3溶液进行加速水泥净浆试块溶蚀试验。

假设初始时刻的试块孔隙中充满孔隙液，且孔隙液中钙离子浓度为饱和浓度，如式(26)所示。基于本文所建立的数学模型，根据文献中的试验条件给出边界条件，如式(27)所示，相应的边界条件示意图如图2所示。

C(x,y,z,t0)=Csatu。

(26)

(27)

图2 边界条件示意图Fig.2 Schematic diagram of boundary conditions

通过水泥水化模型计算可得到试块中C-S-H与Ca(OH)2的摩尔含量，加速溶蚀过程中的固液平衡关系曲线其他参数取值与文献[6]相同，如表1所示，模型计算其他参数如表2所示。

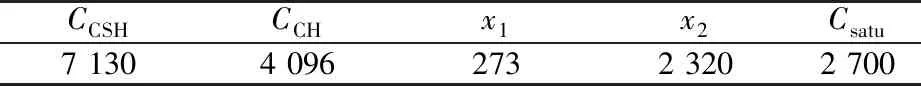
表1 固液平衡曲线参数Table 1 Parameters of solid-liquid equilibrium curve mol/m3

表2 模型计算基本输入参数Table 2 The basic input parameters of FEM program

注:kT取值参考文献[18]。

图3(a)为本文模拟的溶蚀深度与文献[6]试验数据及有限差分法模拟的结果对比，从图3(a)可知，本文模拟(FEM)结果与有限差分法模拟(FDM)结果具有较好的一致性，两者与试验结果在试验前期吻合较好，后期具有一定的误差；经分析，这可能是由于经过一段浸蚀时间后，溶蚀介质NH4NO3溶液浓度有所降低，减缓了试件溶蚀进程[6]。

图3(b)—图3(d)分别为本文计算结果与文献采用有限差分法计算结果的对比情况。从孔隙液钙离子浓度分布、固相钙浓度分布及孔隙率分布3个方面对比可知，本文模型计算结果与文献[6]模拟结果具有较好的一致性。

图3 模拟溶蚀特征量与文献[6]数据对比Fig.3 Comparison between modeling the spatial distributions of characteristic variables and the data from Ref.[6]

4.2 二维溶蚀模拟

引用文献[17]中的接触溶蚀试验资料，对试验中水泥净浆试块进行加速溶蚀数值模拟。试验中水泥净浆试块尺寸为10 mm×10 mm×2 mm，水灰比为0.5，采用6 mol/L的NH4NO3溶液进行加速水泥净浆溶蚀试验。由于试件上下侧与骨料接触，本文假设试件这两侧不与NH4NO3溶液接触，即认为该试验为二维溶蚀试验。边界条件示意图如图4所示。

选取中间截面进行溶蚀深度分析，溶蚀深度随时间变化关系如图5所示，与文献[17]试验数据对比发现，本文模拟计算结果与试验数据吻合良好。

图4 边界条件示意图Fig.4 Schematic diagram of boundary conditions

图5 模拟溶蚀深度与文献[17]数据对比Fig.5 Comparison between modeling leaching depth and the experimental results from Ref.[17]

图6为溶蚀24 h后各溶蚀特征量分布云图，可以看出，固体钙浓度由内及外逐渐降低，溶蚀程度逐渐增强，与文献[17]试验结果对比发现，固体钙浓度分布与试验所到溶蚀分布具有较好的一致性。孔隙液中钙离子分布与固体钙浓度分布规律基本一致。需要指出的是，孔隙率分布规律与固相钙浓度分布规律正好相反，这是由于接触溶蚀是一个由表及里的发展过程，与内部相比，外部固相钙溶出量更大，孔隙体积增大程度更大。

图6 模拟溶蚀特征量分布与文献[17]试验结果对比Fig.6 Comparison between modeling the spatial distributions of characteristic variables after 24 hours and the experimental results from Ref.[17]

选取接触边界节点进行分析，其溶蚀特征量随时间变化关系如图7所示。从图7(a)可以看出，边界节点随着时间增加孔隙液钙离子浓度逐渐减小并最终趋于稳定；从图7(b)可以看出，固相钙含量变化呈现出相同的规律。这充分表明离子交换边界条件能够有效地避免采用“0浓度”边界条件造成的问题，即接触边界节点孔隙液中钙离子浓度始终为0，接触边界节点固相钙溶出过程瞬间完成。

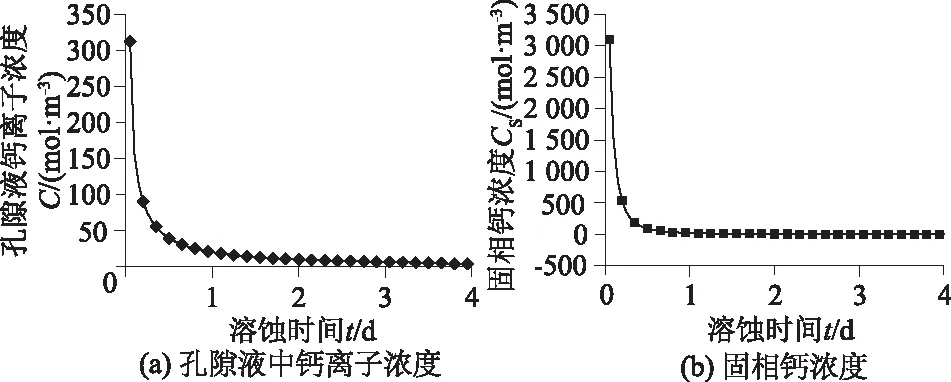
图7 边界节点孔隙液钙离子浓度、固相钙浓度随时间变化关系曲线Fig.7 Time-histories of calcium ion concentration in pore fluid and solid phase

通过数值模拟结果与试验数据、有限差分法模拟结果对比可知，各项溶蚀特征量数据吻合良好，本文模型及程序的正确性得到验证；采用离子交换边界条件能够有效避免“0浓度”边界条件造成的问题。

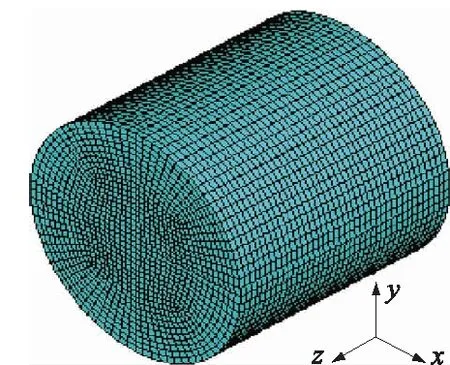
图8 试件5有限元模型Fig.8 FEM model of specimen 5

5 算例

5.1 模型简介

目前溶蚀试验研究大多以一维、二维展开，三维较少涉及，因此，本文给出一个三维溶蚀的数值算例，研究三维溶蚀下的各溶蚀特征量的空间分布规律。考虑一个圆柱体水泥净浆试件，尺寸为Φ20 mm×20 mm，将其置于6 mol/L的NH4NO3溶液中，使试件与溶液充分接触；水泥化学组分及其他模型计算基本输入参数取值见表1、表2；试件的有限元模型如图8所示。

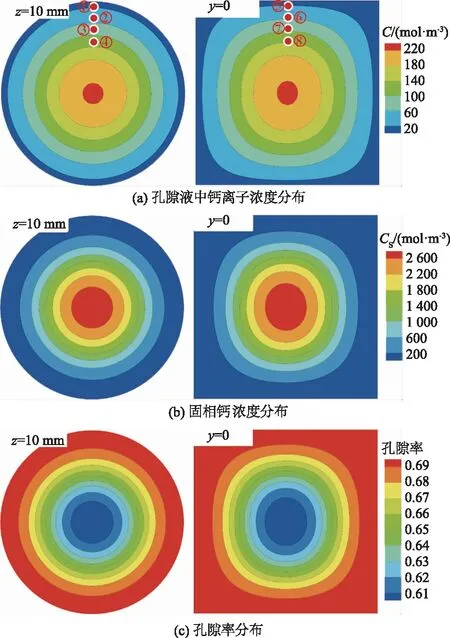
图9 各截面溶蚀特征量模拟计算结果Fig.9 Modeling results of characteristic variables at each section

5.2 结果分析

为了研究溶蚀的空间分布规律，选取y=0 mm和z=10 mm 2个截面展开分析。经过40 d溶蚀后，各截面的各溶蚀特征量模拟计算结果云图如图9所示。从图9可以看出，无论是径向还是轴向，各溶蚀特征量的空间分布规律与上文算例呈现出一致的规律。

为了研究各溶蚀特征量随时间的变化规律，在试件径向取4个特征点，分别距离表层为1，2，3，5 mm，编号依次为①,②,③,④；在试件轴向，以试件顶面圆心为基点，从上至下取4个特征点，分别距离表层为1，2，3，5 mm，编号依次为⑤,⑥,⑦,⑧。根据计算可得，各溶蚀特征量与时间的变化关系，如图10所示。可以看出，随着时间的变化，特征点的各溶蚀特征量变化速率均呈现出由快变慢的总体规律，说明各处的溶蚀速率由快变慢；从图10(b)可以看出，固相钙浓度在7 000 mol/m3左右时，溶蚀速率开始变慢，这是由于此时Ca(OH)2溶解完成，C-S-H开始溶解，而C-S-H前期的溶解速率远远小于Ca(OH)2的溶解速率。无论是径向还是轴向，各个特征点开始溶蚀的时刻均不相同，呈现出外部早于内部的总体规律，体现出接触溶蚀是一个由表及里的过程。需要指出的是，在径向与轴向上，距表层距离相同的特征点的溶蚀开始时间并不相同，径向明显早于轴向，据分析，这是由于所选取的径向特征点所在处的浓度梯度大于轴向特征点，从而造成孔隙液中钙离子径向扩散速率大于轴向扩散速率。

图10 各截面特征点孔隙液中钙离子浓度、固相钙浓度、孔隙率随时间变化的变化关系曲线Fig.10 Time-histories of calcium ion concentration in pore fluid and solid phase and porosity at feature points