地形地貌条件对边坡动力响应规律的影响
2019-11-13唐为民1马淑芝刘小浪
唐为民1,马淑芝,刘小浪,赵 轩
(1.贵州省交通规划勘察设计研究院股份有限公司, 贵阳 550081;2中国地质大学(武汉) 工程学院,武汉 430074)
1 研究背景
我国是一个多山多震、地质地理条件独特的国家,由地震诱发的崩塌、滑坡等斜坡地质灾害问题较为严重[1]。近年来我国经济飞速发展,国家高瞻远瞩地实施了西部大开发战略,大量的公路铁路、水利工程等基础设施建设正在西部地区开展,而西部多是高烈度的山区,工程边坡稳定问题历来非常严重。而由于边坡在地震作用下的失稳机制与只在重力作用下有很大不同,所以研究地震作用下的边坡稳定性十分必要。充分认识地震作用下斜坡的动力特性,研究地震作用下斜坡动力变形破坏机制,不仅能推动地震边坡稳定性理论的发展和创新,而且能够有力指导抗震减灾和灾后重建等工作,具有十分重要的理论研究意义和工程实践意义。
地震作用下边坡稳定性的研究已经有很长历史,常用的地震稳定性分析方法如拟静力法、滑块分析法和数值分析法已经取得了大量研究成果[2]。但由于动力学问题的复杂性,这些方法往往存在局限性,因此,研究结果的可靠性也有待验证。模型试验方法是一种校验其他分析方法正确性和进行边坡地震稳定性分析的有效手段,模型试验包括振动台模型试验和离心机模型试验。目前国内离心机设备资源稀缺,尚存在较多技术问题未解决,在边坡地震模拟研究中取得的成果较少[3];而振动台模型试验因其规模大、可重复性好、直观性强等优点成为研究人员常采用的一种模型试验方法。汶川地震以来,已经有越来越多的学者就岩土边坡地震稳定性问题进行振动台试验研究,取得了大量研究成果。徐光兴等[4]设计完成了比尺为1∶10的土质边坡振动台模型试验,探讨了地震作用下模型边坡的动力特性与动力响应规律。许强等[5-6]设计完成了一系列大型边坡模型的振动台试验,系统研究了强震诱发地质灾害的成因机理。陈新民等[7-8]设计完成了振动台试验,研究了下蜀土边坡地震稳定性。Srilatha等[9]对不同加筋量条件下的土工格栅和土工布模型边坡进行了一系列的振动台试验,研究了加筋方式和加筋量对模型边坡动力响应的影响。但相对于岩质边坡,目前在土质边坡动力特性和动力响应方面的研究尚少。
本文对土质边坡进行概化处理,设计并完成了土质边坡动力特性与动力响应的振动台模型试验。试验考虑土质边坡的地形地貌条件,分析了地震作用下土质边坡动力特性和动力响应变化规律。
2 振动台模型试验设计
本次振动台模型试验利用中国地质大学(武汉)三峡中心地震动模拟实验室大型两轴向电液伺服地震模拟振动台进行,振动台如图1所示。振动台台面尺寸为100 cm×200 cm,台面最大负载为250 kg,台面满载情况下最大位移为±100 mm,最大加速度为20 m/s2。本次试验是文献[10]中土质边坡振动台试验的进一步研究,关于试验设备、模型边界条件的处理、模型制作及传感器的埋设等相关内容已在文献[10]中有所阐述,为避免重复相同内容,此处不再赘述。

图1 地震模拟振动台Fig.1 Shaking table used in the test
2.1 相似律设计
受实验室条件限制,目前的振动台试验大多只能进行缩尺模拟,因此模型与原型之间的相似律设计十分重要。相似律规定了相似的模型与原型间必须满足的条件,又确定了将试验数据推算到原型上的换算法则,使得实验室条件下研究原型的物理规律成为可能[11]。当然,绝对严格的相似律难以实现,试验时需要根据试验研究目的和实验室条件,考虑主要因素,完成相似律设计,指导试验进行。
在土体边坡振动台模型试验中,地震动力作用下模型和原型分别满足的基本单值条件包括几何条件、物理条件、运动条件、动力平衡条件及边界条件。相似律设计中以边坡尺寸l、加速度a和边坡土体密度ρ作为控制量,在相似第三定理的基础上,采用相似转换的方法推导土体边坡振动台模型试验中模型边坡和原型边坡的相似关系。原型边坡不同高度条件下模型主要相似常数如表1所列。
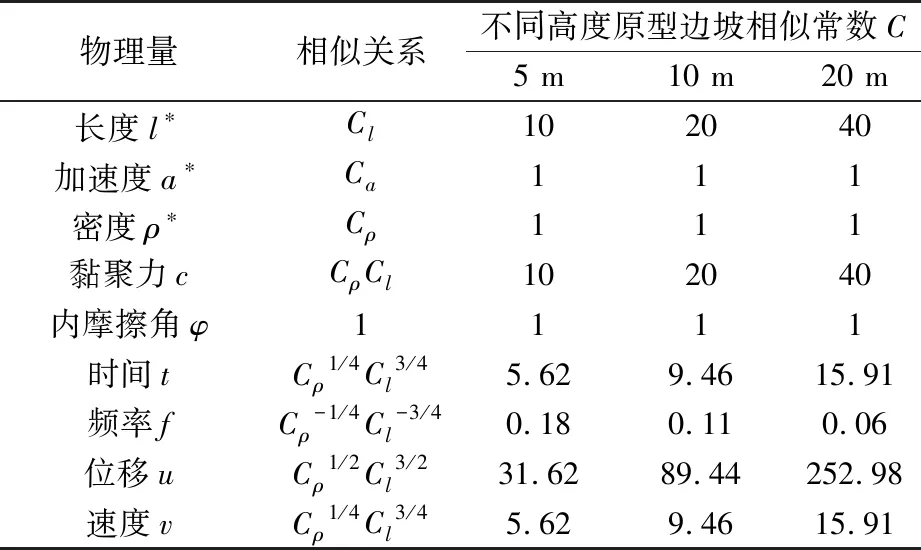
表1 振动台模型试验相似律Table 1 Similarity law of shaking table model test
注:Cl中C表示原型与模型间相似常数,下标l表示原型与模型间长度的相似系数。文中其他相似常数的意义类似;*表示控制量。
2.2 试验模型建造
边坡地形地貌条件是边坡地震稳定性的内在因素。本次振动台试验考虑边坡地形地貌条件,建立了多组土质边坡概念模型:建立了不同坡脚角度的直线型边坡,改变角度分别为30°,40°,50°,以考虑边坡角度因素;建立了凹形坡和凸形坡,与所建立直线型边坡一同进行试验,以考虑边坡坡面形态因素;建立模型边坡高度为50 cm,根据表1中土质边坡振动台试验中的相似律,改变输入地震波的时间压缩比分别为5.62,9.46,15.91即可对应3个尺寸的土质边坡,其尺寸相似常数分别为1∶10,1∶20,1∶40,以考虑边坡尺寸因素。
试验中边坡土体的相似材料由取自库区的淤泥质黏土、河沙以及重晶石粉、双飞粉、水等材料配制而成。模型土材料配比为m黏土∶m河沙∶m重晶石粉∶m双飞粉∶m水=2∶10∶5∶3∶2。试验中以密度ρ、黏聚力c及内摩擦角φ为模型土材料的主要控制参数。由表1可知,不同尺寸边坡所用模型土的控制参数密度ρ和内摩擦角φ的相似常数均为1,只有黏聚力c的相似常数相差数倍。而常见黏土的黏聚力一般在10~30 kPa范围内,不同尺寸边坡土体黏聚力相似常数Cc分别为10,20,40,相应模型土的黏聚力c都在1 kPa左右,其黏聚力相差不大。为了试验的便捷性和经济性,试验中只配置一种模型土来建立土质边坡模型,进行振动台模型模拟试验。原型和模型的主要物理力学参数列于表2,由于本次试验中所建立模型均为概念模型,没有具体的原型边坡作为参照,所以试验中原型边坡黏土物理力学参数参照《工程地质手册》[12]进行取值。

表2 土体的主要物理力学参数Table 2 Material properties of soil
关于模型成型方法和传感器的埋设要点已在文献[10]中有所阐述,模型制作和传感器安装布置如图2所示,建造好的模型如图3所示。
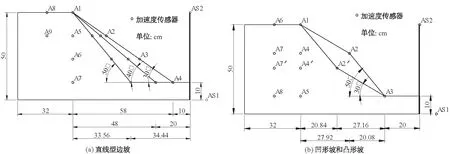
图2 模型边坡形态及传感器布置Fig.2 Slope shape and sensor arrangement of linear slope, concave slope and convex slope

图3 建成模型边坡Fig.3 Completed model slope
2.3 地震波加载设计
本次振动台试验过程中向边坡模型施加了不同类型、频率和振幅的水平方向地震波作用,主要有白噪声、EL波、KOBE波和WC波。在加载每一种地震波进行振动试验之前,首先进行白噪声扫描,白噪声加载时间为30 s,峰值加速度为0.30 m/s2,以测试模型的初始动力特性。随后依次向模型输入峰值加速度为0.63,1.25,2.5,5 m/s2的地震波,所加载地震波按照相似律设计的时间压缩比进行压缩。每级加速度施加完成后停止一段时间,对振后模型边坡进行观测记录,然后再施加高一级的加速度,直至边坡模型变形破坏。本次振动试验具体加载工况如表3所列,本文主要以不同形态边坡加载KOBE波为例进行动力分析,KOBE波加速度时程曲线如图4所示。
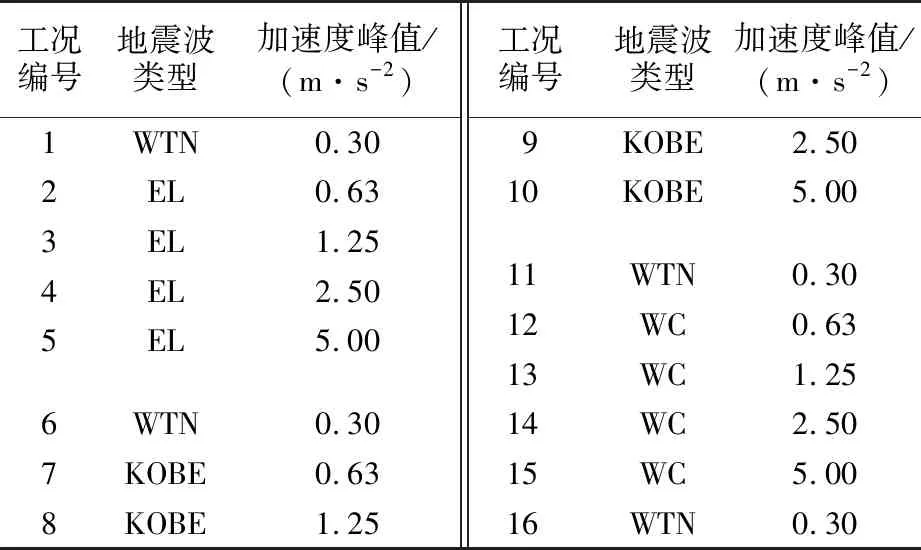
表3 地震振动台试验工况Table 3 Conditions of shaking table test
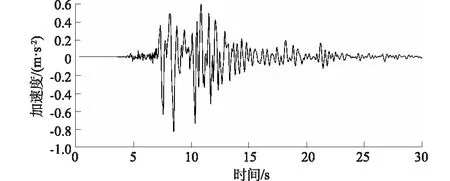
图4 KOBE波加速度时程曲线Fig.4 Acceleration time-history curve of KOBE wave
3 模型边坡加速度响应规律
已有研究表明,边坡失稳破坏主要是由与地震加速度有关的地震惯性力造成的[8],因此本文以边坡各监测点加速度响应值对边坡进行动力响应分析。为了研究边坡模型加速度动力响应规律,直线型边坡埋设A1—A9共9个加速度传感器;凸形坡和凹形坡中埋设8个加速度传感器。试验中在模型边坡底部输入不同参数的地震动荷载,通过埋设的加速度传感器监测动荷载作用下边坡不同位置加速度响应值。为便于分析,本文参考前人研究成果引入加速度峰值(PGA)放大系数的概念说明边坡对地震荷载的放大效应[4],此处PGA放大系数即为边坡内某一监测点所监测到的加速度峰值(PGA)与实际施加于边坡加速度传感器AS1所监测到的加速度峰值之比。依据试验中监测得到的数据进行分析,研究边坡地形地貌条件对边坡在地震动荷载作用下的响应规律。
3.1 模型边坡加速度响应规律
试验结果表明,不同地震工况条件下模型边坡加速度响应规律基本相同。现以对坡脚角度为40°的直线型边坡模型输入时间压缩比为9.46、PGA为2.5 m/s2的KOBE波为例进行动力分析,指出土质边坡模型加速度动力响应的基本规律,后面会进一步对不同地形地貌条件下土质边坡动力响应规律做出分析。图5为边坡模型在地震动荷载作用下不同监测点PGA放大系数随高程变化的曲线。
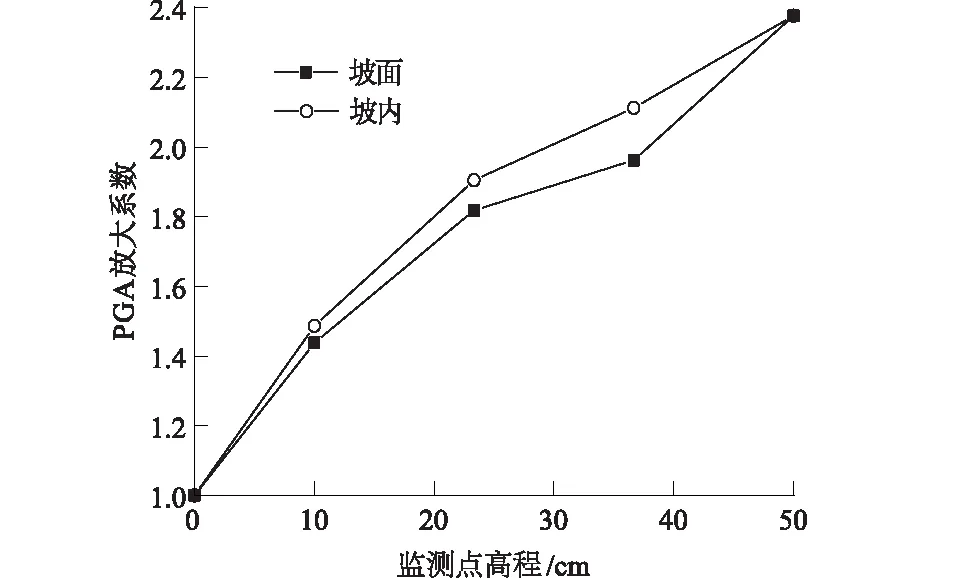
图5 模型边坡PGA放大系数随高程变化规律Fig.5 Change laws of PGA amplifications with elevations
从图5可以看出,地震作用下边坡加速度响应有着非常明显的高程放大效应。其PGA放大系数随高程增大表现出非线性增大的趋势,在边坡坡脚附近PGA放大系数随高程近似线性增大,在坡中附近增长趋势有所减缓,在靠近坡顶位置又急剧增加,坡顶位置PGA放大系数达到2.4左右。对比模型边坡坡内和坡面加速度响应情况,可以知道不同高程加速度沿水平方向上的响应规律基本相同但并不完全一致,总体上坡内加速度放大效应比坡面更加显著,同一高程边坡坡内加速度响应要比坡面位置更大。
3.2 坡高对加速度动力响应规律的影响
根据振动台试验相似律设计,对模型边坡输入时间压缩比为5.42,9.46,15.91的地震波时,振动台试验中模型边坡分别对应着坡高为5,10,20 m的原型边坡。这种设计方式使得试验中不需要建造多个尺寸的模型而只要改变输入地震波的时间压缩比就能够模拟不同尺寸的原型边坡,大大节省了试验时间和试验成本。现以对坡脚角度为40°、输入时间压缩比为5.42,9.46,15.91、PGA为2.5 m/s2的KOBE波的直线型边坡模型为例进行动力分析,指出原型边坡高度对土质边坡模型加速度响应规律的影响。图6为不同高度原型边坡在地震动荷载作用下坡面加速度响应变化规律。
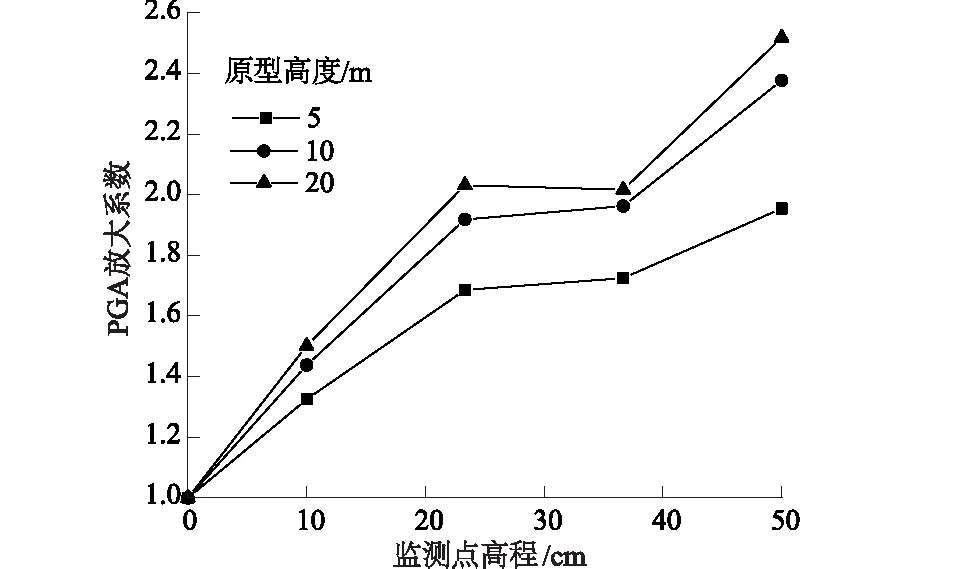
图6 不同原型高度模型边坡PGA放大系数 随高程变化规律Fig.6 Change laws of PGA amplifications with elevations of model slope with varied height
从图6可以看出,不同原型高度模型边坡坡面各高程点PGA放大系数随高程变化规律基本相同。同时可以看出,随着原型边坡高度的增大,PGA放大系数也随之增大。原型边坡高度为5 m时,边坡各高程点PGA放大系数较小,甚至在坡肩位置也只有2左右,远小于边坡高度为10 m和20 m之时。当边坡高度增大,边坡各高程点PGA放大系数也随之增大,但边坡高度为10 m和20 m时,PGA放大系数增长趋势已经有所减弱,说明PGA放大系数不会随着边坡高度增大一直增长。总的来说,动荷载作用下土质边坡加速度放大效应表现出随边坡尺寸增大而更为显著的趋势。
3.3 坡度对加速度动力响应规律的影响
现以输入加速度峰值为2.5 m/s2、时间压缩比为9.46的KOBE波的不同坡脚角度直线型边坡例进行动力分析,指出边坡坡度对土质边坡模型加速度响应规律的影响。图7为不同坡度边坡在地震动荷载作用下坡面加速度响应变化规律。
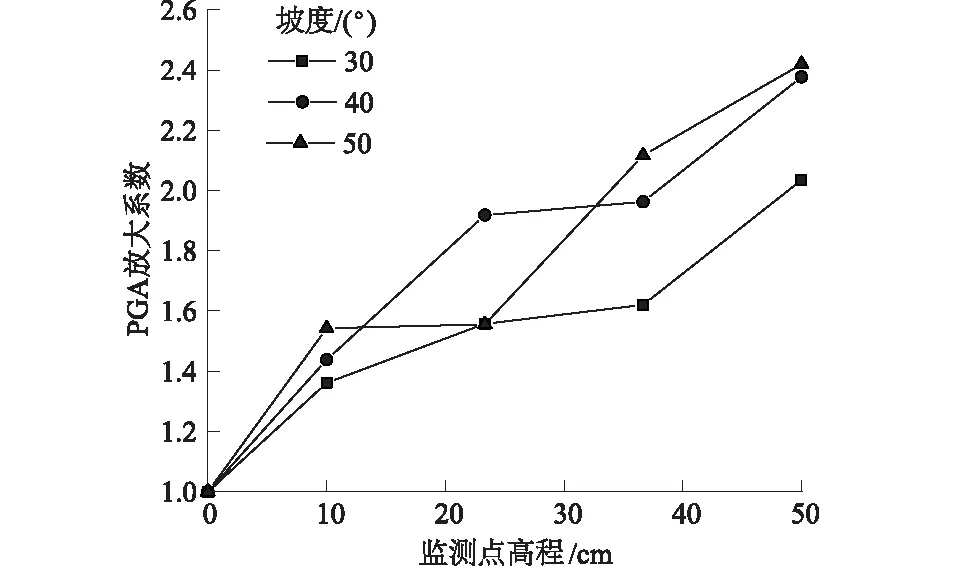
图7 不同坡度模型边坡PGA放大系数随高程变化规律Fig.7 Change laws of PGA amplifications with elevations of model slope with varied slope angle
从图7可以看出,不同坡度模型边坡坡面各高程点PGA放大系数随高程变化规律基本相同。同时可以看出,随着模型边坡坡度增大,PGA放大系数也随之增大。边坡坡度为30°时,各高程点PGA放大系数较小,甚至在坡肩位置也只有2左右。当边坡坡度增大,边坡各高程点PGA放大系数也随之增大,但当边坡坡度为40°和50°时,PGA放大系数增长趋势已经有所减弱,说明PGA放大系数不会随着边坡坡度增大一直增长。
总的来说,动荷载作用下土质边坡加速度放大效应表现出随边坡坡度增大而更为显著的趋势。
3.4 坡形对加速度动力响应规律的影响
现以输入加速度峰值为2.5 m/s2、时间压缩比为9.46的KOBE波的不同坡面形态边坡为例进行动力分析,指出边坡坡形对土质边坡模型加速度响应规律的影响。图8为不同坡面形态边坡在地震动荷载作用下坡面加速度响应变化规律。
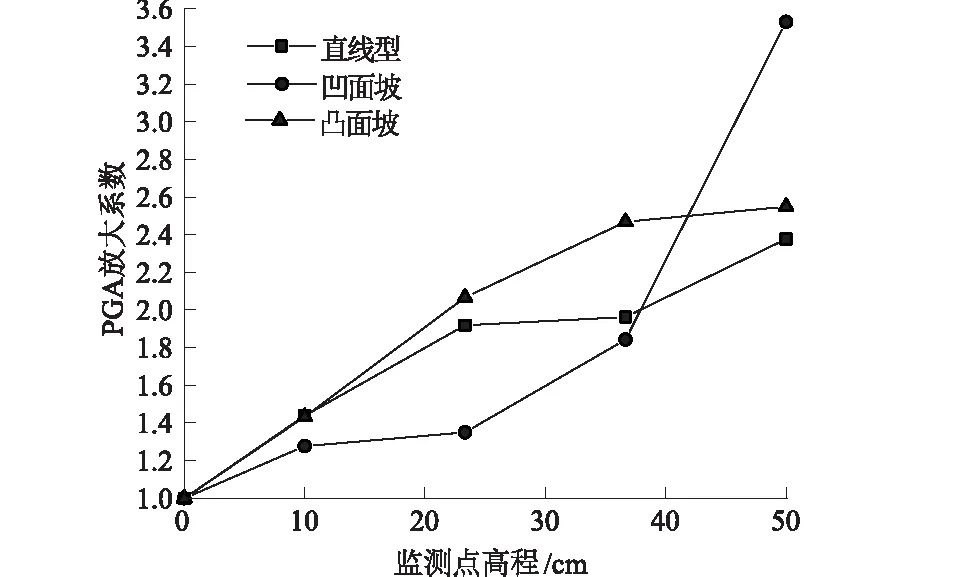
图8 不同形态模型边坡PGA放大系数随高程变化规律Fig.8 Change laws of PGA amplifications with elevations of model slope with different shapes
从图8可知,不同形态模型边坡坡面各高程点PGA放大系数随高程变化规律基本相同。同时可看出,坡形较为复杂时边坡PGA放大系数也较大,与凸面坡和凹面坡相比,直线坡对地震波放大效应更小,其PGA放大系数随高程变化也不如凸形坡和凹形坡剧烈。在边坡坡面转折部位以上,凹面坡PGA放大系数远大于直线坡和凸面坡。边坡形态越复杂时其对地震波放大效应越明显,这是因坡形较为复杂的边坡应力集中的部位也多,边坡更容易出现破坏变形。
4 坡体宏观变形
在对土质边坡加载地震波进行振动台模型试验时,观察到了边坡模型的变形破坏现象,边坡坡顶及坡体内部产生了一系列土裂缝,当输入地震波震级较大时边坡出现滑移破坏。由于土体颗粒之间黏结力有限,土质边坡在地震力作用下会在边坡内部形成微裂缝,地震波会在这些微破裂面附近发生反射、折射,表现为边坡内部地震放大效应大于坡面,并使得这些微裂缝进一步发展。边坡坡体内部所产生的裂缝主要是由微裂缝发展而来的横向拉张裂缝以及由拉张裂缝向下发展而成的拉剪裂缝,裂缝的规模与加载于边坡的地震波振幅有关,从宽度<1 mm的微小裂缝到5 mm左右的大裂缝均有出现。当地震震级较小时,边坡基本不出现破坏变形,偶有在边坡后缘坡顶软弱面或坡肩转折面附近形成较小的拉裂缝(图9(a))。当地震震级加大时,微小拉裂缝由于持续的地震力作用开始扩展,在边坡坡面2/3处至坡肩位置以及坡顶靠近坡肩位置附近出现宽度1~2 mm、延伸长度为10 cm左右的较大裂缝,边坡坡体也开始出现破坏变形(图9(b))。地震震级继续加至最大,变形体产生剪切滑移破坏,斜坡失稳,边坡坡面出现滑移破坏(图10)。

图9 边坡裂缝Fig.9 Cracks on slope

图10 边坡滑移破坏Fig.10 Slip failure of slope
改变边坡地形地貌条件的土质边坡振动试验结果表明,边坡地形地貌条件对边坡变形破坏有较大影响,其结果从侧面证明了土质边坡地震动力响应规律的正确性。试验结果显示:边坡坡度越大,坡体的变形破坏迹象越明显,边坡坡度为30°时,坡体的变形破坏迹象并不明显,坡体中只是出现了一些规模较小的裂缝,甚至当地震波振幅增至最大也只在边坡表面出现少量裂缝,发生失稳破坏的情况较少;在试验时边坡的失稳破坏主要发生在边坡坡度为40°和50°的边坡上,坡体的变形破坏现象明显,在这个坡度范围内即使边坡没有发生失稳破坏,坡体中也产生了较大规模的裂缝。坡面形态对边坡变形破坏有较大影响,凹面坡较于直线型边坡和凸面坡,坡体的变形破坏迹象不太明显,发生失稳破坏的情况比较少,但凹面坡坡体上部通常会有较大的坡体滑移现象;凸面坡最易发生失稳破坏,坡体中出现的裂缝规模也比较大,坡体在坡面转折部位会发生规模较大的破坏变形。
5 结论与展望
本文根据边坡地形地貌条件设计并完成了一系列土质边坡振动台模型试验,试验中对边坡模型输入不同类型、不同幅值的地震动荷载,通过对模型边坡进行动力反应及宏观变形方面的研究,探索了边坡地形地貌条件对土质边坡动力响应规律的影响以及边坡地震反应机理。得出了以下结论:
(1)土体边坡地震动力响应具有高程效应,PGA放大系数会随着高程增加而增大,且水平方向上边坡坡内较坡面对地震动荷载放大更为显著。
(2)地形地貌条件是影响土体边坡地震动力响应的重要因素,边坡高度越高,边坡坡度越大,边坡形态越复杂,其对地震动荷载放大效应也越明显,边坡变形破坏也越大。
(3)在地震力作用下土质边坡坡内附近会形成微裂缝,地震波会在这些微裂缝附近被放大,并最终使这些微裂缝发展为张拉裂缝。拉裂缝在持续地震力的作用下不断发展,最终使变形体产生剪切滑移破坏,导致边坡失稳,发生变形破坏。
地震力作用下边坡的动力行为十分复杂,总结本次课题积累的经验,边坡在地震力作用下的动力响应规律还需要进一步研究:
(1)后续试验应在相似材料的配制方面做出更多改进,以更加严格地满足模型与原型之间的相似律,使试验结果更加可靠。
(2)水是影响地震作用下边坡稳定性的关键因素,此次试验未考虑地震力作用下边坡中孔隙水压力的作用。在后续试验中应该制作密封条件更好的模型箱,增设水压力传感器以研究地震作用下孔隙水压力在边坡动响应中的作用。
(3)在后续试验中,应结合地震作用下各类工程边坡问题对影响边坡地震稳定性的因素进行针对性的深入研究,以指导地震风险山区的防灾减灾及灾后重建工作。
