基于加权均分模型的学生入学差异性效应分析

刘丽峰，王志勇，郭 兵

(山东理工大学 建筑工程学院, 山东 淄博 255049)

目前, 大学课程考试中，按照基础知识占60%，中等难度占20%，提高部分占20%的比例分配，该分配比例既能检查学生普遍对基础知识掌握情况，又能了解学生课堂内知识的综合应用、课堂外知识的加深及自我提高能力，相对应的考试成绩也一般呈正态分布，即大部分学生能够掌握基础知识，也有一定的综合应用能力，成绩位于中等水平，一部分基础水平较好且课下认真钻研的学生成绩优异，相应剩余的学生上课不认真学习会出现不及格。但是近几年来, 由于定向委托培养及边缘地区分数线照顾等因素, 使得同一班级的学生学习水平有较大的差异，但这部分学生所占的比例较小，尚且对成绩整体分布影响不大，因此总体来说考试成绩仍然服从或近似服从正态分布，即成绩很高或很低的人数所占比例较小，成绩中等的人数比例较大[1-4]。文献[5]采用工商管理专业的高等数学成绩进行分析，证明了学生成绩符合正态分布。文献[6]的研究表明凡符合教学规律的考试,其总体成绩应服从或接近服从正态分布。文献[7]阐述了学生成绩未必要服从正态分布的观点。文献[8]的研究表明非智力因素对高职院校学生英语成绩正态分布有着很大的影响。文献[9]利用混合正态分布来拟合学生的成绩分布，并进行实证分析。

刘应成[10]论述了在考试系统中成绩正态分布检验的设计与实现方法。郑月锋等[11]提出了一种将成绩修正为正态分布的算法, 可以在维持原始成绩排名的基础上调整成绩, 使得它符合正态分布。高义中等[12]从Fuzzy集合的角度来分析学生群体在某门课程考试结果中，其成绩服从正态分布的置信度问题。但同时也要兼顾到入学基础水平的差异、统计个数较少等因素的影响，有些成绩服从偏态分布[13-15]，因此在教学评估、学生成绩评定和教学管理工作评估等方面的以正态分布评估就存在一定的局限性。为了对教师教学、学校教学质量和教学管理等工作进行更为科学的评估，有必要在主体为正态分布的情况下，考虑入学基础水平差异,本文采用加权均分模型进行成绩分析。

1 加权均分模型原理

正态分布是目前成绩分析的常用模型，然而影响考试成绩的因素具有多样性，目前国内外学者从多方面对影响学生考试成绩的因素进行了研究：(1)在教学环境方面，Ilana等[16]、Chan等[17]阐述了学生借助先进的自学条件能够提高学习的效率和效果；(2)在班级总体状况方面，Tomáš等[18]、Benot[19]等的研究表明性别对考试成绩影响有明显的差异，Erika 等[20]的研究发现班级总人数对学习成绩较差的部分学生成绩影响较明显；(3)在学生个体学习差异方面，李莹[21]的研究表明个体学习风格对高等数学的成绩影响不显著，李金屏等[22]则研究了学生个人的学习时间和学习效率对学生成绩影响。以上研究没有考虑学生入学基础知识的差异对学习效率的影响，本文在教学环境一定的情况下，研究学生个体入学基础差异和就业形式两个因素对考试成绩的影响。在成绩分布模型构建方面，借鉴孙毅等[23]多元线性回归分析方法建立考试成绩评价与预测的回归模型。为提高计算效率，在对学生考试成绩分布拟合中，采用对数分布模型。

本文成绩加权均分模型构建的思路为：建立入学成绩影响因素学号N(由于学生学号一般按照入学成绩高低由小到大排列)和就业形势影响因素招生人数NT为自变量，拟合成绩yN为因变量的对数模型，即

yN=a2ln(NT+C1+a1*N)

(1)

式中：C1为避免(NT+a1*N)过小或趋于0，而使得对数值过大而取的常数，本文中C1值取2；a1为入学基础水平影响系数;a2为基台系数。

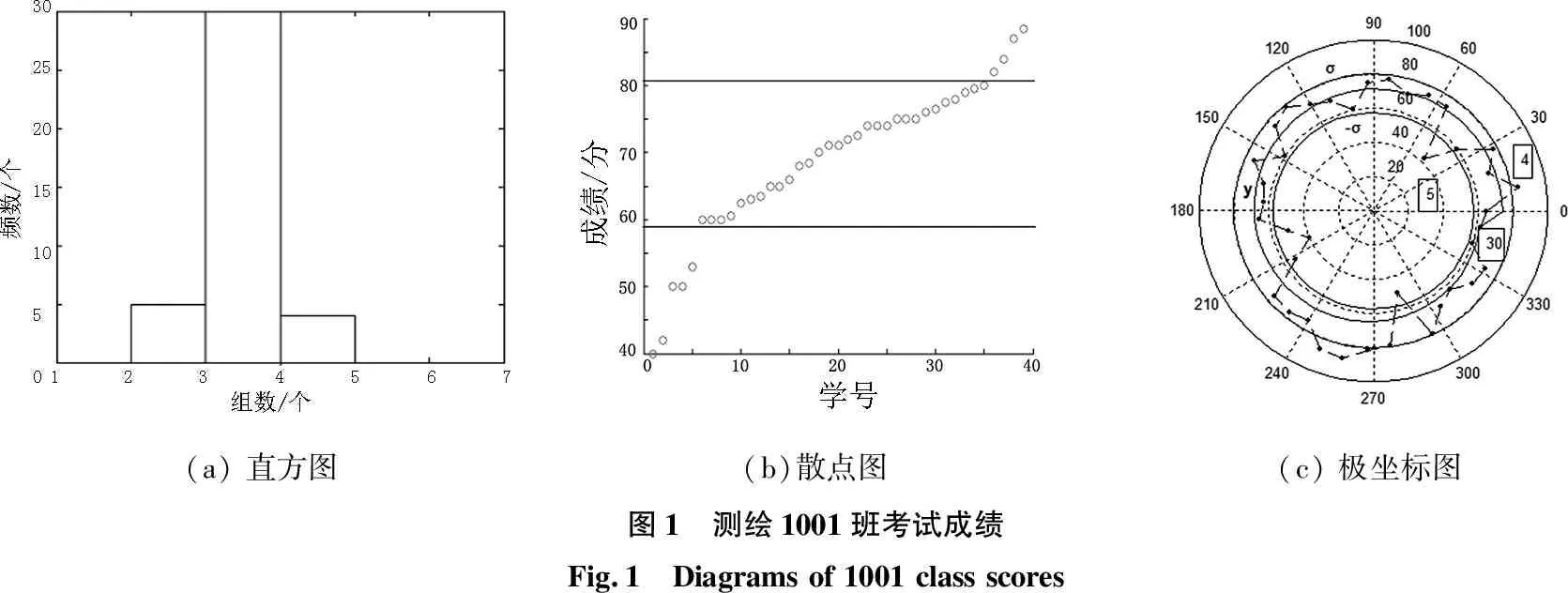
(a) 直方图(b)散点图(c) 极坐标图图1 测绘1001班考试成绩Fig.1 Diagrams of 1001 class scores

基于正态分布的思想，采用拟合成绩趋近于标准成绩，介于一倍标准差之间的数据占68.26%，大于σ的成绩为优异，小于-σ的位于60分左右，即不及格(小于60分)或没有绩点(大于60分但小于70分)。以测绘1001班为例，为便于比较成绩的优劣，将成绩按照由低到高的顺序进行排列，以一倍标准差为限值将成绩分为三类，分别绘制直方图、散点图和极坐标图，如图1所示。由图1(c)可以清楚地看到每个学生成绩的分布情况，可以弥补正态分布在学生成绩个体差异显示方面的不足。

2 加权均分模型的构建

为简化成绩加权模型，在式(1)中，分析一个班级成绩加权模型时，该班级的人数NT为固定值，且C1也为常数2，因此可以将NT+C1由常数C代替，式(1)可简化为

yN=a2ln(C+a1N)

(2)

将式(2)进一步分解为

(3)

式中:yN，N，NT分别表示加权均分模型的拟合值、学号和班级总人数;a1为入学基础水平影响系数，a1绝对值大小表示影响的程度。

式(3)进一步改写为基台值Bv和系统变化值Sv之和，即：

yN=Bv+Sv,

(4)

Bv=a2lnC，

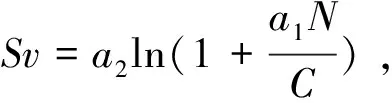
当a1符号为负时Sv为递减函数(即Sv1>Sv2>…>SvNT，当C不变时，Bv不变，则y1>y2>…>yNT)，表示入学基础水平对考试成绩有正影响，学习状态良好；反之a1符号为正时属于不正常状态；而a1为0时，表示所有学生的学习成绩相同，这是不存在的；Bv的意义为理论上学号为0的考试成绩，即为班内入学成绩理论上限值，Bv=a2lnC>0;而lnC=ln(NT+2)恒大于，故a2恒大于0。a2为基台系数，当a1>0 时，Bv为低基台，a2称为低基台系数；反之a1<0，Bv为高基台，a2称为高基台系数，在班级人数相同时，基台系数反映班级的极值变化情况，由此可以推导出yN取值范围为

图2表示了入学基础水平影响系数a1、基台系数a2和考试成绩关系，图2(a)为a1>0和a2为低基台系数的情况，图2(b)则表示a1<0，a2为高基台系数时的情况，图2(c)表示低基台系数小于高基台系数，图2(d)表示低基台系数大于高基台系数，图2(e)表示低基台系数等于高基台系数，y1=a12ln(C+a11N),y2=a22ln(C+a21N)。

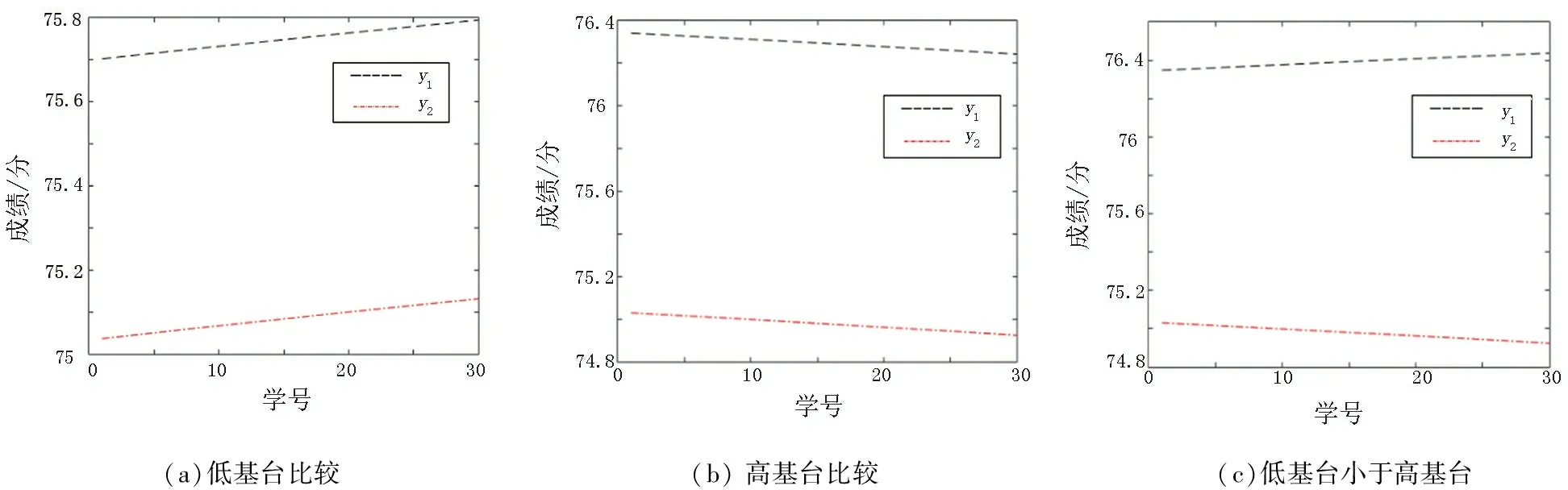
(a)低基台比较(b) 高基台比较 (c)低基台小于高基台

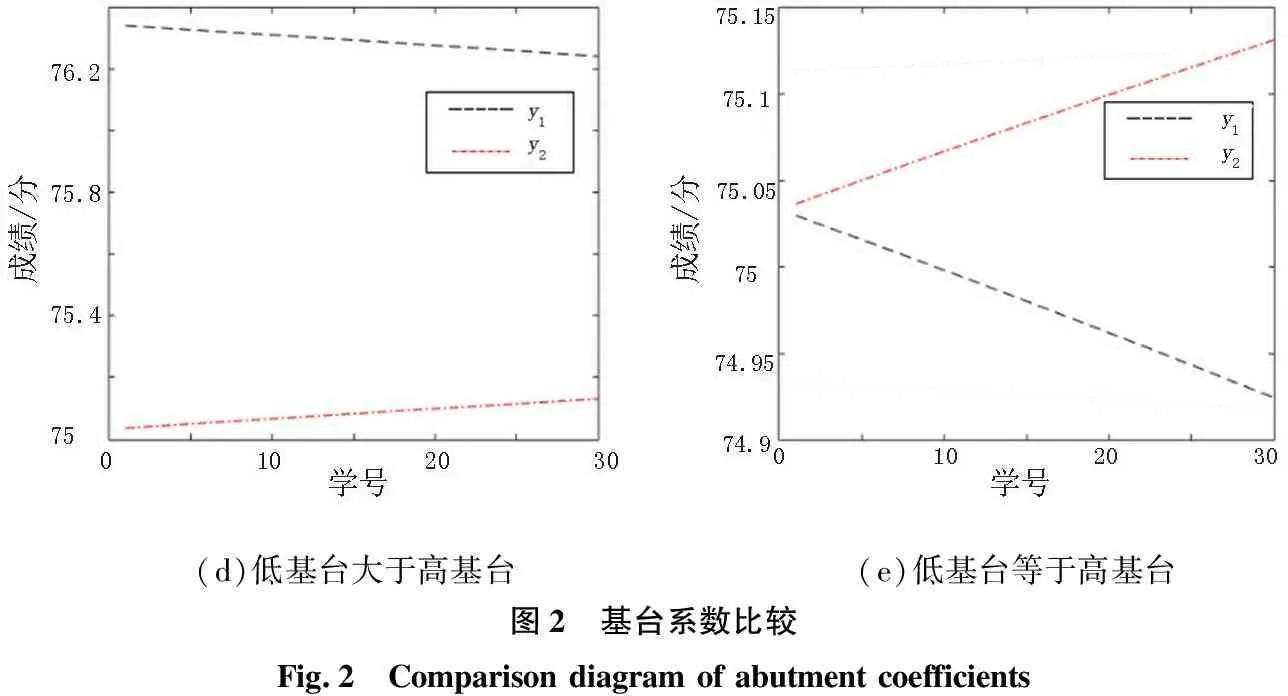
(d)低基台大于高基台 (e)低基台等于高基台图2 基台系数比较Fig.2 Comparison diagram of abutment coefficients

为比较加权均分模型与正态分布的关系，类似正态分布将考试成绩和相应的模型拟合值由小到大排列，并对班级成绩标准化(类似于正态分布，由标准化后的考试成绩所包围的扇形面积之和为1)后，绘制在极坐标图中，由于一倍标准差区域内的成绩能反映68.26%学生的学习状况，该部分对研究整个班级学生的特点和成绩变化趋势有重要意义，因此，将该部分学生人数与班级总人数之比定义为点值比(PRV)。PRV表示的正态分布和加权均分模型分别如图3(a)、3(b)所示。

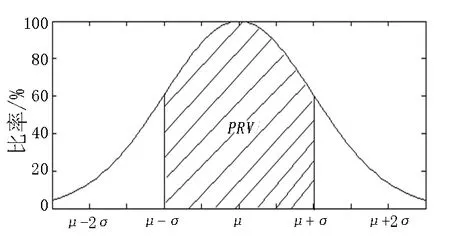
(a) 正态分布

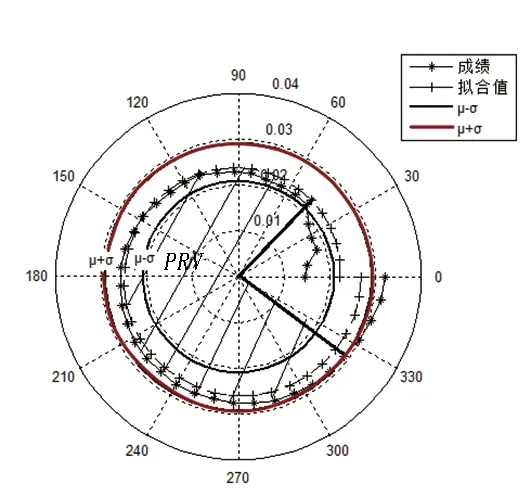
(b) 排序后极坐标图3 1001班考试成绩点值比的分布Fig.3 The score ratio distribution of examination results of class 1001

图4 1001班考试成绩直方图和极坐标图转换示意Fig. 4 Schematic diagram of histogram and polar coordinate transformation of class 1001 examination results

3 实证分析

下面以山东理工大学不同学年、不同专业、全班或部分学生的考试成绩进行实证分析：2008级城市规划专业1个班级CAD考试成绩、2008级测绘工程专业3个班级部分学生的计算机地图制图原理与算法基础考试成绩、测绘工程专业2009级与2010级3个班专业英语考试成绩和2012级2 个班级地图学考试成绩、2015级勘查工程专业1个班级测量学考试成绩。这些试题根据教学大纲、考试大纲进行规范化命题, 基本上基础知识占总成绩的60%，加深和提高部分占40%，一般学生考试成绩在70以上，总体要满足正态分布的要求。

验证的实例中包含专业基础课程(计算机、英语)和专业应用课程，下面分别针对这两种类型课程进行实证分析。

3.1 专业基础课程实证分析

计算机类专业基础课程包括班级全部都参与实验和部分学生参与实验，拟合结果如下：

全部参与的计算机类专业基础课程有城市规划专业2008级2班的CAD课程，共有39人，加权均分模型拟合函数为yN=ln(NT+2+N*0.38)* 16.53，拟合的点值比FPRV为0.68，拟合成绩均值为66.67，与实际考试成绩的差值为2.58，与正态分布的一倍标准差内密度函数积分(即正态点值比NPRV)0.68的比值为0.99，可见两者是非常接近的。

部分参与的计算机类专业基础课程有计算机地图制图原理与算法基础课程，2008级测绘工程专业1班21人、2班19人和3班11人，拟合函数和计算结果见表1。

由表1可以看出，即使有部分学生选课考试的成绩加权均分模型拟合得到的FPRV与正态分布的

表1 计算机地图制图原理与算法基础考试成绩拟合结果
Tab.1 The fitting of examination scores for course principle and algorithm basis of computer cartography

班级拟合函数拟合均值/分平均成绩/分FF/N0801yN=ln(NT+2-0.11∗N)∗ 20.6566.763.60.71.00802yN=ln(NT+2+0.42∗ N )∗ 22.3063.271.90.60.90803yN=ln(NT+2-0.37∗ N)∗ 29.6972.770.40.71.0

NPRV之比(F/N)仍近似等于1，平均误差仅为4.51%。比较表1中加权均分模型系数a1可以看到，0801班和0803班的a1小于0时，拟合均值成绩较高，说明考试成绩仍按照入学成绩分布状态排列，学习成绩较好的学生大部分没有出现大幅度下滑，班级整体学风保持较好，但0801班a1绝对值小于0803班的，表示0801班学生间考试成绩差异小于0803班的，且0801班平均分较低也说明了0801班整体学习成绩低于0803班的，而0803班学习成绩好的同学进步快，而学习成绩差的进步较慢，但成绩差的学生占较小比例；而0802班则出现相反的情况，说明该班学习状况出现异常，由于该课程开课时间为大四上半年，即第7学期，跟研究生考试及找工作时间冲突，0802班学生选择就业找工作人数较多，在一定程度上影响了学习成绩。比较3个班的基台系数可知，1班选修学生的学习状况较3班的差，1班的高基台系数20.65小于2班的低基台系数22.30，说明1班学生的学习状态比2班的差，而2班的低基台系数与3班的高基台系数进行比较，可以看到两者有一定交集，但总体来说3班仍有一部分学生较2班差，因此平均成绩稍微低于2班的。

鉴于以上实证结果，部分选课成绩与全班学生考试成绩都参与实验结果是一致的，因此英语类专业基础课程仅考虑全班参与的情况，选择2009级和2010级测绘工程专业1班、2班和3班的专业英语全班进行实验，分别有38人、40人、36人和39人、35人、35人，实证结果见表2。

由表2可得,成绩加权均分模型拟合得到的FPRV与正态分布的NPRV的平均误差仅为7.53%，两者近似相等，且绝大部分拟合FPRV都略小于正态分布的NPRV，这由于正态分布计算结果为精确值，而加权均分模型拟合值为近似解。比较2009级和2010级学生专业英语考试的成绩可以看出，2009级的FPRV与NPRV之比的平均值0.90较2010级的0.97低, 但两者相差3.27%；两者的平均值也存在相同状况，2009级平均分68.97比2010级的71.87相差4.20%，说明了2009级考试成绩低于2010级的。比较2009级入学基础水平影响系数a1：1班和3班的同为负号，且1班a1的绝对值小于3班的，而2班的为正值，这与表1的情况相同； 2010级则呈现出与2009级相反的状态：1班和3班的a1同为正数，1班a1的绝对值大于3班的，且1班的平均成绩72.7略高于3班的72.0，1班的基台系数a2小于3班的，表明1班和3班考试成绩与入学成绩相比出现异常，出现入学成绩差学生整体反超的现象，1班学生考试成绩差异较大，成绩下降的学生出现在入学成绩优异学生内，且少数的成绩存在较大幅度的下滑，3班也存在类似现象，但跟1班相比下滑幅度不大；而2班学生的考试成绩与入学基础有相同的趋势，但从较低的平均分70.9和基台系数19.90可以看出，虽然考试成绩符合其入学基础水平，但也表现出整体班级学习不甚努力的趋势，存在学生对专业英语的重视程度不够现象。

表2 专业英语考试成绩拟合结果
Tab.2FittingresultsofprofessionalEnglishtests

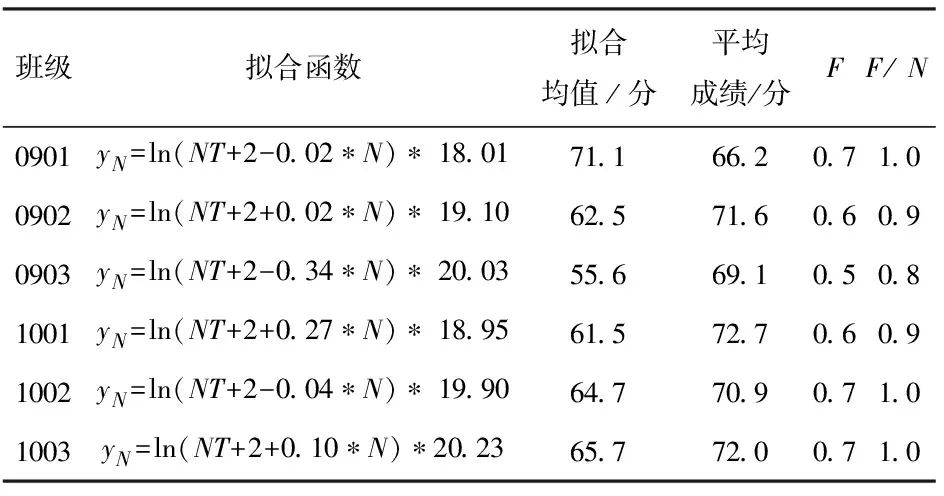
班级拟合函数拟合均值/分平均成绩/分FF/ N0901yN=ln(NT+2-0.02∗N)∗ 18.0171.166.20.71.00902yN=ln(NT+2+0.02∗N)∗ 19.1062.571.60.60.90903yN=ln(NT+2-0.34∗N)∗ 20.0355.669.10.50.81001yN=ln(NT+2+0.27∗N)∗ 18.9561.572.70.60.91002yN=ln(NT+2-0.04∗N)∗ 19.9064.770.90.71.01003yN=ln(NT+2+0.10∗N)∗20.2365.772.00.71.0

由于2009级和2010级学生的考试试题不同，因此不能直接比较平均分，但比较a1绝对值均值可以看到，2009级的0.13小于2010级的0.14，说明了2010级学生间成绩波动较大，而比较2009级和2010级的a1符号可以看到，这些波动是由于2010级整体学生成绩提高造成的，尤其是入学成绩较差的学生考试成绩的提高，也表明2010级学习风气较好及专业英语课程通过努力学习提高较容易。

3.2 专业应用课程实证分析

专业课程的实证包括了不同专业的两门课程：测绘工程专业选择了2012级1班和2班的地图学课程，两个班全部学生都参加了考试，考试的人数分别为1班40人、2班36人；勘查工程专业选择了2015级1班的测量学课程，全班34人的考试成绩进行实证，实验结果见表3。

表3 12级地图学和15级测量学考试成绩拟合结果
Tab.3FittingresultsofCartographyscoresfromclass2012andSurveyscoresfromclass2015

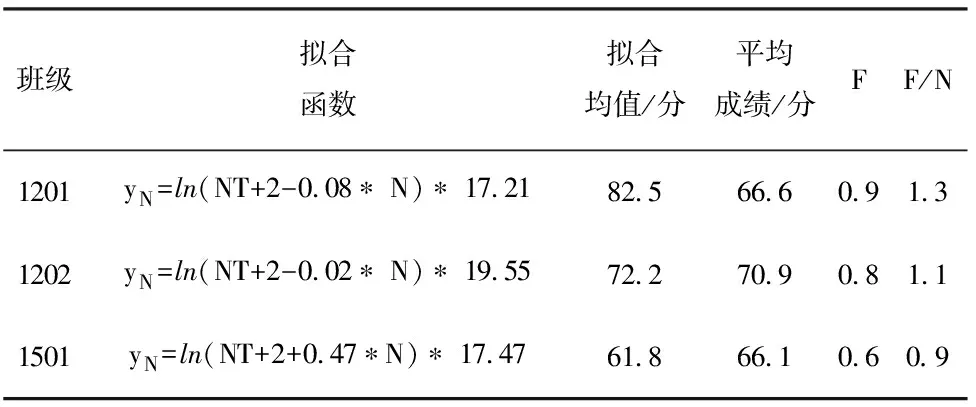
班级拟合函数拟合均值/分平均成绩/分FF/N1201yN=ln(NT+2-0.08∗ N)∗ 17.2182.566.60.91.31202yN=ln(NT+2-0.02∗ N)∗ 19.5572.270.90.81.11501yN=ln(NT+2+0.47∗N)∗ 17.4761.866.10.60.9

由表3可以看出，地图学成绩加权均分模型的FPRV略大于NPRV，而测量学考试成绩则相反；比较1201班和1202班的基台系数a2可以看到， 1班基台值小于2班的，因此1班学习状况较2班的差，且入学基础水平影响系数a1两者都为负数，但1班的绝对值大于2班的，说明成绩较差的学生学习更不努力。勘查1501班有正a1且平均成绩不高，说明了入学成绩较好的学生学习不认真，但入学基础差的小部分学生学习努力。表3加权均分模型系数a1与表1呈现相同的规律：a1小于0时拟合均值较高，表3同属于大二时开设的专业课，由于与地图学相比，测量学课程基础理论知识较简单，受入学基础成绩影响较小，入学成绩较差的学生只要认真学习极易反超入学成绩较好的学生，而入学成绩好的学生不认真学习时成绩下滑厉害，但入学成绩差的学生由于基础知识水平的限制，提高远不能抵偿下滑的成绩，而出现班级平均分不高的状况。

对比拟合FPRV与正态分布的NPRV关系图(见图5)，可以看出FPRV在NPRV直线上下波动，由此可得两者近似相等。通过比较开课的年级对考试成绩的影响(见图6)，2008级、2009级和2010级开课的年级都是大学四年级，学生的学习状态较为稳定，FPRV与NPRV的差值比大二选课的2012级、2015级的小，同时从图5上可以看到FPRV和NPRV在数值、变化趋势上都有很好的一致性和显著的相关性(皮尔逊相关系数为0.975，显著性p=0.000<0.01)。通过k均值聚类分析的结果也可以得到类似的结论，大四学生(2008级、2009级和2010级)分为一类，大二学生分为一类，而勘查2015级也由于基础较差被分到大四的类别中，之后对聚类结果的类别间距进行方差分析，方差分析表明，类别间距差异的概率值为0.004<0.01，即聚类效果好。也说明了加权均分模型与NPRV在大部分情况下拟合效果较好，但在个别课程上差异较大。

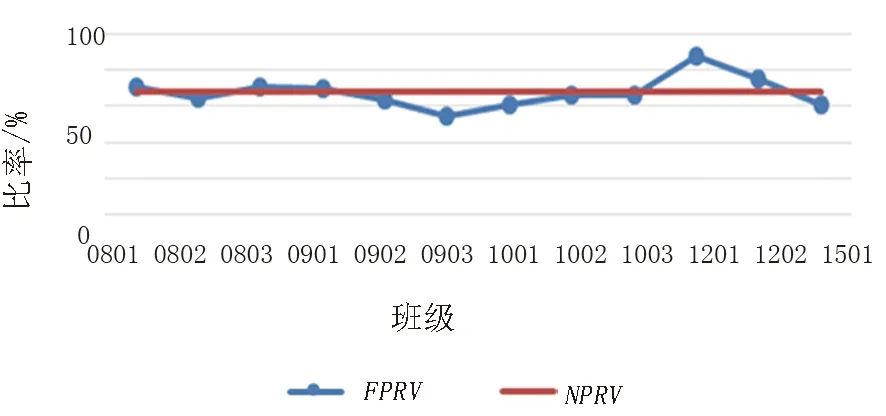
图5 考试成绩拟合FPRV与正态分布NPRV对比图Fig.5 Comparison diagram between FPRV and NPRV

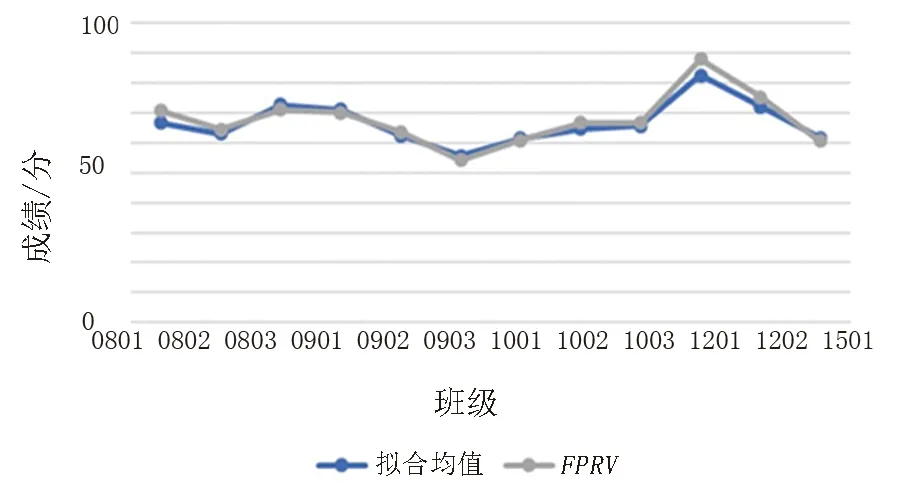
图6 考试成绩拟合均值与FPRV关系图Fig. 6 Relationship between fitting mean and FPRV of class examination results

4 结论

结合学生的期末成绩、选课情况、开课学期以及入学成绩，本文发现加权均分模型与正态分布模型在FPRV和NPRV方面有很好的一致性，同时开课学期对考试成绩有一定影响。在大四考研学期开设的课程中，与考研科目相关的(如专业英语)课程考试成绩平均成绩较高，而且也出现加权均分模型a1大于0，说明班级成绩整体提高，入学成绩差的学生提高更多；反之开设课程与考研内容相关不大时，则会出现考研对该门课程的负向影响，这时学生学习精力被考研分散，入学基础水平成为影响考试成绩的主导因素。由此可以得出结论：

1)在大四考研的学期内尽量安排与考研相关的专业课程，这不但可以提高学生学习的积极性，而且专业课的效率也能有较大的提高。

2)在大二阶段安排课程时需要考虑学生的基础水平、对课程的认识程度与专业的相关度等因素。

3)比较大四和大二阶段的平均分可以看到：大四阶段学生由于考研、找工作等因素对学习的影响，平均成绩较低，因此课程尽量少设置在该阶段。