基于t分布变异的飞蛾加权质心定位算法
2019-11-13毛永毅王晓甜
毛永毅,张 旸,王晓甜
(1.西安邮电大学通信与信息工程学院,陕西西安 710121;2.西安邮电大学科研处,陕西西安 710121)
0 引 言
无线传感器网络作为一种运用于目标追踪的全新的信息获取和处理技术,在与定位相关的研究领域有着非常广阔的发展应用前景。在地理环境监测、军事侦察、智能医疗相关的技术领域中,无线传感器网络更是作为其主要的支撑技术[1]。
在无线传感器网络中,目前所提出的定位算法分为基于距离测量和无需距离测量的定位算法。基于距离的定位算法是根据测量到的距离或者角度值的信息进行定位,主要有到达时间(Time of Arrival,TOA)、到达时间差(Time Difference of Arrival,TDOA)、到达角度(Angel of Arrival,AOA)等方法。无需距离测量的定位算法是根据网络连通性等信息实现节点定位,其主要方法有接收信号强度(Received Signal Strength Indication,RSSI)、质心定位算法、DV-Hop 定位算法等。与基于距离的定位算法相比,无需距离测量的定位算法不需要测量节点之间的距离。基于RSSI 测距技术因低成本、不需要额外硬件支持而广泛应用于室内的无线混合定位中[2-3]。
对于基于RSSI 的加权质心的混合定位算法,许多学者为了提高定位精度在权值构造上和引入优化算法两方面对整体定位算法进行优化。文献[4]提出一种RR-WCL 算法,该算法较传统加权质心定位算法在权值构造方面以未知节点到锚节点距离的比值作为权重来表示相应锚节点对未知节点的影响程度。文献[5]提出了一种基于PSO-GSA 优化的加权质心定位算法,利用PSO-GSA 优化算法对未知节点的坐标和定位模型参数进行整体优化。文献[6]在采集RSSI 的优化过程中采用卡尔曼滤波器,并在最后用锚节点的相关信息对四点质心定位算法的结果进行误差补偿。
本文提出一种基于t分布混合变异的飞蛾扑火的四点加权质心定位算法,即tMFO-FWCL 算法。在加权定位计算过程中利用新的权值构造策略初定位,然后利用这些初步定位坐标通过t分布混合变异的飞蛾算法进行优化。仿真结果表明,该算法较传统的加权质心定位算法、文献[4-5]和一般的飞蛾扑火定位算法在定位精度上有显著提升。
1 加权质心定位算法的改进
1.1 RSSI 测距
RSSI 测距是基于测距定位的第一个步骤,利用未知节点接收到的锚节点的RSSI 通过相应的信号传播模型对距离作估算。由于信号的发送天线存在方向性的问题,使得不同传输路径因环境不同进而导致了信号传播的不规则性[7]。信号的传输方式并非是理想的向四周扩散的圆形模型。目前主要的传输模型有RIM 模型、DOI 模型和Logarithmic Attenuation 模型。
Logarithmic Attenuation 模型是一种最典型的不规则信号传播模型,具体表达式如下:

式中:PR(d)是距离发送节点dm 的位置接收到的信号强度的均值,单位为dBm;Xσ~N(0,σ2)是信号强度的衰减部分,是一个服从标准正态分布的随机变量。
1.2 三角加权质心定位算法
确定了进行定位的节点坐标后,就可以进行加权定位。设三个圆心A,B,C的坐标分别为(x1,y1),(x2,y2),(x3,y3),对应的加权权值分别为ω1,ω2,ω3,通过RSSI 所得到的三个圆心到未知节点的距离分别为d1,d2,d3。通常情况下,将锚节点到未知节点通过衰减模型所换算的距离的倒数作为权值,具体的加权质心定位算法公式如下:
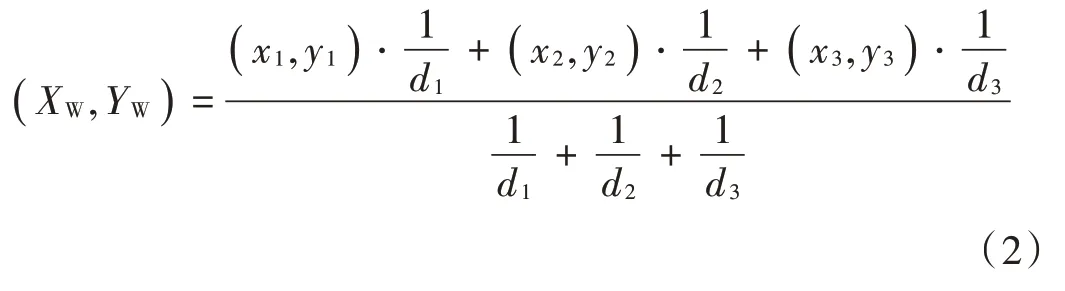
式中权值更加充分地利用节点测量信号强度和传播模型的信息,并且完善了权值的决定权,防止了过度修正[8]。
1.3 改进的四点加权质心定位算法(FWCL)
传统加权质心定位算法由于权值构造的不合理性往往使得定位误差较大。本文在文献[9]的基础上对于质心定位公式进行了改进。
在节点选择中,将得到的RSSI值根据相应的衰减模型计算出未知节点到各个锚节点的距离。按照距离值从大到小的顺序筛选出该未知节点所接收到的RSSI 值最大的4 个值。对于不能找出最近的4 个锚节点的未知节点,暂不进行定位。
对于上面能够找出最近的4 个锚节点的未知节点,对这4 个锚节点通过进行排列组合分成4 组,对于每组中的3 个锚节点利用改进的加权质心定位算法求出用于下一步定位的定位节点。改进加权质心定位公式如下:

式中:xi,yi为上步骤以排列组合后其中一组的3 个锚节点以锚节点坐标为圆心,以通信半径为半径所画出3个圆的交点的坐标值,如图1 所示。
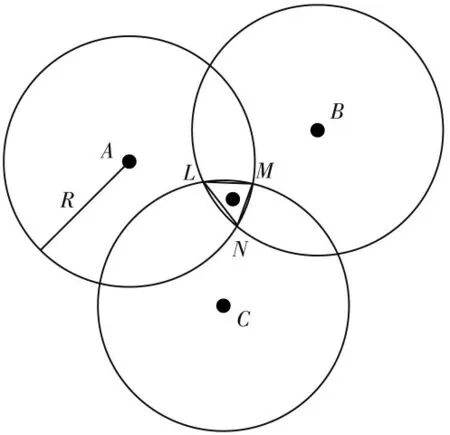
图1 加权质心定位算法的模型图Fig.1 Model diagram of weighted centroid localiazation algorithm
本文将权重ωi构造为:

其中:

式中:l为对锚节点进行分组的4 组中某一组的3 个锚节点距离未知节点的距离;n由文献[9]的结论将权重修正系数设为4。
对每一个分组利用式(3)最终得到4 个初步定位坐标值,再次利用这4 个初步定位坐标值代入到传统质心定位算法,得到改进的四组点加权质心定位的坐标值,完成第一轮定位。
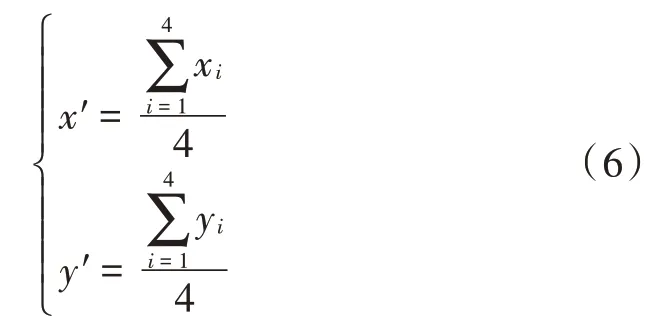
在对区域内可以进行定位的未知节点完成了首轮估计后,将定位后的未知节点纳入到锚节点中,对上面所提到的不能满足质心定位条件的未知节点重新定位,依次重复直到对该区域内所有的节点都完成定位。
2 基于t 分布变异的飞蛾扑火算法
为了解决质心定位算法的本身局限性和传播模型中η值受环境因素的影响这两个问题,本文在改进加权质心定位算法的权值构造的基础上,利用t分布混合变异的飞蛾扑火算法(tMFO)对定位结果坐标和η值进行优化。
2.1 MFO算法
MFO算法是一种新型的仿生群智能优化算法,该算法对飞蛾横向定位的方式进行模拟,并仿照飞蛾螺旋飞行的轨迹方式,利用螺旋函数模型对其进行更新进而对结果进行优化。由于其算法的易实施性和自身的鲁棒性,MFO算法被广泛应用到实际的最优化问题中[10]。
在MFO算法中,飞蛾作为候选解。飞蛾的位置矢量作为问题的变量。飞蛾通过改变位置矢量来实现在指定维数中的移动,其中飞蛾矩阵用M表示:

式中:n为飞蛾的数量;d为维数。相应的适应度矩阵为:

除了飞蛾矩阵,MFO算法中还需要有与飞蛾矩阵所对应的火焰矩阵。火焰矩阵通常用F表示,具体表达式类比于飞蛾矩阵分别表示为F和OF。
飞蛾和火焰均为候选解,它们的区别在于每次迭代中位置的更新方式。在解空间中,飞蛾是移动的实际主体,火焰为目前获得的最优值,可以作为搜索完成的标志。
完成初始化后,使用下面的公式来更新飞蛾的位置:

式中:Fj表示第j个火焰;M i表示第i个飞蛾;S是螺旋线函数,其表达式如下:
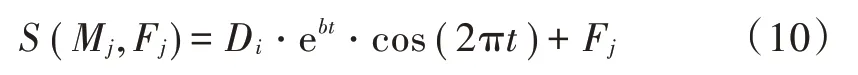
上述螺旋线模拟了飞蛾的飞行路径,并确定了飞蛾相对于火焰的下一个位置。其中:Di表示第i个飞蛾到第j个火焰的距离;t为[−1,1]的随机数;b为常数。Di的计算方法如下:

为了使算法以较快的速度收敛,利用自适应火焰数量更新机制,在迭代的过程中自适应地减少火焰数目。
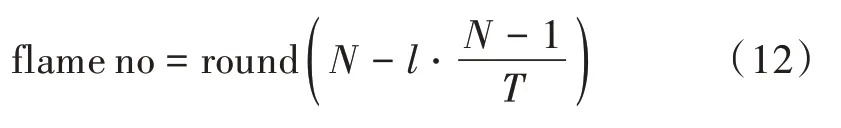
式中:N为火焰数量的最大值;T为最大迭代次数;l为当前迭代次数。
2.2 t分布混合变异
t分布的曲线具有左右对称的特点,并受自由度参数n的影响。当n=1 时,t分布的曲线与柯西分布曲线一致;当n>30 时,t分布曲线与正态分布开始重合;当n趋于无穷时,t分布曲线和高斯分布曲线开始接近。
飞蛾算法搜索时采用螺旋线波动模拟搜索模式,其螺旋线的相位采用随机游动的方式进行更迭,但是这种搜索方式在靠近极值点的情况时易受极值点干扰,最终导致被极值点吸引进而影响最终定位结果。而上述的t分布随着自由度的变换可以在柯西分布和高斯分布之间切换,高斯分布具有很好的全局开发能力;柯西分布具有很好的局部开发能力[11],因此可以利用t分布混合变异对飞蛾算法进行改进。本文对飞蛾的状态进行t分布变异:

式中:⊗为点乘;t(Iteration) 是以MFO算法迭代次数为自由度的t分布。式(13)表示在当前飞蛾个体空间的位置上增加了t分布随机干扰项M⊗t(Iteration) ,利用当前种群的信息来进行变异,并利用算法的迭代次数作为当前变异的t分布的自由度。较一般的MFO算法,基于t分布混合变异的飞蛾扑火算法利用t分布的特点,通过自由度的调整很好地兼顾了高斯分布和柯西分布的优点,进而将算法的全局探索能力和局部探索能力进行了很好的整合。
为了使算法的解进一步优化,这里对每一次迭代中飞蛾的最优位置进行高斯变异处理以提高解的质量。
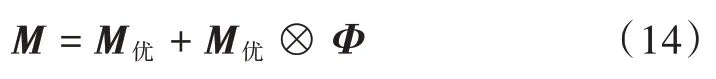
Φ是与M同阶的高斯分布矩阵。因此,整体算法的变异策略就是在飞蛾算法的每一次迭代过程中,对于最优飞蛾位置矩阵进行高斯最优变异,对于飞蛾最优位置之外的其他飞蛾采用t分布变异,这样有利于整个飞蛾的位置跳出局部最优解进行全局开发。
2.3 适应度函数构造
设未知节点的最终定位坐标为(x,y),定位后所得到的初步位置坐标为(x′,y′),τ为调节因子,则有:
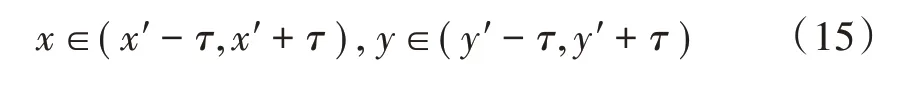
这里为了增加求解效率,τ的取值为10。
为了便于下面优化,将传播损耗模型的表达式进行简化,设d0为1 m,PT-PL(d0)为b,是常量,10η为a。简化后的公式如下:

最终,为了达到整体算法模型的自适应效果进而达到全局最优,这里构造适应度函数为:
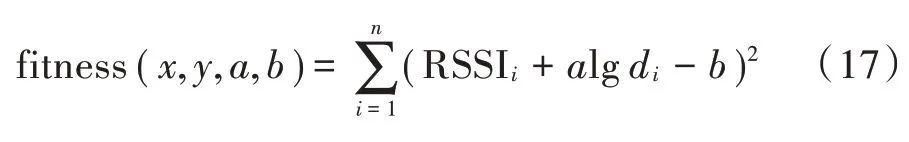
代入前面算法的初步定位坐标,可将式(17)右边改写为:
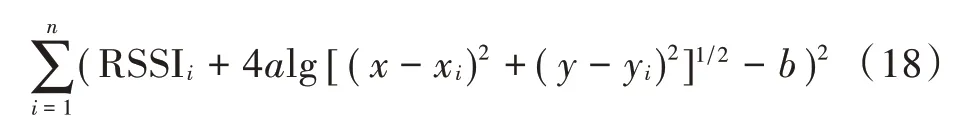
2.4 TMFO-FWCL 算法流程
TMFO-FWCL 算法流程具体如下:
1)利用FWCL 算法得到未知节点的最初定位坐标,作为飞蛾矩阵。
2)初始化飞蛾矩阵和火焰矩阵。
3)根据式(17)构造出适应度函数。
4)比较每只飞蛾的适应度值,取最小值。
5)利用式(10)更新飞蛾的位置和火焰矩阵。
6)利用上述t分布混合变异策略对每次迭代过程中的最优飞蛾和普通飞蛾分布进行不同的变异。再次比较,取最优位置赋给火焰矩阵。
7)判断是否达到迭代次数,若达到,输出最优解,结束算法;否则,返回到步骤2)再次计算。
8)结束迭代,找出全局的最优解、最优位置和最优参数。
9)计算平均定位误差,具体方法如下:
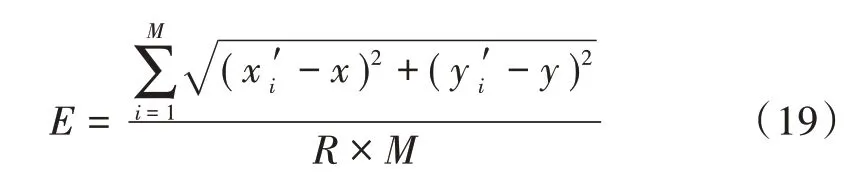
式中:M为未知节点的个数为未知节点的估计位置;(x,y)为未知节点的实际位置;R为节点的通信半径。
3 仿真分析
本实验平台采用Matlab 2015a,在100 m×100 m 的正方形区域内随机分布锚节点和未知节点的位置。该区域内未知节点的数目固定为100 个。节点部署的参数设置中锚节点的GPS 误差为0。其中,发送信号的功率为0 dBm,参考距离为1 m,距离参考节点处的信号功率为55 dBm,初始路径损耗指数η为4,所附加的高斯白噪声均值为0,方差为4。
在上述相同的仿真环境下,分别采用传统的加权质心定位算法、文献[4]中的RR-WCL 定位算法、文献[5]中基于PSO-GSA 的定位算法、结合飞蛾算法的MFO-FWCL算法和本文tMFO-FWCL 算法进行比较,并对其定位结果进行分析。
在MFO 的优化算法中,飞蛾数量N=50,式(10)中,b=1,维度d=3,最大迭代次数为100。
3.1 不同的锚节点数
图2 是随着锚节点数量的增加,5 种定位算法的平均误差变化曲线。

图2 不同锚节点数的定位误差曲线Fig.2 Positioning error curves from different numbers of anchor nodes
由图2 可知,当通信半径一样时,随着锚节点数量的逐渐增加,5 种定位算法的平均定位误差均逐渐减小,这是因为锚节点密度的增加使得可定位的未知节点数目增加所致。本文对于权值改进的MFO-FWCL 算法的误差低于文献[5]的PSO-GSA 算法的误差,再次改进后,本文tMFO-FWCL 算法平均定位误差在各个节点处均低于PSO-GSA 算法和MFO-FWCL 算法。平均误差分别相对提高了26.33%和12.67%。
3.2 不同的通信半径
当锚节点个数一定时,随着通信半径的增加,绘制5 种定位算法的平均误差曲线,如图3 所示。
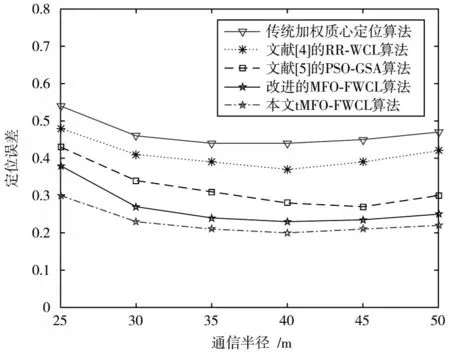
图3 不同通信半径的定位误差曲线Fig.3 Positioning error curves at different communication radius
由图3 可知,当锚节点的数量不变时,5 种算法的平均定位误差都是随着通信半径的增大而逐渐减小然后缓慢上升,这是由于起初随着通信半径增加会使整个定位环境的网络连通度提升,因而定位误差会减小;而后期过大的通信半径又会使平均定位误差增加。本文tMFO-FWCL 算法在任何半径的条件下定位性能均优于其他四种算法;经比较本文的算法较文献[4-5]的算法和MFO-FWCL 算法平均定位精度分别提高了39%,26.08%和13.67%。
4 结 语
为了解决质心定位算法定位精度差和MFO算法本身局限性的问题,在改进加权质心定位算法的基础上,采用基于t分布混合变异飞蛾扑火算法模型对定位坐标值进行优化,提高了定位精度。结果表明,tMFO-FWCL算法与一般的RR-WCL 算法、PSO-GSA 算法以及改进的MFO-FWCL 算法相比,能更有效地摆脱局部最优解,进而得到更高的定位精度。
