湿气混输管道瞬态输送数值模拟研究*
2019-11-12李志刚胡其会王红红王武昌肖文生王鸿雁
李志刚 胡其会 王红红 王武昌 肖文生 王鸿雁
1中海油研究总院有限责任公司
2中国石油大学(华东)山东省油气储运安全重点实验室
3中国石油大学(华东)机电工程学院
4青岛科技大学机电工程学院
我国在海洋、滩海和沙漠等区域探测到许多大型凝析气田,将这些油气资源输送到下游用户时一般采用两种输送方式:一种是把湿天然气在气体处理厂加工成凝析油和干气进行单相输送,这种输送方式需要在凝析气田附近建造大量处理设备,造成开采成本大幅增加;另一种是利用气井自身井口压力,将湿天然气混输至靠近下游用户的气体处理厂,分离成凝析油和干气,随管输压力和温度的变化,混输管道内产生凝析液和水[1],故湿天然气管道输送为多相管流,其涉及各相态间的质量和能量交换,给石油天然气工业生产带来严重的工程问题。
张友波等[2]采用实验数据对国外湿天然气管道的截面含液率计算关系式进行了验证评价。肖荣鸽等[3~4]对ARS相界面模型和MARS相界面模型进行了研究。尹鹏博等[5]对起伏湿气管路液塞速度特征数值模拟进行了研究。TAITE 等[6]建立了一维双流体模型。ANDRITSOS 等[7]预测分层波浪流的气-液界面摩擦因子时提出了一个经验关系式。BENDLKSEN[8]等建立了一个动态双流体模型,成功地应用于OLGA 软件。CHEN 等[9]提出一种双圆环假设。NICOLAS 等[10]提出一种计算界面摩擦因子的新关系式。Fan[11]建立了低含液量气-液两相流动实验设备,开展了低含液量气-油-水三相流动实验,建立了一个带有经验关系式的机械模型。DONG[12]建立了低含液量气-液两相流动实验设备,用实验数据对现有多相流模型进行评价。
目前对于低含液量多相流研究主要集中于低含液量气-液两相流动模型研究,对低含液量气-油-水三相流动模型的研究较少,现有的模型对湿天然气管道的低含液量水平适用性更差。国外对分层流进行了广泛的研究,但是仅限于低含液量分层流动的局部参数。
1 湿气混输管道瞬态输送水力计算模型
1.1 低含液量气液混输瞬态水力模型
采用双流体模型对多相瞬态流动进行模拟,它的唯一前提是假设介质是连续的,即认为某一局部点的质点微团仅在非常短的时间间隔内的流体动力性是不变的和均一的,满足局部瞬时特性。根据控制体内质量、动量和能量守恒,每相满足局部瞬时特性的微分形式守恒式,控制方程组可以用公式(1)统一形式表示

式中,ψk为单位质量介质的特性参数;ρk为密度;vk为速度向量;ξk为单位质量体积源;Jk为单位面积上的流出率张量。
表1列出了质量、动量和能量守恒方程中各对应量的表达式。

表1 质量、动量和能量守恒方程中各对应量的表达式Tab.1 Expressions of corresponding quantities in the equations of conservation of mass,momentum and energy
表1中pk为静压力;I为单位张量;Γk为剪切应力张量;qk为热流通量;bk为单位质量的体积力;Uk为单位质量介质具有的内能;为外界对单位质量介质的加热率;bk∙vk为体积力作的功。
相交界面是一个具有表面物理性质的空间几何面,界面上应满足质量、动量和能量守恒。假定气液界面是厚度趋于零的几何面,特性参数在界面两侧发生突变,故界面守恒特性又称为跃变特性或间断关系,满足局部瞬时特性的微分形式的守恒式可表示为公式(2)

式中:Δmk为从相k进入相界面的质量通量;vi为相界面的速度;nk为单位向量。
局部瞬时特性守恒方程描述了两相流的细微流动结构。为实现两相流动的理论分析和数值模拟,一般采用平均化方法得出宏观平均的两相流动方程和各种相间作用的表达式,但是平均化过程简化了流动描述,抹杀了流动细微结构的许多信息,导致宏观平均的两相流动方程不封闭[13]。另外,由该模型推导的两相流动方程形式复杂,难以直接求解具体流动问题,因此,实际求解时需引入合理的近似假设和正确的本构关系。采用的基本假设为:
(1)一维流动,忽略截面上参数分布的不均匀性,假设截面上各点压力、含液率、气液相流速相等。
(2)不考虑界面张力作用。
(3)忽略紊流脉动产生的应力。
(4)在计算单元内温度恒定。
这里采用的模型可以直接通过选取微元体,以双流体模型为基础,依据守恒定律推导出气相和液相的连续性方程。利用相界面上的质量交换间断条件可知,气相凝析为液相的质量流量等于液相蒸发为气相的质量流量,即Δmg=-Δml。对于油气两相管线,可利用闪蒸计算得到。气相和液相的动量守恒方程为
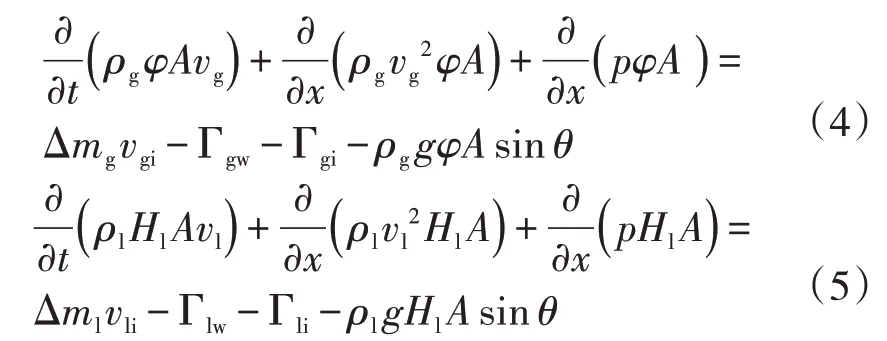
式中:φ为截面含气率;Hl为含液率;A为管道截面积;vg为气相速度;vl为液相速度;Δmg为气相凝析为液相的质量流量;Δml为液相蒸发为气相的质量流量;p为压力;θ为管线倾角;Γgw、Γlw分别为单位长度上气相和液相与管壁的剪切应力,与流型有关;Γgi、Γli分别为作用于气相、液相上的单位长度上界面剪切力,与流型有关;vgi为气相发生相变时的流速;vli为液相发生相变时的流速。当Δmg>0时,vli=vl;Δmg<0时,vgi=vg。
为闭合以上方程组,还需要一个气体状态方程

由此可得到气相中压力波的传播速度ag为

式中:p为压力;z为压缩因子;R为通用气体常数;T为温度。
对于式中各个参数的计算可参考前面的稳态模型中各个参数的计算,瞬态模型的流型判断参考前面流型模型中的气液流型判断准则。
1.2 边界条件和初始条件
根据特征线的定义,讨论双曲型方程的边界条件。现对方程在区域Ω()0 ≤x≤L,t>0内求解,已知特征值λ1>0,λ2<0,λ3>0,假定λ4<0,在边界x=0和x=L这两条直线上的4条特征线如图1所示。当特征线由解域内指向边界时,如x=0处特征线c2和c4,建立了一个由域内点函数值推算域边界点函数值的关系,这种特征走向不需要边界条件;当特征线由边界指向解域内时,如x=0处特征线c1和c3,建立了一个由边界点函数值推算内点函数值的关系,管线入口处需要给出2个边界条件。一般气液两相流管线的入口流量和出口压力已知,给定气相和液相流量,可联立求解出4个参数。已知出口压力与时间的函数关系,还需补充1个条件,可假设出口气液相速度梯度或含液率梯度为零。

图1 边界上的特征线走向Fig.1 Trend of characteristic lines on the boundary
为启动计算,须给定管线各点参数的初始值,可利用稳态计算值。根据两相流统一力学模型编制了稳态计算程序,在输入管线起点压力和气液流量之后,程序能够判别流型,计算管线各点的压力、截面含气率和气液流速,并存储在数据文件中,供瞬态程序调用。
2 瞬态混输模型实验验证
对低含液量气-油-水三相混输瞬态流动水力模型进行验证,验证内容包括实验验证与工程实际应用。
2.1 计算模型实验验证分析
2.1.1 低含液气液瞬态流动实验设计
将实验数据与模型结果对比,验证模型的准确性。实验时,在实验环道的试验段、距离气液混合器41 m 和200 m 的位置设置测压点P1和P2,分析实验环道在此两测压点的压力变化。实验流程如图2所示。

图2 多相流试验环道流程Fig.2 Flow of multiphase flow test loop
2.1.2 低含液气液瞬态流动模型的验证分析
通过比较气量、液量发生变化的瞬变过程,用管道内参数变化的实验结果和模拟结果来验证模型的精度。实验在0 ℃、1个标准大气压下进行,实验工况见表2。

表2 实验工况Tab.2 Experimental conditions
(1)气量增加过程。以实验1为例模拟气量增加瞬变过程,计算误差如表3所示。由实验结果可知,模型模拟计算P1和P2位置处的压力与实验测量的初末态压力之差的相对误差在10%以内,稳定时间相对误差在5%以内。
(2)气量减小过程。以实验2为例模拟气量减小瞬变过程,发现瞬态过程管内含气率的模拟值低于实验值,压力和含气率变化过程所用时间的计算误差如表4所示。
(3)同理进行了液量增加和减少瞬变过程实验,分别将位置P1、P2的压力模拟结果和实验结果进行了比较。瞬态压力变化模拟过程与实测过程接近,计算的终稳态压力P1和P2的相对误差均为5%。

表3 P1和P2位置处的压力计算误差Tab.3 Calculation error of pressure in P1 and P2

表4 压力和含气率变化过程所用时间的计算误差Tab.4 Calculation error of the time used in the process of pressure and gas content change
表5列出各工况下P1位置终态压力的实测值和计算值。表中瞬态计算值是由瞬态程序计算的终态压力值,稳态计算值是稳态程序根据终态的管线气液流量和出口压力直接计算出的压力值。比较结果说明计算值的误差很小,并且瞬态计算结果总体上好于稳态计算结果。
对于四种流量瞬变过程,本文建立的瞬态计算模型可以较好地预测集液量、集气量、起终点压力的变化,模型所采用的差分特征线算法具有较好的稳定性和收敛性,一定程度上解决了双流体模型算法易导致不稳定和不收敛的问题。
2.2 湿天然气长距离输送瞬态过程的模拟分析
由于管道起点供气量一般保持不变,而管道终点用户的用气量却随昼夜和季节发生变化,造成管道内气体储存量减少或增加。通过计算某管道凝析气输送过程,来模拟湿天然气长距离输送瞬态变化过程。管道为长30 km、直径12 in(1 in=25.4 mm)的水平管,假定管道起点流量保持1.3×106m3/d 不变,终点流量由1.3×106m3/d 分别逐渐增大到1.8×106m3/d 或减少到0.5×106m3/d,起点压力为6 000 kPa,流体温度为20 ℃,限定终点最低压力为4 000 kPa,限定起点最高压力为7 000 kPa。计算中时间步长取400 s,空间步长取3 000 m。
模拟分析时,首先进行初始工况稳态计算,以此计算结果作为初值进行动态计算。图3、图4分别为供气时集液量、集气量及起、终点压力随时间的变化规律。
图3为供气过程的管道内液体积聚量与储存气体量随时间的变化关系。可以看出,管道内的液体与气体量随着时间延续有逐渐降低的规律。在起始时刻,管道内的储气量变化较小,在供气期间,管道内有31 m3凝析液、15 178 m3气体供给终点用户。

表5 P1位置的终态压力实测结果与计算结果比较Tab.5 Comparison of measured results and calculated results of final state pressure in P1
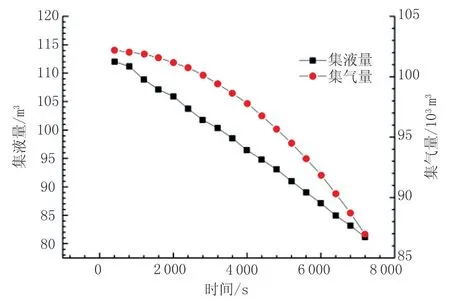
图3 供气时集液量与集气量随时间的变化Fig.3 Variation of the amount of liquid and gas collected over time during gas supply
从起、终点压力的计算结果(图4)可以看出,终点时刻压力相比起点时刻压力的下降幅度快得多;管道沿线压力降增大,由初始的771 kPa 增加为1 430 kPa。管道起点流量保持不变、终点流量增大,管道处于泄压状态,整条管线的压力都要下降,由于压力下降和管道终点的流量上升使管内气相流速增高,气液流速的增加使摩阻损失增大,压降上升。
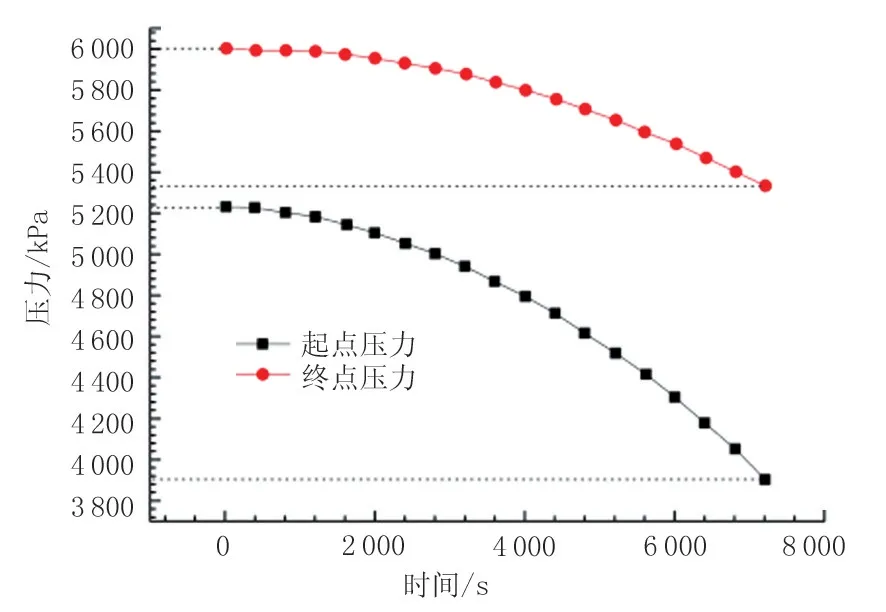
图4 供气时起、终点压力随时间的变化Fig.4 Variation of starting point and end point pressure over time during gas supply
对于储气过程,与供气过程类似,首先进行初始工况稳态计算,以此计算结果作为初值进行动态计算。图5、图6为储气时集液量、集气量及起、终点压力随时间的变化规律。
从图5可以看出,管道内的集液量与集气量随管道终点流量的降低不断升高,并有101 m3凝析液和16 177 m3气体储存于管道内。
从图6可以看出,终点压力的上升幅度比起点明显;而且沿线压降减少,在t=0时刻压力降为771 kPa,终点时刻压力降为343 kPa。原因是湿天然气管道与一般输气管道不同,湿气管道终点流量下降时管路内的积液量增多,如图5所示。

图5 储气时集液量与集气量随时间变化Fig.5 Variation of the amount of liquid and gas collected over time during gas storage
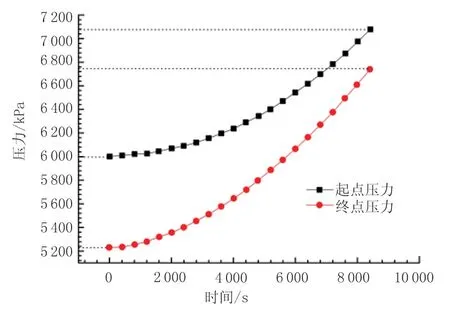
图6 储气时起、终点压力随时间的变化Fig.6 Variation of starting and endpoint pressure over time during gas storage
3 结论
(1)建立了低含液量稳态混输水力模型和气液混输瞬态模型,对湿天然气管道输送工况下的截面含液率以及压降进行计算。模型以双流体模型为基础,给出了随时间变化的质量、动量、能量等方程,并给出计算方法以及相应的边界条件和初始条件。
(2)对低含液气液瞬态流动模型进行验证分析,无论是在气量增加或减少过程,还是液量增加或减少过程,都与实验结果一致,说明模型准确可靠。
