多源数据融合在岩质滑坡监测预警中的应用

2019-11-12霍冬冬

四川轻化工大学学报(自然科学版) 2019年5期

霍冬冬，亓星

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610000；2.四川轻化工大学土木工程学院，四川自贡 643000)

引言

中国是一个地质灾害频发的国家，目前已经发现的地质灾害隐患点多达30万处，仅2018年已经发生2966起地质灾害，其中滑坡的发生率高达50%以上[1]。随着物联网技术的快速发展，多源异构传感器网络在滑坡监测中的应用越来越多，逐步替代过去传统的人工监测手段，开始发挥着重要的监测和预警作用[2]。基于物联网及云计算技术的发展，在地质灾害形成机理、预警判据研究的基础上，充分利用新一代信息技术在数据快速采集、传输上的优势，构建地质灾害实时预警系统，已成功对多处重大滑坡灾害做出了预警，不仅避免了人员伤亡和经济损失，而且也提升了人类面对自然灾害的处理能力[3]。在滑坡的预警模型研究方面，根据斜坡变形破坏的时间演化规律可将斜坡的变形破坏分为初始变形阶段、等速变形阶段和加速变形阶段，由此一些学者提出了根据位移-时间曲线的切线角进行滑坡预警，该方法后经许强的改进提出了一种改进的切线角作为滑坡预警的参考指标[4-5]。曾裕平通过对大量斜坡位移-时间的数据分析基于改进的切线角提出滑坡灾害蓝色、黄色、橙色、红色四级预警指标，该指标在实际滑坡灾害预警应用中发挥了良好的效果[6]。在滑坡监测应用中，为保障监测数据的完整性和及时性，对同一后缘裂缝往往会设置多个监测点，但是数据分析时却很少将所有监测数据进行融合处理，监测预警系统也是仅根据危险等级最高的一个监测点作为预警判据。根据单个监测点的数据分析来判断滑坡的整体稳定性，而单一监测数据很容易受到自然或人为因素扰动，有失科学性，从而造成预警信息误发。对大量异构、复杂的数据，可借助多源数据融合的方法提高数据的可信度并判断其正确性[7]。在多源数据融合理论模型的基础上，构建滑坡风险评估模型可以有效提高判断准确性[8]。本文提出一种多源数据融合处理方法，该方法基于多个监测点不同预警等级量化来判断滑坡是否进入临滑阶段，能够及时可靠地识别滑坡有效预警等级。

1 融合算法

基于多源数据融合的思想方法，对不同监测点的预警等级进行概率融合，得到判定滑坡是否已经处于临滑阶段的概率统计。

首先根据不同预警等级对于判断斜坡稳定性的重要程度分别赋予不同的权重，其次根据不同监测点位对判断斜坡稳定性逐个赋予权重，最后通过权重的计算可得到判断斜坡进入临滑阶段的概率，当此概率大于或等于50%时即可判定该斜坡已经处于临滑阶段。

1.1 预警等级的权重

监测预警系统将监测点所监测的滑坡位移变化量转化为参考指标，对危险滑坡进行阀值预警。由于监测预警只对事件发生可能性进行判断，不同预警等级可理解为对滑坡危险程度加以判断。基于以上考虑，可采用层次分析法，确定不同预警等级对滑坡危险性的判断。

层次分析法(analytic hierarchy process ,AHP)是一种实用的多属性决策方法。它能够通过比较不同因素对于某一事件的重要程度，计算得到这些因素对于解决问题的权重系数。该方法将复杂问题分解为多个单一问题，通过比较权重系数的大小从而确定决策方案[9]。

在本应用中利用层次分析法并非得到最终决策方案，而是将不同预警等级视为两两相互独立的判断斜坡失稳的影响因素，通过比较各因素的重要性，构建判断矩阵，并得到该矩阵的权向量，即为各预警等级对应于判断斜坡稳定性的权重。

图1 层次分析法模型构建图

1.1.1 递阶层次结构的构建

以判断滑坡发生的可能性为目标层，预警等级为准则层，根据预警等级确定判断滑坡即将发生的可能性，构建递阶层次结构。由于在此结构体的构建中，仅需确定各预警等级的权重系数，未设置具体解决方案，所以无需子准则层。

1.1.2 构造两两比较判断矩阵

在建立递阶层次结构以后，各层次之间的影响关系就被确定下来。

根据Santy等人提出的一致矩阵法，可以将不同的两个预警等级之间对于判断斜坡稳定性的重要程度分为9个标度，即1-9(见表1)，并构建判断矩A。

表1 1-9标度的含义

不同预警等级对于判断斜坡稳定性的重要程度进行逐级均匀递增，并将两两预警等级对于判断滑坡是否进入临滑阶段的重要性程度进行比较，按1-9的标度划分得到：

(R:B)=9;(R:Y)=6;(R:O)=3;

(O:B)=6;(O:Y)=3;

(Y:B)=3。

由此得到判断矩阵：

1.1.3 权重计算

对于一个一致的判断矩阵，它的每一列归一化后就是相应的权重向量。采用这n个列向量的算术平均值作为权重向量,有：

(1)

Wi——矩阵A的特征向量；

n——矩阵的阶数。

其计算步骤如下：

第一步：将A矩阵元素进行归一化处理；

第二步：将归一化后的元素矩阵进行列项相加；

第三步：将相加后的向量除以矩阵阶数n即得权重向量。

计算得到：

w=[w1,w2,w3,w4]T=

[0.0466,0.1052,0.2571,0.5912]T

其中w1,w2,w3,w4分别表示蓝色、黄色、橙色、红色预警级别相对应的判断滑坡进入临滑阶段的权重系数。

1.1.4 一致性检验

由于判断矩阵的各元素在确定标度值时难免受到人为因素的影响, 因此在利用判断矩阵前需要对矩阵的优劣进行检验。具体检验步骤如下：

1.计算一致性指标C.I.

(2)

λmax——矩阵A的最大特征值；

n——矩阵A的阶数。

2.查找相应的平均随机一致性指标R.I(见表2)

表2 平均随机一致性指标R.I

计算一致性比例C.R.

(3)

根据Saaty教授给出的对判断矩阵一致性检验的一条准则，当C.R.<0.1时，认为判断矩阵的一致性是可以接受的[10]。

经一致性检验：

满足一致性要求。

1.2 监测点位置权重计算

同一后缘裂缝上，各监测点位移变化速率基本一致，在没有特殊外界条件的干扰下，监测曲线不会发生激增或陡降的变化。由于本文主要考虑在正常监测条件下，同一后缘裂缝上布设多个监测点位，根据各监测点不同预警等级，判断滑坡是否进入临滑阶段。因此忽略特殊因素对于监测过程的干扰，将各监测点位赋予相同的权重系数，监测点位越多,则各位置权重系数越小,即：

C=1/m

(4)

C——监测点位的权重；

m——监测点位的个数。

将监测点位置赋予相同的权重，使数据更均衡，可以尽量减小监测点位不同对判断斜坡稳定性带来的误差。

1.3 数据融合

根据现有滑坡监测系统所采用的四级预警指标，结合层次分析法计算的权重并引入主观概率[11]，得到判断斜坡稳定性的概率指标。根据四级预警等级的判定知，该等级仅与斜坡累计位移切线角度有关，且随着切线角度的增加，预警级别逐级提升，因此将预警等级权重系数进行逐个叠加，叠加后的结果视为根据预警等级判断滑坡是否进入临滑阶段的主观概率：

pB=0.05;

pY=0.05+0.10=0.15;

pO=005+0.10+0.26=0.41;

pR=0.05+0.10+0.26+0.59=1。

其中pB、pY、pO、pR均大于等于零且小于等于1，符合主观概率的定义，因此可将其视为由预警等级判断斜坡失稳的主观概率[12]。

将此主观概率与各监测点位置权重系数结合得到基于各监测点预警等级判断滑坡是否处于临滑阶段的概率，即得公式：

P=C·(pB·m1+pY·m2+pO·m3+pR·m4)·100%

且

mB+mY+mO+mR=m

(5)

其中，mB、mY、mO、mR分别表示处于某一预警等级的设备数量。

其中P即为根据各监测点的预警等级经融合后判断斜坡是否进入临滑阶段的概率，当此概率大于或等于50%时，即可判定该斜坡已经处于临滑阶段，监测预警平台可以此为依据发布预警信息。

2 应用案例

2019年2月17日凌晨5点53分，贵州省黔西南州兴义市龙井村9组发生了一起深层顺层岩质滑坡，超过60万m3山体失稳破坏，直接威胁了滑坡下方400多人的安危。由于针对该滑坡滑坡实施了专业监测预警，通过智能化的监测设备在滑坡发生前准确发出了预警信息，并配合科学的应急处置，使滑坡灾害实现了人员零伤亡和财产零损失(见图1)。针对该滑坡实施了专业监测预警，通过智能化的监测设备在滑坡发生前准确发出了预警信息，配合科学的应急处置，使滑坡灾害实现了人员零伤亡和财产零损失。

图2 龙井村滑坡基本概况

根据现场应急监测方案，在同一后缘裂缝上共布设6台智能地表位移监测设备，其具体布设方案见图2。2019年1月29日现场监测设备安装调试完毕，并将监测数据成功返回至地质灾害监测预警系统[13]，其系统界面如图3。在该系统中，分别设置了滑坡位移变化量、变形速率、切线角变化率、速度增量、速度倒数[14]等一系列评价滑坡稳定性的重要性参考指标。

图3 预警系统界面

在滑坡尚未进入临滑阶段之前，该智能地表位移监测设备始终以30分钟一次的采样频率进行数据采集，当滑坡变形速率加剧时，设备自动进入加密采集阶段，以每分钟1次的采集频率进行快速采样，所采集的数据通过无线传输技术[15]，传输至预警系统，根据现场监测数据所绘制的滑坡位移-时间曲线如图4[16]。

图4中不难发现4号装置的监测数据明显与其他数据有明显的差异，这是由于在2019年2月11日凌晨，由于坡体变形使该岩石沿张开的拉裂缝下坠，导致该位移计的监测数据明显激增，触发了红色等级，指示预警平台自动推送了错误预警信息。该预警信息一经发出后受到当地政府部门乃至省厅领导的重要关注，但经现场确认发现该斜坡整体依旧处于稳定状态，且仅4号监测点达到了红色危险等级，而其他监测点的危险等级仅为蓝色。造成这次误报的根本原因是因为监测预警系统未对各点位监测数据进行融合，仅根据单个监测点的危险等级对斜坡的整体稳定性进行判定，有失合理性和科学性。

若采用本文所提出的算法根据各监测点的危险等级对斜坡失稳的判定进行量化处理即得概率P：

P=0.166×(0.05×4+0.15×0+0.41×0+1×1)·100%P=20.8%

可得到当4号监测点的危险等级达到红色时判断斜坡整体是否进入临滑阶段的概率P仅为20.8%，远远小于50%，可以有效的避免类似误报的事情发生。

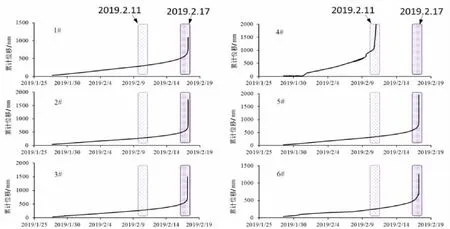
图4 各点位监测曲线

由于此次事件造成4号监测设备被破坏，在后续检测中仅有5台设备完成监测工作。2月17日凌晨5点09分第5号监测点首先达到红色预警等级并触发预警平台发布预警信息，此时其他4台监测的预警等级均已达到橙色，采用本文所提出的融合算法可以得到P=53%，可以确认该滑坡已经处于临滑阶段，可以发布预警信息，果然在凌晨5点53分发生滑坡，成功提前约50分钟实现临滑预警。

根据上述应用案例，本文提出的基于各监测点预警等级判定稳定性的数据融合方法，可以准确的识别错误信息并进行过滤处理，大大降低了预警信息误报的可能性，提高了监测预警系统识别滑坡进入临滑阶段的正确性。