基于数量化理论Ⅲ的地铁深基坑变形影响因素分析

(陕西铁路工程职业技术学院 基建处，陕西 渭南 714099)

1 研究背景

随着我国市政工程的快速发展，地铁基坑的数量也在日益增加，对其研究具有重要意义。在基坑开挖过程中，受土体卸荷的影响，基坑支护结构及周边地层均会出现不同程度的变形，若施工不当，可能进一步引发工程问题，造成不必要的损失。因此，基坑施工过程中的变形控制就显得格外重要，但基坑变形受多种因素的影响，如何确定各因素的影响程度，是采取相应控制措施的关键。

目前，有学者也开展了基坑变形影响因素的研究，如路明鉴[1]以有限元模拟为基础，分析了不同影响因素在基坑变形中的敏感性，有效判断了不同因素的影响程度；于洋等[2]利用FLAC3D模拟了基坑的开挖过程，确定了不同施工参数对基坑变形的影响效果，有效指导了现场设计及施工；张治国等[3]通过二维模拟，研究了基坑施工过程的支护参数及其位置对近接建筑物的影响，为类似工程施工积累经验；邢民等[4]重点分析了地铁基坑采用明挖法施工的变形影响因素，并提出了相应的施工控制措施。上述研究虽取得了一定的成果，但多偏向于数值模拟，也缺少数量化理论Ⅲ的应用研究，且不同地区的基坑变形影响因素具有差异，仍有必要对基坑变形影响因素进行针对性研究，所以，本文利用数量化理论Ⅲ进一步分析基坑变形的影响因素。数量化理论Ⅲ[5]能客观评价各因素间的影响程度，且能考虑各因素间的相互作用，虽在基坑工程中的应用较少，但在其他岩土领域已被广泛应用，如李军霞等[6]利用该理论分析不同影响因素对滑坡发育的影响程度，对滑坡防治提供了一定依据。

为验证数量化理论Ⅲ分析结果的准确性，鉴于BP神经网络在基坑变形预测中的适用性和有效性[7-10]，本文进一步以数量化理论Ⅲ的分析结果为基础，构建基坑变形预测的BP神经网络模型。通过资料收集，本文以30个基坑工程为实例背景，利用数量化理论Ⅲ分析不同影响因素对基坑变形的影响程度，确定出控制基坑变形的主导因素，再利用不同条件下的样品得分来评价各影响因素间的耦合程度；其次，根据数量化理论Ⅲ的分析结果，构建不同输入层条件的BP神经网络模型，实现基坑的变形预测，并利用预测精度来验证前期分析结果的准确性。

2 基本原理

2.1 数量化理论Ⅲ

数量化理论Ⅲ可得出对评价对象起主导作用的因素，进而实现评价对象的定量分类。在基坑工程中的应用过程为：首先，基于基坑变形影响因素统计，对不同影响因素进行区间划分，并构建反应矩阵；其次，根据计算确定各影响因素或其对应区间的得分值，进而判断各因素的影响程度；最后，以各影响因素的得分为基础，计算分析对象的得分值，且得分值的大小代表着各分析对象的危险性。同时，鉴于数量化理论Ⅲ的基本原理已在文献[6]中进行了详述，本文不再赘述。

根据数量化理论Ⅲ的原理，特征值不具唯一性，且特征值个数与类目个数相同，但特征值的大小与其可信度相关，即特征值越大，对应的特征向量具有更高的可信度。为实现各因素影响程度的综合评价，本文提出以最大3个特征值对应的特征向量作为各类目的得分向量。

其中，在各类目的影响程度评价中，将3个特征向量投影到空间坐标轴中，各类目即为空间坐标中的一个点，并以其空间距离l为评价指标，判断各类目的影响程度；在各项目的影响程度评价中，鉴于3个特征向量的可信度差异，以3个特征值为基础，对三者进行归一化处理，归一化值即为对应特征向量的组合权值，进而可得各类目的综合特征向量，以判断各项目的影响程度。

2.2 BP神经网络

BP神经网络是一种3层前馈神经网络，具有2个阶段学习过程，即正向学习过程和反向学习过程。同时，BP神经网络的基本原理已在相关文献[8,11]中进行了详述，本文也不再赘述。

结合实例特点，将BP神经网络构建为2种模型，即传统BP神经网络和优化BP神经网络，其中，传统BP神经网络的输入层为所有基坑变形影响因素，而优化BP神经网络的输入层为基坑变形的主导影响因素和重要影响因素，即后者的输入层剔除了一般影响因素。

3 实例分析

3.1 影响因素分析

基坑变形影响因素较多，具有较强的复杂性，结合工程实践及相关文献[12-13]的研究成果可知，基坑变形的影响因素主要可分为4类，分述如下。

(1)工程地质条件。该条件是地铁基坑变形的内在因素，其作用过程为：当工程地质条件较差时，会增加支护结构所受的土压力，进而导致基坑结构及周围地层出现变形。同时，影响土压力的主要土体参数包括土体重度、黏聚力及内摩擦角，其中，天然重度与土压力呈正比关系；抗剪强度指标与土压力呈反比关系。

(2)水文地质条件。在基坑开挖过程中，一般通过人工降水来保证施工条件，当地下水位降低时，会一定程度上增加土体的抗剪强度，进而减小支护结构所受的土压力、降低支护结构及周围地层的变形；反之，支护结构所受的土压力会增加，进而增加支护结构及周围地层的变形量。同时，在一定地层条件下，地下水位的变化会诱发管涌、流土等工程问题，且该问题与土体的渗透系数密切相关。因此，影响基坑变形的水文地质条件因素包含地下水位及渗透系数。

(3)基坑空间条件。基坑的空间条件指的是基坑的空间尺寸，包括基坑长度、宽度及深度。在相同条件下，基坑的空间尺寸越大，其支护结构及周围地层的变形量也越大；反之，基坑支护结构及周围地层的变形量越小。

(4)支护结构条件。为保证基坑稳定，支护结构是其施工过程中的必要手段，结合工程实例，影响基坑变形的支护结构参数主要包括支护结构刚度、嵌固深度及支撑间距等。

本文共收集30个工程实例[14-16]，结合前述基坑变形影响因素分析及各实例相关参数的区间分布，对各影响因素进行了类目划分，详见表1。由表1可知，基坑变形影响因素共计有11个，类目共计有33个。

表1 基坑变形影响因素及类目划分统计Table 1 Factors affecting the deformation of foundation pit and classification statistics

3.2 影响因素筛选

根据数量化理论Ⅲ的基本原理，通过构造反应矩阵来求解特征值及特征向量，且通过计算得到最大的3个特征值为：λ1=0.087 1,λ2=0.073 9，λ3=0.068 3。同时，对3个特征值进行归一化处理，得到对应3个特征向量的组合权值分别为：0.379 9,0.322 3，0.297 9。通过计算，得到3个特征值对应的向量(t1,t2,t3)得分及组合向量得分如表2所示。

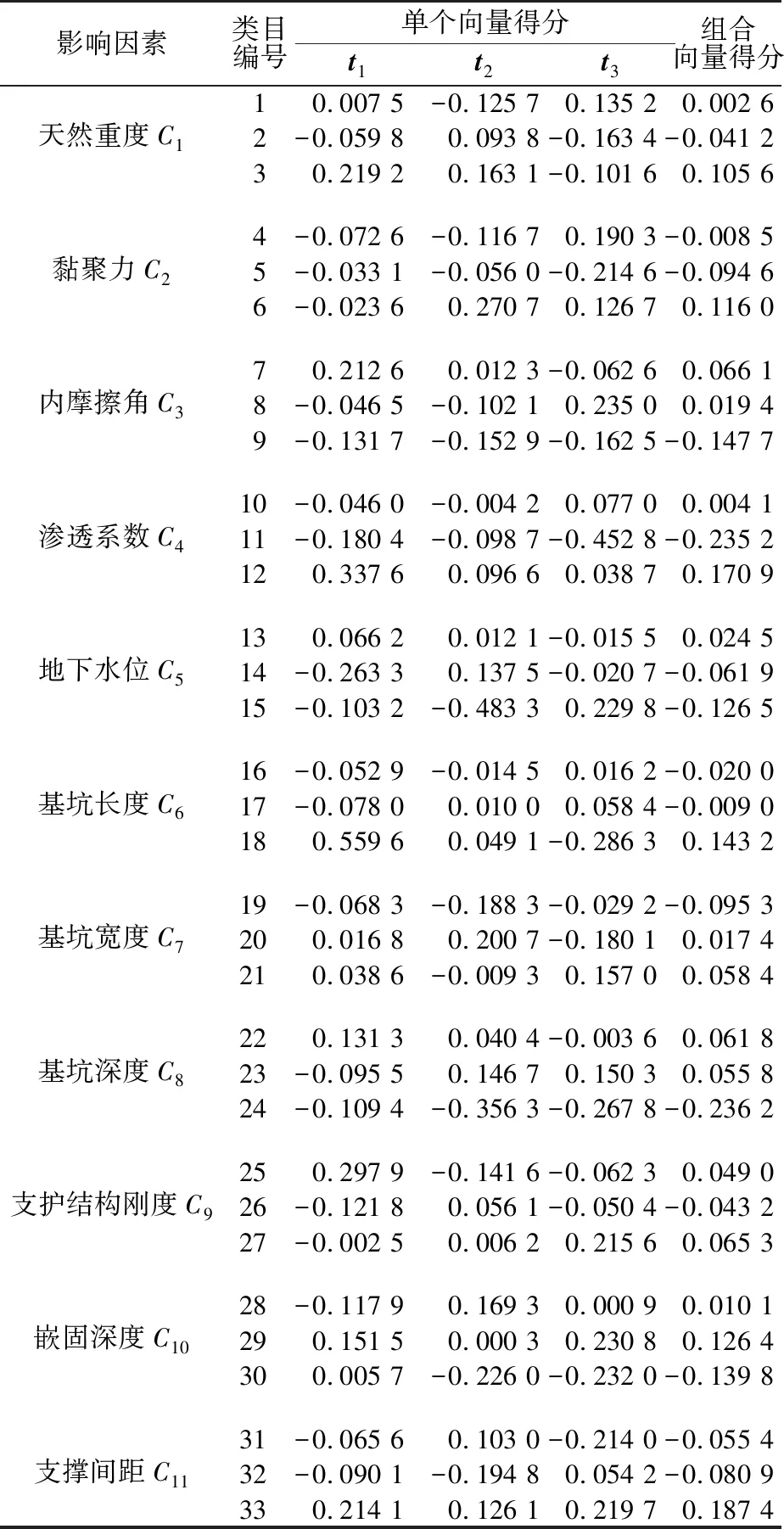
表2 类目向量及组合向量得分Table 2 Vectors of each class score and combinatorial score

3.2.1 类目影响程度筛分

以空间距离l为评价指标，筛分各类目的影响程度，且将各类目划分为3种类型：一般因素(l<0.15)、重要因素(0.15≤l≤0.3)和显著因素(l>0.3)。通过统计筛分，得各类目的影响程度划分如表3所示。由表3可知，显著因素的类目编号有6，11，12，15，18，24，25，30，33共计9个，占类目总数的27.27%；一般因素的类目编号有10，13，16，17，22，26共计6个，占类目总数的18.18%；其余均为重要因素，共计18个，占类目总数的54.55%。对比3类影响因素的分布情况可知，在基坑变形的类目影响因素中，以重要因素所占的比例最大，一般影响因素所占的比例最小。

表3 各类目影响程度筛分结果Table 3 Screening results of the degree of influence

3.2.2 项目影响程度筛分

以得分范围R和方差比η为评价指标，筛分各项目的影响程度，且也将项目划分为3类，即主导因素(R>0.25且η>0.018)、重要因素(0.15≤R≤0.25且0.006≤η≤0.018)和一般因素(R<0.15且η<0.06)。通过统计筛分，得各项目的影响程度划分如表4所示。由表4可知，主导因素包括渗透系数、基坑深度、支撑间距和嵌固深度，共计有4个，占项目总数的36.36%；重要因素包括内摩擦角、黏聚力、基坑长度、基坑宽度和地下水位，共计有4个，占项目总数的45.46%；天然重度及支护结构刚度为一般因素，占项目总数的18.18%。

3.3 耦合强度分析

根据前述，已对基坑变形影响因素进行了筛选划分，但基坑变形并非单一因素作用的结果，是多个因素共同作用的结果，因此，有必要进一步分析基坑

表4 各项目影响程度筛分结果Table 4 Screening results of the impact degree of each factor

变形影响因素间的耦合强度。耦合强度的分析过程为：①根据上述各类目得分，计算各样本得分，即包含一般影响因素条件下的样本得分；②剔除基坑变形的一般影响因素后，再计算各类目得分及样本得分，即剔除一般影响因素条件下的样本得分。以剔除一般影响因素前后的绝对样品得分差值s为评价指标，判断各影响因素间的耦合程度，且将耦合程度划分为3个区间，即高耦合度(|s|>0.030)、中耦合度(0.015≤|s|≤0.030)和低耦合度(|s|<0.015)。根据计算统计，得各因素的耦合度如表5所示。

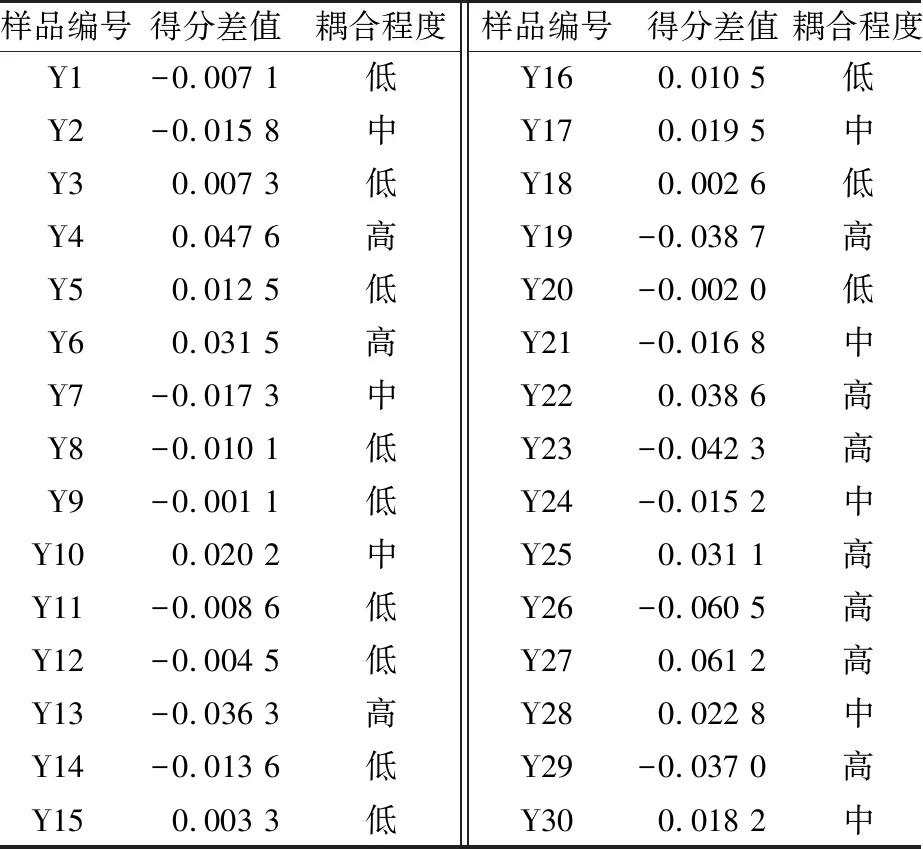
表5 影响因素的耦合度评价Table 5 Evaluation result of the coupling degree among influencing factors

由表5可知，30个样本的耦合程度各有差异，其中：Y4，Y6，Y13，Y19，Y22，Y23，Y25，Y26，Y27，Y29号样本属高耦合度，共计10个，占样本总数的33.33%；Y2，Y7，Y10，Y17，Y21，Y24，Y28，Y30号样本属中耦合度，共计8个，占样本总数的26.67%；其余样本为低耦合度，共计12个，占样本总数的40%。对比不同耦合度的分布区间可知，影响因素存在一定的耦合度，且中、低耦合度样本占比为66.67%，属主要耦合趋势。

3.4 可靠性验证

为验证前述影响因素筛分的有效性和准确性，以BP神经网络为基础，构建了2类预测模型，即传统BP神经网络，其输入层为所有基坑变形影响因素，对应变形量为输出层；优化BP神经网络，其输入层为基坑变形的主导影响因素和重要影响因素，也将对应变形量作为输出层。同时，以Y1—Y25号实例为训练样本，Y26—Y30号实例为验证样本，得2类模型的预测结果如表6所示。

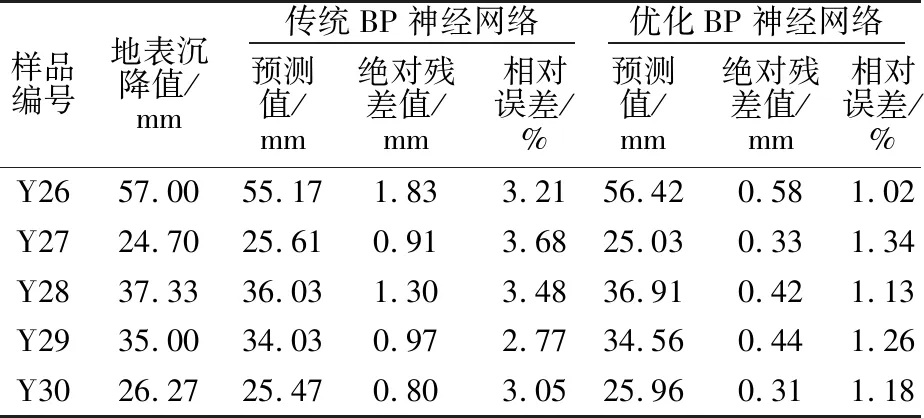
表6 2类模型的预测结果Table 6 Prediction results of the traditional and optimized BP neural network models

由表6可知，传统BP神经网络的最大、最小相对误差分别为3.68%和2.77%，平均相对误差为3.24%；优化BP神经网络的最大、最小相对误差分别为1.34%和1.02%，平均相对误差为1.18%。后者的预测精度明显优于前者，验证了前文影响因素筛选的准确性。

4 结 论

根据数量化理论Ⅲ及BP神经网络在基坑变形影响因素中的筛选和预测研究，主要得出了如下结论：

(1)根据数量化理论Ⅲ对基坑变形影响因素的筛选，得出渗透系数、基坑深度、支撑间距和嵌固深度是基坑变形的主导因素；土体内摩擦角、黏聚力、基坑长度、基坑宽度和地下水位是基坑变形的重要因素；天然重度及支护结构刚度为一般因素。

(2)通过剔除一般影响因素前后的绝对样品得分差值来评价各影响因素间的耦合程度，得出30个样本的耦合程度各有差异，其中，高耦合度样本共计10个，中耦合度样本共计8个，低耦合度样本共计12个，说明基坑变形影响因素间存在一定的耦合度，且中、低耦合度样本占比为66.67%，属主要耦合趋势。

(3)优化BP神经网络较传统BP神经网络具有相对更高的预测精度，验证了数量化理论Ⅲ对基坑变形影响因素筛选的准确性，为基坑变形的针对性控制提供了一定的参考。