“规范化考试”反向趋动作用的实证分析

2019-11-12熊方军张飞翔

中小企业管理与科技 2019年30期

熊方军，张飞翔

（广西财经学院，南宁530000）

1 引言

高校由“精英化”教育向“大众化”教育转型的过程中，高等教育质量问题成为社会各界共同关注的核心议题。教育部于2018年9月提出的《关于加快建设高水平教育，全面提高人才培养能力的意见》中明确指出本科教育是提高高等教育质量的最重要基础。陈宝生部长指出，目前我国高校要把“水课”变成有深度、有难度、有挑战度的“金课”。“金课”不仅包括教学前的准备与教学过程，也包括对教学结果的考核。造成高校教学质量差的原因是多方面的，譬如学生没有学习的积极性，老师没有好的教学方法，教学环境不佳等。哲学上讲“外因是通过内因才能起作用”，所以高校教学质量差的主要原因还是学生没有积极性。当前，高校教学过程中，单纯的思想教育对提高教学质量的作用并不明显。因此，高校应当严格开展考试工作，特别是要从考试前的复习、试卷的出题、监考、批卷这四个环节对高校考试进行规范化，真正做到“考前不泄题，试卷覆盖面较广、题型合理、难易程度适中，监考严格，考后批卷严格按标准执行”。

通过采取“规范化考试”能够反向趋动高校管理层、教师的责任心，也能够反向趋动高校学生的学习积极性与纪律性。但本文侧重点只在研究“规范化考试”对学生的反向趋动作用，即“规范化考试”反向趋动学生提高学习积极性与纪律性，并最终提高高校课程的教学质量。

2 文献回顾

现有的提高课程教学质量的研究文献中，主要集中在校园质量文化、教学模式与教学质量保障体系三个方面。

2.1 校园质量文化研究

关于校园质量文化的文献主要包括：姜雪（2012）在文章中谈到萨拉夫和塞巴思庭认为质量文化是一个机构在发展自己适应外部环境及处理内部事务能力的过程中所形成的关于质量价值的集体观念和认识；陈小丽（2015）以美国为例，认为“校园质量文化是集院校环境、观念、信仰、标准等多种因素为一体的”；张霆（2017）提出校园质量文化的建构应以新型高校管理文化、教师文化、育人文化及培植创新文化为主轴。

2.2 课程教学模式研究

关于课程教学模式的文献主要包括：马桂花（2018）对加拿大约克大学seminar 教学模式进行研究，认为这种模式我国可以借鉴；张乐，张云霞（2018）对“翻转课堂”模式进行了研究；曾令辉，石丽琴（2018）提出了“三三制”的教学模式；蒋金等（2018）提出，通过设立研究生助教岗位，推行以研究生助教参与辅助教学为基础的“大班授课-小班研讨”的“探研式——小班化”教学模式[1]。

2.3 课程教学质量保障体系研究

关于课程教学质量保障体系的文献主要包括：赵春鱼，吴华（2018）通过对摩尔根所提出的质量分析框架进行了修订，从设计质量、过程质量和结果质量三个层面构建高校内部质量保障体系；王中奎，胡啸天（2018）对英国高等教育的“卓越教学框架”进行介绍，认为英国高等教育的“卓越教学框架”值得我国借鉴[2]；杨秀平，张华，李亚兵（2018）提出，高校应从系统需求分析、系统的功能性需求、系统的功能组成构建高校教学质量评价系统。

从已有的相关研究可以看出，目前，我国有些高校校园质量文化比较缺失，有待进一步地培养和提高。教学模式基本上都是互联网与信息技术的组合。这些教学模式有共同目标，其任务是确保学生积极参与学习过程，与老师、其他学生互动，反思、决策和创新知识储备。但每种教学模式都有其自身的不足，都要满足特定的条件，只有当条件满足时才能达到好的教学效果。当前，课程质量保障体系越来越向“内生”性方面发展，通过不断改进，变得越来越复杂。课程质量保障体系通常涉及领域非常多，操作成本很高，不具备可操作性。

3 理论基础与研究假设

关于考试能够提高教学质量的相关文献主要包括：华德耀（2019）指出，考试是评价与测量教学质量的基本手段，不仅能够提高教学质量，而且能够促进教学改革和提高学校的办学水平[3]。杨涛（2017）认为，严格考试（“规范化考试”）不仅能够促进校园质量文化建设，而且还能够提高教学质量[4]。可以看出，学者们认为严格考试是可以提高教学质量的，但是通过“规范化考试”来提高教学质量，应该是“规范化考试”间接的作用，而不是直接的作用。因此，可以得出如下假设：

H1：实施“规范化考试”班级学生要比未实施“规范化考试”班级学生的学习积极性高；

H2：实施“规范化考试”班级学生要比未实施“规范化考试”班级学生的课堂纪律好；

H3：实施“规范化考试”班级学生要比未实施“规范化考试”班级学生的考试成绩好。

4 样本、数据、变量与模型

4.1 样本选择与数据来源

本文以广西财经学院开设了《会计学》这门课程的四个班（A、B、C、D）的224 名学生为样本。其中，A、C 两个班实施了“规范化考试”，B、D 两个班未实施“规范化考试”；A、B 两个班由一位教师授课，C、D 两个班由另外一位教师授课；A、B 两个班在教学过程所使用的教学资源、教学方法等都相同，C、D 两个班在教学过程所使用教学资源、教学方法等也都是相同的。

学习积极性与课堂纪律这两个定性指标数据来源于对这四个班学生的调查问卷，方法采用李克特五点分量表法，时间定于期末；学生考试成绩来源于这门课程的期中考试、期末模拟考试及期末考试的三次考试成绩（卷面分）的平均分。

4.2 变量定义

文章的因变量是一个虚拟变量（Y），表示“班级是否实施了‘规范化考试’”，如果实施了“规范化考试”，取值为1，否则为0；自变量有三个，分别用X1，X2 与X3 表示，其中，X1 表示“学习的积极性”，X2 表示“课程纪律”，X3 表示“考试成绩”，本文中用“考试成绩”来替代学生的“学习成绩”进行实证分析。变量具体定义如表1所示。

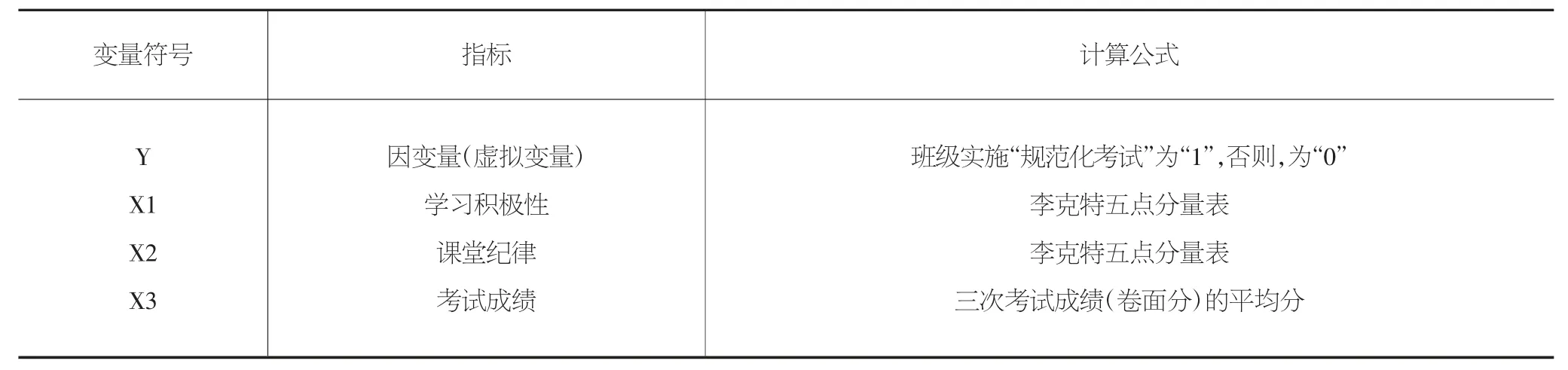
表1 变量定义

4.3 模型选择

本研究中的因变量是一个虚拟变量（Y），表示班级是否实施了“规范化考试”，实施了为1，否则为0。自变量有三个，分别是学习积极性、课堂纪律、《会计学》考试成绩。研究的目的是了解实施“规范化考试”班级是否比未实施“规范化考试”班级的学生的学习积极性、课堂纪律、学习成绩好。这符合模型的特点，所以文章以Y 为因变量，X1、X2、X3 为自变量，选择logistic 模型进行回归分析。

其回归模型如下：

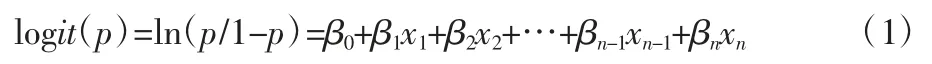
模型中的β0，β1，β2，…，βn-1，βn为自变量（X）的系数。

5 实证分析

5.1 回归分析（stata 12)

通过以Y 为因变量，X1、X2、X3 为自变量，利用logistic 模型进行回归分析，回归分析结果如表2所示。

表2 logistic 模型回归分析结果

从回归分析结果可以看出，回归分析后得到自变量X1 的P 值为0.001，自变量X2、X3 的P 值都为0；同时，得到自变量X1、X2、X3 的系数分别为2.97499、2.160155、1.031143，由此可以得出自变量X1、X2、X3 与因变量Y 之间存显著的正相关关系，由此假设H1、H2 和H3 都得到了证明。

5.2 方差膨胀因子分析（stata 12)

由于logistic 模型回归后不能进行方膨胀因子分析，所以文章在这里先进行普通多元回归分析，再进行方差膨胀因子分析，从方差膨胀因子分析结果可以看出，方差膨胀因子分析得到自变量X1、X2、X3 的方差膨胀因子分别是1.08、1.06、1.04，最大方差膨胀因子远远小于10，所以自变量X1、X2、X3之间不存在多重共线性的关系。

5.3 ROC 曲线分析（stata 12)

通过logistic 模型回归分析后，通过运用ROC 曲线的命令（lroc) 得出logistic 模型回归后ROC 曲线下的面积为0.8517。这意味着logistic 模型的判断正确率为85.17%，即1 判断为1、0 判断为0 的正确率为85.17%，这说明用logistic 模型进行回归分析是比较合理的。

5.4 描述性统计（stata 12)

自变量根据是否实施“规范化考试”分为实施“规范化考试”组和未实施“规范化考试”组，分别对两个组实施描述性统计分析，描述性统计分析结果显示X1、X2、X3 的平均值分别是3.637931、3.568966、60.63793 和 2.59253、2.703704、49.19444。这可以看出实施“规范化考试”班级组的学生学习积极性、课堂纪律、考试成绩这三个方面总体上要比没有实施“规范化考试”班级组的学生要好。

logistic 回归分析使得假设H1、H2、H3 都得到了证明；计算方差膨胀因子，证明了自变量X1、X2、X3 之间没有多重共线性的关系，说明用Y 作为因变量，X1、X2、X3 做自变量进行回归分析是合理的；计算ROC 曲线，证明了采用logistic 模型判断的正确率较高，也说明了采用logistic 模型进行回归分析是比较合理的；进行描述性统计分析，进一步佐证了假设H1、H2、H3 是成立的。