海洋深水井钻井过程中井筒温度的变化规律

李忠慧 赵 毅 楼一珊 李 中 方满宗 魏辰宇

1. 长江大学石油工程学院 2. 油气钻井技术国家工程实验室防漏堵漏研究室3. 中海石油（中国）有限公司湛江分公司 4. 国家电网北京市电力公司海淀供电公司

0 引言

较之于陆上及浅水钻井，深水钻井作业过程中既要面对高温高压作业的难点、又要面对深水作业的难点[1]。两者相互叠加形成上部超低温（3 ℃左右）和下部超高温（150 ℃左右）的温度差异，使得钻井液性能和地层岩石应力状态极不稳定，导致钻井液安全密度窗口变窄，极易造成井壁失稳，从而导致卡钻、泥包、钻具损毁等钻井事故，甚至使油井报废[2-3]。因此，准确的预测深水钻井过程中全井温度场变化对深水钻井作业的事故防范具有重要的意义。

研究表明，数学模型法是目前最准确、理论性最强的井筒温度场研究方法[4-5]。针对数学模型法，国内外学者进行了大量的研究。1962年，Ramey[6]根据井筒稳态传热假设，建立了井筒稳态传热模型[7]。Нasan等得出了不同地层条件下井筒温度的解析解[8-11]。稳态传热模型优于以地温梯度为基础的简易估算法，且其推导出的解析解使用方便，但由于换热过程是与时间相关的能量传递过程，稳态模型忽略了时间的影响，与实际情况不符。

1969年，Raymond[12]根据传热学及能量守恒等原理，建立了钻井液循环时井内温度场的控制方程，同时求解出控制方程的稳态结果和拟稳态结果。但是由于求解方法的限制，无法对温度场的动态变化进行研究。为了解决这一问题，Schoeppel和Bennett[13]提出，使用全隐式有限差分求解井筒温度场的瞬态数值解。在此基础上，国内外学者对其进行了补充与完善。一方面学者对控制模型中相关参数计算方法进行了补充：如对流传热系数[14-15]、海水强制对流和自然对流的努塞尔数求解方法[16]；另一方面学者对原始简单模型进行了补充：新增了黏性耗散热源项[17]、钻头处能量损耗[18]、钻柱旋转[19]、热源及强制对流换热[20]、海水对流换热和海域内隔水管[21]、钻井液物性参数变化[22]、环空岩屑[23]。随着研究的推进，对钻井液循环过程中的井筒温度场研究已逐步趋于完善，对温度场的求解精度也越来越高。但是，目前的研究假定只存在钻井液循环而忽略了钻进的影响，能量转换只局限于某一深度，而非一种动态变化。因此有必要考虑钻进过程对于深水循环温度场的影响。

笔者在钻井液循环温度场求解的基础上，采用节点更新法，研究在钻进过程中深水井筒温度场的变化趋势，分析不同机械钻速对井筒循环温度场的影响规律，以期为深水钻井过程中钻井液密度设计、井壁稳定性分析等相关工作提供更加准确可靠的依据。

1 钻井液循环过程中井筒温度场模型

1.1 模型依据

在钻井过程中钻井液在井筒内流动示意图如图1所示，图1显示了循环过程中地层、海水及井筒内各个部分之间的热量传递关系。循环过程在现有模型基础上[21]新增了节点更新区域（蓝色虚线框），该区域大小与变化规律与实际的机械钻速有关。

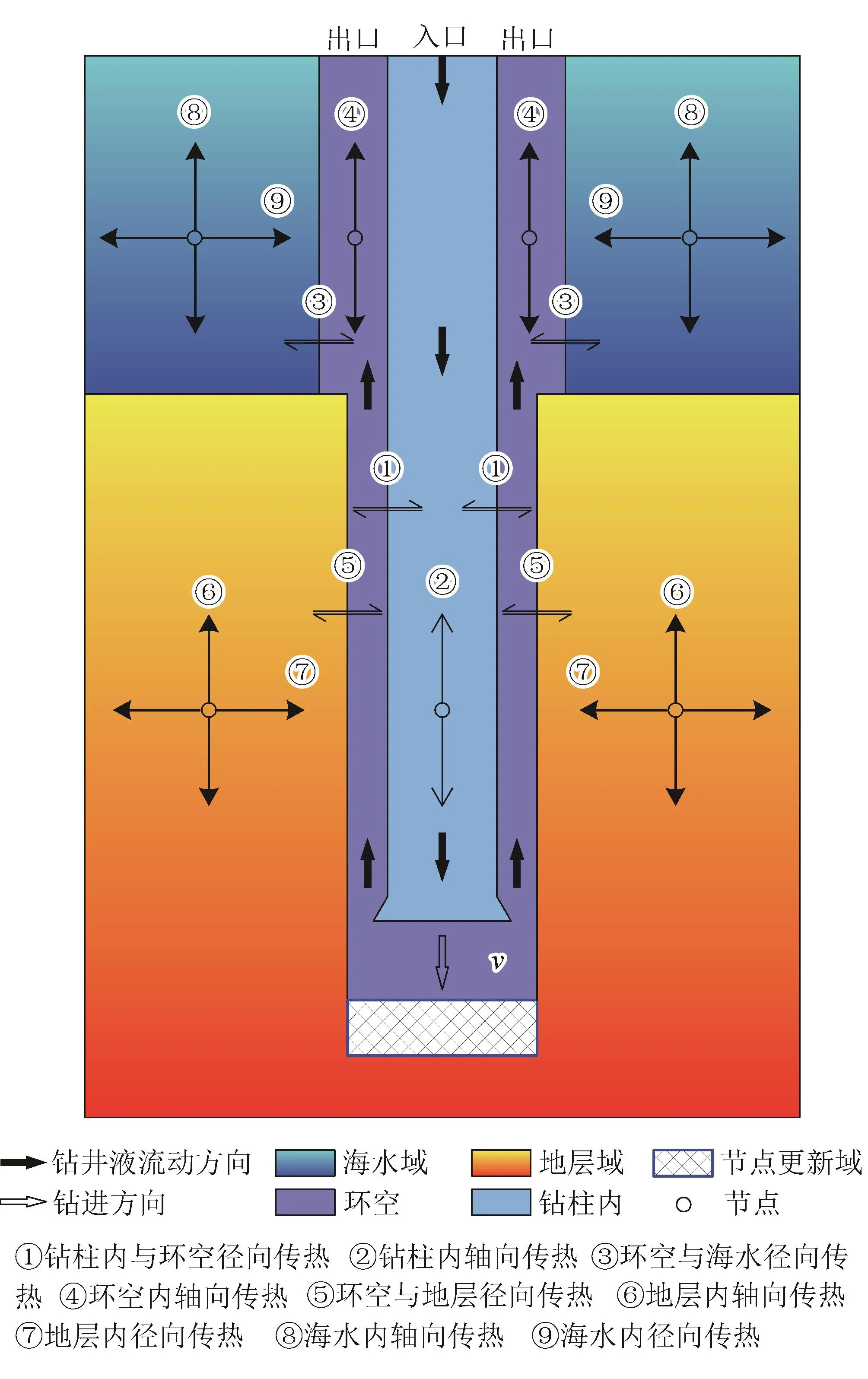
图1 深水钻井过程中井筒模型图

1.2 计算模型

1.2.1 模型假设

1）模型中各材料的热物性参数（如密度、比热容、导热系数等）始终为一常量，不随温度压力等因素变化。

2）对于管柱内和环空内的流体，只考虑液体轴向强制对流换热和径向对流换热及流动摩阻产生的能量损失。

3）考虑海水在管柱外的对流换热；地层中考虑垂直和水平方向的热传导。

4）忽略水泥石及套管的影响，认为整个井筒为裸眼井筒。

1.2.2 钻进过程中能量守恒方程

1.2.2.1 钻柱内控制体

1）轴向能量传递：轴向摩擦能量损失＋轴向热对流能量交换

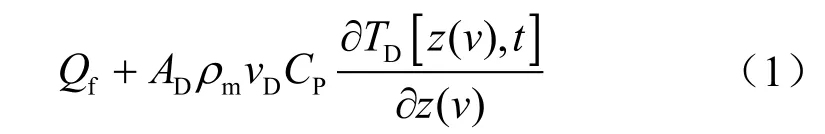
2）径向能量传递：环空热对流能量交换

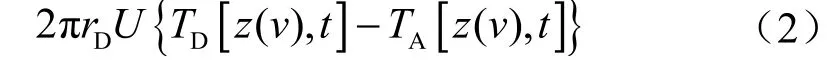
3）时间效应

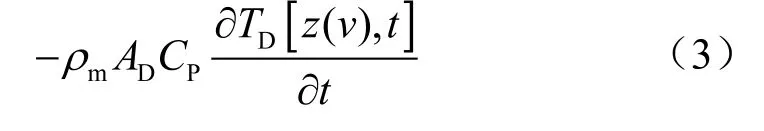
1.2.2.2 地层段环空内钻井液温度控制方程

1）轴向能量传递：轴向摩擦能量损失＋轴向热对流能量交换

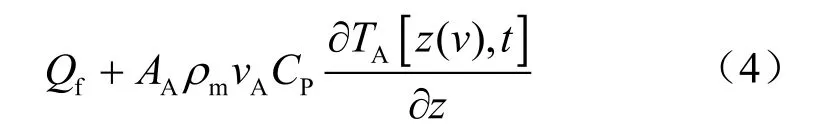
2）径向能量传递：钻柱内热对流能量交换＋井壁热对流交换

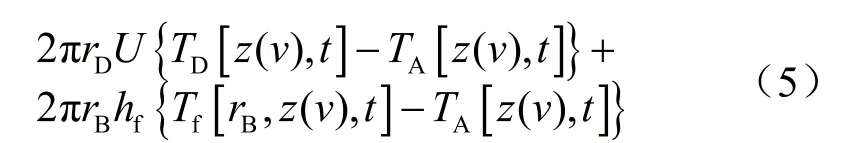
3）时间效应

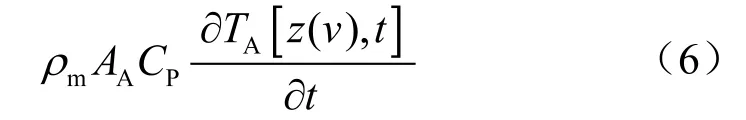
1.2.2.3 海水段环空内钻井液温度控制方程

1）轴向能量传递：轴向摩擦能量损失＋轴向热对流能量交换

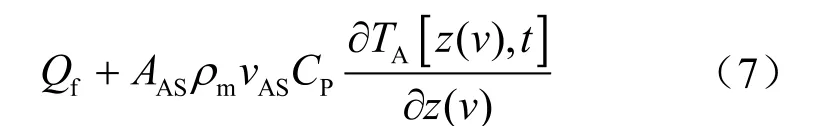
2）径向能量传递：钻柱内热对流能量交换＋井壁热对流交换

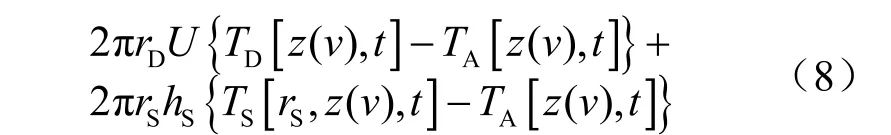
3）时间效应

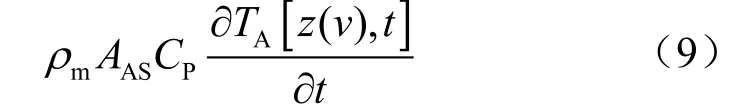
1.2.2.4 地层岩石温度控制方程

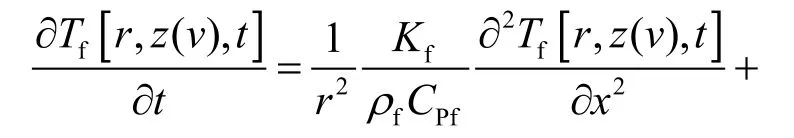
1.2.2.5 海水温度控制方程

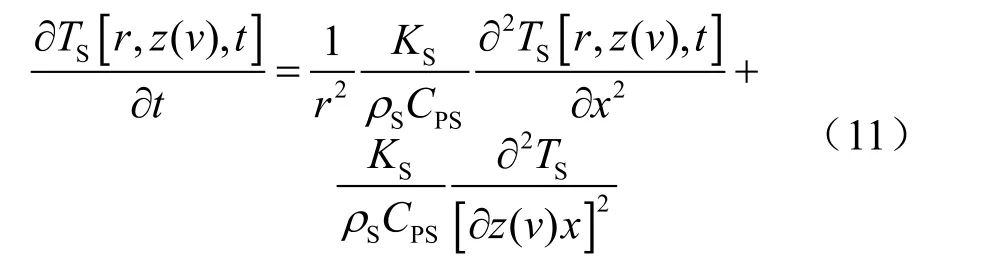
1.2.2.6 井壁温度控制方程

1.2.3 定解条件

问题边界条件及初始条件由以下方程描述：

1.2.3.1 边界条件

1）已知钻井液入口温度：

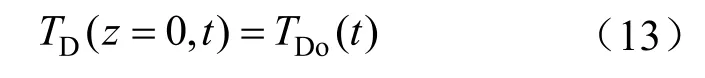
2）钻柱内流体和环空流体温度在井底处相等：

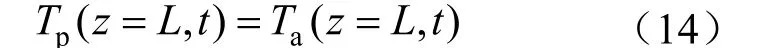
3）地层无穷远处地层温度为原始地层静止温度

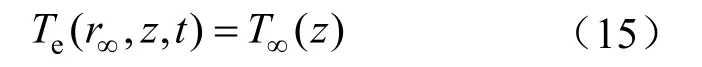
1.2.3.2 初始条件

1）海域内，钻柱内流体和环空流体的初始温度为初始海水温度，即

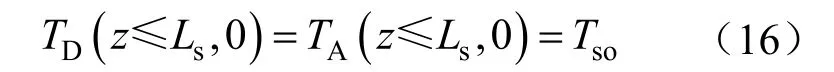
2）地层区域内，钻柱内流体和环空流体的温度为原始地层静止温度，即

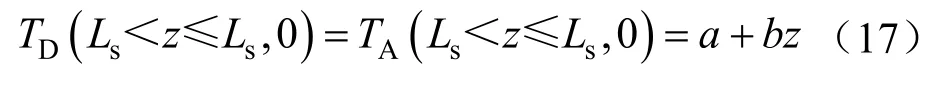
2 模型求解及模型验证

2.1 模型求解流程

通过有限差分和高斯赛尔德迭代法进行全井温度场的求取，求解思路如图2所示。①根据全井信息及计算要求划分时间节点及空间节点；②根据给出的初始条件为全井各节点处赋温度初值；③时间步进一步，新增井底节点，根据新划分节点及控制方程对各个节点对应的控制方程进行有限差分计算该时刻全井温度场分布；④时间继续步进，求取各个时间节点对应的全井温度场分布；⑤当时间节点步进至超过最终目标时间时，停止计算并输出目标时刻全井温度场分布曲线。

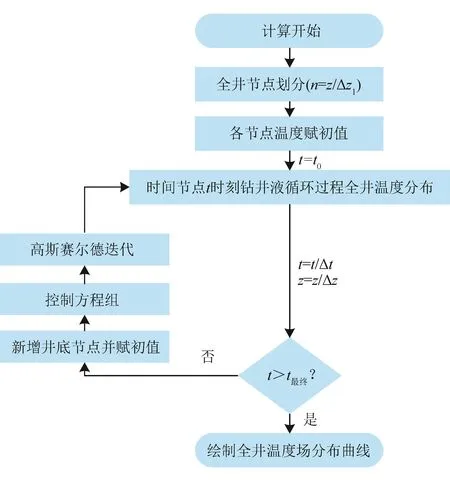
图2 钻进过程中全井温度场计算流程图

与现有计算方法相比[24-25]，本文在第三步使用迭代法求取全井温度场过程中，新增了节点更新这一步骤，相对现有研究，更符合现场实际。

2.2 实例验证

本文以文献[21]中数据为例，水深959 m，起始井深 2 770 m，平均机械钻速 16 m/h，钻进 9 h 至井深2 914 m。钻杆外径 149.2 mm、钻杆内径 127 mm、井眼尺寸 444.5 mm ；508 mm 隔水管内径为 469.9 mm ；海水表层温度为15 ℃，海水底层温度3 ℃，海水流速0.2 m/s，假设在200 m深度内线性降低到3 ℃，之后保持不变直到海底。循环排量4 550 L/min、增压流量 2 000 L/min、入口温度 22 ℃、地表温度 23.8 ℃、地温梯度0.036 1 ℃/m、钻井液n值0.55、钻井液k值1.02 Рa·sn，计算需要的其他材料热物理性能如表1所示。

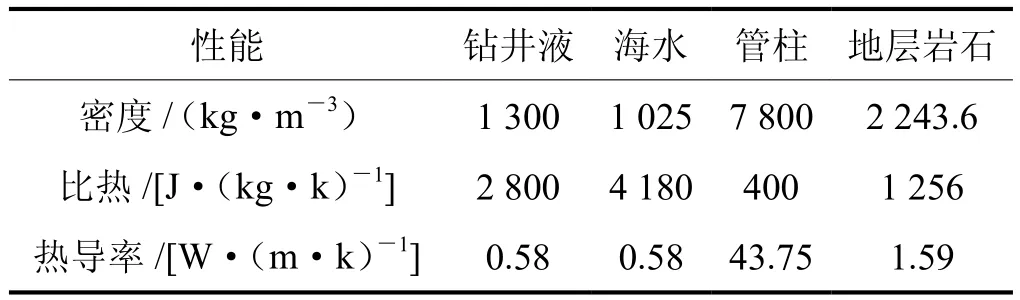
表1 计算所需热物理性能表

计算结果如图3所示。由图3可以看出，从2 770 m 开始钻进，以 16 m/h 的钻进速度钻至 2 914 m过程中井底随钻温度的变化情况。随着钻进深度的增加，实测井底随钻温度也逐渐增加，笔者计算结果与实测值趋势基本一致，二者最大误差为1.39%，符合工程计算误差的要求，即该方法可用于深水钻进过程中循环温度场的计算。

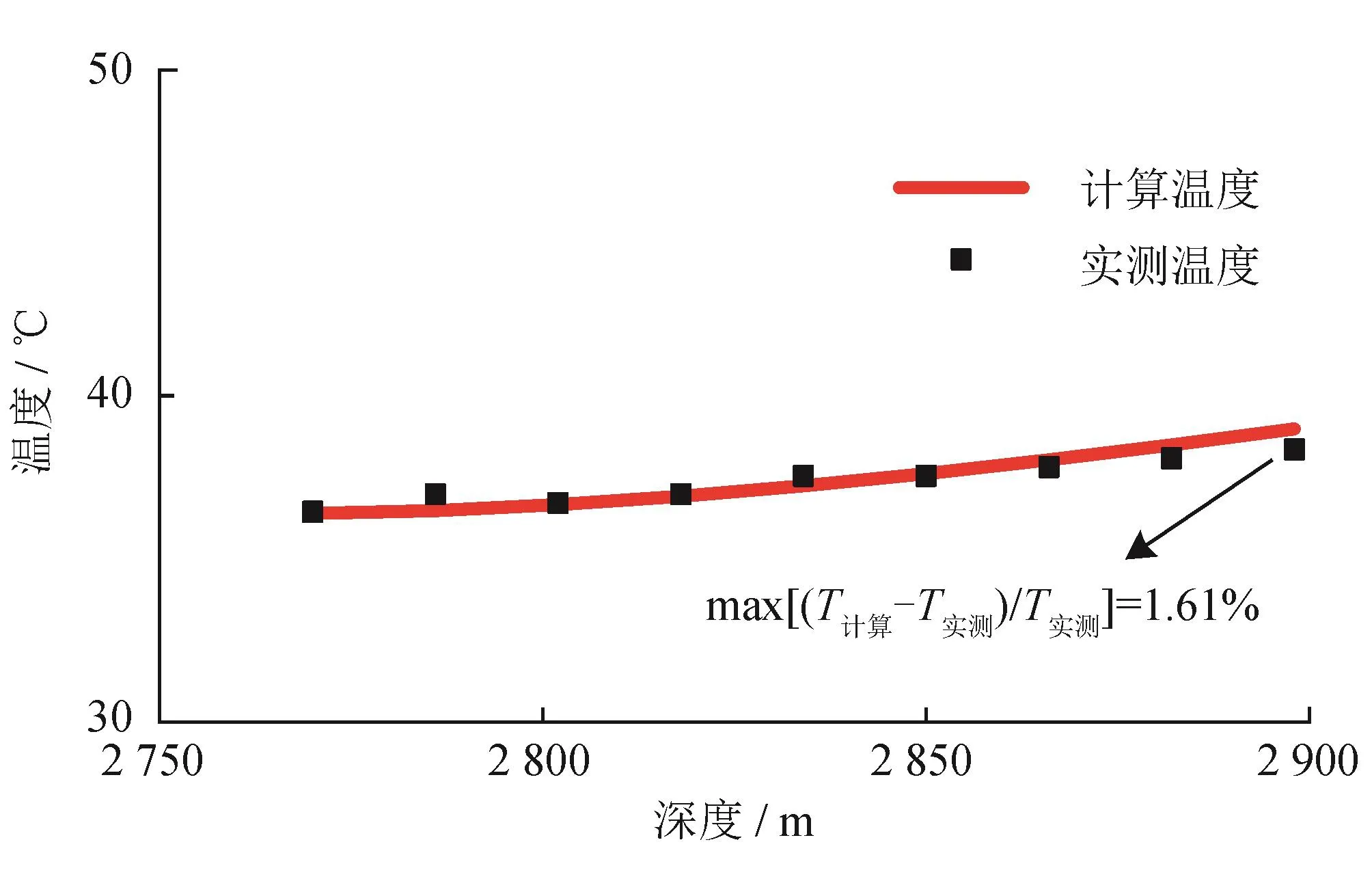
图3 实测与计算随钻温度结果对比图

3 案例分析

以南海深水某气井相关数据进行案例分析考虑不同机械钻速钻进至相同井深、不同机械钻速钻进相同时间，环空循环钻井液温度场的变化特征。采用海水作为钻井液随深度温度变化如式（18）所示，井眼相关参数及所需热力学属性如表2所示。计算结果如图4～7所示。

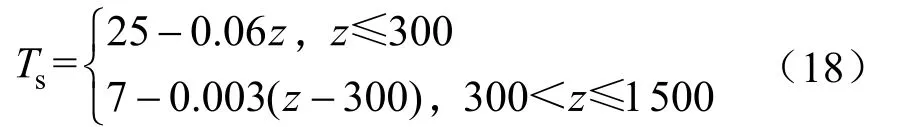
图4为相同深度下不同机械钻速对井筒温度的影响。当起始深度为3 000 m，随着钻进深度的加深，3 种机械钻速对应的环空出口温度均上升[9]，但是循环温度却一直保持Tv=5m/h＞Tv=10m/h＞Tv=20m/h的相对关系，且v=5 m/h时其出口温度增大速率也大于v=10 m/h和v=20 m/h情况下环空出口温度增大速率。出现这种情况的主要原因是：①受地温梯度的控制，在限定初值深度条件下，机械钻速越小，钻进至相同深度需要的时间越长，钻井液循环时间就越长（循环周次数越多），与地层进行的热交换越多，其带出的热量也就随之增大，则温度增加越快；②考察图4-b与图4-a，钻井进尺60 m，3种机械钻速条件下，需要钻进时间分别为 12 h、6 h、3 h，相当于钻井液分别循环了8、4、2周，钻井液从离开钻头水眼进入环空就向地层吸热，带着地层热量的钻井液向上循环必然转入向上部地层加热（钻井液散热），随着循环钻井液加热井壁时间增加，循环的钻井液保存更多的热量，因而钻井液出口温度逐渐升高。

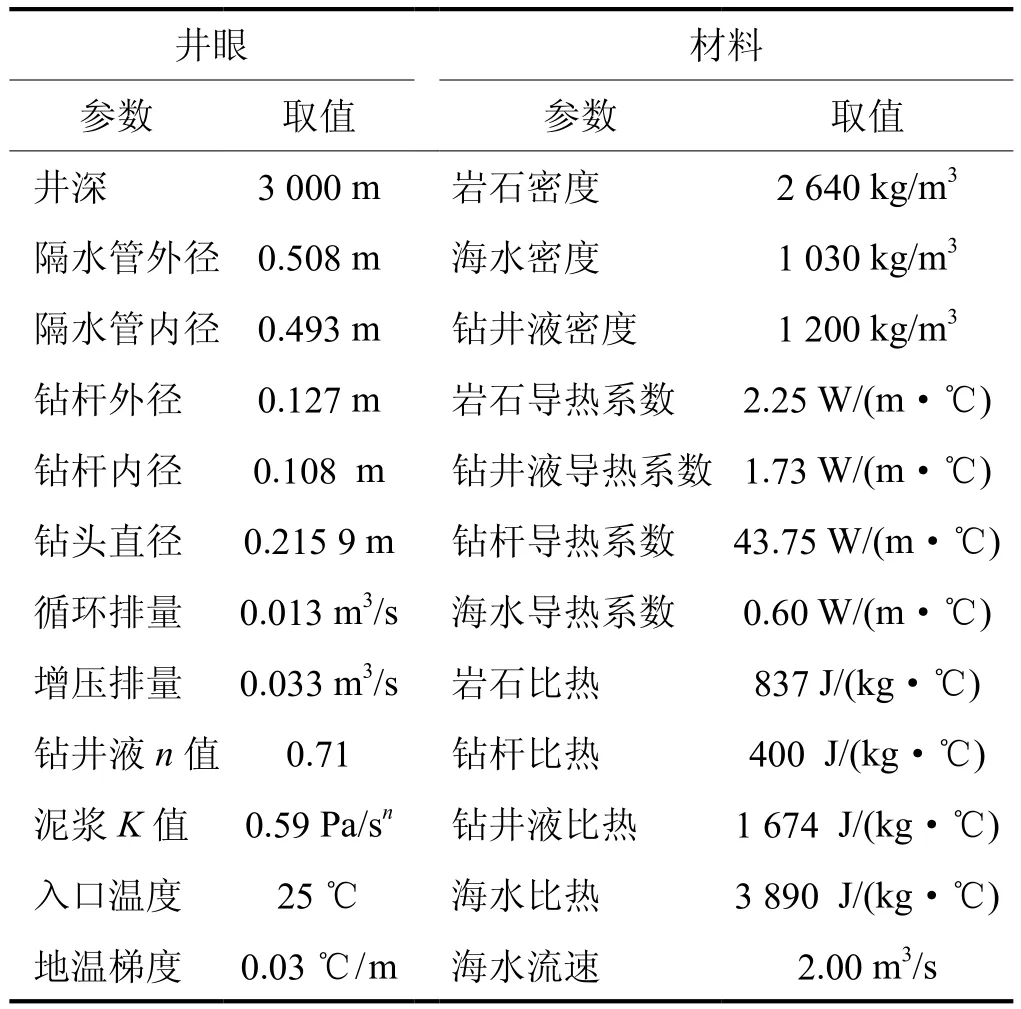
表2 井眼信息及计算所需热力学参数表

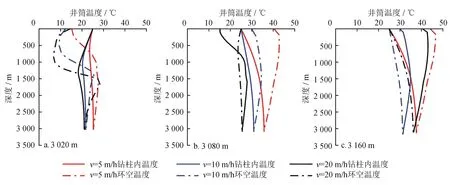
图4 相同深度下不同机械钻速对井筒温度的影响

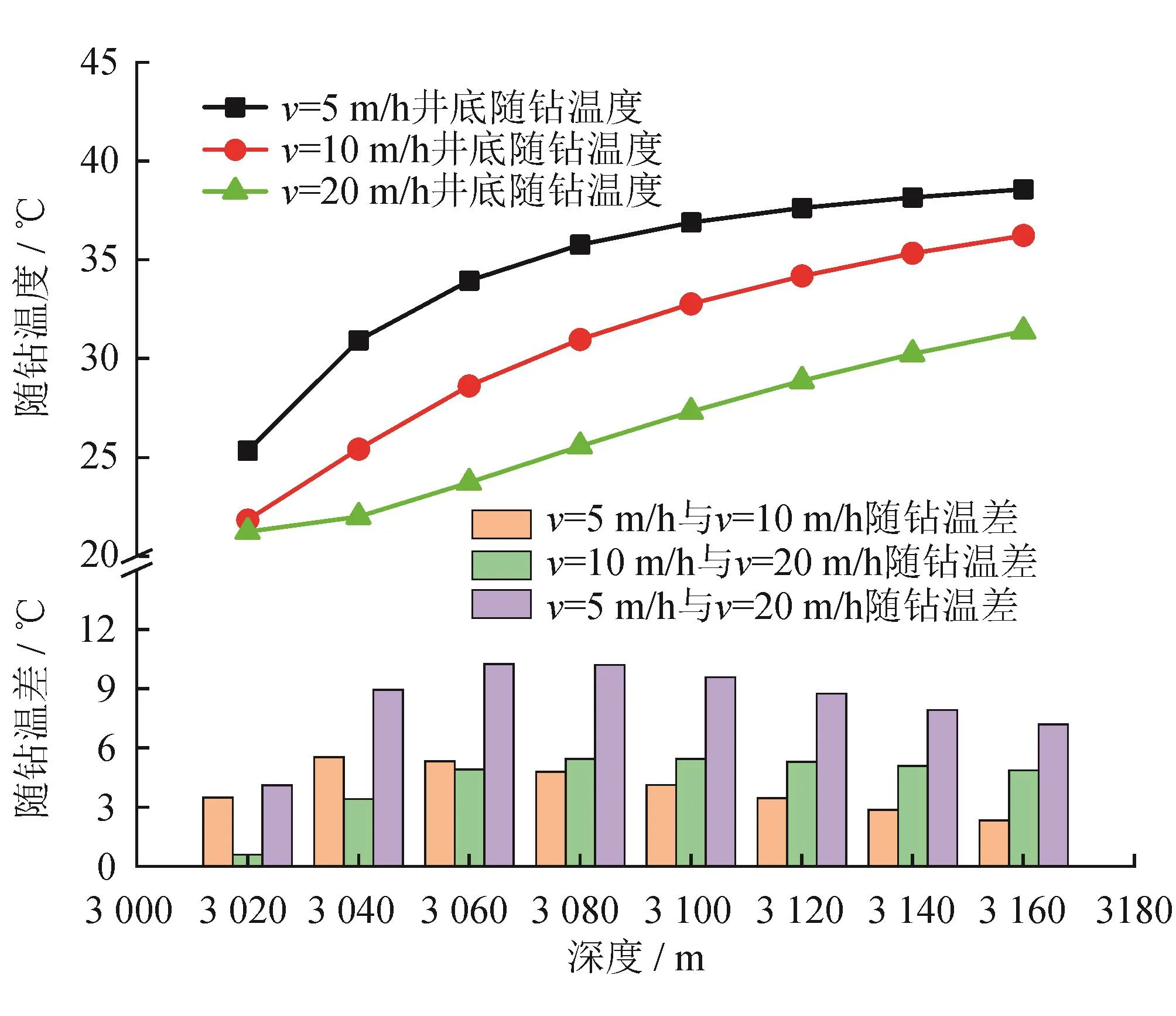
图5 相同深度下不同机械钻速对随钻温度的影响图

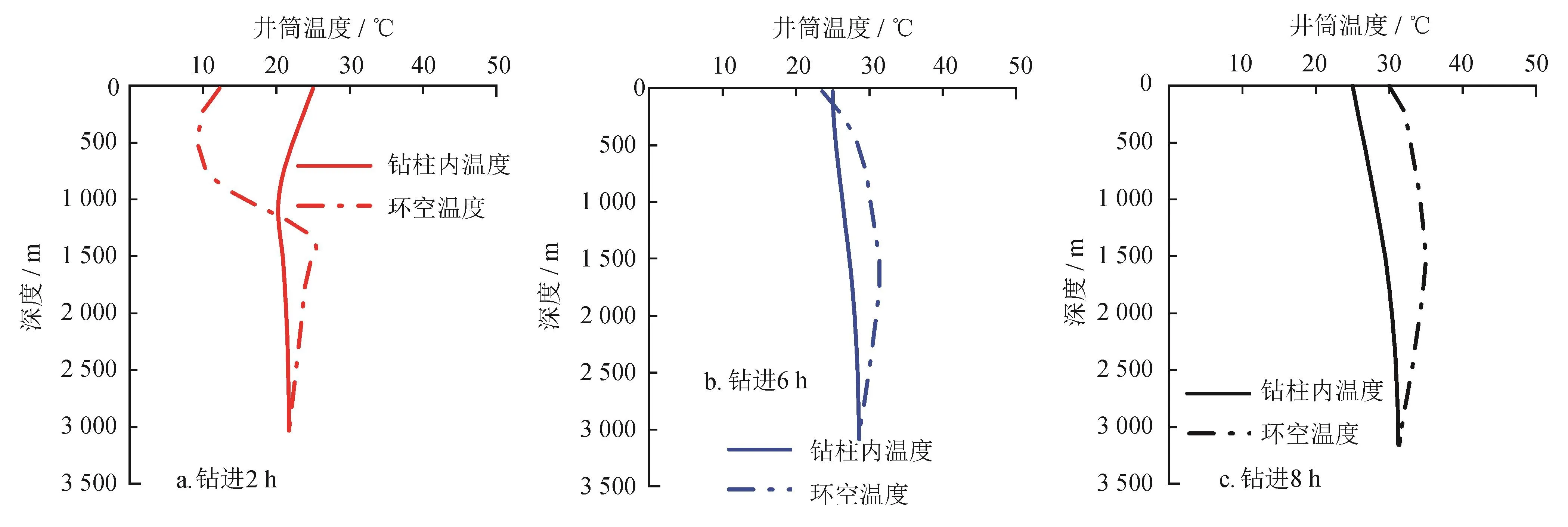
图6 相同钻进时间下3种机械钻速对井筒温度的影响图

为比较3种机械钻速条件下井底随钻温度差异，计算分析了不同深度条件下井底随钻温度变化，如图5所示。

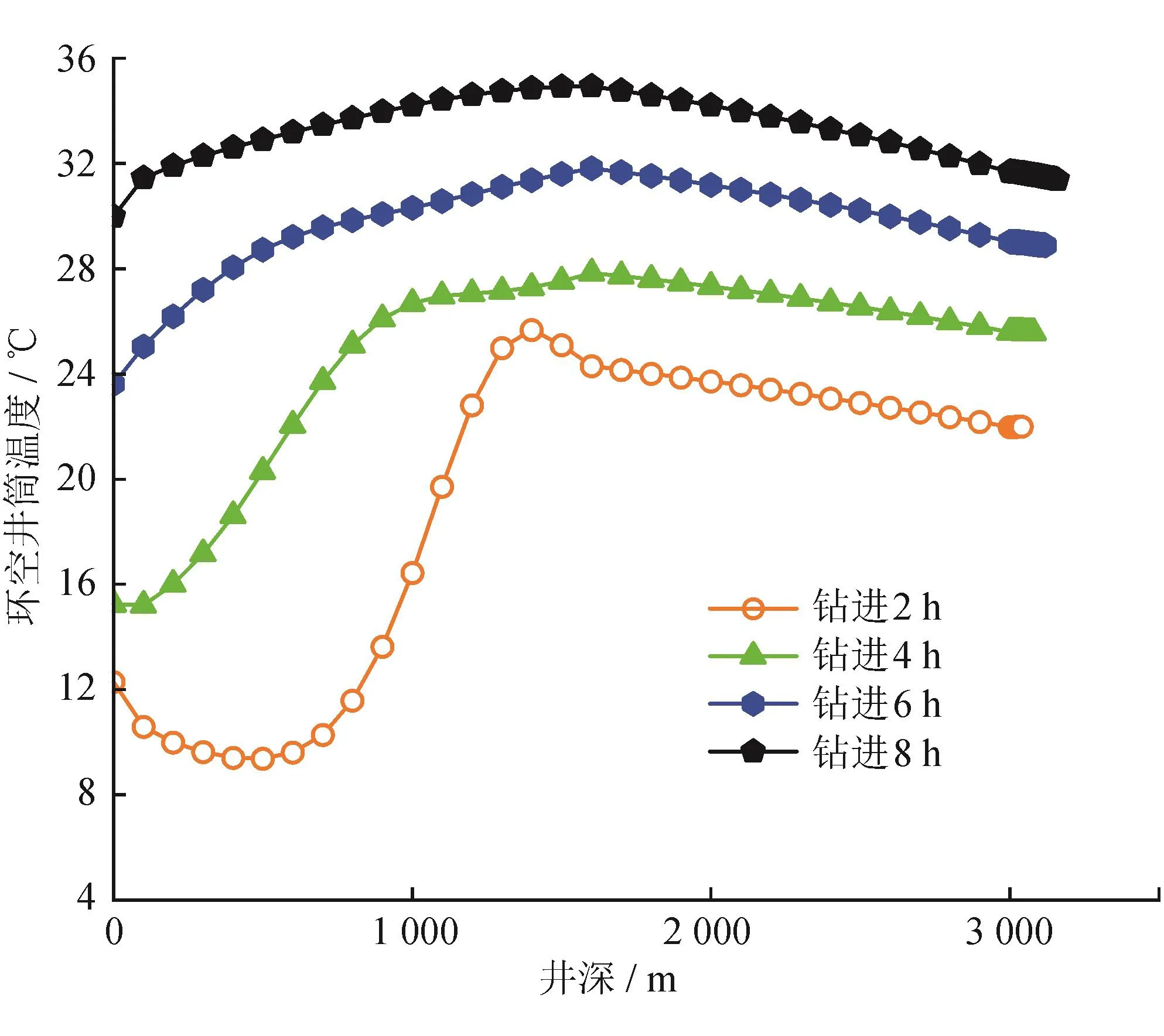
图7 20 m/h机械钻速下环空井筒温度随时间变化图

由图5可知，3种条件下井底随钻温度均随井深逐渐增大，与现场实际情况一致；而由于循环时间的差异，机械钻速越小的井底循环温度越大。对比不同机械钻速井底随钻温度差值直方图可知，井底随钻温度差值随机械钻速差异增大而增大，v=5 m/h和v=20 m/h的井底随钻温度差异最大，最大值接近10 ℃。任意两种机械钻速条件下，其井底随钻温度差值均随深度增加先增大后减小，其主要原因是随着循环时间的逐渐增大，井筒循环温度逐渐升高，但其存在温度上限（地层原始温度），导致井筒循环钻井液不会与地层无限制的热交换，而是最终趋于一种温度一致的稳定状态，差异减小正说明了循环温度场趋于稳态这一过程。

图6、7则表示的是在初始深度一定条件下，不同钻进时间对井筒循环温度场的影响。

由图6可知，对于相同钻进时间3种机械钻速条件下循环温度场差距在浅部地层和海水段，循环6 h在井口的温度已与入口钻井液温度一致，而循环8 h在井口的温度大于入口钻井液温度，中下部井段环空循环温度场的变化不大，这是因为按3种机械钻速钻进，6 h 可以分别从井深 3 000 m 钻至井深 3 030 m、3 060 m、3 120 m，地温增加值约 3 ℃，钻柱内外的3条温度曲线几乎是重合的。这一结果说明，在钻进过程中循环温度场对循环时间的敏感性要远高于对机械钻速的敏感性。

但是通过分析单一钻速条件下循环温度场随时间的变化规律（以v=20 m/h为例），如图7所示。虽然其井底随钻温度随着时间的增加而逐渐增大，与本文文献[20,26-27]一致。但却不具有文献中的温度分界点，而是呈现整体增大的趋势，这种差异主要来自于机械钻速的影响，随着钻进的进行，深度增大，井底地层温度就随之增大，导致井内温度整体增大，而不是出现上部减小下部增大的温度分界情况。

4 结论与建议

1）在同一深度全井循环温度场随机械钻速变化有明显变化，其井底随钻温度会随着机械钻速的变化出现明显差异，对于水深1 000 m钻井，差异最高可达10 ℃，对实际井筒循环温度场具有较大影响。

2）钻进循环温度场对时间的敏感性要远高于对于机械钻速的敏感性。与现有研究不同的是，由于井深的加深，钻遇地层温度的升高，导致钻进过程中循环温度场整体增大。

3）通过对随钻循环温度场的研究，可以研究井底随钻温度的变化情况，再根据热应力等条件进而可以分析井底复杂情况下的井壁稳定性等实际钻井复杂情况。

符 号 说 明

Qf表示摩擦压降导致的能量损失（钻头处包括钻头压力降），J；AD、AA、AAs分别表示钻柱内、地层环空、海水段环空横截面积，m2/s；vD、vA、vAs分别表示钻柱内、地层环空、海水段环空钻井液流速，m/s；v表示机械钻速，m/h；r、rB、rD分别表示距井眼中心的距离、井眼半径、钻柱半径，m；Cp、Cps、Cpf分别表示钻井液、海水、地层比热容，J/(kg·℃)；TD、TA、Tf、Ts分别表示钻柱内、环空、地层、海水的温度，℃；U表示综合对流换热系数，无量纲；ρm、ρf、ρs分别表示钻井液密度、地层密度、海水密度，kg/m3；Kf、Ks分别表示地层、海水导热系数，W/(m·℃)；z(v)=z(v)t-1+Δz表示控制单元长度，Δz=vΔt，m；t表示时间，s；TDo、Te、T∞(z)、Tso分别表示钻井液入口温度、地层内部温度、地层原始温度、海水原始温度，℃；a表示海底泥面温度，℃；b表示地层温度梯度，℃/m；L、Ls、z分别表示海水深度、井深、计算目标深度，m。