GPS高程拟合在既有轨道高程勘测中的应用研究
2019-11-12任洁韩峰
任洁,韩峰
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
0 引 言
近年来,国家经济建设持续稳步发展,运输需求快速上升,铁路运输承担的客、货运量越来越大, 实现既有铁路的快速高效勘测及养护已成为研究热点[1].受制于高程误差,实时动态(RTK)具有的高精度、全天候优势不能得以发挥[2],在既有线高程测量中仍广泛地使用效率较低的传统水准作业模式.如何将RTK技术与周边水准点的分布相结合,采用空间拟合算法实现其在既有线测量中的应用,具有重要意义.
由于RTK测量技术是以WGS-84椭球为参考面得到的大地高,而实践过程中,需要以似大地水准面为基准的正常高,因此需将高程进行转换[3].由于参考面不一样,不同测量技术获得的高程存在差异,所以高程异常的获取成为关键[4].重力是高程异常值的主要影响因素,但是地球质量分布不均,在不同地区、不同条件下重力场资料难以获得[5],基于重力的高程转换难以实现,因此国内外学者对如何把GPS获取的大地高转换为正常高进行了大量的研究.文献[6]研究了GPS高程拟合在道路工程测量中的应用,阐述了GPS技术在公路工程中应用的情况和特点.文献[7]通过GPS控制网的优化设计及高程异常拟合的应用研究,分析了控制网优化设计方法.文献[8]分析了GPS高程拟合模型精度.文献[9]根据GPS高程拟合在跨海桥梁中的应用方法,提出了基于二次多项式曲面的跨海桥梁工程GPS高程拟合方法.建立GPS高程拟合模型目前常用的有平面拟合模型以及二次曲面拟合模型,本文提出自动化二次曲面拟合方法,分析不同间隔控制点条件下优化模型的精度,并通过实际工程案例验证RTK测量代替传统水准测量的可行性.
1 高程拟合模型
RTK技术作为一种快速、高精度的测量手段,应用越来越广泛[10].但RTK技术获得的三维数据具有平面精度高、高程精度低的特点[11].因此在将RTK测量得到的GPS高程即大地高程转换为实际运用的水准高程即正常高的时候, 需要一种转换方法来提高转换后高程精度.本文提出了一种自动化二次曲面模型方法来进行转换分析[12].并通过实例分析自动化二次曲面拟合模型与自动化平面拟合模型的精度对比.大地高与正常高的关系可以表示为
ε=Hd-Hz,
(1)
式中:ε表示高程异常;Hd表示大地高程;Hz表示正常高程.
1.1 平面拟合模型
平面模型将研究区域内的高程异常看做是点坐标的平面函数[13].平面模型的数学表达式如下:
εi=a0+a1xi+a2yi,
(2)
式中:ai(i=0,1,2)为平面模型的参数;εi为高程异常;(xi,yi)为研究区域内已知点的坐标.平面模型对应的误差方程的矩阵形式如下:
V=AX-L.
(3)
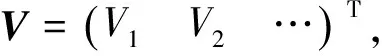
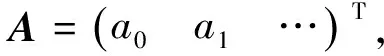

根据间接平差原理可得:

(4)
基于Matlab最小二乘原理进行编程,可快速解算出模型的参数.解算模型参数至少需要测区内3个控制点的GPS高程和水准高程.
1.2 二次曲面拟合模型
二次曲面模型将研究范围区域内的高程异常假设为1个复杂曲面[14].二次曲面模型的数学表达式为
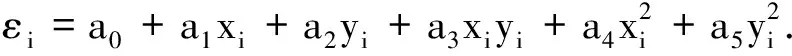
(5)
式中:ai(i=0,1,2,3,4,5)表示二次曲面模型的参数;εi表示高程异常;(xi,yi)表示研究区域内已知点的坐标.二次曲面模型对应的误差方程的矩阵形式为
V=BX-L,
(6)
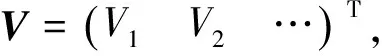
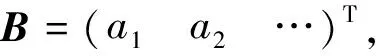
表示高程异常的矩阵.
利用最小二乘原理进行Matlab编程,可快速解算出二次曲面拟合模型所求参数,解算二次曲面拟合模型时至少需要6个控制点的GPS高程和水准高程.
1.3 自动选取结点
根据上文所述平面模型和二次曲面模型在进行拟合时,分别至少需要3个和6个控制点.但是实际中控制点个数较多时,需要合理地选取最少控制点,本文把自动选取出来的控制点称为结点.结点的选取对模型结果具有非常重要的影响,如何准确地选取结点使拟合后的模型达到最优,具有重要意义.本文针对这种现象,提出了一种自动选取不等间隔结点的模型,自动选取模型所需结点和结点个数,并利用最小二乘法计算出模型参数.
在进行自动选取结点时提出质量指标的概念,所谓的质量指标就是评定控制网设计好坏的标准.自动选取结点步骤如下:
1)假设测区内每个控制点都可看做一个结点,计算每个结点与相邻结点的距离.
2)计算每个结点与相邻结点间的质量指标Qi,并将质量指标小的删除.
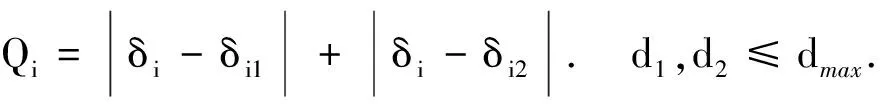
(7)
式中:δi表示第i个结点的高程异常,即GPS测得的大地高与水准仪测的正常高的差值;δi1,δi2表示与相邻结点的高程差;d1,d2表示与相邻结点的距离.
选取出质量指标最大的3或6个结点,即为平面拟合模型所需的3个或二次曲面模型所需的6个结点,计算出模型参数.
1.4 引入控制点
为研究不同间隔控制点条件下的高程拟合精度,在试验现场分别获取同点位系列的两个钢轨GPS高程及水准高程,分析基于RTK的轨面GPS高程测量数据应用的可行性及数据处理方法.通过自动选取的结点建立的模型精度尚不能达到四等水准要求,因此需要引入另外的控制点来提高拟合模型精度.通过分别引入不同数量的控制点来提高限差精度,使模型的精度满足既有线勘测要求.
2 实例分析
2.1 工程概况
为了分析既有线在满足四等水准精度的要求下,在500 m间隔内用几个点作为基准点进行高程拟合是完全可行的.本文结合兰州某段既有线,以RTK、水准测量相互配合获取线路整体的三维数据,结合实例分别对平面模型、二次曲面模型进行验证.
本次试验测区内总共有已知控制点53个,在线路中,位于曲线内侧的内轨和位于曲线外侧的外轨分别有已知控制点25个,轨道附近水准点有3个.本文结合周围水准网的布设,自动选取解算模型参数所需的结点个数建立拟合模型,并将测区内拟合后的每1个点与四等水准进行精度评定.提出分别引入1~4个控制点来提高拟合模型精度,分析结果可行性.
2.2 高程拟合方案
GPS-RTK与连续运行参考站(CORS)联结组成控制测量网,水准测量组成四等水准测量网,为了提高测量数据可靠性和成果精度,需进行网平差与水准平差.
经网平差和水准平差后,可获得各点的水准高程,与GPS测得的GPS高程进行对比,可计算出高程异常.利用Matlab程序,分别采用平面拟合、二次曲面拟合法将高程异常进行处理,获得拟合后的GPS高程[15].两种情形下高程拟合对比情况如图1、图2所示.

图1 平面拟合模型高程对比图

图2 二次曲面拟合模型高程对比图
通过平面拟合和二次曲面拟合模型,算出的初步高程合格率尚不能达到要求.
2.3 试验控制点个数影响分析
由于自动选取最少结点形成的平面和二次曲面拟合模型精度未能达到四等水准要求,因此在此基础上引入1~4个控制点,分析GPS高程数据的可行性.
2.3.1 一个控制点实验分析
对本次试验所测500 m既有线区域内,引入线路内外轨始端1个控制点进行可行性研究,如图3所示.分别采用已建立的自动化平面和曲面模型进行高程拟合,通过计算可知,引入1个控制点后,平面拟合成果的内、外轨合格率均可达到92%,最大残差的绝对值达到了24.16 mm.二次曲面拟合成果的内外轨合格率达到92%,最大残差达到了24.3 mm,最小残差为0.23 mm.
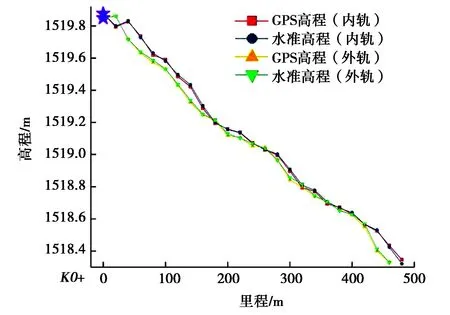
图3 内外轨各1个控制点拟合
2.3.2 两个控制点实验分析
对测区内各轨,依次引入线路首端和尾端2个控制点进行研究,图4中星号位置即为所选取的控制点.分别采用自动化平面和曲面模型进行高程拟合,引入2个控制点后,平面拟合成果的内轨合格率可以达到96%.外轨合格率可达100%,最大残差为14.0 mm.二次曲面拟合成果的内轨合格率可达96%,最大残差为14.88 mm,最小残差为1.32 mm.二次曲面拟合成果的外轨合格率可达100%,最大残差为14.0 mm,最小残差为0.54 mm.

图4 内外轨各2个控制点拟合
2.3.3 三个控制点实验分析
在500 m测区内,分别选取线路首、尾端各1个控制点,中间1个控制点进行限差评定,在图5中用星号表示.引入三个控制点后,分别采用自动化平面和曲面模型进行高程拟合,通过计算可知,平面拟合成果的内轨合格率可以达到96%,最大残差为14.76 mm.平面拟合成果的外轨合格率可达100%.二次曲面拟合成果的内轨合格率可达96%,最大残差14.05 mm,最小残差为1.0 mm.二次曲面拟合成果的外轨合格率可达100%,最大残差仅为12.2 mm,最小残差为0.49 mm.
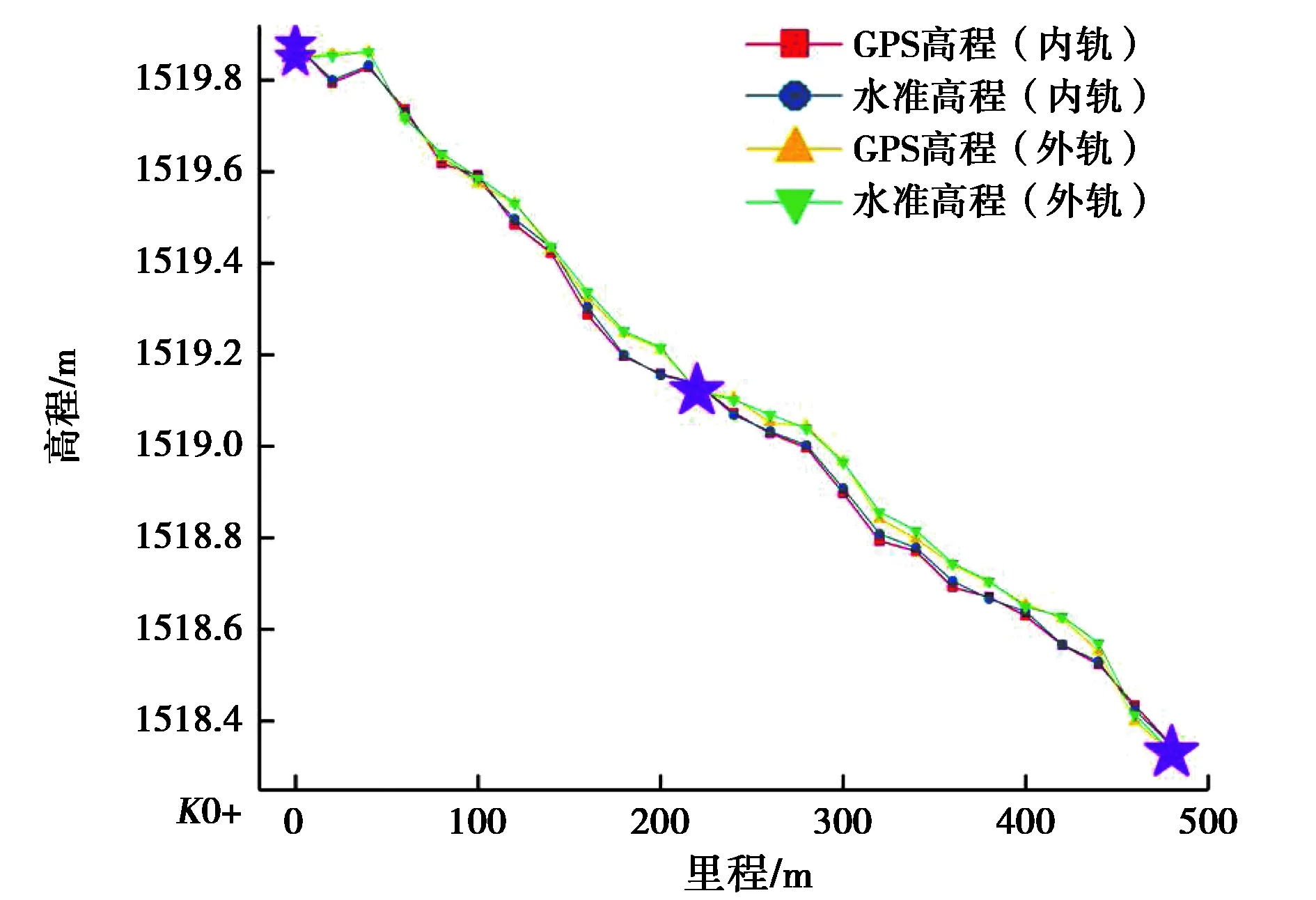
图5 内外轨各3个控制点拟合
2.3.4 四个控制点实验分析
引入线路首、尾端各1个控制点,中间选取2个控制点进行模型分析,在图6中星号位置即为所选取的控制点,分别采用自动化平面模型和曲面模型进行高程拟合,通过计算可知,平面拟合成果的内轨合格率可达100%,将所求残差取绝对值,最大残差为13.88 mm,最小残差为0.2 mm.平面拟合成果的外轨合格率可达100%,最大残差为14.0 mm,最小残差为0.03 mm.二次曲面拟合成果的内轨合格率可达100%,最大残差为13.00 mm,最小残差为0.14 mm.二次曲面拟合成果的外轨合格率可达100%,最大残差为13.85 mm,最小残差仅为0.11 mm.
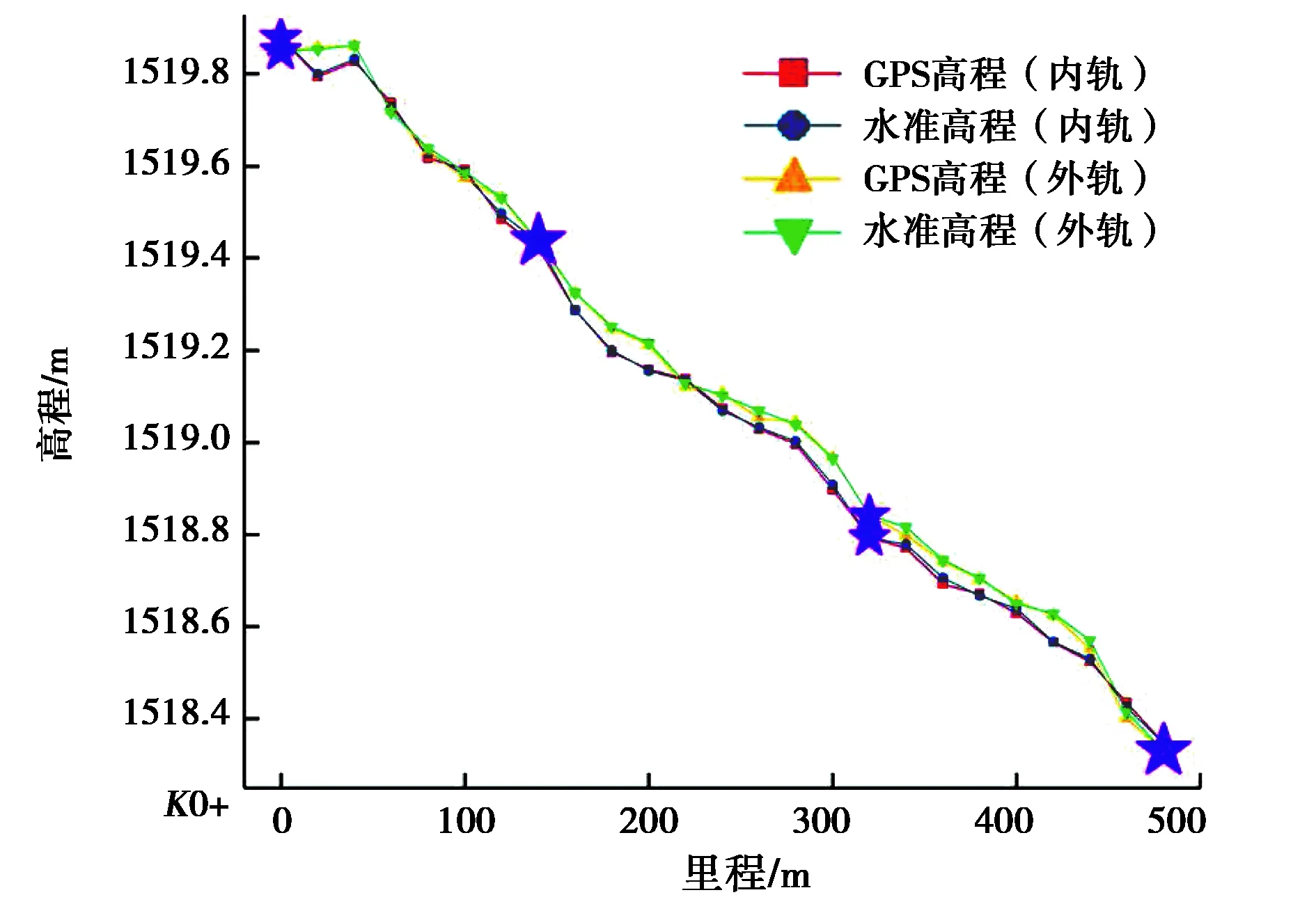
图6 内外轨各4个控制点拟合
3 结果比较
3.1 两种模型残差对比
在引入不同数量控制点条件下,对两种模型拟合后的结果进行残差分析,计算结果如图7~10所示.

图7 平面拟合下的残差对比图(内轨)
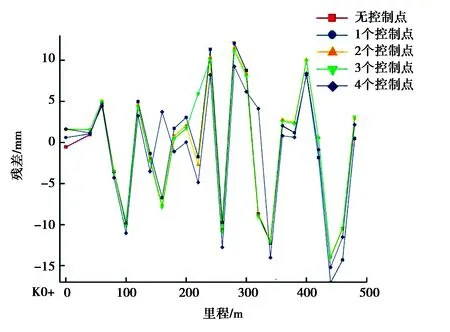
图8 平面拟合下的残差对比图(外轨)
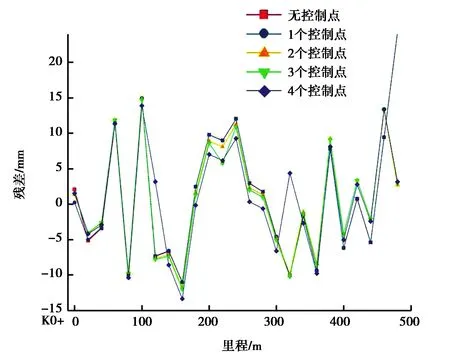
图9 二次曲面拟合下的残差对比图(内轨)
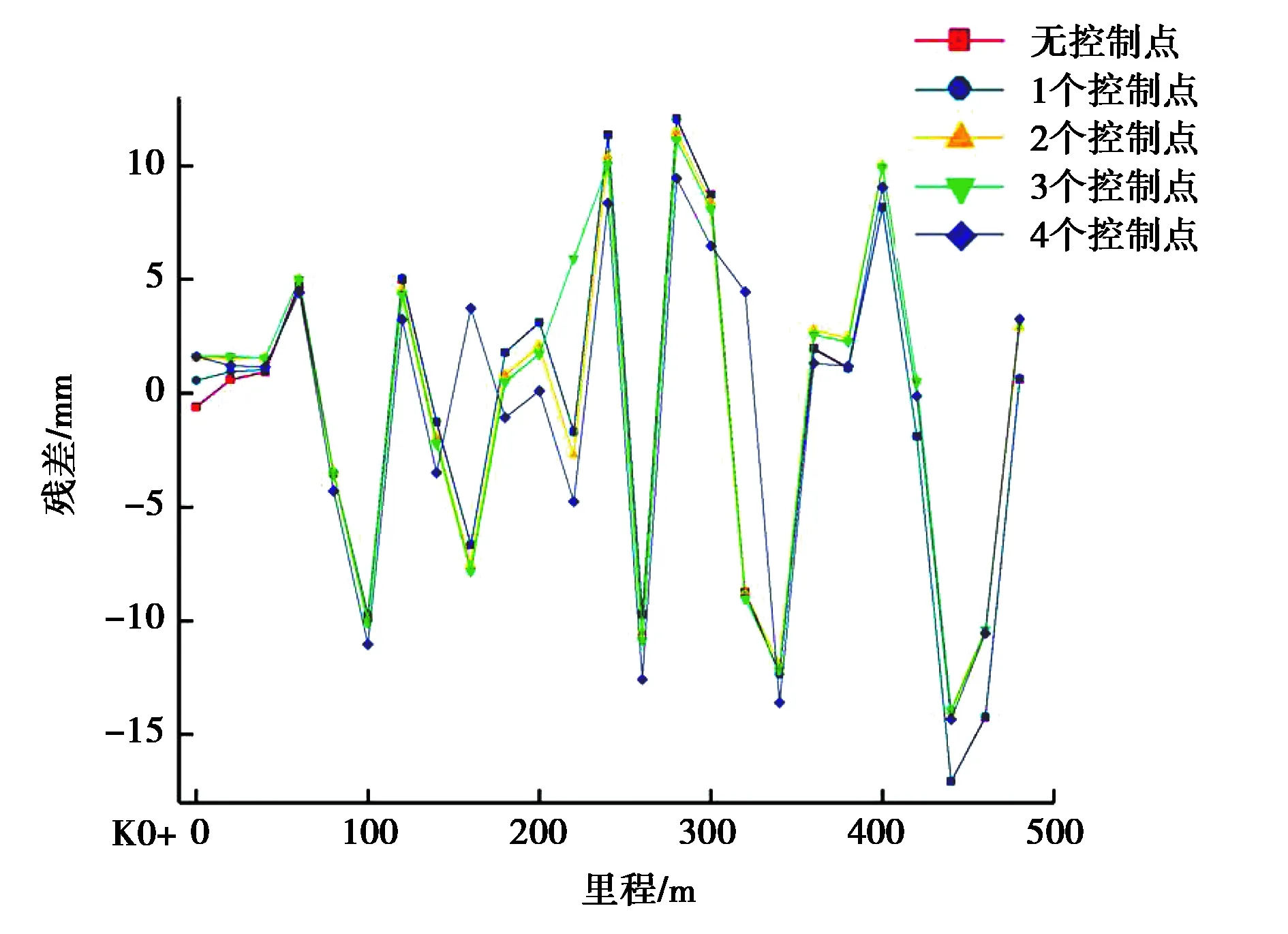
图10 二次曲面拟合下的残差对比图(外轨)
3.2 精度评定
通过引入控制点建立自动化平面及二次曲面拟合模型,分析内外轨合格率、最小最大残差值以及残差对比图,可知平面和二次曲面拟合模型在引入4个控制条件下均可达到四等水准要求.除此之外,还需要对两种模型的内外符合精度进行评价,从而再次判断模型的精确程度.
1)内符合精度
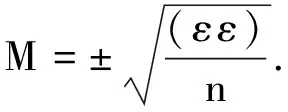
(8)
式中:ε为参与计算的已知点的拟合残差;n为参与计算的已知点个数.
2)外符合精度
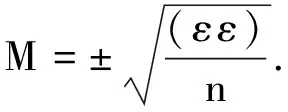
(9)
式中:ε为参与检核的已知点的拟合残差;n为参与检核的已知点个数.
本次试验的内、外符合精度计算结果如表1所示.

表1 两种模型精度对比

所以采用自动化二次曲面拟合模型进行高程拟合时,得到的拟合高程的合格率可达100%.当使用3个点作为基准点进行高程拟合时,合格率为96%,排除偶然误差后,则认为是可行的.且内外符合精度均达到要求.
4 结 论
本文针对GPS-RTK技术获得的高程数据转化为水准高程数据时精度较低的现象,提出一种自动化二次曲面拟合模型.基于兰州某段既有线进行不等间距实地测量,对现场实测数据通过引入不同数量控制点的情况下进行自动化二次曲面拟合,并分析拟合精度得出以下结论:
1)在500 m区间内,内外轨分别用3或4个控制点进行高程拟合,排除偶然误差后,结果符合四等水准限差要求.
2)在引入一定数量控制点条件下,在500 m间隔内采用自动化二次曲面拟合后得到的GPS高程数据可以较好地满足既有线勘测要求.
