地铁列车最优黏着控制研究

李会子， 郭其一

(同济大学 电气工程系， 上海 201804)

在交流传动地铁车辆牵引控制中，空转/滑行保护和黏着利用控制是牵引控制系统的一部分，统称为黏着利用控制系统。如图1所示，在线路轨面状况变化不定的情况下，比如轨面干燥、潮湿、雨雪等外界条件变化时，列车的牵引力不能得到有效利用，黏着利用控制系统的主要作用是通过对电机速度，电机转矩等信息的采集，分析和处理，综合得出电机转矩指令，向电机控制系统发出合适的电机转矩给定，使得列车能以接近线路当前最大的黏着系数运行，从而获得最大的黏着利用率。

文献[1]采用了相位法来间接测量黏着特性曲线斜率，根据线性系统理论，在电机转矩给定上叠加一定频率和幅度的正弦测相信号，使黏着利用效率可以达到80%以上，但是叠加信号产生的干扰将会影响电机控制性能[1]。文献[2]采用组合校正法，通过速度差和加速度与设定阈值比较来判断列车的运行状态，从而调节电机的转矩。但是组合校正法是在检测到列车发生空转/滑行之后动作的，黏着利用率较低[2]。文献[3]将滑模极值搜索算法应用到汽车ABS防抱死刹车系统中，补偿车辆转弯时的侧向稳定性，使车辆能够适应路面黏着系数的变化[3]。

永磁同步牵引系统具有节能环保的优点，针对地铁列车的最优黏着控制问题，考虑到永磁同步电机轴控技术的不断推广与应用。首先搭建了列车单轴动力学模型，设计全维状态观测器对轨面黏着系数进行估计，其次采用滑模变结构设计控制器对电机控制转矩进行调节，从而提高列车的黏着利用率。

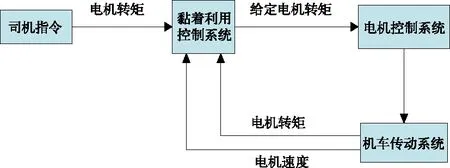
图1 黏着利用控制系统在传动控制中的位置

1 列车模型和轮轨黏着特性

1.1 列车单轴动力学建模

地铁列车的基本配置为6辆车编组，由4辆动车车辆和2辆拖车车辆组成。其中动车车辆装有动力牵引装置，车辆转向架上安装有牵引电机，由牵引电机将电能转换为机械能，通过齿轮箱传动轴传递到轮对上，产生列车前进所需要的黏着力。图2为列车轮轨黏着力牵引示意图。

图2 列车单轴黏着力示意图

齿轮箱的传动特性为：

(1)

车轮线速度与角速度之间有如下关系式：

vd=ωd·r

(2)

列车在牵引前进的过程中，车轮线速度与车体速度直线的差值定义为蠕滑速度：

vs=vd-vt

(3)

牵引电机的动态方程为：

(4)

负载转矩 满足如下关系式：

(5)

列车运动方程为：

(6)

基本阻力公式为：

Fd=((1.65+0.024 7×vt)×Mm+

(0.78+0.002 8×vt)×Mt+(0.028+0.007 8×

(N-1))×vt2)×9.8/1000

(7)

其中，ωm是牵引电机角速度;ωd是车轮角速度;vd是车轮线速度;vt是车体速度;vs是蠕滑速度;μ(vs)是轨面黏着系数;F是单轴列车模型轮轨之间产生的黏着力;Fd是列车运行的阻力;W是列车单轴轴重;M是整车质量;r是车轮半径;Rg是齿轮箱的传动比;Tm是电机电磁转矩;TL是电机负载转矩;Jm是归算到电机侧的等效转动惯量(即车轮和牵引电机转动惯量归算后的等效值);B是归算到电机侧的等效黏滞系数(即轮轴和电机轴摩擦黏滞系数归算后的等效值);Mm是列车动车自重;Mt是列车拖车自重;N是地铁列车的车辆数。

1.2 黏着特性曲线

轨面黏着系数可以反应轮轨间的接触情况，大量试验表明黏着系数与蠕滑速度之间的特性关系可以用式(8)表示：

μ(vs)=c·e-avs-d·e-bvs

(8)

其中a、b、c是轨面条件参数，表1给出了4种不同轨面下条件参数的取值。

不同轨面条件下黏着系数的最优值及该值对应的蠕滑速度计算公式如式(9)～式(10)

(9)

(10)

表1 不同轨面下的计算参数

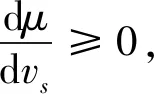
图3 黏着特性曲线

2 全维观测器的设计

根据车体的动力学方程可得到状态空间表达式如式(11)

(11)

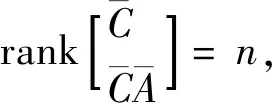
采用极点配置方法设计全维状态观测器：

(12)

图4 全维状态观测器

因此：

(13)

黏着系数的估计值为：

(14)

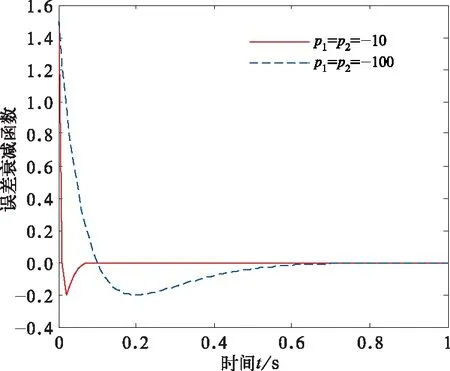
图5 不同极点下的误差衰减曲线

3 滑模变结构控制器的设计

3.1 滑模极值搜索最优蠕滑速度

为了提高列车的黏着利用率，黏着利用控制系统采用滑模极值搜索算法搜索出当前轨面下的蠕滑速度最优值，使黏着系数尽可能达到最大。

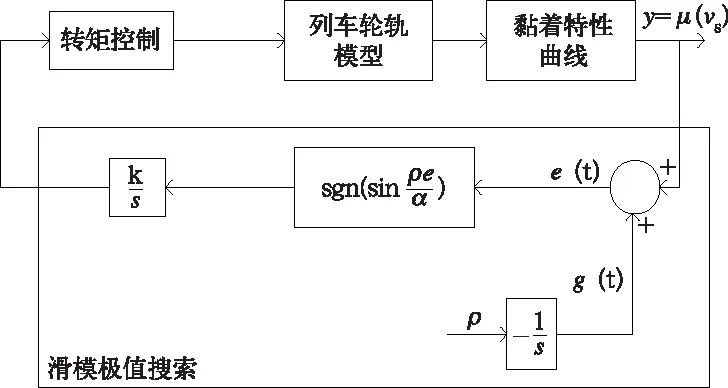
图6 滑模极值搜索算法原理图

设切换函数为：

e(t)=y(t)-g(t)

(15)

(16)

选择最优蠕滑速度观测值的导数为控制律：

(17)

将式(17)带入到式(16)中可得：

(18)

存在一个常数C，满足：

(19)

那么滑模运动将会发生在e(t)=C的滑模面上。

(1)当e(t)定义域为[(n-1)α,nα]时，

(e(t)-nα)·(e′(t)-nα)=(e(t)-nα)×

(20)

(e(t)-nα)·(e′(t)-nα)<0

(2)当e(t)定义域为[nα，(n+1)α]时，

(e(t)-nα)·(e′(t)-nα)=(e(t)-α)×

(21)

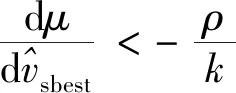
(e(t)-nα)·(e′(t)-nα)<0

3.2 滑模变结构转矩控制器的设计

通过滑模极值算法跟踪得到当前轨面条件下的最优蠕滑速度值，需要对电机转矩进行控制使列车可以以最优蠕滑速度运行，从而最大化的利用轨面的黏着率。由于滑模变结构针对带有不确定性和外加干扰的系统可以通过设计控制率来实现较强的鲁棒控制，因此下面将实现等效控制来实现列车的转矩控制。

定义滑模面为 ：

s(t)=vs-vsbest

(22)

(23)

当蠕滑速度达到最优蠕滑速度时，则满足s(t)=0，s′(t)=0。

为使系统可以一直稳定在滑模面上运动，采用等效控制ueq为基础的形式来设计控制律。

(24)

(25)

(2)当系统不在滑模面上运动时，需要加入一个控制信号来使系统的状态趋近于滑模面运动，最终稳定在滑模面上。

Tm=u=ueq-q·sgn(s(t))

(26)

将式(25)代入到式(23)中得：

(27)

该控制律使系统最终可以稳定在滑模面上：

(28)

4 仿真与分析

在MATLAB/Simulink中根据控制系统框图搭建单轴列车传动过程中的黏着控制系统仿真模型。地铁列车的仿真参数如表2所示。

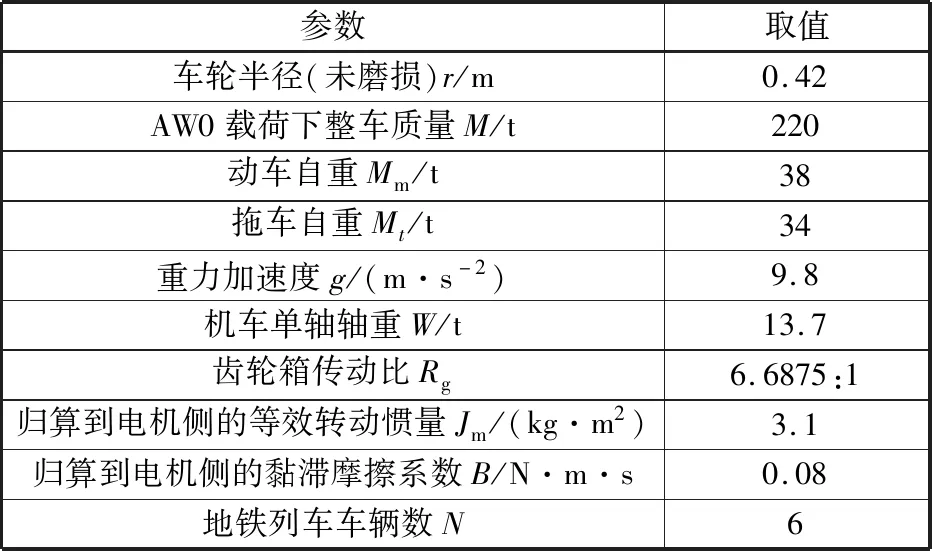
表2 地铁列车参数(上海地铁13号线)

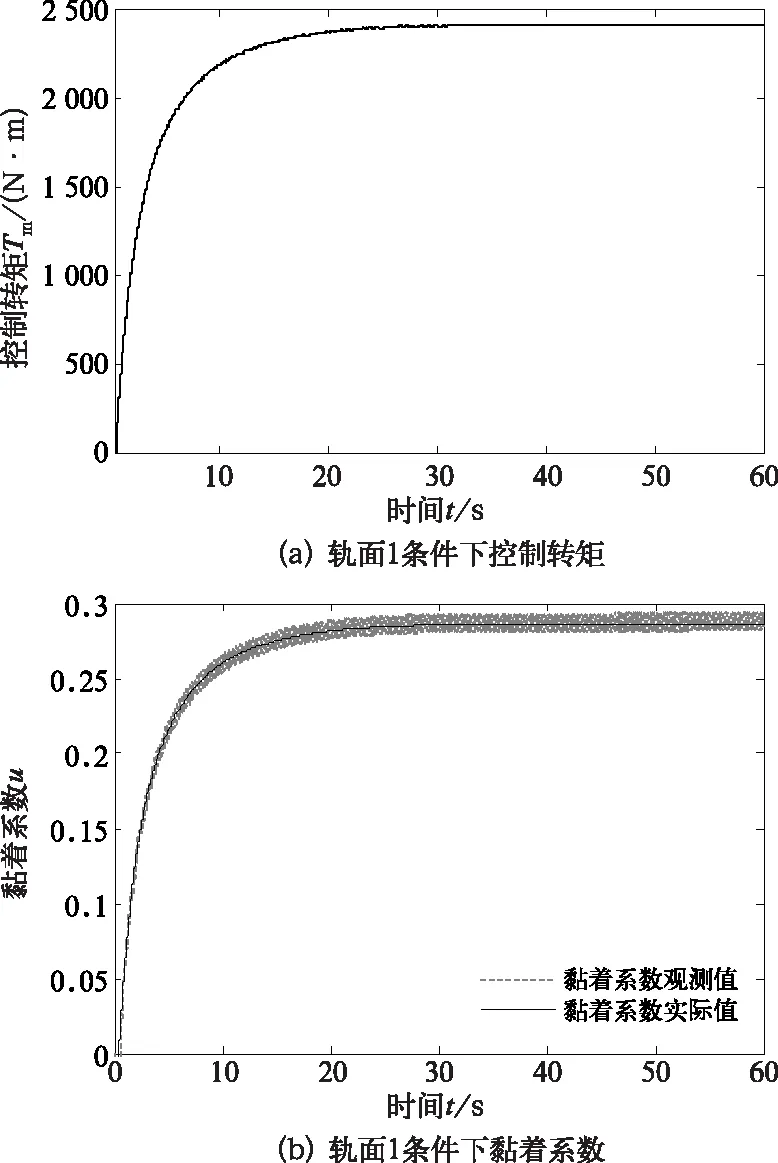
图7 轨面1条件下黏着控制仿真结果

从图7(a)中可以看出，当列车运行在轨面1上启动并加速的过程中，如果司机给定转矩指令为3 000 N·m，列车在20 s时控制转矩Tm可以达到2 400 N。图7(b)中此时黏着系数达到0.28，随后稳定在0.28附近，充分利用了黏着率。

图8 不同轨面条件下黏着控制仿真结果

图8中实现的是在不同轨面条件下进行切换的过程，整个仿真时间为90 s。在0～40 s，列车运行在轨面1的条件下，控制转矩和黏着系数的仿真结果和图7所示相同。在40～70 s，列车切换到轨面3运行，由于黏着系数突然下降，因此电机控制转矩在段时间内快速调整，减小并稳定在1 200 N ，黏着系数大概在0.14。避免空转滑行的同时充分利用了黏着率。在70～90 s的时间段，切换到轨面2运行，黏着系数增加，因此电机控制转矩调整到1 600 N ，此时黏着系数稳定在0.19左右。总体来看，控制转矩和黏着系数随轨面变化情况一致，在不同轨面下进行切换时可以快速调整到最优蠕滑速度下运行，提高黏着利用率。

5 结 论

设计了滑模变结构控制器，用来对地铁列车的电机转矩进行控制调整。并基于MATLAB/Simulink对地铁列车的单轴牵引模型进行仿真，对不同轨面条件下的最优蠕滑速度进行搜索，提高了黏着利用率，实现了最优黏着控制。最近一段时期，基于永磁同步电机的轴控技术在推广应用，以及车载计算机的性能不断提升，该控制技术可以付诸实践与应用。