薄壁箱梁剪力滞效应的有限梁段分析

罗文权，蔺鹏臻

（1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃兰州 730070；2.兰州交通大学 土木工程学院，甘肃兰州 730070）

箱形薄壁梁在对称荷载作用下，法向应力沿横截面的分布是不均匀的，对于闭口截面，称之为剪力滞效应［1］。对于剪力滞的计算，国内外的分析方法有能量变分法、比拟杆法、有限条法和板壳有限元法。能量变分法中，剪滞翘曲位移函数的选取是关键，Reissner［2］假设翼板剪滞翘曲位移函数为二次抛物线，在横截面上引入一个翼板剪切变形最大差φ，从而建立了矩形双轴对称箱梁剪力滞效应的变分解。Luo［3］选取能量变分法导出控制微分方程的齐次解作为梁段单元的有限元位移模式，在变分原理的基础上提出分析箱梁剪力滞效应的有限梁段法。吴幼明等［4］针对单室箱梁，通过在横截面分别引入顶板、悬臂板、底板3 个不同的剪滞翘曲位移函数来分析剪力滞效应。Zhou［5］通过定义每个节点有2个剪力滞自由度的有限元法来分析剪力滞效应，并进一步分析预应力混凝土箱梁的剪力滞效应，周朋等［6］在此基础上研究了不同荷载形式下箱梁的剪力滞效应。张元海等［7］选取剪力滞效应引起的附加挠度作为广义位移，在定义新剪力滞广义力矩［8］的基础上，将剪力滞变形作为独立的变形状态进行有限元分析。

本文在文献［3］的基础上选取基于翼板剪切变形规律而定义的翘曲位移函数，将其控制微分方程的齐次解作为梁段单元的有限元位移模式，再根据变分原理导出薄壁箱梁的单元刚度矩阵和荷载矩阵，从而得到考虑剪力滞效应的薄壁箱梁的挠度和应力。

1 基于剪切变形规律的翘曲位移函数

在竖向荷载作用下，假定薄壁箱梁（见图1）的腹板仍符合梁的平截面假定，不考虑腹板的剪切变形；上下翼板、腹板的竖向纤维挤压变形、板平面外的剪切变形及横向应变均很小，可以忽略。

图1 薄壁箱梁（半截面）

定义ω(x)为截面上任一点(x，y，z)的竖向挠曲位移，θ(x)为相应的转角，u(x，y，z)为纵向位移函数，φ(x)为翼板剪切变形最大差，f(y，z)为截面的剪滞翘曲位移函数。线位移以图1 坐标方向为正向，转角以顺时针为正向。横截面的纵向位移可表示为

基于剪切变形规律的翘曲位移函数［9］

式中：ξ2=S2/S1，即悬臂板和内侧顶板面积之比；ξ3=Zx Ax/(ZsAs)，Ax为下翼板面积，As为上翼板（内侧顶板加悬臂板）的面积。

2 梁段单元的位移模式

引入竖向弯曲惯性矩I、全部翼板的剪滞翘曲惯性矩Iu、全部翼板的剪滞翘曲惯性积Iyu和全部翼板的剪滞翘曲面积Au等广义截面特性［10］后，基于能量变分法，得到ω(x)，φ(x)关于薄壁箱梁梁段剪滞基本微分方程的齐次解为

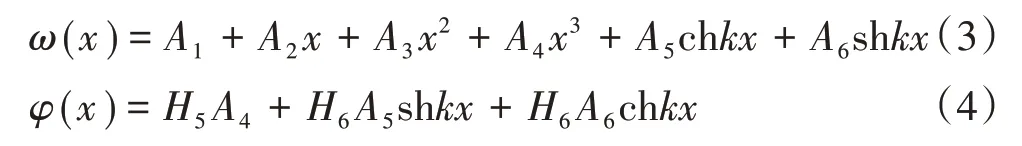
考虑薄壁箱梁剪力滞影响的梁段单元（见图2）的节点位移向量可表示为

当x= 0时，ω(0)=ωi，θ(0)=θi，φ(0)=φi；当x=l时，ω(l)=ωj，θ(l)=θj，φ(l)=φj。因此，式（3）和式（4）可分别表示为

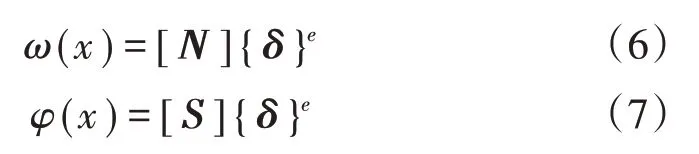
式中：［N］和［S］均为形函数，［N］=［N1N2N3N4N5N6］，［S］=［S1S2S3S4S5S6］。

图2 梁段单元

3 梁段单元刚度矩阵和荷载列阵

根据截面任一点的纵向位移，得到截面的弹性应变为

梁段单元的应变能可表示为对梁段体积的积分

将式（6）和式（7）代入式（9）可得

由最小势能原理，通过变分得到

单元刚度矩阵为

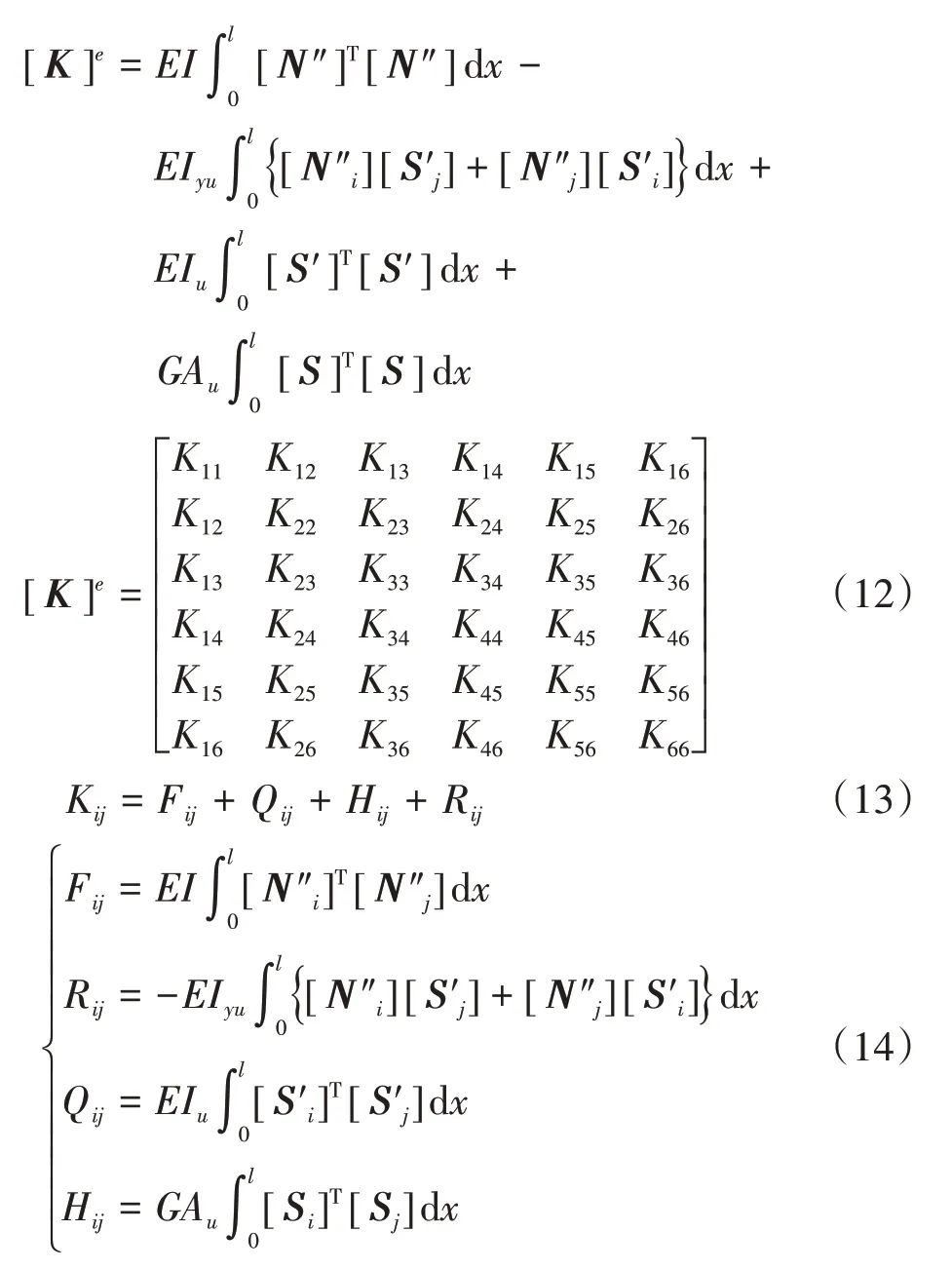
其中，i，j= 1，2，3，4，5，6。

荷载列阵为

由式（8）按胡克定律得梁段的应力公式为

剪力滞系数定义为

4 算例对比

以文献［1］中的箱梁截面为例，截面尺寸见图3。弹性模量31 GPa，泊松比为1/6。不计自重的情况下，分别在跨中作用1 000 kN的集中荷载和满跨1 000 kN/m的均布荷载。

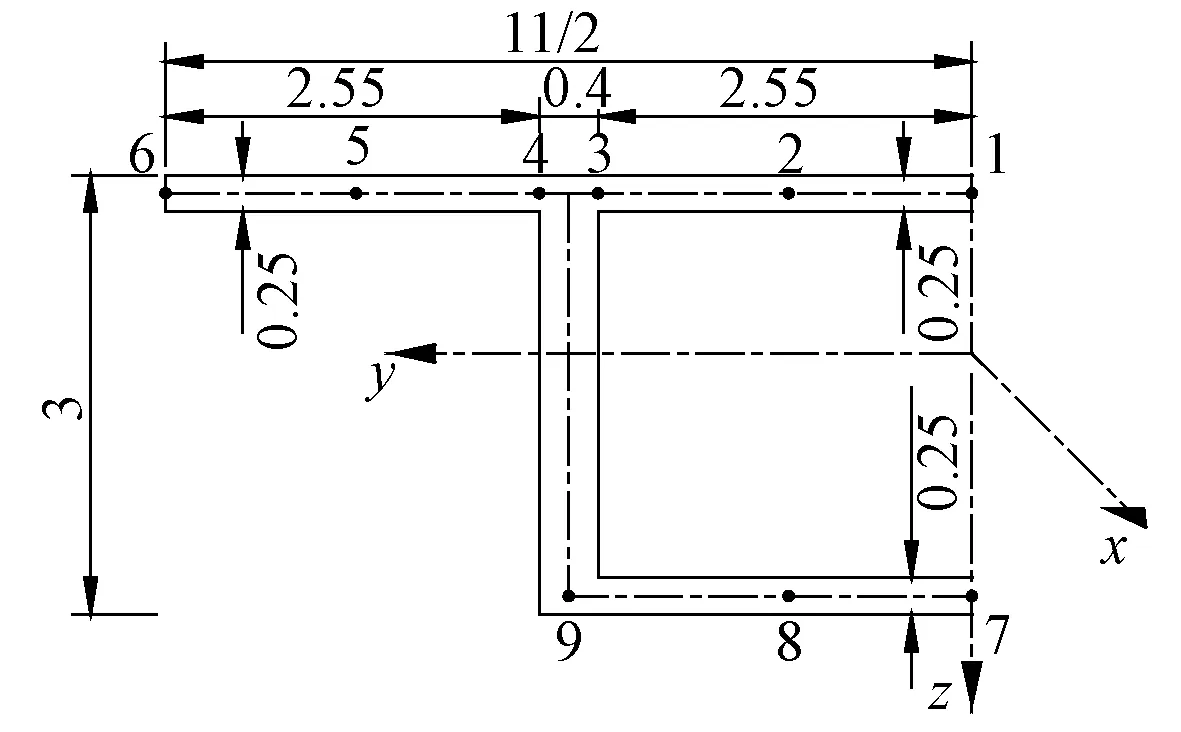
图3 箱梁尺寸（半截面）（单位：m）

4.1 等截面简支箱梁

通过MATLAB 编程求得简支梁在均布荷载作用下的挠度，并将计算结果与初等梁解及文献［11］解对比，见图4（a）。改变荷载矩阵，计算得到集中荷载下简支梁沿梁纵向的挠度，见图4（b）。

图4 简支梁纵向挠度对比

由图4 可知：本文解与文献［11］几乎完全一致。与初等梁解相比，本文考虑了剪力滞的影响，2种荷载作用下计算的挠度在跨中分别增大了7.49% 和8.60%。

按式（16）计算得到跨中截面纵向应力。采用ANSYS 有限元软件建立板壳模型进行数值计算，并与文献［12］解析结果进行对比，见表1。同理可得集中荷载作用下的应力，见表2。

由表1 和表2 可知：本文解与文献［12］解几乎完全一致，并且与ANSYS 有限元数值解吻合良好，均布荷载下跨中截面上翼板和下翼板的剪力滞系数最大值分别为1.071 1 和1.075 3；集中荷载下的剪力滞系数最大值则均为1.260 6。

4.2 等截面悬臂箱梁

通过MATLAB 编程求解与简支梁相同截面形式的悬臂梁作用均布荷载时的挠度，并与初等梁解及文献［11］解进行对比，见图5。

表1 均布荷载下跨中截面纵向应力

表2 集中荷载下跨中截面纵向应力

图5 均布荷载下悬臂梁纵向挠度

按式（17）可计算全跨顶板在y= 0 和y=b1处的剪力滞系数，并与文献［12］解对比，见图6。

图6 均布荷载下悬臂梁顶板剪力滞系数沿梁纵向分布

由图5 和图6 可知：悬臂梁作用均布荷载时，本文解与文献［11］几乎完全一致；与初等梁解相比，本文计算的挠度在自由端增大了3.11%；本文计算的沿梁纵向剪力滞系数与文献［12］解几乎完全一致，其中在固定端截面顶板y=b1处剪力滞系数为1.241 9。

5 结论

1）薄壁箱梁的剪力滞效应是由翼板剪切变形而引起的，根据这一基本机理定义的翘曲位移函数更符合实际。

2）与初等梁解相比，在均布荷载和集中荷载作用下，考虑剪力滞效应后简支梁的挠度在跨中分别增大了7.49%和8.60%；在均布荷载作用下，悬臂梁在自由端挠度则增大了3.11%。

3）在均布荷载下简支梁上翼板和下翼板最大剪力滞系数分别为1.071 1 和1.075 3；集中荷载下则均为1.260 6；均布荷载下悬臂梁固定端截面处剪力滞系数为1.241 9。可知，剪力滞效应对薄壁箱梁截面纵向应力影响较大，在设计与施工时应加以重视。