非对称粗糙带对单圆柱流致振动特性影响研究
2019-11-09章大海王文颢李天娇
章大海, 王文颢, 李天娇, 冯 蕾, 孙 海
(1. 中国石油大学(华东) 化学工程学院, 山东 青岛266580; 2. 哈尔滨工程大学航天与建筑工程学院, 哈尔滨150001)
0 引 言
当一定速度的流体绕流柱体结构时, 交替脱落的不对称旋涡对柱体横向及流向产生周期性作用力,进而引发柱体振动,柱体振动又反过来影响其尾涡脱落及形态,这种结构与流体之间的相互作用问题就称为流致振动(Flow-Induced Vibration,FIV)。它是一种广泛存在于工程应用和自然界中的重要现象,常见的流致振动现象包括涡致振动(Vortex-Induced Vibration,VIV)、颤振(Flutter)、抖振(Buffeting)和驰振(Galloping)等[1]。流致振动会导致高烟囱、海洋油气输送管线和海上平台等建筑物产生疲劳破坏。 在近几十年核工程、航空航天工程和海洋工程等迅速发展的背景下,流致振动因重大危害性而受到了高度关注[2],比如1940 年Tacoma 吊桥在较低风速下产生颤振失稳而倒塌。 早在1968 年,Feng[3]就弹性安装的光滑圆柱涡致振动进行了一些重要的经典测量,得到的振幅比曲线包括“初始分支”和“下分支”,这个定义是由Khalak 和Williamson[4]给出的,他们得到的涡致振动振幅比曲线包括“初始分支”、“上分支”、“下分支”和“去同步化”四部分,得到这种结果的主要原因是Feng 的实验介质为空气,而Khalak 和Williamson 的实验介质为水。 涡致振动可在一定条件下转化为驰振,驰振有大振幅和小频率的特点[5]。 Bokaian 和Geoola[6]指出钝体为非圆柱结构即为方柱等结构可以激发驰振,同时Bokaian和Geoola[7]研究表明当一个圆柱靠近其他圆柱时也可以激发驰振。 Achenbach[8]则表示圆柱外表附有粘贴物可使涡致振动进一步激发为驰振, 这种通过在圆柱表面粘贴附属物来控制流致振动的方法称为被动湍流控制(Passive Turbulence Control,PTC)。 为了更好地理解存在PTC 的物理现象,一些研究者把注意力转向了二维几何分布,研究带有对称或不对称PTC 的单个圆柱,是了解更复杂的结构所涉及物理现象的一个重要过程。 Nebres 与Batill[9]研究了带有单个金属线圆柱的频率响应,发现旋涡脱落频率在一定范围内随着金属线分布角度而改变。 Ekmekci 与Rockwell[10]确定了基于近尾特性的单个金属线圆柱两个重要分布位置(θc1=55°和θc2=65°),他们发现在Re=10 000 时,金属线(d/D=0.029)置于θc1可以扩展顺流向的尾流气泡长度,而置于θc2会收缩;他们还发现当金属线直径大于未扰动的边界层厚度时,放置在θc1会明显减小冯·卡门频率下的速度波动的频谱幅度,并且当同一导线处于θc2时,会产生相反的效果。
流致振动不只是会带来前文提到的危害,它也能造福于人类。 在2006 年,密歇根大学海洋可再生能源实验室(Marine Renewable Energy Laboratory,MRELab)的Bernitsas 等[11]提出涡致振动水生清洁能源系统(Vortex Induced Vibration for Aquatic Clean Energy, VIVACE),把涡致振动和海洋能发电技术相融合,使这类潜在的危害性转变为能量的利用。 在之后的研究中,Bernitsas 和Raghavan[12]以选择性表面粗糙度的方法来加强圆柱的振动,进而增大能量输出,并且取得了良好的效果。Chang 等[13]对对称粗糙带单圆柱的流致振动做了大量研究, 得到了不同规格对称粗糙带下的振幅及功率等数据。 2011年,Park[14]等在MRELab 对对称粗糙带的分布位置进行大量实验,进而建立了PTC-TO-FIV 图,为对称粗糙带的选择提供了参考依据。 近几十年来,随着计算机技术飞速发展,计算流体力学(CFD)也被广泛应用,因为实验可测量参数有限,CFD 作为补充就必不可少。 Kinaci[15]以k-omega SST 湍流模型研究了光滑单圆柱的流致振动现象,得到了其振幅及频率曲线,并与Khalak 和Williamson[16]的实验数据进行了对比,捕捉到了不同的振动区间。 Ding[5]等采用CFD 和实验研究了对称粗糙带单圆柱流致振动特性,对比了两者的振幅、频率和功率等,也捕捉到了非对称的尾涡结构。
然而近年来相关的研究主要集中在雷诺数40 000 以下[17],更高雷诺数下的流致振动研究较少,对于非对称PTC 圆柱的研究多见于静止圆柱,而非对称PTC 圆柱的流致振动研究较少,在MRELab 进行的圆柱流致振动研究全部集中于对称粗糙带,对于非对称粗糙带更是尚未见报道。 这种方式是否会造成大的振幅进而产生更大的输出功率,其尾涡模式又如何,这些都是未知的,而且进一步将对称和非对称粗糙带圆柱及光滑圆柱的流致振动数据进行对比,对更好理解粗糙带的作用机理有很大帮助,也为理解更复杂结构的流致振动机理做铺垫。 所以, 本文采用二维非定常RANS 方法和Spalart-Allmaras 湍流模型,结合ANSYS-Fluent 软件动网格技术和用户自定义(UDF)功能,对大范围雷诺数的非对称粗糙带单圆柱流致振动进行数值模拟研究, 并与来自美国密歇根大学海洋可再生能源实验室的实验结果对比,研究结果具有较为重要的科研意义和广阔的应用前景。
1 计算模型
本文采用商业CFD 软件ANSYS-Fluent 对非对称粗糙带单圆柱进行数值计算。
1.1 几何模型
本文的计算区域为矩形,如图1 所示。 与实验参数一致[18],取圆柱直径D 为88.9 mm,整个计算区域的长为40D=3 556 mm,深为14D=1 244.6 mm,圆柱中心位于入口处15D=1 333.5 mm,并且关于上下壁面对称。
圆柱的非对称粗糙带布置如图2 所示,圆柱上用高为0.847 mm 的小凸台来模拟粗糙带,小凸台布置位置为α=20°,且覆盖范围为θ=16°。
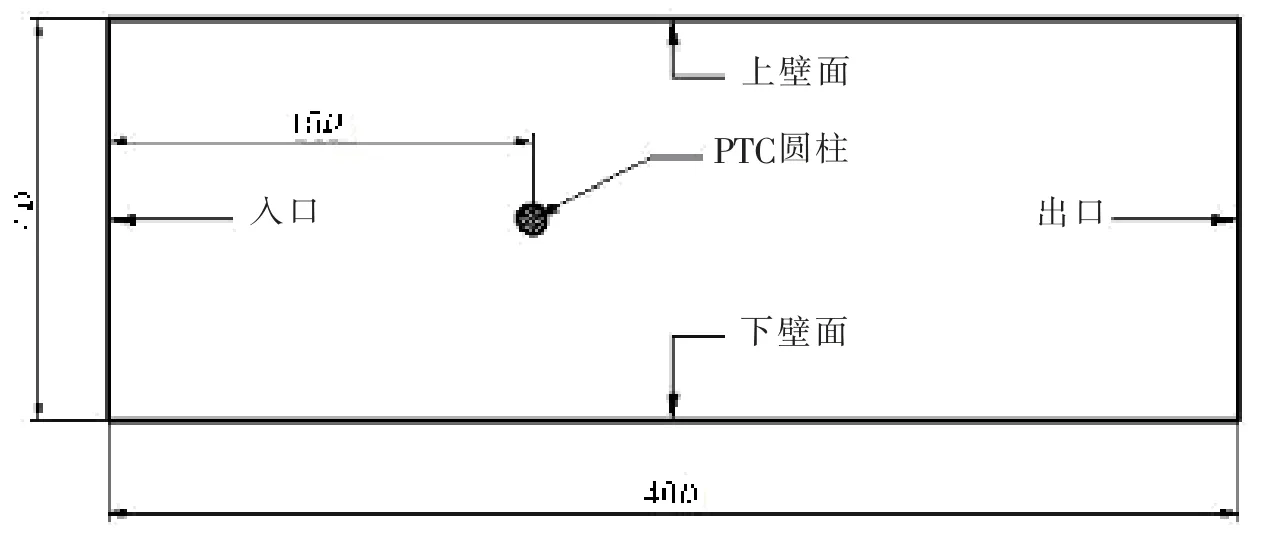
图1 计算域示图Fig.1 Computational domain diagram

图2 粗糙带分布图Fig.2 ONE side PTC distribution
1.2 数学模型
对整个计算域二维非定常不可压缩粘性流体,其雷诺时均方程采用Spalart-Allmaras 湍流模型[19],可表示为如下方程:

式中:xi为笛卡尔直角坐标,ui为对应的速度分量,ν 为分子运动粘度,t 为时间,ρ 为流体的密度,τij为雷诺应力张量,Sij为平均应变率张量,其表达式为:

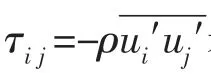

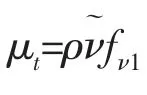
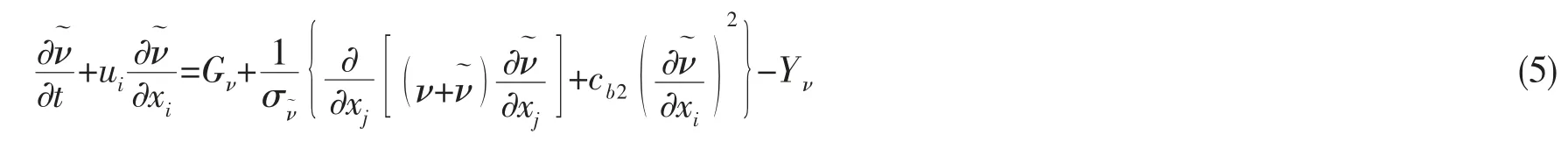

1.3 物理模型
本文采用经典的弹簧-质量-阻尼振子模型[20]来描述单圆柱振子的动力特性,单自由度运动方程可以表示为:

式中:m 为系统质量,c 为系统阻尼,k 为系统刚度,FL为圆柱总升力。
一个周期内的平均功率可表示为:

将经典的弹簧-质量-阻尼振子模型的公式(6)代入可得:

为了简化公式,从理论上求得可获得的功率,对刚性圆柱的响应假定为近似正弦,则可以表示为:

式中:A 是振幅,δ 是位移曲线的平衡位置与y=0 的偏差,ω 为振动圆柱的角频率且ω=2πf, f 为圆柱振动频率。 将位移求导可得速度为:

于是功率可简化为:

经积分可得VIVACE 系统的输出功率表达式为:

1.4 边界条件设定
将所建立的几何模型划分为五个区域,如图3 所示。
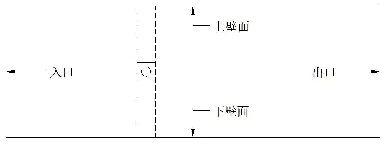
图3 几何模型整体分块图Fig.3 Block diagram of geometric model

图4 网格示意图Fig.4 Grid diagram
对如图3 所示的边界条件设置为:
(1) 入口为速度入口(Velocity inlet);
(2) 出口为出流(Outflow);
(3) 上壁面、下壁面和圆柱为固体面(Wall);
(4) 圆柱上下位置的实线为内部面(Interior);
(5) 虚线为交界面(Interface)。
1.5 网格划分及验证
本文在整个区域采用二维结构化网格,如图4 所示,在圆柱四周划分了2D×2D 的正方形网格区域,将正方形区域使用实面拼接分块并对圆柱附近进行局部加密,在小凸台高度方向划分了两层。 参考Ding[5]的网格无关性,考虑了相同三种不同疏密程度的网格,对静止圆柱做了雷诺数为30 000 的网格无关性验证,其结果如表1。结果表明,三种网格密度的升力系数最大值Cl 和阻力系数平均值Cd 相差较少,为加快计算速度,本文最终采用较稀网格进行计算,网格总数为94 932,Ding 的网格总数为60 252,可认为结果具有网格无关性。

表1 网格无关性验证Tab.1 Grid resolution study
1.6 UDF 及动网格设定
本文在UDF 中编写振动方程,对公式(6)采用迭代方法如下:

其中在UDF 里直接赋予m=7.826 kg,k=600 N/m,c=2.64 Ns/m 和c=18.5 Ns/m,FL利用UDF 程序中begin_f_loop( f, t)宏对圆柱表面压强积分得到,y 利用F_CENTROID(x, f, t)宏函数得到,y˙n和y¨n由公式(13)-(15)得到,在起始时刻定义为y1=0 及y˙1=0。
导入并加载UDF 之后,开启动网格,选择铺层形式,实现了结构化网格铺层形式,相对于非结构化其他形式,生成网格简单迅速,避免了大面积的网格重构,节省了资源的同时又有较高的精度。 其网格运动如图5 所示,图5(a)为PTC 圆柱初始时刻的网格图,图5(b)为PTC 圆柱运动到某一时刻的网格,可明显看出运动后网格铺层产生的网格层。

图5 网格运动示意图Fig.5 Grid motion diagram
1.7 参数说明
本文在数据处理中,对一些参数进行了如下无量纲化:
式中:U 为来流速度, fn,w为圆柱固有频率。
2 结果与讨论
2.1 振幅响应
如图6 为c*=0.02 且U*=10.28 的位移比响应过程曲线。 从图中可以看出,非对称粗糙带圆柱位移比响应过程曲线相对于平衡位置有约0.2 的偏移量,这就表示非对称粗糙带圆柱在正负方向的振幅值不同,而且表现为粗糙带侧的振幅小于另外一侧,这一结论与对称粗糙带圆柱的对称振幅是不同的。 在本文的数据处理中,为方便比较及讨论,后文出现的非对称粗糙带振幅均取正负向幅值的平均值。
如图7 所示为c*=0.02 时不同来流速度的光滑圆柱、非对称粗糙带圆柱和对称粗糙带圆柱流致振动实验振幅比曲线,图中纵轴给出的为振幅比A/D,横轴为雷诺数Re、来流速度U 和约化速度U*。

图6 位移比响应过程曲线Fig.6 Displacement response process
随来流速度增大,光滑圆柱流致振动振幅比曲线依次捕捉到初始分支、上分支、下分支;与光滑圆柱不同, 对称和非对称粗糙带圆柱依次捕捉到初始分支、上分支、过渡分支和驰振分支;粗糙带对于上分支有明显的拓宽作用, 光滑圆柱上分支范围约为5.5≤U*≤7.2,而粗糙带圆柱约为5.0≤U*≤8.6;与光滑圆柱不同,粗糙带圆柱振幅比曲线在上分支之后进一步增大,而非进入下分支;在上分支, 非对称粗糙带圆柱振幅比大于对称粗糙带圆柱, 而在驰振区情况是相反的; 相对于对称粗糙带, 可看出非对称粗糙带对于分支的分布范围影响不大。
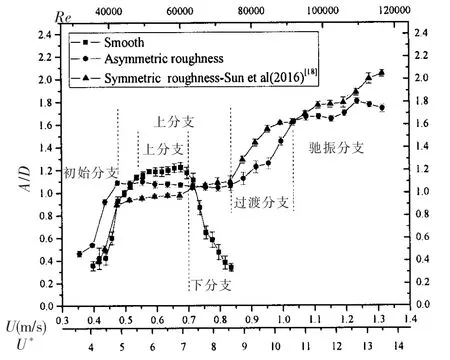
图7 振幅响应曲线Fig.7 Amplitude response
进一步对比不同阻尼下的非对称粗糙带单圆柱流致振动数值模拟和实验结果,图8 为c*=0.02和0.14 时的非对称粗糙带单圆柱实验与数值模拟振幅比曲线。 从图中可观察到较明显的几部分区域:
(a) 在Re<40 000~44 000 范围内捕捉到了初始分支,c*=0.02 时,实验圆柱的振幅增大到1.1D;c*=0.14 时,实验圆柱的振幅增大到0.9D。数值模拟比实验更早地开始振动,主要是由于数值模拟采用简化的弹簧-质量-阻尼模型,而实验中的模型为一种更复杂的粘性非线性模型。
(b) 在40 000~44 000≤Re<70 000~74 000 范围内捕捉到了上分支,也就是涡致振动(VIV)区,c*=0.02 时,实验圆柱的振幅保持在1.1D 左右;c*=0.14 时,实验圆柱的振幅保持在0.9D 左右,而数值模拟的振幅保持缓慢连续增长。
(c) 在70 000~74 000≤Re<90 000 范围内捕捉到了上分支-驰振过渡分支,c*=0.02 时,随着Re的增大,实验圆柱的振幅比从1.1D 增大到1.2D;c*=0.14时,实验圆柱的振幅0.8D 减小到0.7D。 图中给出的为多次实验的平均结果, 在此区间内振幅比标准偏差相对较大,说明过渡期振动不稳定,这就造成数值模拟捕捉的困难, 数值模拟在此区间和实验吻合不好也能归因于URANS 湍流模型不能预测随机小涡。 需要指出的是,在Kinaci[21]和Wu[22]等模拟研究中,过渡区也没有很好地吻合。
(d) 在90 000≤Re<120 000 范围内捕捉到了驰振分支, 随着Re 的增大,c*=0.02 时圆柱振幅从1.2D迅速增大到1.7D;c*=0.14 时从0.7D 迅速增大到1.3D。在驰振区前段,实验与数值模拟吻合良好,后段实验圆柱的振幅小于数值模拟的振幅是因为实验中到达了安全停止位置,这样做的目的是保护实验装置,同时实验中自由液面的影响也限制了圆柱振幅的进一步增加。

图8 振幅比曲线Fig.8 Amplitude ratio curve
从整体来看,数值模拟结果和实验结果大体吻合,能够很好地表现出与实验相对应的整个来流速度变化范围内的振幅变化,在每种系统阻尼比下,非对称粗糙带单圆柱流致振动实验振幅比曲线依次经历初始分支、上分支、上分支-驰振过渡分支和驰振分支,但数值模拟捕捉上分支不明显;阻尼增大使得非对称粗糙带单圆柱流致振动的振幅下降。 另外,在进入驰振分支后的振幅突然增大也符合驰振大振幅的特点。
2.2 频率响应
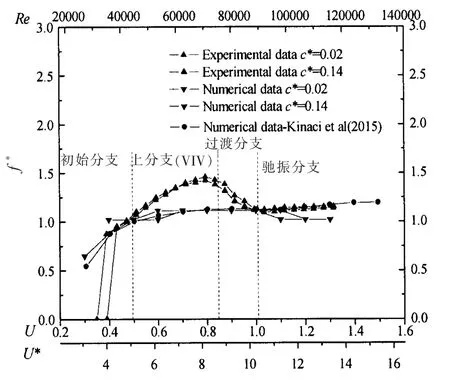
图9 频率比曲线Fig.9 Frequency ratio curve
图9 为c*=0.02 和0.14 时的实验与数值模拟频率比曲线。 频率比曲线的区域与振幅比曲线对应,数值模拟结果和实验结果趋势大体吻合,除上分支区外,频率比捕捉较为准确;阻尼对于非对称粗糙带单圆柱流致振动频率的影响不大。在上分支区,实验与数值模拟存在较大误差,在众多的研究中,这是雷诺时均方法存在的缺陷,这也是在相关领域模拟中广泛存在的问题,在Kinaci[21]和Wu[22]等文章中存在同样的问题,图9 中给出了Kinaci 的数值模拟曲线。 另外,在进入驰振区,实验中的f*下降并稳定于1.1,数值模拟的f*下降并稳定于1,符合驰振小频率的特点。
2.3 尾涡模式
关于尾涡模式的定义最早由Williamson 和Roshko[23]给出,包括2S、2P 和2C 等,S 表示单个旋涡,P 表示一对旋转方向相反的旋涡,C 表示一对旋转方向相同的旋涡。 研究表明尾涡模式主要取决于雷诺数,如图10(a)-(f)为c*=0.02 时不同雷诺数下的尾涡流态图,其中红色和蓝色表示旋涡方向相反。
随着雷诺数的增大,图10(a)所示的2S 模式逐步过渡为如图10(f)所示的2P 模式,尾涡被逐渐拉长,旋涡脱落距离圆柱尾部越远,拉长的旋涡具有更多的能量,因而可以激发圆柱振子更大的振幅。
取c*=0.02,U*=13.37,对应的Re =124 460,这时已处于驰振区,对一个周期内的各个时刻尾涡流态图进行研究。图11(a)-(g)为同一周期内不同时刻的尾涡流态图。可以发现的是,一个周期内圆柱尾部共有两对相反的旋涡脱落,属于2P 型,但与传统2P 型不同的是,在上侧脱落的旋涡对大小基本相等,如图11(d)黑色线框所示,而下侧脱落的旋涡对大小不等,如11(b)黑色线框所示。

图10 c*=0.02 的尾涡形态Fig.10 Wake vortex (c*=0.02)

图11 c*=0.02 的驰振区尾涡形态Fig.11 Wake vortex of galloping (c*=0.02)
2.4 功率计算
利用前文给出的功率计算公式得出功率, 进而画出曲线, 图12 所示为c*=0.14 的功率曲线。 c*=0.02 时,所得功率用于系统阻尼耗散,并不能得出输出功率,所以未画出。
由图可看出,同对称粗糙带圆柱相比,非对称粗糙带圆柱流致振动在上分支有更大的输出功率,在驰振分支则结论相反。对称粗糙带c*=0.14 时,非对称粗糙带单圆柱最大输出功率为6.62 W,实验所得最大功率为7.29 W。 除上部分支外,趋势吻合良好,由前文所给计算公式及第2.2 节频率响应可看出上分支区吻合不好主要可归因于频率捕捉的不准确。
3 结 论
本文利用ANSYS-Fluent 软件模拟非对称粗糙带单圆柱流致振动现象, 结合UDF 功能和动网格技术来控制非对称粗糙带圆柱的振动,研究讨论了不同阻尼下的振幅、频率、尾涡模式和功率输出等,并与实验结果进行对比。 得出的结论主要有:
(1) 非对称粗糙带单圆柱流致振动正负向振幅值不同,粗糙带侧位移值较小。
(2) 非对称粗糙带振幅比曲线捕捉到了初始分支区、上分支、上分支-驰振过渡分支和驰振分支,但数值计算捕捉上分支不明显。
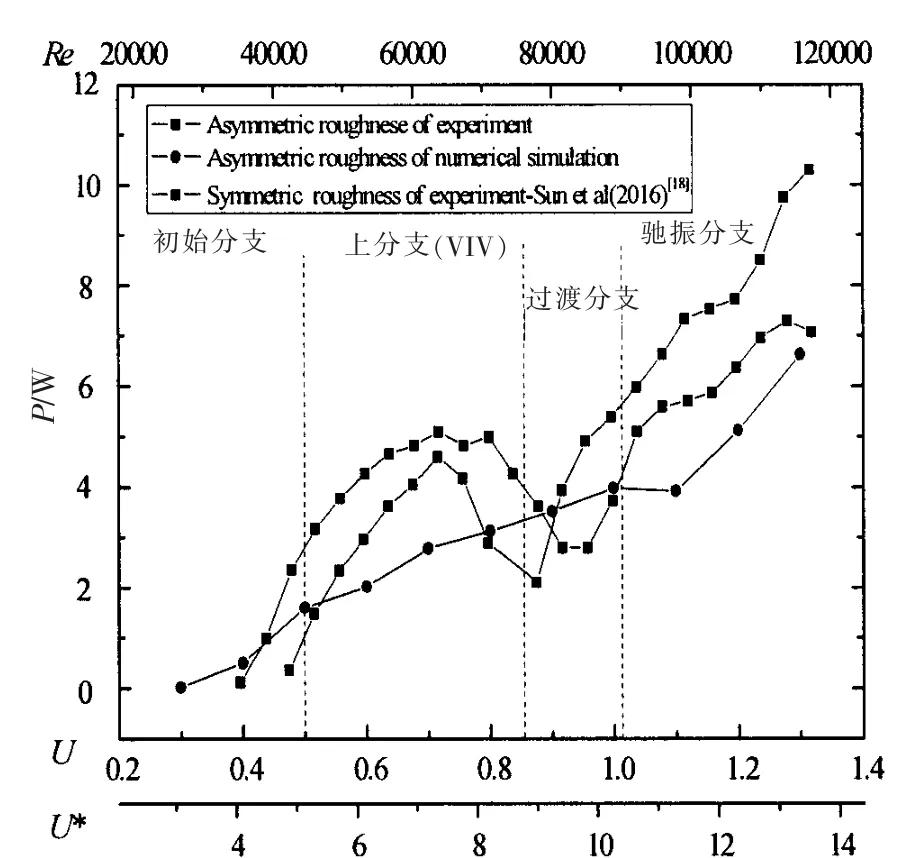
图12 c*=0.14 的功率曲线Fig.12 Power curve (c*=0.14)
(3) 相对于光滑圆柱,非对称粗糙带对上分支有明显的拓宽作用。
(4) 与光滑圆柱不同,非对称粗糙带单圆柱流致振动在进入驰振分支后,频率比下降并稳定于某一值,本文实验为1.1,数值计算为1。
(5) 在所研究范围内,随着雷诺数的增大,非对称粗糙带单圆柱的尾涡被逐渐拉长,旋涡脱落距离圆柱尾部越远,模式从2S 过渡为非对称的2P。
(6) 同对称粗糙带圆柱相比,非对称粗糙带圆柱流致振动在上分支有更大的输出功率,驰振区则相反。
(7) 本文通过数值计算得到的非对称粗糙带单圆柱最大输出功率为6.62 W,实验所得最大输出功率为7.29 W。
