南水北调台儿庄泵站扬压力安全监控指标拟定

2019-11-09张运保吕晓理郭晓翠

水利技术监督 2019年5期

张运保，吕晓理，郭晓翠

(南水北调东线山东干线有限责任公司，山东济南 250109)

1 台儿庄泵站概况

台儿庄泵站是南水北调东线一期工程的第七级泵站，主要任务是抽引骆马湖来水通过韩庄运河向北输送进入南四湖，以完成南水北调东线工程向北及胶东调水的任务，实现梯级调水目标。台儿庄泵站设计调水流量125m3/s，设计站上水位25.09m、站下水位20.56m，设计扬程4.53m，平均扬程3.73m；站下最高水位为22.50m，站上最高水位为25.50m。台儿庄泵站为I等工程，主要建筑物为1级，次要建筑物为3级。

2 研究方法

安全监控指标是评估和监测建筑物安全的重要指标。估计安全监控指标的主要任务是根据建筑物已经抵御经历荷载的能力，来评估和预测抵御可能发生荷载的能力，从而确定在该荷载组合下监控效应量的警戒值。但是，有些建筑物可能没有遭遇最不利工况；另外，建筑物抵御荷载的能力在变化。因此，在实际工程中，拟定安全监控指标是一个相当复杂的问题，需要根据建筑物的具体情况，用多种方法进行分析论证。本次研究采用置信区间法和典型监测效应量的小概率法进行台儿庄泵站扬压力安全监控指标的拟定。

3 台儿庄泵站扬压力监测资料分析

台儿庄泵站在主厂房底板、副厂房和安装间基础、进出水池和进出水渠共布设渗压计15支，本次对7#、11#、13#、21#渗压计进行分析，分析时段为2012年11月5日至2018年8月20日。以下基于原始观测资料，对监测数据的特征值以及时空变化规律进行重点分析，确定各效应量与环境量变化之间的相关性。

3.1 特征值分析

特征值统计以及过程线所使用的数据均将扬压力换算成扬压水位，各测点特征值统计见表1。

3.2 时空规律分析

由图1至图4可以看出扬压水位受河道运行水位的影响比较大，当河道水位升高时，扬压水位增大；当河道水位降低时，扬压水位减小。此外，相较于河道水位，各处扬压水位有一定的滞后效应，即其变化滞后于河道水位，而且距离河道越远，滞后效应越明显。

图1 台儿庄泵站7#渗压计水位过程线

表1 台儿庄泵站渗压计特征值统计表

图2 台儿庄泵站11#渗压计水位过程线

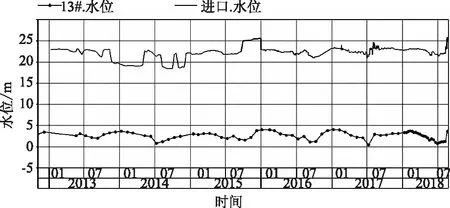
图3 台儿庄泵站13#渗压计水位过程线

图4 台儿庄泵站21#渗压计水位过程线

4 扬压力安全监控指标拟定

4.1 置信区间法

4.1.1监控模型及因子选择

考虑到泵站扬压力主要受河道水位、时效等因素变化的综合影响，其监控模型基本关系式表示为：

H=Hh+Hθ

(1)

式中，H—扬压力；Hh—水位分量；Hθ—时效分量。

(1)水位分量。河道水位变化对泵站扬压力有一定的影响，且有一定的滞后性，因此考虑选择监测日当天水位，以及前7天和前14天的平均水位作为因子，水位分量可以表示为：

(2)

式中，a1i—河道水位分量的回归系数(i=1～3)；hui—分别为监测日当天、监测日前第7天、前第14天的河道平均水位；hu0i—初始监测日上述各时段对应的河道水位平均值(i=1～3)。

(2)时效分量。考虑到泵站受多种因素的复杂作用，通常认为正常运行的泵站，时效分量变化的规律为初期变化急剧，后期渐趋稳定。时效因子通常选为θ和lnθ(θ为观测日减去基准日的天数)，因此应力的时效分量可表达为：

表2 泵站渗压计的回归模型

Hθ=b1θ+b2lnθ

(3)

4.1.2模型创建

经过计算各影响量之间基本无相关性，所以采用逐步回归分析方法计算统计模型参数，建模时段为2013年5月21日至2018年8月25日，分析时段的起始时间为仪器开始测量的时间。监控模型表示为：

(4)

4.1.3模型分析

表2为泵站各支渗压计统计模型的复相关系数R、剩余标准差S、分量分解百分比和回归模型方程式。从表2可以看出，5支渗压计中仅测点21#的复相关系数达0.74，表明实测数据的建模效果较好；其余4个测点的复相关系数均小于0.5，普遍较低，表明模型回归效果较差。

4.1.4监控指标估算

经前述分析可知，7#、11#、13#和15#测点的模型拟合精度较低，已严重失真，无法用于监控指标的拟定。仅21#测点建立的回归模型质量良好，因此可将21#测点的模型成果代入以下公式得到扬压水位的监控指标：

(5)

式中，Hm—监控指标；H—模型计算极值；S—剩余标准差；K—显著性水平α的函数。

K的取值和显著性水平α有关，通常将1-α称为置信水平，标志实测值落在监控指标范围内的概率。根据工程经验，一般取K=2，此时置信水平为95.4%。

模型计算极值的确定首先需求出最不利荷载组合，这是一个比较复杂的问题。本次分析采用“可能的最不利荷载组合”推求极值，考虑到扬压力主要受水位影响，且与水位呈正相关，因此选取水位达到最高时作为最不利时刻，实际计算时选取26.51m为出水池最高水位。基于模型方程和剩余标准差，估算出测点21#监控指标为22.54m，如图5所示。