偏联系数的计算与应用研究

杨红梅，赵克勤

（1. 山西广播电视大学 成人教育学院，山西 太原 030027; 2. 诸暨市联系数学研究所，浙江 诸暨 311800）

联系数是赵克勤在集对分析理论中给出的一种新颖结构函数，具有“数与系统合一”特点。借助联系数进行数学建模，结合系统的不确定性分析，使集对分析在处理不确定性问题中得到广泛应用[1-41]。偏联系数是联系数的一种伴随函数，也是基于集对分析的“系统状态-趋势分析法”的主要数学工具，自赵克勤于2005年提出以来[42]，已在飞机维修[43]、地铁施工[44]、隧道施工[45]、矿山过程安全[32]、火灾预防[46]、水文水资源[47]、区域创新[48]、技术预警[49]、教育评估[50]、网络舆情传播[51]、建筑供应链风险管理[52]、卫生统计[53]、系统风险分析[54]、隐私保护[55]等领域得到应用。最近，文献[56]建立一种融合偏联系数模糊聚类(PCFCM)算法和教与学随机森林(TLRF)算法的雷达调制信号分选新模型(PCFCM-TLRF)，仿真实验结果显示，与其他分选模型相比，PCFCM-TLRF模型具有更高的分选准确度，能够有效地实现雷达调制信号的分选。

但由于文献[42]所在出版物不是学术期刊，传播上有一定局限，致使相当一部分应用偏联系数的学者看不到文献[42]。为此，本文对偏联系数的计算与应用研究作一梳理，以促进集对分析和偏联系数在人工智能等领域中的进一步应用。

1 联系数及其联系分量的示性系数

由文献[19]知，联系数最早由赵克勤在解读集合论罗素悖论时给出，至今已有不同的表达形式，其中常用的二元到五元归一化联系数为

但式(5)给出的是式(1)～(4)中联系分量示性系数i、j、k在[-1，1]大区间取值作均匀分布假定条件下的值域，这些在给定小区间中取何值仍要根据联系分量本身的不同情况才能确定，这是联系数的一个重要特点，也是对联系数开展系统分析的一个难点，如何消去这些不确定取值的示性系数，得出联系数系统在微观层次上的演化趋势，已成为集对分析理论研究中的一个热点，后面要讨论的偏联系数算法就是针对这一难点作出的探索。

2 偏联系数

2.1 基本原理

偏联系数主要依据联系数的假定提出：假定联系数中当前处在较低(负、偏负、正负不定)层次和较高(正、偏正)层次的联系分量存在由低(负、偏负、正负不定)到高(正、偏正)的正向层次迁移，同时又存在由高(正、偏正)到低(负、偏负、正负不定)的负向层次迁移，这些联系分量之间相互对立的层次及其迁移构成联系数的系统结构(由联系分量组成的结构)在微观层次上的矛盾运动，运动结果决定这个联系数的系统结构在微观层次上的演化趋势，该演化趋势与同一联系数的联系分量在宏观层次上的演化态势可能相同，可能相异，可能相反。

显然，以上假定符合哲学关于事物处于运动和变化之中的思想，也是不少文献中的实例验证，因此也称为联系数中联系分量的微观运动原理或矛盾运动原理，不致误解时，简称联系数微观运动原理。研究表明，联系数的微观运动原理就是偏联系数原理。

2.2 二元联系数的偏联系数

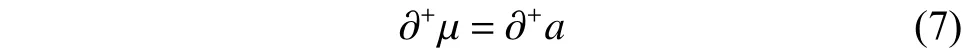
也就是：

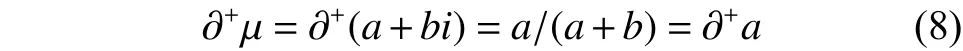
因此有定义1：

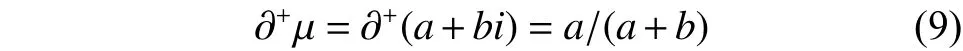
另一方面，根据集对分析的“成对原理”(事物或概念都是成对存在)和联系数中联系分量的微观运动原理，可以假定当前的原本也处在层次，是从层次朝正负不定(相对于完全确定的+1层偏负)演化而来，为此用作分母，用作分子，用作为演化率，记

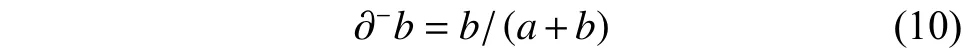
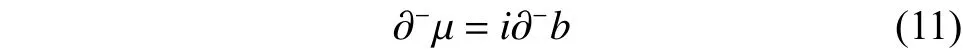
也就是：

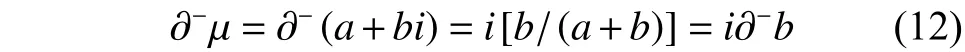
因此有定义2：

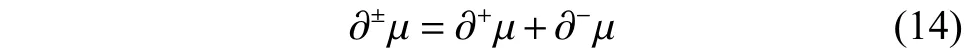
根据定义3可知：

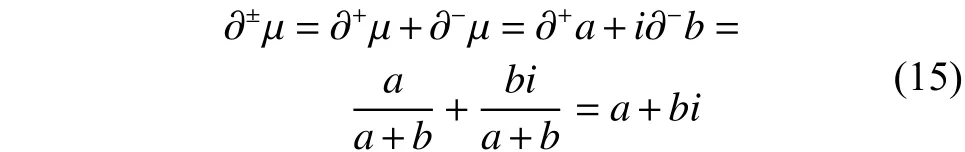
式(15)表明二元联系数的一阶全偏联系数是二元联系数自身，计算结果中仍然存在二元联系数中表示不确定性的示性系数 i，为此，在实际应用时需要对 i 作出解析才能确定二元联系数所确定的演化趋势。

2.3 三元联系数的偏联系数

式(2)所示三元联系数的偏联系数计算原理同二元联系数，但内容较多；为节约篇幅，以下直接给出三元联系数中各阶偏联系数的定义(见定义4)。

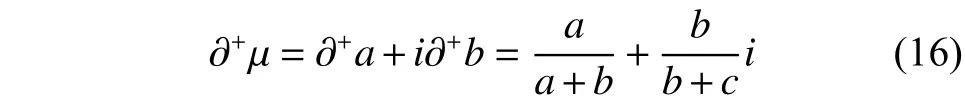
三元联系数的一阶偏负联系数见定义5。

式(17)表明三元联系数的一阶偏负联系数是一个二元联系数，由两个偏负联系数相加而成，其中的含义是假定当前的，此前也处在b层次，是从b层次负向演化而来，所以用做分子，用偏负向演化的演化率，由于这时作为分子的处在当前状态，所以乘上表示当前状态的示性系数。

三元联系数的一阶全偏联系数见定义6：

则其一阶全偏联系数是一阶偏正联系数和一阶偏负联系数的代数和，记一阶全偏联系数为，则有

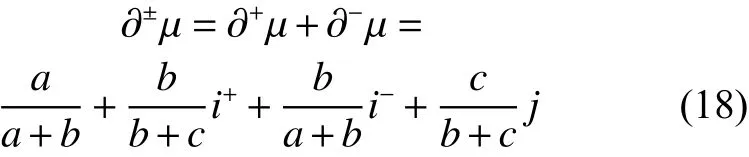
显然，定义6中的式(18)可以化简成：

如果约定三元联系数的偏联系数就是指这个三元联系数的全偏联系数，则式(19)可以再简写成：

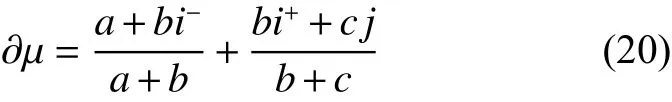
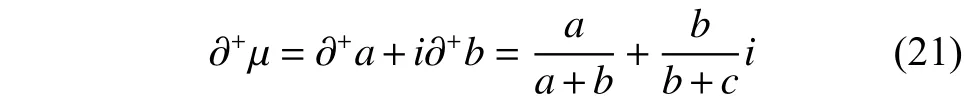
进一步有定义9。

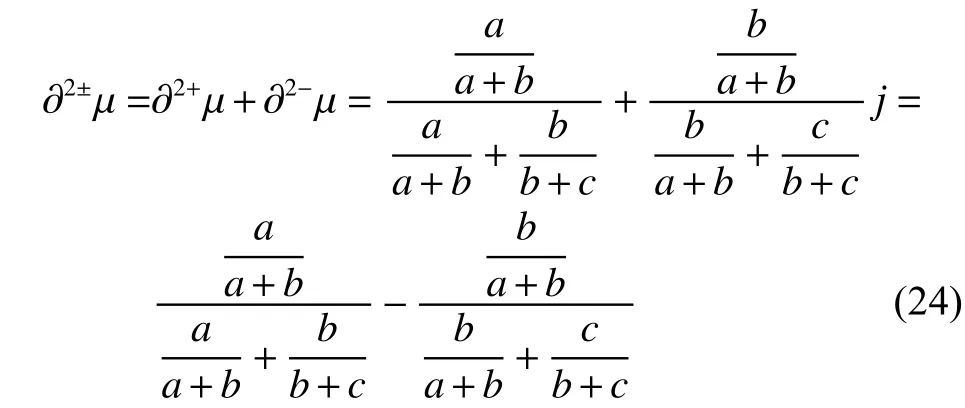
显然，式(24)是一个没有示性系数 i 的实数，其物理意义是：当时，表明三元联系数的系统在微观层次上的演化趋势是正向趋势；当时，表明三元联系数的系统在微观层次上的演化趋势是负向趋势；当时，表明三元联系数的系统在微观层次上的演化趋势处在正负临界状态。

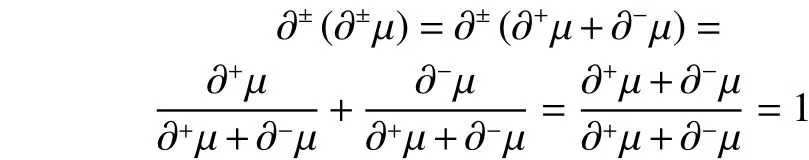
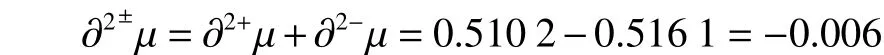
2.4 四元联系数的偏联系数

式(3)所示四元联系数的偏联系数计算原理同三元联系数，但内容增多；为节约篇幅，以下直接给出四元联系数中各阶偏联系数的定义：

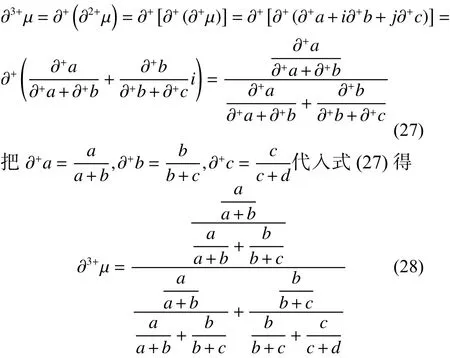
显然，式(33)是一个没有示性系数 i 的实数，其物理意义是：当时，表明四元联系数的系统在微观层次上的演化趋势是正向趋势；当时，表明四元联系数的系统在微观层次上的演化趋势是负向趋势；当时，表明四元联系数的系统在微观层次上的演化趋势处在正负临界状态。

2.5 五元联系数的偏联系数

式(4)所示五元联系数的偏联系数计算原理同四元联系数，但内容增多；为节约篇幅，以下直接给出五元联系数中各阶偏联系数的定义(见定义9)：

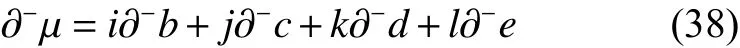
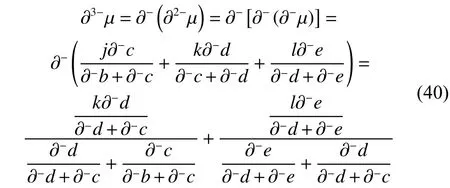
3 反偏联系数

4 偏联系数算法研究的若干新思路

4.1 加权偏联系数

北京师范大学研究生易测吉在2018年第6期全国偏联系数专题高级讲研班上提出，联系数中不同层次的联系分量之间的层次迁移，也可能存在一个联系分量在一次层次迁移中，只有其中的一部分参与层次迁移的情况。经我们研究，基于易测吉思路形成的偏联系数算法与第3章所定义的偏联系数算法有不同，由这种新算法得到的偏联系数是否可以称为加权偏联系数，待进一步研究。

4.2 基于相互作用的全偏联系数

赵克勤在2018年第6期全国偏联系数专题高级讲研班上还讲到联系数中相邻联系分量以乘积形式表示的相互作用联系数，基此情况，给定一个元联系数，可以衍生出个元联系数；元联系数的阶全偏联系数，显然是元联系数的阶全偏联系数的细化，但其计算过程也较复杂，需要进一步研究。

最近，金菊良等[58]又提出效应全偏联系数，并把其用于水资源评价，也需进一步研究。

5 应用举例

例3 随机抽取某广播电视大学2016级行政管理专业30名学生7门课程成绩(见表1)，试用偏联系数计算这7门成绩的提高趋势，其中为应用写作，为英语，为管理学基础，为中国特色社会主义理论，为开放教育入学指南，为西方行政制度，为地域文化。

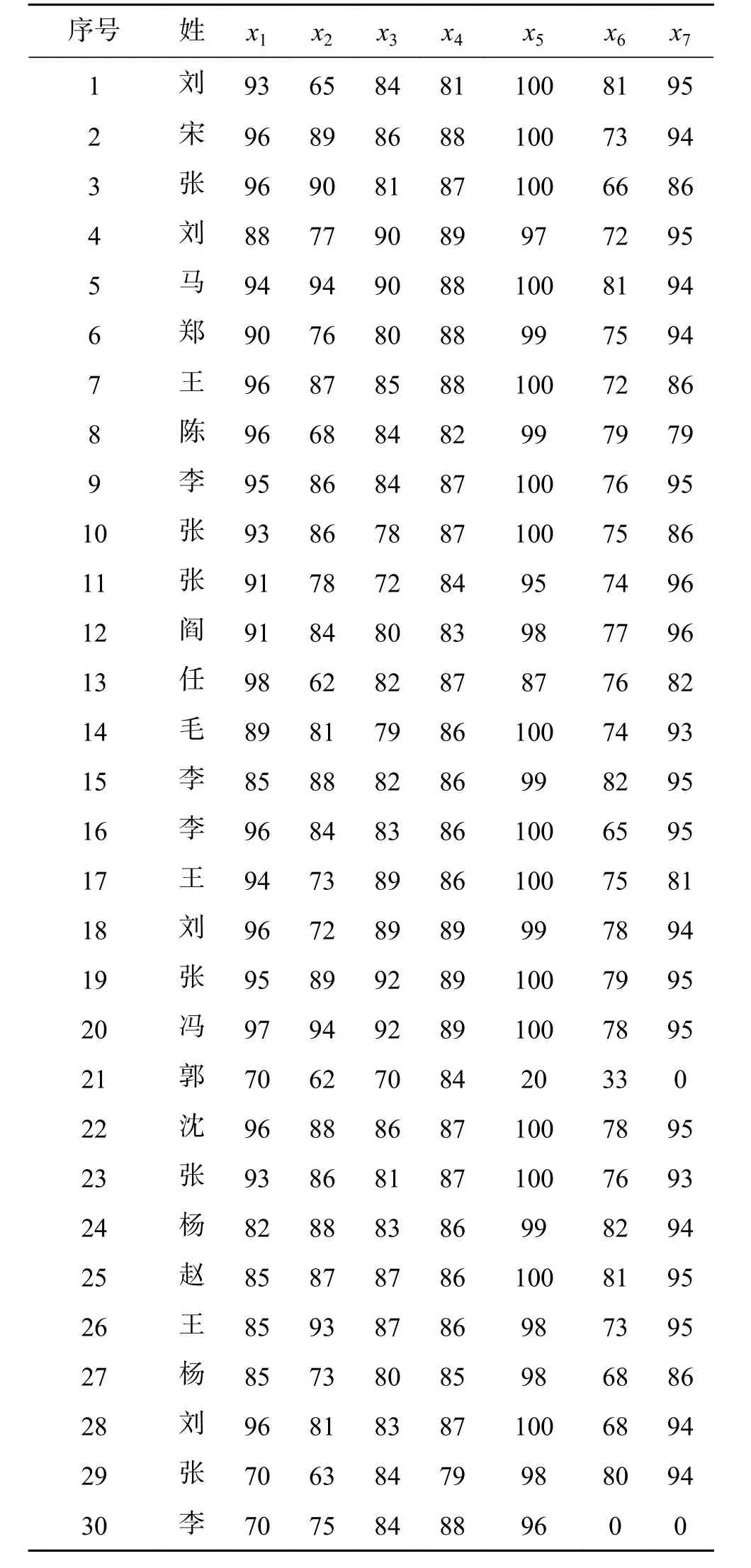
表1 30位学员x1～x7课程成绩Table 1 30 students' x1～x7 course results

2)把上述五元联系数归一化处理，得：

3)按式(42)计算全偏联系数，并对全偏联系数的大小作出排序，得

6 讨论

1)关于事物微观运动的数学刻画。众所周知，客观事物处于相互联系和运动变化之中，如何定量刻画事物的相互联系和运动变化，是包括人工智能学者在内的众多科技人员的研究课题。文献[1-60]和本文的工作表明，基于集对分析理论的联系数及其偏联系数是定量刻画事物相互联系和运动的一个新数学工具，其理由：首先，偏联系数把联系数中的各个联系分量不再看作相互独立的量，而是假设成一定条件下相互生成的量，理论上，这种假设成立；其次，借助偏联系数的算法，揭示联系数中联系分量的相互生成是在微观层次上的一对矛盾运动，这也可以接受；因为哲学、物理学和无数事实告诉我们，矛盾普遍存在，运动成对进行，“作用力与反作用力大小相等，方向相反，作用在2个不同的物体上”已是一种科学常识；再次，偏联系数着眼于事物的运动在微观层次上的定量刻画。科学史表明，牛顿的微积分在刻画事物宏观层次上的运动已取得巨大成功,但人们对事物在微观层次上的运动观测和测量则受制于海森堡的“测不准原理”；正是在这一点上，集对分析借助联系数对不确定性“客观承认、系统描述、定量刻画、具体分析”[59]，使得基于联系数的偏联系数算法能够刻画出事物在微观层次上的矛盾运动。当然，微观与宏观是一个相对的划分，文献[19]中指出，“在生物学中，全体是宏观，个体就是微观；个体是宏观，细胞就是微观；细胞是宏观，基因就是微观；在物理化学中，肉眼直接见到的是宏观，要在显微镜下看到的是微观；在低倍显微镜下看到的是宏观，在高倍显微镜下看到的是微观；在时间序列中，世纪是宏观，年度就是微观；年度是宏观，月度是微观，小时是宏观，分钟就是微观；分钟是宏观，秒是微观，如此等等”。

正是宏观与微观划分的相对性，导致事物在宏观层次上相对静止的同时，在微观层次上依然发生着细微尺度上的变化和运动，如实刻画事物宏观状态的联系数因而能借助偏联系数的计算刻画事物在微观层次上的运动规律。

3)关于偏联系数的生成机制和时态。在偏联系数计算过程中，需要注意各阶偏联系数中各联系分量的生成机制和时态。一般地说，用分式表示的某阶偏正(负)联系数中的联系分量，其分子的状态指过程完成时所处的状态，分母的状态则是过去进行时的状态，例如三元联系数，其一阶偏正联系数为

用同样的道理可以合理地处置例3中五元联系数的偏联系数计算过程中遇到的“”如何运算的问题，例如，按式(34)，其一阶偏正联系数为学中被认为是一个无意义的式子(零不能作除数)，在高等数学中被认为是一个不确定式，但按前面的讨论可知，分子是代表的，这个是当前状态的，是确定的；分母中代表的也是确定的，分母中代表的虽然与代表的处在同一个层次，却是一个在变化着的，按微积分思想，这个在变化着的0，本质上是一个以零为极限的无穷小量，由此可知分母实质上是。这一结果从问题本身的角度也说得通，因为说明当前状态下，确实没有出现60～70分之间的成绩。同理，可以处置在计算

4)不难推知，第4章中有关加权偏联系数和效应全偏联系数的算法，以及基于相互作用的偏联系数算法，要比第2章中介绍的偏联系数基本算法复杂，由此推知反加权偏联系数、反效应全偏联系数、反相互作用偏联系数的算法更复杂，限于篇幅，本文没有展开介绍，特此说明。

5)偏联系数算法是一种新的智能算法。首先，从信息利用的角度看，偏联系数算法有效地挖掘了联系数中联系分量的动态信息，这种动态信息反映出联系数所刻画的研究对象的本质。因为客观事物总是处于动态变化之中，某一时刻相对静止的宏观状态与这种状态在微观层次上的变化趋势共存在一个系统中是所有研究对象的共同属性，借助联系数的偏联系数计算，能够看到系统在宏观静态下的微观动态，显然是一种智能；其次，从系统的角度看，偏联系数算法揭示了对象系统线性与非线性的关系，因为从形式上看，联系数中的各个联系分量可以有序地放置在一根水平轴上，具有明显的线性特征，但式(6)～式(42)表明，偏联系数所展示的图象是一幅非线性图象；再次，从人工智能技术创新的角度看，基于偏联系数的聚类、模式识别、系统综合评价决策与风险防控以及社交网络中的隐私保护研究，也在一定意义上属于智能技术的范畴，偏联系数算法因而是一种新的智能算法，需要作深入系统研究。

6)运动需要能量，无论这种运动处在宏观层次还是微观层次。偏联系数及其算法既然刻画了联系数中联系分量之间的矛盾运动，人们自然会问，驱使这种运动的能量又是什么性质的能量？回答是“信息能”。“信息能”是赵克勤在2015年7月在杭州举办的第3期非传统安全集对分析研学班上提出的一个概念，认为信息是物质和能量相互作用的产物，信息具有能量，称为信息能[15,60]。联系数是刻画研究对象某个特定状态的一个信息系统，本身蕴含着一定的信息能，且具体蕴含在联系数中联系分量所在不同层次的系统结构中；偏联系数及其算法在一定程度上开发了这种“信息能”，得到的结果让人们从系统的一组宏观状态参数中认识和掌握这种状态在微观层次上的演化趋势，从而把联系数中的“信息能”在一定程度上转化成“智能”；但更多关于“信息能”转化成“智能”的问题待深入研究。

7 结束语

联系数是一种结构函数，也是集对的特征函数，具有系统和数的双重特性。偏联系数是联系数的一种伴随函数，其计算过程和计算结果刻画了联系数中全体联系分量在微观层次上的相互联系、相互制约和相互生成的矛盾运动，具有丰富的系统信息。本文从应用的角度梳理了二元到五元联系数的偏联系数计算，指出规范地计算一个联系数的偏联系数是得出正确结果的一个前提，文中给出的算法可以推广到元联系数的偏联系数计算。此外，也简要地介绍了近期有关偏联系数的若干创新思路和创新算法。

数学是人工智能的基础。偏联系数是一个新的数学概念，由于人工智能面临的实际问题众多，偏联系数计算又是一种新的信息处理算法，因而有许多问题需要作进一步的系统深入研究。