一种对称残差CNN的图像超分辨率重建方法
2019-11-08刘树东王晓敏
刘树东,王晓敏,张 艳
(天津城建大学 计算机与信息工程学院,天津 300384)
图像超分辨率(Super-Resolution,SR)重建是图像复原中的一个重要分支[1],是一种由低分辨率图像恢复对应高分辨率图像的方法。随着图像超分辨率在卫星成像[2]、医学成像[3]、安全和监视[4]、图像生成[5]等计算机视觉任务和图像处理领域取得的突出成就,利用超分辨率技术重建出更高分辨率、更清晰的图像成为目前图像复原领域的研究热点。
图像超分辨率重建最早是由文献[6]在20世纪60年代提出的。随着超分辨率技术的广泛应用,越来越多的学者开始对其进行探究。图像超分辨率重建方法主要有3种:基于插值的方法[7]、基于重建的方法[8]和基于学习的方法[9-10]。基于差值的超分辨率重建方法计算简单,容易实现,但对自然图像的先验知识具有较大的依赖性,对图像细节恢复效果较差,容易出现边缘效应。基于重建的方法根据已知的退化模型得到低分辨率图像,通过提取低分辨率图像中关键的像素点信息对高分辨率图像的生成进行约束,结合高分辨率图像中的先验知识得到相应的重建结果。但由于获得的先验知识有限,因此对于复杂的图像无法恢复出更多细节信息,重建性能有限。基于学习的方法通过建立高、低分辨率图像两者之间的映射关系,然后利用学习获得的先验知识来完成高分辨率图像的重建。与其他重建方法相比,基于学习的图像超分辨率方法可以从训练样本中学习到所需的细节信息,并对测试样本进行估计,可获得相对较好的重建效果。目前基于学习的方法主要有基于稀疏表示、近邻嵌入和深度学习的方法。文献[11-12]提出一种基于稀疏表示和字典学习的方法,通过学习低分辨率图像块和对应高分辨率图像块的超完备字典进行图像重建。但由于对超完备字典的学习要求较高,实用性较差,文献[13-14]将稀疏字典和领域嵌入进行结合,提出了锚定领域回归算法和改进后的锚定领域回归(A+)算法,计算效率得到了提高,但图像细节恢复效果较差。
随着深度学习的飞速发展,基于深度学习的方法与传统方法[15-16]相比有显著的优势。卷积神经网络(Convolutional Neural Network,CNN)作为深度学习的代表性算法之一,由于其高效的学习能力,在超分辨率领域得到了广泛的应用[17-18]。文献[9]采用3层卷积神经网络(Super-Resolution Convolutional Neural Network,SRCNN)进行图像超分辨率重建。该网络结构简单,容易实现,但由于卷积层数少、感受野小以及泛化能力差等缺陷,无法提取到图像深层次的特征,导致重建性能有限。文献[19]提出的卷积网络将网络深度提升到了20层,并引入了残差学习,提高了特征提取能力。同时,文献[20]还提出了深度递归卷积网络,采用递归学习实现了深度网络的参数共享,降低网络的训练难度。虽然文献[19-20]提出的两种方法取得了较好的重建性能,但是随着网络的加深,梯度消失和网络退化也会越明显。文献[21]提出了深度拉普拉斯金字塔网络,采用级联结构逐步学习,逐步优化,取得了很好的重建效果。文献[22]提出了一种深度残差递归网络,通过循环残差的方式减少训练参数,降低网络训练难度,有效缓解了梯度消失现象。文献[23]提出的深度残差编码解码网络,采用对称方式跳跃连接卷积与反卷积层,使训练收敛速度更快,达到更高质量的局部最优,但随着网络深度的增加,梯度消失或网络退化现象仍然存在。
笔者针对上述方法的不足,将对称跳跃连接引入到卷积神经网络,提出了一种基于对称残差的卷积神经网络模型,以进一步提高图像重建的质量。通过在残差块内建立对称短跳连接,实现块内信息充分利用,提取更丰富的局部特征,同时,在残差块外建立长跳连接,实现全局特征融合,以弥补深度网络图像细节信息退化严重的损失。针对损失函数的选择,采用处理异常点更稳定的平均绝对值误差(Mean Absolute Error,MAE)函数进行训练。
1 相关工作
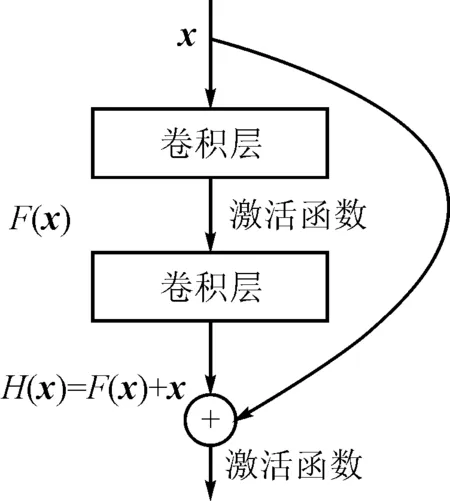
图1 残差结构图
文献[23]提出的深度残差编码解码网络是一种对称网络结构,将卷积神经网络中的卷积和反卷积操作运用于图像复原。首先,对称跳跃连接有助于图像信息直接反向传播,从而缓解了梯度消失的现象,使深度网络训练更加容易,提高了网络的恢复性能。随着卷积神经网络深度的增加,残差网络中的残差结构可以有效缓解深度网络引起的梯度消失和网络退化现象,网络架构越深,其丰富抽象特征的提取和网络性能越好。
文献[24]提出的152层深度残差网络(Residual Network,ResNet)利用非线性网络可以拟合任意函数的特性,使用包含少数隐层的浅层网络拟合自定义的残差函数F(x):=H(x)-x,残差函数再与恒等映射x相加,x表示网语的输入,构成基本的残差单元,实现期望的特征映射关系H(x)[25]。研究表明,这种方式更易于优化[6,26-30]。如图1所示,残差结构在解决梯度消失问题的同时,避免了因网络加深而导致的额外参数引入,在深层网络中使用跳跃连接的方式将卷积层连接,实现了不同卷积层中特征的重复利用,大大降低了训练时的计算量[31]。文献[18]在输入数据和最后重建层之间采用跳跃连接进行信息传递。研究表明,在各层之间建立多个跳跃连接可以有效地训练深度网络[21]。
由于网络深度的不断增加,该方法将残差网络引入图像超分辨率以解决深度网络训练难度大的问题;将一种对称长短跳跃连接引入卷积神经网络,通过在网络中设置带泄漏线性整流(Leaky Recitified Linear Unit,LReLU)函数作为激活函数,使网络训练更稳定,并以原始低分辨率图像作为输入,减少图像经预处理后导致高频信息丢失的现象,进一步提高了网络的特征提取能力。
2 对称残差卷积神经网络模型
2.1 对称残差卷积网络结构
基于对称残差的卷积网络(Symmetric Residual Convolution Neural,SymRCN)模型主要由特征提取、特征融合和重建3部分构成,共包含31层卷积层。该网络模型包括4个残差块,采用对称长短跳跃连接实现全局与局部特征融合,实现网络训练的稳定性和特征提取的高效性。在残差块内采用对称残差的方式提取更丰富的特征,残差块外通过长跳连接实现全局特征融合,有效缓解了由简单堆叠多个残差块而导致特征提取不充分、梯度消失和网络退化问题。网络结构如图2所示,其中,x和y分别表示网络的输入和输出。
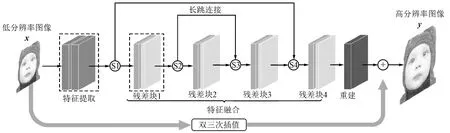
图2 对称残差卷积网络结构图
对称残差卷积神经网络模型建立时的具体实现步骤有3个:①特征提取。主要完成提取不同条件下的细节特征,将获得的低分辨率图像的稳定特征作为特征融合模块的输入数据;②特征融合。利用残差块内多个对称残差的卷积层和非线性映射函数的复合实现网络中不同特征图的提取;通过在残差块外建立长跳连接来完成各个残差块间特征的融合,并作为重建模块的输入数据;③重建。利用预测的残差图像重建出最终的高分辨率图像。
特征提取部分由两层卷积层构成,为了降低网络参数数量和计算复杂度,每层卷积层均使用64个大小为3×3的卷积核对原始低分辨率图像进行卷积,提取特征图。特征B0提取过程可以表示为
B0=f(x) ,
(1)
其中,f表示特征提取函数,x并作为下面残差块的输入。
特征融合部分由4个残差块组成,每个残差块由一个增强单元和一个压缩单元构成,这个过程可以表示为
Bm=Fm(Bm-1),m=1,2,…,n,
(2)
其中,Fm表示第m个残差块对应的函数,Bm-1和Bm分别表示第m个残差块的输入和输出。
重建部分使用一层无激活函数的反卷积层实现最终图像重建,该层的功能相当于上采样操作。在反卷积过程中,当步长s大于1时,反卷积操作被视为上采样,且网络的整体复杂度会降低s2,但步长不宜过大,因为过大的步长会导致重建质量的下降。根据采样因子的不同,相应调整步长大小,但步长始终大于1。重建过程中反卷积层对特征图进行上采样操作,将最终残差块的输出特征组合起来生成残差图像,其中,反卷积层的偏置项能够自动调整残差图像数据分布的中心值,使之接近原始图像。由于输入的原始低分辨率图像与高分辨率图像间存在极大的相似性,因而两者间残差图像的像素信息多数情况趋近于零。使用输入的低分辨率图像、原始高分辨率图像和生成的残差图像共同完成高分辨率图像的重建,进一步提高了图像的重建质量。网络的输出y可表示为
y=R(Fn(Bn-1))+U(x) ,
(3)
其中,R和U分别表示重建和双三次插值函数。
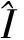
(4)
2.2 特征融合
特征融合是本网络的核心部分,由增强单元和压缩单元组成,Conv+LReLU(k,n)中k代表卷积核大小,n代表卷积核个数,并使用带泄漏线性整流函数作为激活函数。其中增强单元包含6层结构相同的卷积层,通过对称残差实现浅层与深层信息的恒等映射,融合网络上下文信息,提取更丰富的特征。压缩单元由1层1×1的卷积层构成,为后续网络提取关键信息。残差块内增强与压缩单元框架如图3所示。当前残差块的输出Bm-1可表示为
(5)
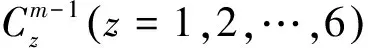
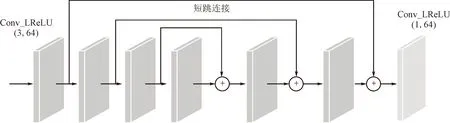
图3 残差块内增强与压缩单元框架图
3 实验结果分析
3.1 数据集预处理
使用文献[12]的91张图像和文献[32]中的200张图像作为训练样本。为了充分利用训练数据,通过对291张图像进行90°、180°、270°旋转,水平翻转,并以因子0.9、0.8、0.7、0.6的顺序缩小,对训练图像进行数据增强处理后获得训练图像11 640张。为了进一步证明提出方法的有效性,选择应用广泛的标准数据集Set5、Set14、BSD100进行测试,数据集中包含了丰富的自然场景,可以有效地测试网络的性能。
利用双三次插值法以因子k(k=2,3,4)对原始图像进行下采样,生成相应的低分辨率图像,将低分辨率训练图像裁剪为一组lsub×lsub的子图,相应的高分辨率训练图像被裁剪为klsub×klsub的子图。由于网络使用Caffe深度学习框架进行训练[33],所以将反卷积核产生的输出大小设置为(klsub-k+1)2,而非(klsub)2,因此,高分辨率子图的像素边界应裁剪(k-1)。同时,使用Caffe框架训练时,若拥有较大学习率的训练样本尺寸越大,则训练过程越不稳定。由于裁剪图像块时无重叠部分,为了充分利用291张图像,当采样因子增大时,子图像采样步长相应缩小,裁剪后的训练子图尺寸相应变小,以便得到更多边缘的图像块。以采样因子k=3为例,根据数据集中最小图像的尺寸,将低分辨率子图像采样步长设置为15,低分辨率图像裁剪为15×15(152)的训练子图,对应的高分辨率图像裁剪为43×43(432,其中高分辨率子图尺寸通过15×3-3+1获得)的训练子图,故训练阶段使用大小为152/432的训练对进行训练。初始学习率设为10-4,训练过程中,每250 000次学习率下降10-1,总的训练次数为600 000次。训练样本尺寸如表1所示。

表1 不同采样因子的训练子图尺寸
对于原始彩色图像,将每张彩色图像从RGB颜色空间转换为YCbCr彩色空间。由于人眼视觉相比于颜色对图像亮度更加敏感[34],在SRCNN中已经证明仅在Y通道进行映射关系不会影响图像的重建质量[9],所以仅对Y通道即亮度通道做训练从而得到对应的映射关系,对Cb、Cr颜色分量进行简单的插值放大,这样可以减轻计算的开销,同时保证了图像的重建质量[35]。
网络中,所有采样因子的上采样核均为17×17,带泄漏线性整流函数的负斜率设置为0.05,使用文献[36]提出的方法初始化权重,偏置设为零,网络使用Adam进行优化。
3.2 实验分析
实验硬件配置为Intel(R)Xeon(R)CPU E5-1650 v4 @3.60GHz×12处理器,Tesla K20c显卡,64GB内存,平台为Matlab R2016a软件和caffe深度学习框架以及用于调用GPU的开发包CUDA8.0。首先针对在残差块内使用和不使用对称短跳连接两种情况,采用两种不同的网络模型进行峰值信噪比(PSNR)的测试实验,然后使用标准测试集Set5、Set14、BSD100进行测试,将SymRCN方法与Bicubic、A+[13]、SRCNN[9]、VDSR[14]、DRCN[15]和LapSRN[16]6种典型方法的重建结果进行比较,使用峰值信噪比和结构相似度(SSIM)作为衡量图像重建质量的指标。
图4统计了残差块内是否使用对称,并经过600 000次迭代后,在Set5测试集上重建结果的平均峰值信噪比曲线图。从图4中可以看出,使用对称的网络模型,峰值信噪比值有明显提高,充分证明了使用对称可以有效改善网络加深带来的梯度消失现象。
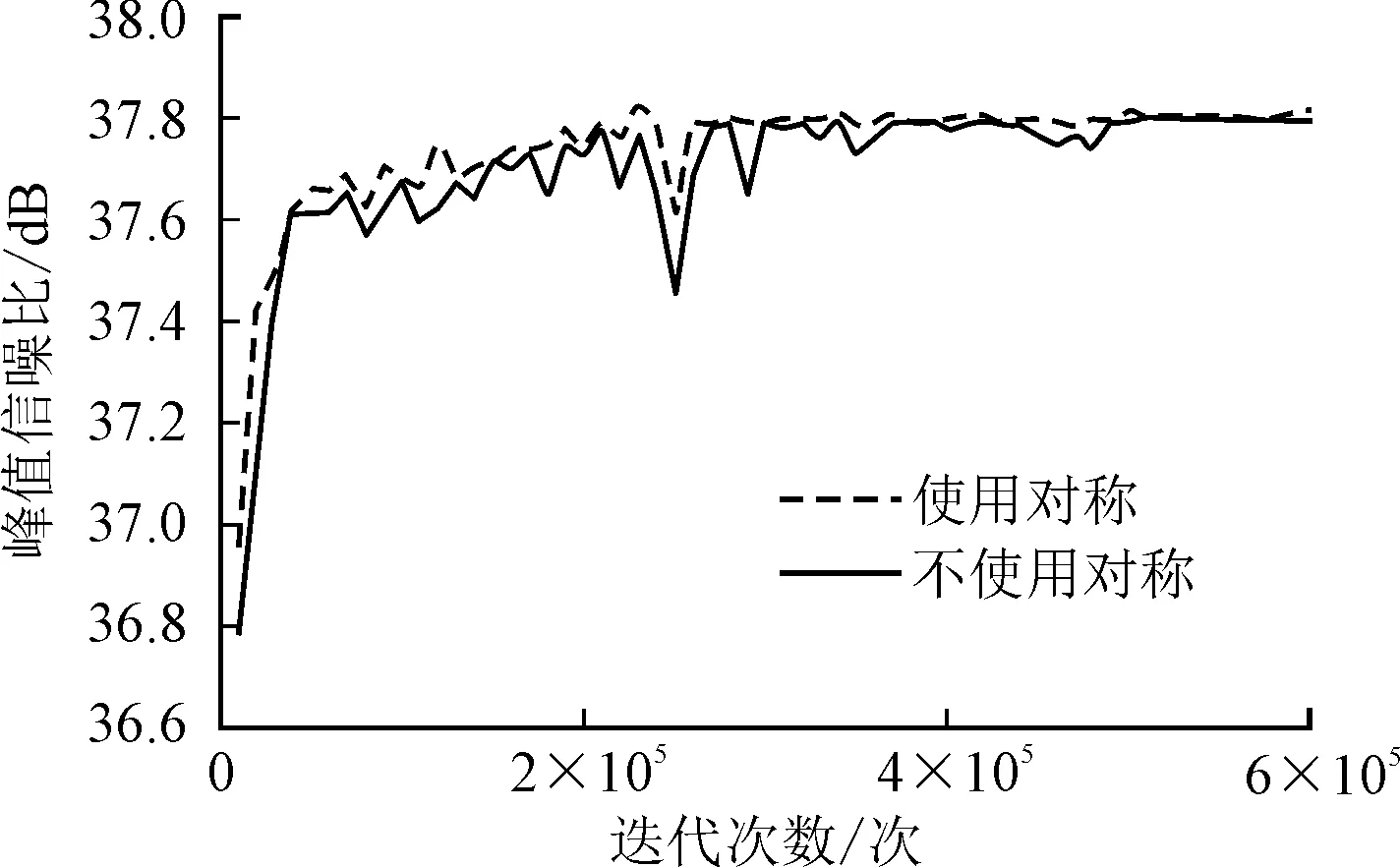
图4 在Set5测试集上两种方法的峰值信噪经收敛曲线
图5~图7展示了当采样因子为2倍、3倍和4倍时,在Set5和Set14测试集上使用对称残差卷积网络方法和其他6种方法进行重建后的图像对比,从主观角度对图像的重建效果进行了展示。可以看出,Bicubic和A+两种方法所重建的图像比较模糊,锯齿状较为明显,重建效果较差。SRCNN、VDSR、DRCN和LapSRN相较于前两种方法的重建效果较好,但重建图像仍然存在细节不完整,清晰度不够高的问题。在不同采样因子下,使用对称残差卷积网络方法重建Set5中butterfly_GT图像后的蝴蝶翅膀纹理更加清晰,细节更丰富,结构相似度更高;重建Set5数据集中的bird_GT图像后的小鸟身体各部位细节信息提取更充分,边缘更清晰,辨识度更高;重建Set14中zebra图像的峰值信噪比和结构相似度虽略低于LapSRN,但重建的图像与LapSRN算法重建的图像视觉感官上十分接近。同时,相较于其他5种方法,该方法重建图像更清晰,整体视觉效果更好。
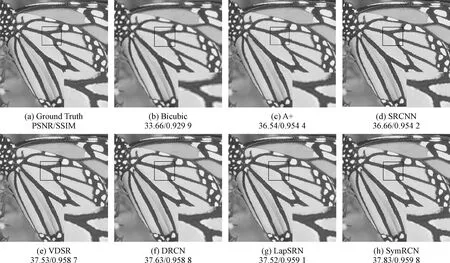
图5 Set5中的butterfly_GT采样2倍的重建对比图

图6 Set5中的bird_GT采样3倍的重建对比图
表2在Set5、Set14和BSD100数据集上不同超分辨率重建方法的平均PSNR/SSIM
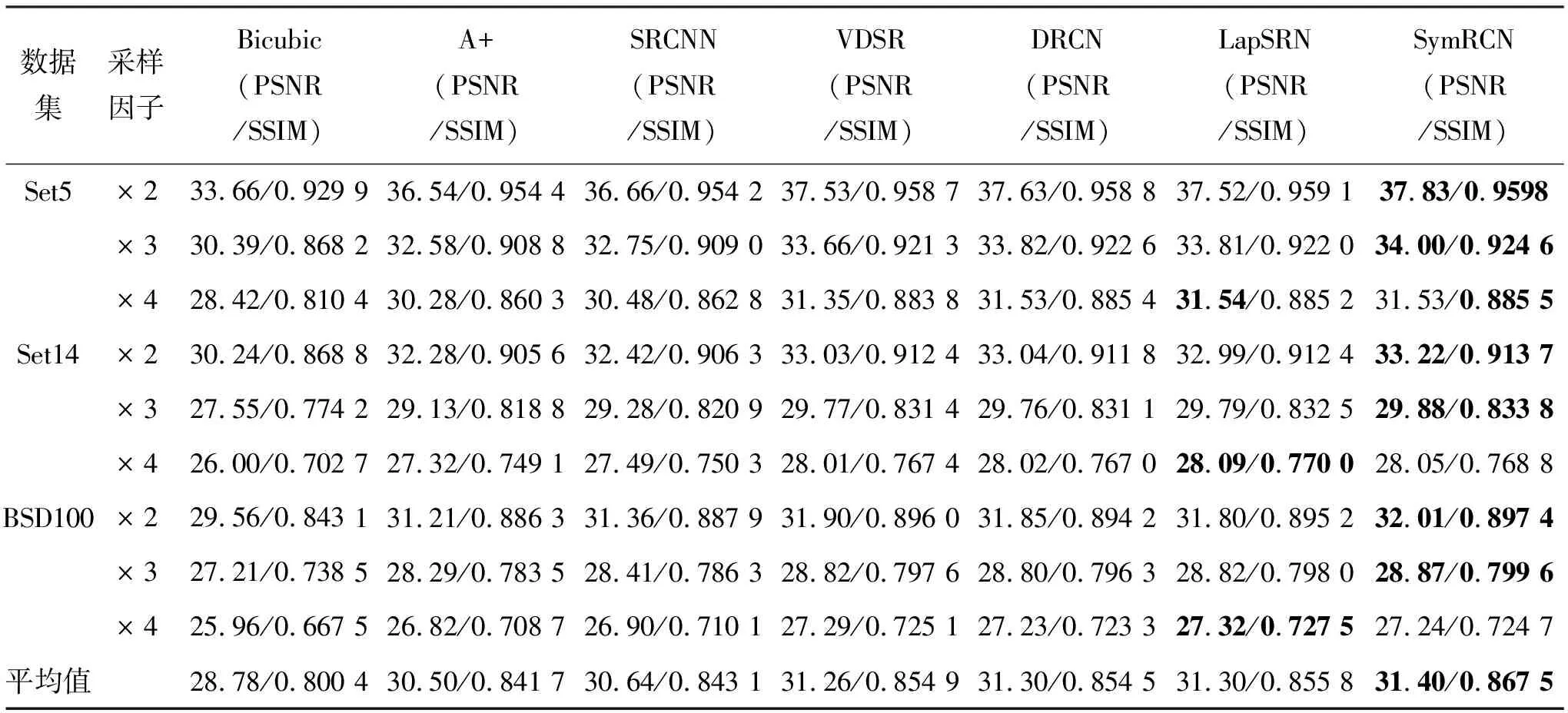
数据集采样因子Bicubic(PSNR/SSIM)A+(PSNR/SSIM)SRCNN(PSNR/SSIM)VDSR(PSNR/SSIM)DRCN(PSNR/SSIM)LapSRN(PSNR/SSIM)SymRCN(PSNR/SSIM)Set5×233.66/0.929 936.54/0.954 436.66/0.954 237.53/0.958 737.63/0.958 837.52/0.959 137.83/0.9598×330.39/0.868 232.58/0.908 832.75/0.909 033.66/0.921 333.82/0.922 633.81/0.922 034.00/0.924 6×428.42/0.810 430.28/0.860 330.48/0.862 831.35/0.883 831.53/0.885 431.54/0.885 231.53/0.885 5Set14×230.24/0.868 832.28/0.905 632.42/0.906 333.03/0.912 433.04/0.911 832.99/0.912 433.22/0.913 7×327.55/0.774 229.13/0.818 829.28/0.820 929.77/0.831 429.76/0.831 129.79/0.832 529.88/0.833 8×426.00/0.702 727.32/0.749 127.49/0.750 328.01/0.767 428.02/0.767 028.09/0.770 028.05/0.768 8BSD100×229.56/0.843 131.21/0.886 331.36/0.887 931.90/0.896 031.85/0.894 231.80/0.895 232.01/0.897 4×327.21/0.738 528.29/0.783 528.41/0.786 328.82/0.797 628.80/0.796 328.82/0.798 028.87/0.799 6×425.96/0.667 526.82/0.708 726.90/0.710 127.29/0.725 127.23/0.723 327.32/0.727 527.24/0.724 7平均值28.78/0.800 430.50/0.841 730.64/0.843 131.26/0.854 931.30/0.854 531.30/0.855 831.40/0.867 5
注:粗体标记数字表示最佳效果。

表3 在Set5、Set14和BSD100数据集上不同超分辨率重建方法的平均测试时间 s
注:粗体标记数字表示最佳效果。
不同图像超分辨率重建方法在Set5、Set14和BSD100数据集上进行测试的PSNR和SSIM结果如表2所示,从客观角度评价了图像的重建效果。可以看出,VDSR、DRCN和LapSRN这3种方法比Bicubic、A+和SRCNN这3种方法的峰值信噪比和结构相似度值均有提高;由于SymRCN方法将对称残差引入到了卷积神经网络中,实现了局部和全局特征融合,SymRCN方法较VDSR、DRCN和LapSRN这3种方法的平均峰值信噪比值分别提高了0.14 dB、0.1 dB和0.1 dB,平均结构相似度值分别提高了0.012 6、0.013 0和0.011 7,充分证明了该方法的有效性和重建图像质量的可靠性。除了图像质量评价外,测试时间也是评价超分辨率重建质量的一项重要指标,不同方法在Set5、Set14和BSD100数据集上测试的时间结果如表3所示。从表3中可以看出,SymRCN方法的测试时间虽略高于LapRCN方法的,但综合峰值信噪比和结构相似度两种评价指标,SymRCN方法的整体重建效果更好,效率更高,同时相较于其他5种比较方法所用平均测试时间较短,实际应用中实时性较好。
4 结束语
文中方法将跳跃连接引入图像超分辨率重建,设计了一种长短跳跃连接网络,提出了基于对称残差卷积神经网络的图像超分辨率重建方法。采用对称残差学习以提升收敛速度,采用长短跳跃连接融合全局与局部分级特征,从而保证网络训练的稳定性。实现了残差块内局部信息的充分利用,有效改善了由网络深度带来的梯度消失;同时实现了残差块外全局特征的融合以弥补网络加深丢失的高频细节。实验结果表明,对称残差卷积神经网络方法的重建效果较传统方法有明显的优势,重建图像的视觉效果更贴近人眼感官要求,充分证明了该方法的有效性和实用性。在后续的研究中,将尝试继续拓宽网络宽度和深度以进一步改进网络,寻求其他优化方法以进一步提高重建质量。
