一种结合时刻表调整的列车节能驾驶优化方法
2019-11-08蔡伯根上官伟
盛 昭,蔡伯根,上官伟,2,王 剑 ,2
(1.北京交通大学 电子信息工程学院,北京 100044;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
近年来,我国高速铁路行业发展迅速。截至2016年底,国内高速铁路营运里程已经达到2.2万km,2017年6月25日“复兴号”中国标准动车组在京沪高铁正式双向首发[1],并于9月21日率先实现了时速350 km运营,成为了世界上运营时速最快的高速列车。高速铁路在给广大群众带来快捷便利的同时,大量的能源消耗也成为一个不能忽视的问题。在保障高速列车系统安全可靠的前提下,开展以降低高速列车运营能耗水平为目的的关键理论技术与方法研究具有重要现实意义。有关列车运行节能优化方面的研究可以从以下几个方面考虑:
(1) 车体本身的优化研究:采用轻量化车体的设计以及流线形车头的设计来减少运行中的阻力,使用高效率牵引设备提高能量的利用率。
(2) 轨道线路优化设计的研究:通过减少线路中的坡度、曲线段以及隧道来减少运行中的阻力。
(3) 列车驾驶策略的优化研究:通过速度曲线优化、再生制动的使用减少运行中的能耗。
(4) 列车运输组织的优化研究:通过优化运行图和时刻表降低线路整体运输能耗。
前两方面是线路、车辆设计之初需要重点考虑的问题,本文的研究工作重点关注后两条。文献[2-3]对列车节能驾驶和时刻表优化两个方面的研究工作进行了详细的总结。
在列车操纵优化方面,文献[4]将动态规划法和离散型数学解析法应用于求解水平轨道无限速的列车运行模型。文献[5]提出了基于简单模型的列车运行优化方法,并给出了几种列车运行最优轨迹的描述。文献[6-7]应用极大值原理进行了基于线性能耗优化的列车运行最优工况序列推导,得出了列车节能运行工况序列为最大加速,惰行和最大制动;在长距离运行区间内,列车节能运行工况序列还应包括巡航工况[8]。文献[9]采用惰行控制方法研究了路网环境下的列车节能运行问题。文献[10]采用差分进化算法研究了列车运行操纵的多目标优化问题。文献[11]基于遗传算法研究了以节能为目的的列车控制模型和列车运行调整方法。文献[12-13]与其研究团队在列车运行优化问题上做了大量分析研究,分析了在有限速和无限速两种情况下的最优运行策略。文献[14]研究了多辆列车运行于冲突区段时的运行优化问题,采用黄金分割搜索法求解列车在冲突区段能耗最低的运行速度。文献[15]在列车运行优化的研究中,考虑了铁路系统结构的复杂性和不同列车的载重差异性,提出一种基于能耗与时间的列车调度模型,并利用Pareto优化理论求解该模型的最优解。
在列车运输组织优化方面,文献[16]针对高速铁路列车运行图的优化和评估问题,提出以控制列车晚点传播为主要目的的可恢复鲁棒性优化模型。文献[17]以列车旅行时间和动车组接续时间最小化为目标函数,建立了高速铁路列车运行图综合优化模型,并给出求解方案。文献[18]以最大社会效益为目标建立了公交化城际列车时刻表优化模型。文献[19]通过考虑再生制动最大重叠时间来优化城轨列车的时刻表。文献[20]综合考虑了列车控制优化和时刻表优化的问题,建立了移动闭塞下的多相位最优控制问题,采用Matlab的GPOPS工具箱进行求解。文献[21] 提出了综合描述高速列车时刻表优化和运行曲线优化的“空间-时间-速度”网络框架,并采用动态规划方法进行求解。
综合国内外的相关研究可以发现,目前关于列车运行优化方面已经有大量研究成果,且有部分研究成果已经应用于工程实践。但是大部分研究工作将列车节能驾驶问题和时刻表优化问题单独考虑,综合考虑两者的研究相对匮乏。
基于上述分析,结合我国高速铁路运营的基本特点,本文在以往研究的基础上,研究基于时刻表调整的列车驾驶节能优化方法。首先,建立高速列车多站间运行的离散状态空间模型;然后,以巡航速度、制动初速度为决策变量,以区间运行能耗、运行时间为目标建立高速列车多站间节能运行优化模型,利用基于模拟退火的粒子群算法求解以“能耗-时间”为双目标的Pareto最优解集,并通过最小二乘法拟合得到每个区间相应的Pareto曲线;在此基础上,利用“能耗-时间”Pareto曲线,建立多站间时刻表调整优化模型,基于KKT条件对连续站间的时刻表优化调整问题进行求解,得到最优的站间运行时分组合和最佳区间运行策略。
1 高速列车多站间运行优化问题
1.1 高速列车区间运行基本过程
对于已建成的轨道线路,线路信息是固定的,同时固定型号的列车牵引和制动特性参数也是确定的。因此,高速列车在站间的速度曲线优化是研究列车节能运行的基础。高速列车运行过程中,在列车运行控制系统的监督下根据同一区间前行列车的位置、速度以及线路信息的变化,更新行车许可,根据更新的行车许可终点生成“速度-距离”模式曲线,监控列车的安全运行。列车在站间存在多种可行的速度曲线,根据文献[8],列车在一个区间内的最优驾驶策略为“最大牵引-巡航-惰行-最大制动”。图1中列车通过最大牵引达到最大巡航速度vcr,经过匀速巡航阶段进入无动力惰行阶段,在速度vbr时实施制动,直到在下一站停靠。

图1 高速列车区间运行最优工况策略
1.2 高速列车多站间节能运行优化模型
考虑高速列车在连续站间的运行优化问题。列车从始发站s1出发,途中经过n个连续站间,最终达到终点站sn+1。在第i个区间内列车的运动过程可以表示为

(1)
式中:xi∈[si,si+1],为在第i个区间内列车的位置;vi∈[0,vmax],为在第i个区间内列车的速度,vmax为当前位置最大限速;ti为第i个区间内列车的运行时间;M为列车的质量;γ为列车回转质量系数;Ft(vi)和Br(vi)分别为列车在速度为vi时的最大牵引力和最大常用制动力,可由列车的牵引、制动特性确定;Rs(xi)、Rr(v)分别为列车行驶过程的线路阻力和基本阻力,基本阻力由速度决定;a,b,c为阻力系数;ui,f,ui,b∈[0,1]分别为牵引和制动系数,且和列车的运行状态存在如下关系
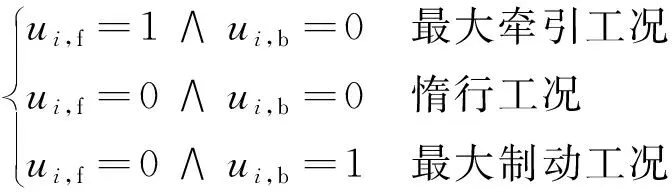
(2)
以CRH2A型高速动车组为例,列车的牵引、制动特性曲线见图2。
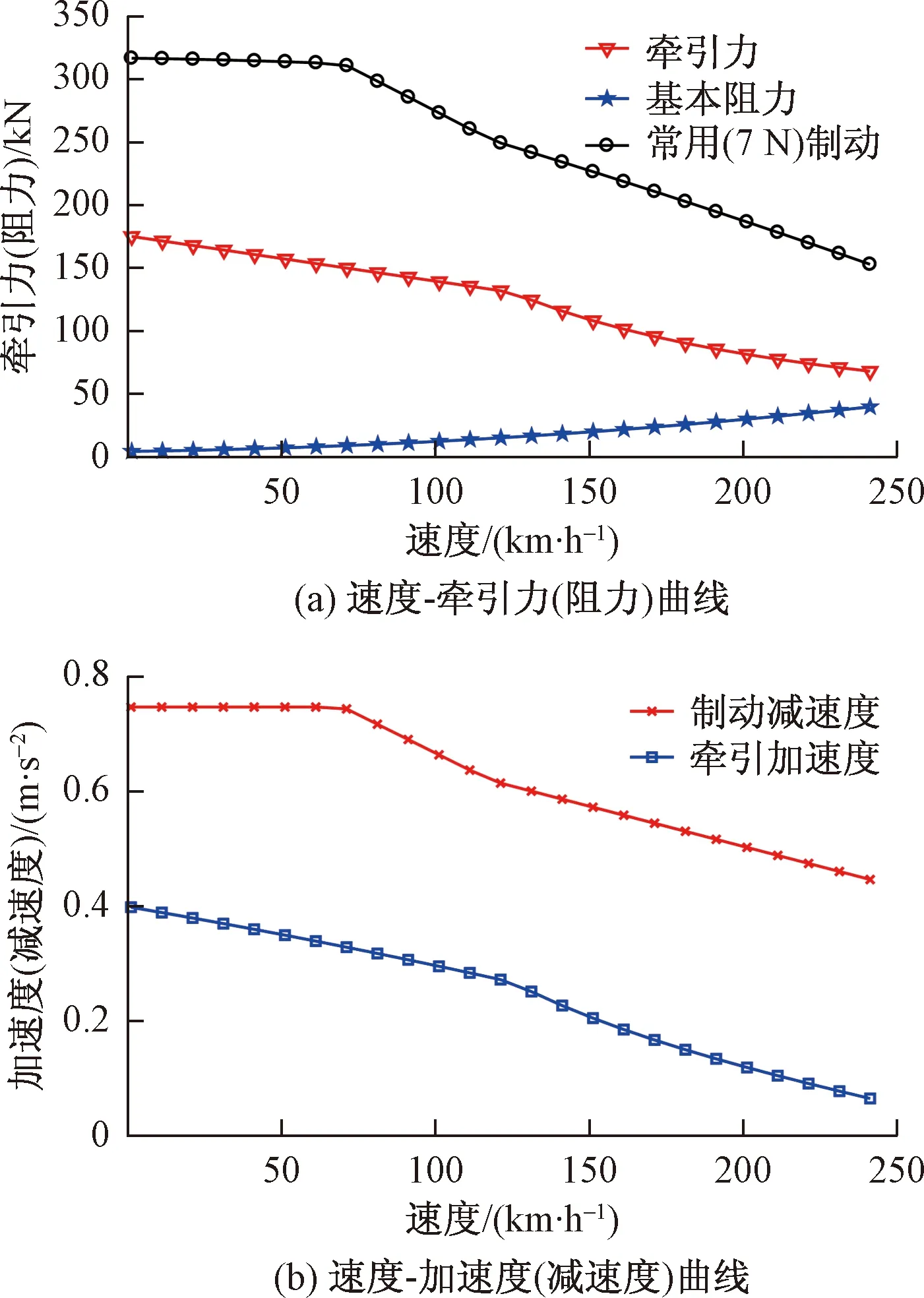
图2 CRH2A高速列车牵引、制动特性
为了实现计算机控制和处理,将距离进行离散化处理,对式(1)的微分项进行前向差分得到
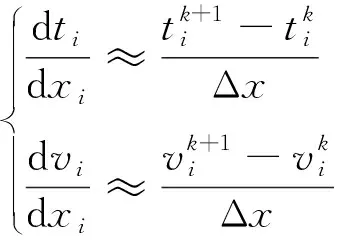
(3)

引入离散状态空间的概念,将式(3)带入式(1)中,以列车位置、速度和运行时间为状态变量,可以得到表征高速列车动力学特征的非线性离散状态空间模型为

(4)
根据图1的最优驾驶策略,在区间i内,巡航速度vcr和制动初速度vbr把列车的运行过程分成了4种模式,因此决策变量vi=(vcr,i,vbr,i)确定了在该区间内列车的速度曲线。区间i包含的离散化子区间的个数Li可以通过式(5)得到,牵引、巡航、惰行和制动的子区间个数和决策变量相关,分别用Li,1,Li,2,Li,3,Li,4表示。

(5)
高速列车的制动方式包括空气制动和电制动等,电制动又包含电阻制动和再生制动。如果制动产生的电能通过电阻发热消耗掉,称为电阻制动;如果制动产生的电能反馈给电网供其他设备使用,称为再生制动。列车高速运行时优先使用再生制动,低速运行时以空气制动为主[22],因此列车运行过程中的能耗主要来自牵引过程,本文在计算列车区间运行能耗时主要考虑牵引和巡航两种工况下的运行能耗,因此由决策变量(vcr,i,vbr,i)确定的列车在区间i运行的能耗和运行时间可以表示为
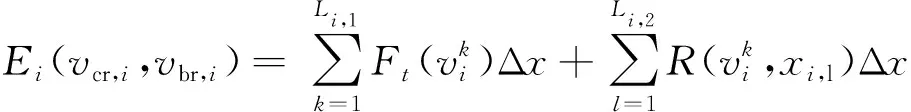
(6)
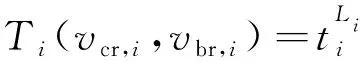
(7)
在整个解空间内,能耗和时间的范围可以确定为Ei∈[Ei,min,Ei,max]和Ti∈[Ti,min,Ti,max]。综合考虑能耗和时间,采用归一化的思想,加权的目标函数可以表示为

(8)
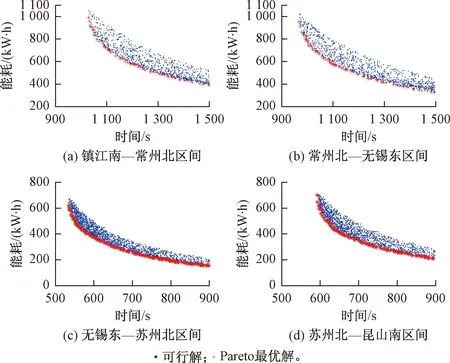
根据式(6)、式(7)和PSO-SA优化算法,可以得到区间i内,按照决策变量v=(vcr,i,vbr,i)建议的驾驶策略运行的能耗和时间见图3。图中每一个点代表一组可行的驾驶策略,也代表了一种可行的列车区间运行速度曲线。

图3 Pareto曲线
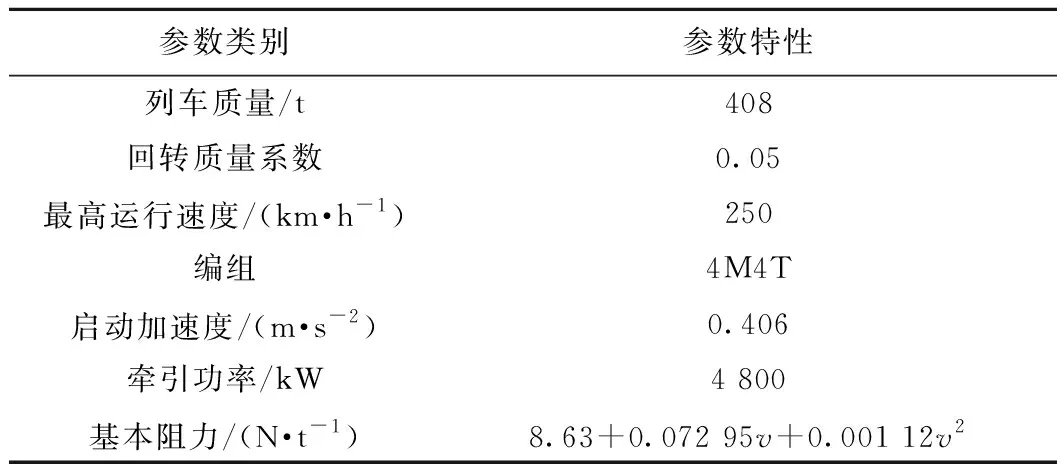
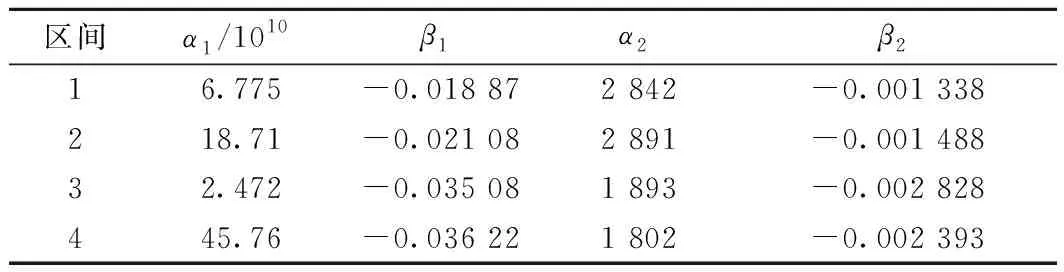
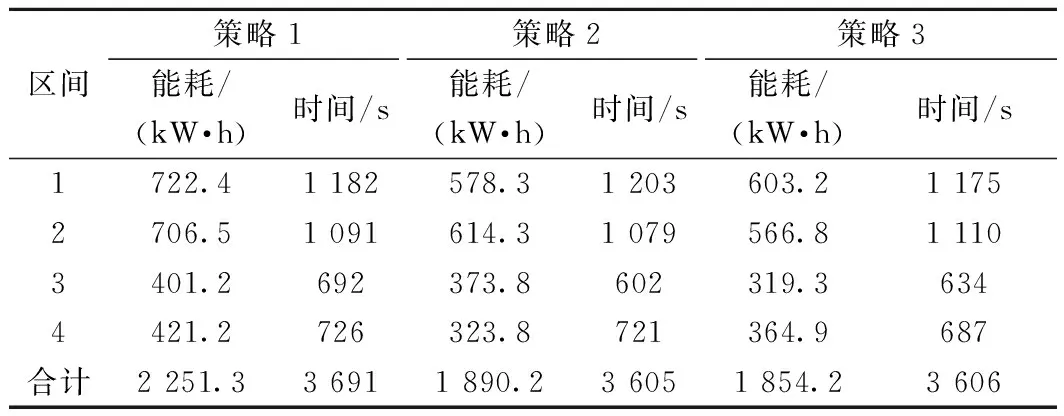
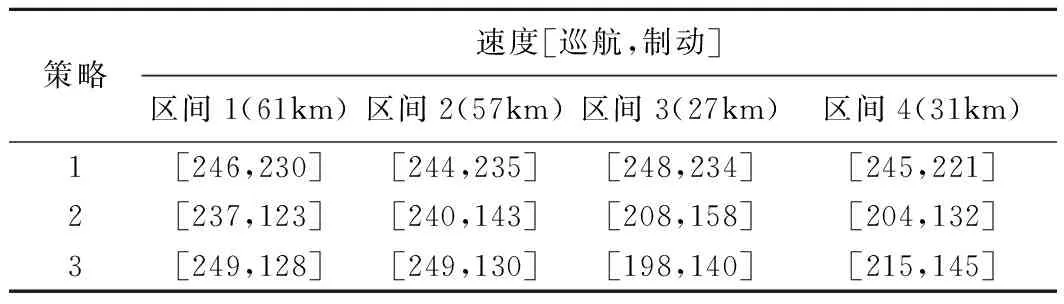
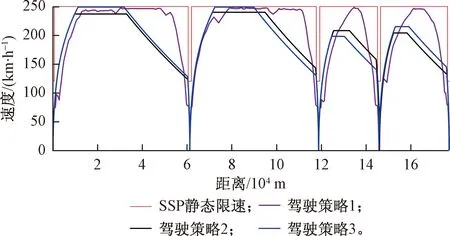
Pareto最优解根据多目标优化理论定义为:在可行空间Ω内,若对于任意的决策变量v∈Ω,不存在v*∈Ω,使得E(v*) 通过最小二乘法拟合逼近可以得到Pareto最优解集的区间运行能耗和时间的函数关系fi(·)。 Ei=fi(Ti) (9) 同理,可以得到列车在每个区间运行过程的最优解集的运行能耗和运行时间的拟合函数Ei=fi(Ti),i=1,2,…,n。因此,列车从始发站到终点站整个运行过程的节能优化问题可以表示为 (10) s.t.Ei=fi(Ti) Ti,min≤Ti≤Ti,max 式中:Tsch为全程多区间总运行时间;Ti,min和Ti,max分别为列车在区间i的最小运行时间和最大运行时间。 为了求解高速列车多站间运行节能优化问题,本文首先在粒子群PSO算法中引入模拟退火SA的思想,增强PSO算法的全局搜索能力,基于改进的PSO-SA算法求解列车单区间运行的以“能耗-时间”为指标的Pareto最优解集,并拟合得到Pareto曲线。根据KKT条件对多个区间列车运行时间进行优化匹配,得到基于时刻表调整的列车节能驾驶策略。 PSO算法是一种基于群体的随机优化技术。每个可能的解都表示为种群的一个粒子,每个粒子都有自己的位置(决策变量)和速度(搜索方向),以及由目标函数决定的适应值,通过追随当前搜索到的最优值来寻找全局最优值。SA算法是一种全局最优的随机性组合优化方法,本文将SA算法引入粒子群的变异操作过程,使得算法在保留PSO算法简单易实现的基础上,提高全局搜索能力。算法的具体实现步骤如下: Step1初始化粒子种群Xg={X1,X2,…,XNP},g表示算法进化的代数,初始化时g=0,最大进化代数用gm表示,NP表示种群规模。其中第k个粒子Xk=(pk,dk)包含了粒子本身的位置信息pk和速度信息dk。位置信息pk=(vcr,vbr)由二维决策变量(巡航速度和制动初速度)确定,速度信息dk同样是二维变量,决定了粒子每次迭代过程变化的步长,即粒子位置信息pk变化的大小。 (11) (12) 式中:ω为惯性权重;c1和c2为最优个体学习因子;r1和r2为相互独立的伪随机数,且服从[0,1]上的均匀分布。 Step4模拟退火选择操作。首先计算更新前后粒子的适应度函数差值。 (13) 基于模拟退火过程计算每个粒子的接受概率为 (14) 式中:TPg为第g次迭代的退火温度。基于模拟退火的选择过程可以表示为 (15) 更新退火温度,其中α为退火系数。 TPg+1=αTPg (16) Step5根据适应度函数的变化和最大进化代数判断算法是否终止。随着算法迭代计算,当种群的最优粒子适应度值不再变化或者当前进化代数满足g≥gm时,算法迭代终止;未达到终止条件则返回Step 2。 根据2.1节的PSO-SA优化算法,可以得到列车在每个运行区间的Pareto最优解集。通过最小二乘法曲线拟合可以得到每个区间的能耗时间解析表达式。采用KKT条件求解式(10)描述的区间运行时刻表调整优化问题。 KKT条件是求解含有不等式约束的凸优化问题的充要条件,是一种扩展的拉格朗日乘子法。可将式(10)写成标准的有不等式约束的优化问题为 (17) h1,j(Tj)=Tj,min-Tj≤0j=1,2,…,n h2,k(Tk)=Tk-Tk,max≤0k=1,2,…,n 式中:T=[T1T2…Tn]为列车各个区间运行时间的向量;g(·)为等式约束条件,表示列车从始发站至终点站总的运行时间固定;h1,j(·)和h2,k(·)为不等式约束条件,分别表示每个区间运行时间的下限约束和上限约束。 本文采用指数函数来拟合能耗时间存在的解析关系,即函数fi(·)为指数函数的线性组合,是典型的凸函数。同时约束条件g(·)、h1,j(·)和h2,k(·)都是具有仿射性的函数,因此式(17)表示的含有不等式约束的优化问题是凸优化问题,可以采用KKT条件求解。 定义含有不等式约束条件的拉格朗日函数为 (18) 式中:参数λ、u1、u2为相应约束条件的乘子。 因此,根据KKT条件可以得到时刻表调整优化问题的求解方案,即 (19) 其中,微分项∂L/∂Ti=0用来求解函数的极值点;在KKT条件中等式约束的乘子λ不能为零,不等式约束的乘子u1,j、u2,k需要满足非负性;同时经过乘子作用的约束项λg(T)、u1,jh1,j、u2,kh2,k必须等于零才可以保证拉格朗日函数和原优化函数等价。 由KKT条件,可以得到最优的节能运行时刻表T*,也就确定了列车每个运行区间最佳的巡航速度和制动初速度,从而得到优化的列车区间运行速度曲线。基于时刻表调整的列车驾驶节能优化方法流程见图4。 图4 算法流程 为了验证基于时刻表调整的列车驾驶节能优化方法的有效性,以2015年1月D3096次动车组在全长176 km的区段实际运行数据为依据进行仿真测试,该区段共包含5个连续车站,共4个区间:镇江南—常州北—无锡东—苏州北—昆山南。列车和各区间的基本参数如表1、表2所示。 表1 CRH2A型列车主要参数 表2 镇江南—昆山南区间运行信息 根据2.1节的PSO-SA算法,求解每个区间的最优的巡航速度和制动初速度,得到以能耗和时间为指标的Pareto最优解集,结果见图5。根据最优解集可以看出区间能耗和时间之间存在明显的负相关关系。本文采用了指数函数来表征每个区间能耗-时间之间的拟合函数关系,具体的函数表达式为 Ei=fi(Ti)=α1eβ1Ti+α2eβ2Ti (20) 式中:α1、β1、α2、β2为拟合参数。 图5 区间Pareto最优解 图6给出了每个区间基于最小二乘法的Pareto拟合曲线。4个区间的拟合结果如表3所示。 图6 “能耗-时间”拟合曲线 区间α1/1010β1α2β216.775-0.018 872 842-0.001 338218.71-0.021 082 891-0.001 48832.472-0.035 081 893-0.002 828445.76-0.036 221 802-0.002 393 在拟合能耗-时间Pareto曲线基础上,根据式(19)所列的KKT条件,得到时刻表的最优调整策略和优化后的列车站间运行时分。表4给出了列车实际驾驶策略、准点最优驾驶策略和基于时刻表调整的最优驾驶策略的区间运行能耗和运行时间的分析。实际驾驶策略(策略1)以列车车载设备实测记录数据和《列车牵引计算规程》[23]作为依据;准点驾驶策略(策略2)采用本文提出的PSO-SA优化算法求得,在满足准点的基础上实现最节能驾驶,即在图6拟合曲线上搜索最接近准点要求的最优解;基于时刻表调整的最优驾驶策略(策略3)是在本文PSO-SA优化算法的基础上,采用KKT条件求解,得出时刻表调整后的最节能驾驶策略。根据表4可以看出,基于PSO-SA算法的准点驾驶策略相比实际列车运行策略,能耗降低了16%;基于时刻表调整的最优驾驶策略在准点驾驶策略的基础上能耗降低了1.9%,优化前后的列车区间运行时分见图7。 表4 3种驾驶策略区间运行结果 图7 区间运行时分 优化前后每个区间的巡航速度和制动初速度如表5所示,图8给出了相应的三种驾驶策略的速度曲线。可以看出相对于驾驶策略1而言,驾驶策略2在按照既有时刻表运行的条件下增加了惰行工况时间来减少区间运行能耗;同时对于站间距较短的区间(区间3和区间4),由于较大的巡航速度会导致较早的制动,所以本文的优化方法减小了站间距较短的区间巡航速度,有效地降低了列车的运行能耗。驾驶策略3基于站间的运行时间匹配,调整列车运行时刻表,可以在驾驶策略2的基础上进一步减少列车运行能耗。结果表明,和列车实际驾驶策略相比,结合PSO-SA算法和KKT条件调整时刻表后的最优驾驶策略可以降低17.6%的站间运行能耗。 表5 区间巡航速度和制动初速度 km/h 图8 三种驾驶策略速度曲线 本文针对高速列车在连续站间运行的节能优化问题,建立了表征高速列车动力学特征的非线性离散状态空间模型和高速列车节能驾驶策略优化模型;采用基于模拟退火的粒子群算法求解最优的区间运行策略,得到以区间运行能耗和运行时间为目标的Pateto最优解,利用 KKT条件求解最佳的站间运行时分组合;本文以高速列车在镇江南—昆山南连续站间的运行数据为基础进行仿真测试。仿真结果表明,通过增加惰行工况运行时间和优化站间运行时间可以有效地实现最优化节能驾驶。本文的研究结果可以为列车运行区间巡航速度的选择、惰行工况的利用和连续站间时刻表优化提供参考。 本文仅考虑了单车在连续站间运行的节能优化问题,随着客流量的增大和发车间隔的减小,多车追踪运行情况下的相互影响和再生制动能耗的利用是今后研究的方向。
2 高速列车节能运行优化方法
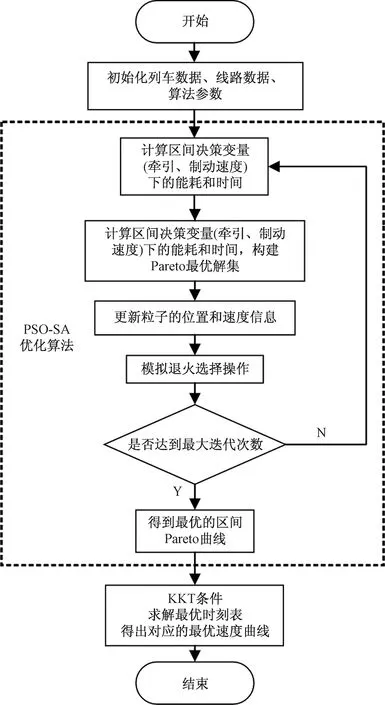
2.1 基于PSO-SA算法的区间运行优化过程
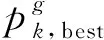
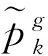
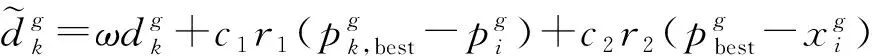



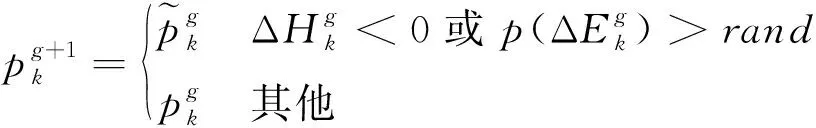
2.2 基于KKT条件的时刻表调整优化
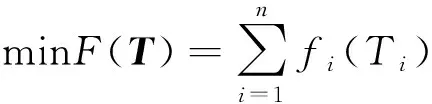

3 仿真验证结果分析



4 结束语
