Polarized Debye Sheath in Degenerate Plasmas∗
2019-11-07ShahmansouriandMisra
M.Shahmansouri and A.P.Misra
1Department of Physics, Faculty of Science, Arak University, Arak, P.O.Box 38156-8-8349, Iran
2Department of Mathematics, Siksha Bhavana, Visva-Bharati (A Central University), Santiniketan-731 235, India
Abstract The force on a charged dust grain in a plasma due to polarization of thermal ions and degenerate electrons around the grain is derived in the limits of weakly relativistic and ultra-relativistic degeneracy of electrons.It is found that in both these cases, the magnitude of the polarization force is enhanced compared to that in classical plasmas.The influence of this force on dust-acoustic (DA) modes is examined and discussed.It is shown that the DA wave frequency in degenerate plasmas is significantly reduced compared to the classical DA mode.
Key words:degenerate plasma, polarization force, dust acoustic waves
1 Introduction
Pioneering works of Hamaguchi and Farouki[1−2]that introduced the concept of a polarization electrostatic force(known as the polarization force) due to the polarization of plasma particles around charged dust grains in a nonuniform plasma, provide a new opportunity for describing the physics of nonuniform plasmas.The occurrence of such force is directly linked to astrophysical environments and industrial plasmas where the medium is truly nonuniform.The influence of the polarization force on dust-acoustic (DA) modes has been a topic of important research during the past many years.[3−14]Such force,not only modifies the wave frequency, but also affects the dynamical behaviors of DA perturbations.In fact,the propagation characteristics of collective modes can be modified due to the contribution of the polarized Debye sheath.[9]In a recent work, a generalized form of the polarization force has been obtained in charge varying dusty plasmas with applications to DA waves.[10]Furthermore, the contribution of nonthermal species on the polarization force has also been examined.[13]
Regarding the practical importance of the polarization effect it must be added that however the polarization force in some typical experimental situations remain negligible relative to the other present forces (such as electrostatic force), but in some other cases such as in low frequency DA wave situation[3]it is no longer negligible(which is important in different plasma situations ranging viz., dc-discharge, rf-discharge magnetron devices, and Q machines[15−16]).Thus, when the polarization effect is considerable it may affect the propagation of electrostatic waves through the modifying the phase velocity of these waves.Consideration of the polarization force exerts an upper limit on the dust grain size through which affect the propagation of such waves.
The collective behaviors of charged particles in dusty plasmas have been studied during the last few decades because of their potential applications in laboratory,space and astrophysical plasmas.[15]It is also well known that the quantum effects can play vital roles even in dense dusty plasmas with degenerate species such as those in compact astrophysical objects(viz., white dwarfs and neutron stars)[17−19]as well as in industrial plasma systems[20−22](viz., laser-matter interaction and microelectronic devices).
The dust particles in dusty plasmas are shielded by electrons and ions, with the Debye length beingλD=whereλDeandλDiare the electron and ion Debye lengths respectively.In dusty plasmas with non-degenerate species whereTe ≫Ti, whereTe(Ti) is the electron (ion) thermodynamic temperature,we haveλD ≈λDi.However, in a dense dusty plasma,when the dust particles are shielded by thermal ions and degenerate electrons, the Debye lengthλDis modified and to be replaced by the effective screening lengthwithanddenoting, respectively, the Thomas-Fermi(TF)length and the Fermi energy.[23]Here,meis the electron mass,is the reduced Plancks constant andne0is the equilibrium electron number density.Note that the effective screening lengthλeffdiffers considerably from the Debye lengthλD[24−25]and that the explicit form ofλeffis unknown, however, its value can be estimated via some numerical analysis.In this context,some efforts have been made to find its dependence on the plasma parameters.[24−26]
In the present work, we derive the expressions for the polarization force due to polarization of thermal ions and relativistic degenerate (in weakly and ultra-relativistic limits) electrons in dense dusty plasmas.As an illustration, we examine its influence on DA modes and find that the DA wave frequency in degenerate plasmas is significantly reduced compared to that in classical dusty plasmas.[3]
2 Theoretical Model
We consider an unmagnetized dense dusty plasma consisting of relativistic degenerate electrons, thermal ions and positively or negatively charged dust grains.We can reasonably neglect here the dust charge fluctuation as its influence is not so important in the present study and also the dust charging frequency is much greater than the dust-plasma frequency or DA wave frequency.[27−28]In order to estimate the total force acting on a test charge, we consider the shielding-polarization force, besides the contributions from the pressure gradient force and the electrostatic field force that arise from the ambient plasma.Such polarization force, which is electrostatic in nature,may also appear in a non-uniform degenerate dusty plasmas due to an asymmetric distribution of plasma species.In this case, the screening length (due to TF shielding in non-relativistic or weakly relativistic degeneracy limit)is dependent on the position of the charged particles and thus yields an asymmetric shielding.So,in non-relativistic degenerate plasmas the polarized TF shielding gives rise to a new electrostatic force, besides the usual electric force,with denoting the electric charge of dust particulates andEthe electric field.In the ultra-relativistic degeneracy limit a similar situation can also occur.We denote the screening length in ultra-relativistic and non-relativistic limiting cases are, respectively, byand, the explicit expressions of which will be obtained later.
It is to be noted that for the electric potential at a distance(up to several Debye lengths)from the charged dust grain the Debye-Huckle (Yukawa) profile fits reasonably well even in highly nonlinear regime with an appropriate choice of the effective screening lengthλeff, i.e.,

In the linear regime and in dusty plasmas with thermal ions and non-relativistic or ultra-relativistic degenerate electrons, the effective screening length is given by[29]withλDidenoting the ion Debye length.However, the linear approximation may no longer be valid for complex plasmas.Nevertheless, numerical analysis[26]of nonlinear Poisson-Boltzmann equations ensures that the expression(1) is still applicable but with a definition of an effective dust charge.[30−31]It has also been shown that far from the particle position, the potential drop (due to Debye shielding) is not exponential but shows a power law behavior.[26,31]In the vicinity of the particle, the expression (1) works reasonably well.Accordingly, similar to that proposed by Hamaguchi and Farouki[1]for polarization force due to the polarized Debye sheath in classical plasmas, the electrostatic polarized-screening force acting on a charged dust particulates in degenerate plasmas can be defined as[3]

In the linear regime of classical dusty plasmas (recognized by the nonlinearity parameterβT=Qe/λDkBTi,wherekBis the Boltzmann constant andTiis the ion temperature) for which the effective screening lengthλeffis replaced by the Debye lengthλD,Eq.(2)reduces to the conventional polarization force[3]Fp=−Q2∇λD/2λ2D.We are interested to derive the expressions for the polarization force in dense dusty plasmas by considering classical thermal ions and both the weakly relativistic and ultra-relativistic degenerate electrons.Thus, to drive a closed expression for the Polarization force we first derive an expression for the screening-length in degenerate dense dusty plasmas.In the nonrelativistic or ultra-relativistic degenerate case, the nonlinearity parameter, defined as(the ratio of the Coulomb radius of interaction between thermal ions and charged dust particles, and the linear screening length) may be higher than unity and so the linear approximation for the polarization force may not be valid.Thus,λeffdiffers considerably from the linear limitλL.[24−25]An estimation for the effective screening length as a function of the nonlinearity parameterβLcan be obtained based on the results of Refs.[24, 26]as

3 Derivation of Polarization Force
The energy distribution of degenerate electrons is no longer in the form of thermal distribution (because of the exclusion principle), but is governed by the Fermi energy.In the non-relativistic limit, the equation of state for the degenerate electron species is given by[29]

whereneis the electron number density.Thus, from the momentum balance equation for electrons withme ≪md,and using Eq.(4) we obtain the following distribution function for the electron number density[29]

The ion species are supposed to follow the Boltzmann distribution, given by, unction for the electron number density[29]

whereni0is the equilibrium ion number density.
Next, to obtain an expression for the linear screening length we consider the linearized Poisson equation of the format the position of a spherical dust grain (located at the origin), and use Eqs.(5) and (6).Thus, the linear screening length in the nonrelativistic degenerate case is obtained asλnrL=withdenoting the electron Thomas-Fermi screening length.In this case the polarization force can be obtained from Eq.(2) as
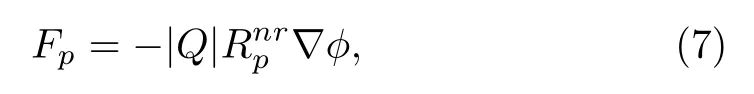
whererefers to the polarization coefficient, given by,

Equation (8) shows thatincreases almost linearly withand its values remain smaller than unity ifOtherwise, as we will see later that for values of1, the DA wave mode becomes unstable, and this corresponds to dusty plasmas with large size of dust grains[3]which may not be so realistic.It seems appropriate here to add that,regardless of the sign of the dust particulates,the polarized-screening force always tends to decrease the screening length.Also, such polarization force is independent of the polarity of dust particulates and for negatively charged dust particles it is always directed opposite to the electric-field force.
For degenerate plasmas, we haveχe ≡ TFe/Te=1 withdenoting the thermal de Broglie wavelength.Typically, for ultra-dense plasmas such as those in compact astrophysical objects (e.g., magnetars, white dwarfs[17]), in whichne0∼2×1027cm−3,nd0∼1.9×1021cm−3,Zd0∼103,we obtainTFe∼6.7×107K.Thus, electrons are degenerate forTe6.7×107K.While in semiconductor quantum wells[20](in whichne0∼5×1016cm−3,nd0∼1011cm−3,Zd0∼103) electron species may be degenerate atTe5.7 K.
Next, we define the non-dimensional parameterse=pe/mecwithpe=(3h3ne/8π)1/3denoting the momentum of electrons on the Fermi surface andcthe speed of light in vacuum.Then, the ultra-relativistic and non-relativistic limits of degeneracy pressure can be determined by assumingse ≫1 andse ≪1 respectively.For ultra-relativistic degenerate electron species, the equation of state is given by[29]

Using Eq.(9) and the momentum equation for electrons,the following distribution function can be obtained for the electron number density,[29]
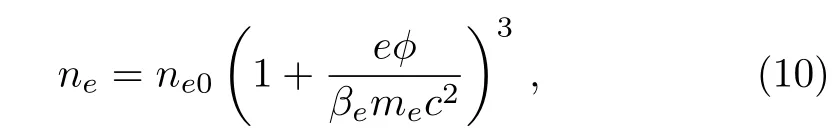

In what follows, we obtain some numerical values of the polarization coefficientwhich will be useful to compare the polarization force so obtained with the electrostatic force.In fact, it represents the ratio of the polarization force and the electrostatic force, i.e.,=, whereFEstands for the electrostatic force.For typical astrophysical parameters withne0=2×1027cm−3,nd0=1.9×1021cm−3,Zd=103,TFe=107K andTi=105K, the polarization coefficient is obtained as=0.133.Also, for typical laboratory parameters (e.g., in metals) satisfying the nonrelativistic degenerate conditions, viz.,ne0=1022cm−3,Te=104K, andTi=300 K, the polarization coefficient is=0.036.Furthermore, for typical values ofne0=1036cm−3,Te=1010K, andTi=107K, and satisfying both the ultra-relativistic and degenerate conditions (viz.,se ≫1 andχe >1), the polarization coefficient is=0.158.On the other hand, for typical complex plasma parameters[3]witha ∼1µm,Q=103e,λD ∼10−2cm,andTi=0.03 eV,we have the polarization coefficient in classical complex plasmas,=0.12.Thus, it follows that the polarization force in degenerate dense plasmas becomes higher in magnitude than that in classical plasmas, and should play vital roles on the linear DA modes as well as nonlinear evolution of DA waves in dense plasmas.
The polarization force can also be compared with the thermodynamic pressure gradient force in dusty plasmas.
The ratio of the polarization and thermodynamic pressure gradient forces is|Fp/FTP|=(c2s+v2th), withvthdenoting the thermal velocity of charged dusts andcsthe characteristic acoustic speed of DA waves.For typical plasma parameters withcs ∼0.1vthandcs ∼2vth,we have|Fp/FTP|∼1.1and |Fp/FTP|∼3Rnrprespectively.It turns out that the importance of the polarization force depends on the dusty plasma environments.In fact,in dense plasma environments, the effects of this force must be taken into consideration.

Fig.1 (Color online) The variations of the normalized screening lengths λnr(ur)/λ0 as a function of the normalized electrostatic potentials eϕ/kBTFe and eϕ/βmc2 are shown in (a) non-relativistic and (b) ultra-relativistic limits.
4 Influence of Polarization Force on DA Waves
We now discuss the influence of the polarization force on DA waves in the limits of non-relativistic and ultrarelativistic degeneracy pressure of electrons with dust particles as heavy point masses with constant negative charge.[31]The dynamics of linear DA waves is governed by the following set of fluid equations.

where the subscripts 0 and 1 stand for the equilibrium and the perturbed physical quantities.The first term on the right hand side of Eq.(13) is the conventional electric force, while the second one refers to the polarization force.Next, Fourier analyzing Eqs.(12) to (14), one can obtain the linear dispersion relation of DA waves in nonrelativistic/ultra-relativistic degenerate dense plasmas as


Thus, the polarization force induces an effective dust charge or an effective dust number density, which results into the reduced DA wave frequency and the DA phase speed by the factorThis is in consequence to the fact that the polarization force of electrons and ions,which produces the DA mode, reduces the restoring force(i.e.,Fr=FE −Fp, withFEdenoting the electric field force), and hence the reduction of the DA phase speed and the DA wave frequency.This reduction appears to be significant when the polarization parameterapproaches the unity.In fact,for1 the right hand side of Eq.(13) is no longer a restoring force, and so the DA waves (given by Eq.(15)) transit from propagating modes to the aperiodically growing noises.[3,33−34]
5 Conclusion
We have derived the explicit expressions for the polarization force that can appear in dense dusty plasmas due to the polarization of relativistic degenerate electrons and thermal ions around charged dust grains.We have considered the two limiting cases of interest in which the degeneracy pressure of electrons are non-relativistic (or weakly relativistic) and ultra-relativistic.It is found that in both the cases, the magnitudes of the polarization forces are enhanced (compared to that in classical plasmas) due to increase of the polarization coefficient which typically depends on the non-linearity parameter.The latter appears to be larger in magnitude than that in classical plasmas.[3]The influence of the polarization force is also examined on DA modes in degenerate dense dusty plasmas.It is found that DA wave frequency and the DA wave phase speed are significantly reduced compared to the classical results.[3]This reduction is due to the reduced restoring force of electrons and ions and so is the dust number density or dust plasma frequency.The results should be useful for understanding the localized electrostatic disturbances in laboratory and astrophysical dense dusty plasmas.
杂志排行
Communications in Theoretical Physics的其它文章
- Numerical Study on the Whole Process of Fireball Evolution in Strong Explosion∗
- Neural-Network Quantum State of Transverse-Field Ising Model∗
- Magnetocaloric Effect in Anisotropic Mixed Spin–1 System:Pair Approximation Method
- Structure, Electronic, and Mechanical Properties of Three Fully Hydrogenation h-BN:Theoretical Investigations∗
- Similar Early Growth of Out-of-time-ordered Correlators in Quantum Chaotic and Integrable Ising Chains∗
- Fractional Angular Momentum of an Atom on a Noncommutative Plane∗
