Geodesic Structure of a Non-linear Magnetic Charged Black Hole Surrounded by Quintessence∗
2019-11-07LiLiShi师丽丽JianPingHu胡建萍YuZhang张钰ChenMa马宸andPengFeiDuan段鹏飞
Li-Li Shi (师丽丽), Jian-Ping Hu (胡建萍), Yu Zhang (张钰), Chen Ma (马宸), and Peng-Fei Duan (段鹏飞)
1Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China
2Geological Resources and Geological Engineering Postdoctoral Programme,University of Science and Technology,Kunming 650093,China
3City College,Kunming University of Science and Technology,Kunming 650051,China
Abstract This paper aims to investigate the geodesic motion in the spacetime of a non-linear magnetic charged black hole surrounded by quintessence.By varying the Lagrangian corresponding to the metric,the orbital motion equation has been obtained.The effects of the magnetic charge Q,positive normalization factor C,angular momentum b,and energy E on time-like and null geodesic motion are discussed from three aspects: orbital stability,orbital types,and circular orbits.By comparing the effects of the above parameters C,b on the effective potential,it is found that quintessence has an impact on the types and stability of orbits.In addition,for time-like orbital motion,when 3.443113 ≤b ≤6.392 578(for fixed C=0.0002,M=1,Q=0.7),there are bound orbits,and within this range,the stable circular orbits exist,and the radii of the innermost and outermost stable circular orbit are r =5.912 654 and r =56.745 933,respectively.For null orbital motion,the orbital types have only unstable circular orbit which occur at r=2.951 072 (E2 = E22=0.4),absorb orbits and escape orbits,but no stable circular orbits,and bound orbits.
Key words: effective potential,orbital stability,orbital types
1 Introduction
Cosmological observations such as the cosmic microwave background,baryon acoustic oscillation,Hubble measurements,and the supernovae type Ia[1−2]suggest that our universe is undergoing an accelerated phase of expansion.Astrophysicists and cosmologists believe that the reason for the accelerated expansion of the universe is due to dark energy.[3−4]According to observations,more than seventy percent of the universe are composed of dark energy.
Quintessence is one of the candidates for dark energy,with negative state parameterwq(the ratio of pressure to density),and−1< wq < −1/3.In 2003,Kiselev[5]derived a spherical symmetric solution of the Einstein equations describing the Schwarzschild black hole surrounded by quintessence,which attracted wide attention of researchers.Using WKB approximation approach,quasinormal modes of a black hole surrounded by quintessence have been studied in Refs.[6–14].The existence of Nariai type black holes with quintessence for special values of the parameters in the theory has been shown by Fernando.[15]And he also investigated the properties of the charged black hole surrounded by the quintessence.[16]The solution of non-linear magnetic charged black hole surrounded by quintessence is derived in Ref.[17].The quintessence around the black hole also corrects the thermodynamic quantities.By using the improved brick-wall model,Maet al.[18]evaluated the entropy of a Schwarzschild spacetime surrounded with the quintessence.In Ref.[19],a solution of Einstein equations with quintessential matter surrounding a d-dimensional black hole is found,then the Hawking radiation in this black hole background has been investigated.Azreg-Anou[20]has obtained the quintessencedependent enthalpy and new extreme solutions in charged de Sitter-like black holes.The thermodynamic stabilities of uncharged and charged black holes surrounded by quintessence have been studied in Ref.[21].
Furthermore,the study of the geodesic structure helps us to understand different gravitational properties of a gravitational center,especially in the strong field regime,like neutron stars and black hole.In recent years,the field on the geodesic motion in the black hole became a fertile ground for researchers[22−37]from different point of view.In Schwarzschild AdS black hole spacetime,a complete discussion for the geodesic motion has been made in Ref.[38],they found all kinds of orbits,which are permitted according to the energy levels.Enolskiiet al.[39]studied the particle motion in Kehagias-Sfetsos black hole spacetime,which is a static spherically symmetric solution of a Horava-Lifshitz gravity model.Malakolkalami and Ghaderi[40]analyzed the null geodesics and all types of orbital motion in the Schwarzschild-anti de Sitter black hole surrounded by quintessence spacetime by means of the effective potential for the photons.
In this paper we discuss geodesic motion in the spacetime of the non-linear magnetic charged black hole surrounded by quintessence.The organization of this work is as follows.In the second sections,we obtain the equations of geodesic motion by varying the Lagrangian.In the third and fourth sections,we mainly concentrate on the influence of magnetic chargeQ,energy levelsE,positive normalization factorC,angular momentumbon the geodesic motion of time-like and null.In the last section,the conclusion is drawn.
2 Equations of the Orbital Motion
The metric of the spacetime of non-linear magnetic charged black hole surrounded by quintessence is given by[17]
with

whereMdenotes the black hole mass,Crespects the positive normalization factor,Qis the magnetic charge.wqis the quintessential state parameter,which is constrained to the interval−1< wq < −1/3.It is obvious that whenC=0 the metric is the Hayward-like black hole metric; whenQ=0 the metric is the Schwarzschild solution surrounded by quintessence; whenQ=0,C=0 it is the Schwarzschild black hole one.Then,from here on we put particle massm=1,this means that the related parameters are expressed in units ofm.The Lagrangian corresponding to the metric Eq.(1) is
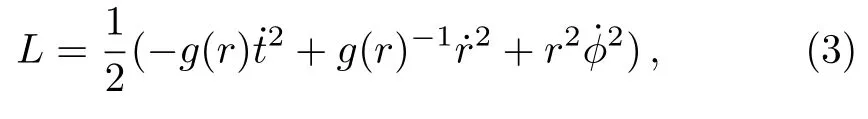
where a dot represents differentiation with respect to the affine parameter,τ.The Euler-Lagrange equation is
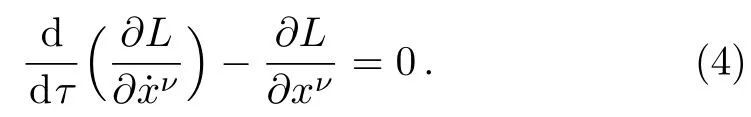
By substituting Eq.(4) into Eq.(3),we can get
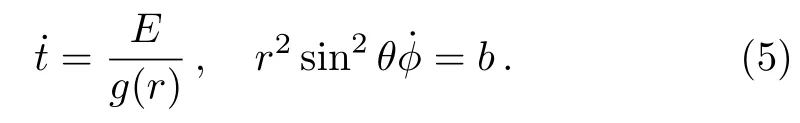
Without loss of generality,we putθ=π/2.Then Eq.(5)can be written as
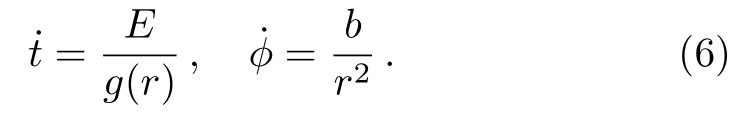
Substituting Eq.(6) into Eq.(3),we can get

Here,the effective potential equation can be defined as
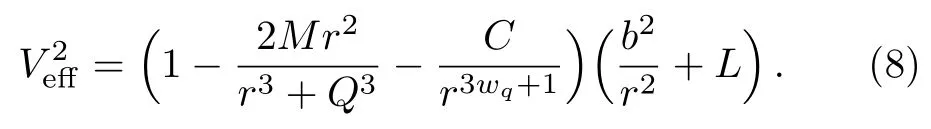
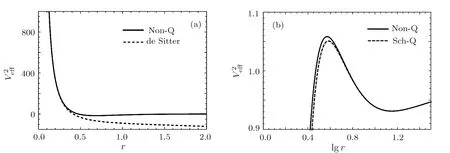
Fig.1 (a)The behaviors of the effective potential of particle in non-linear magnetic charged black hole surrounded by quintessence(Non-Q)and de-Sitter geometry for fixed b=4.2,M =1,Q=0.7,C =0.0002.(b)The behaviors of the effective potential of particle in non-linear magnetic charged black hole surrounded by quintessence(Non-Q)and Schwarzschild black hole surrounded by quintessence (Sch-Q) for fixed b=4.2, M =1, Q=0.7, C =0.0002.

Fig.2 (a)The behaviors of the effective potential of particle with different wq for fixed other different parameters.Line 1 represents wq = −0.4, C=0.001, b=4.3, M=1, Q=0.5; Line 2 represents wq = −0.6, C=0.0008,b=4.2, M=1, Q=0.7; Line 3 represents wq = −0.8, C=0.0008, b=4.1, M=1, Q=0.5; Line 4 represents wq = −0.8, C=0.0006, b=4.0, M=1, Q=0.3.(b) The behaviors of the effective potential of particle with different wq for fixed b=4.2, M =1, C =0.0002, Q=0.7.
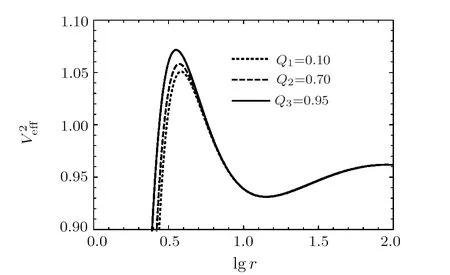
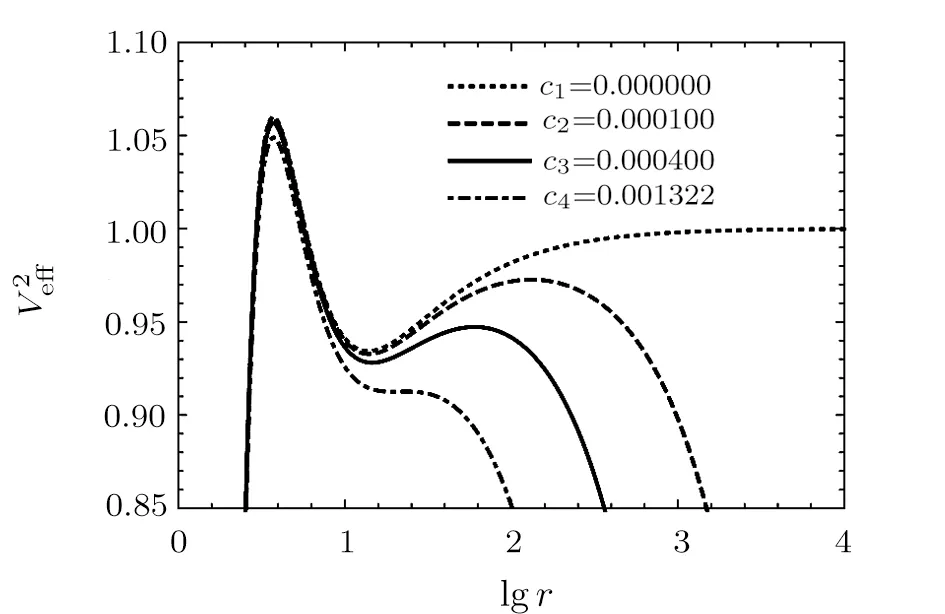
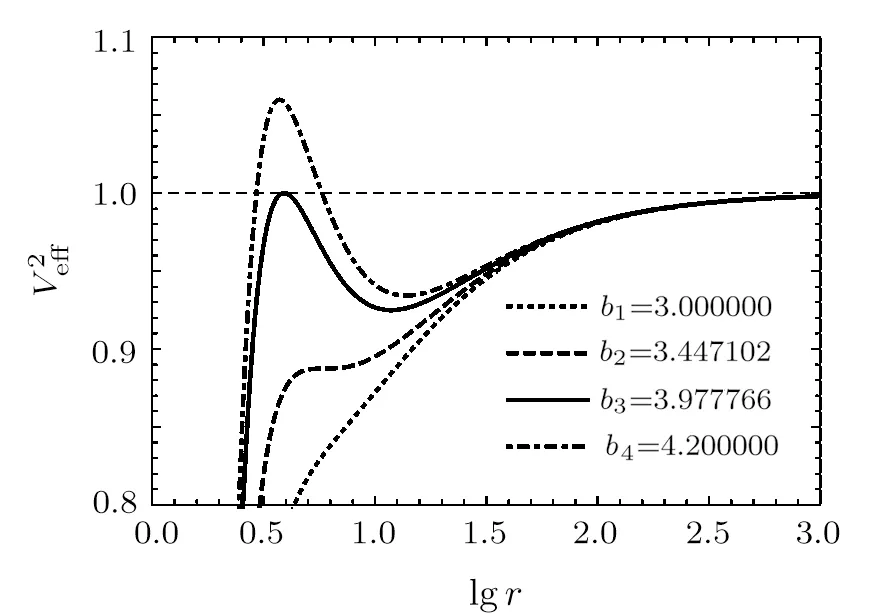
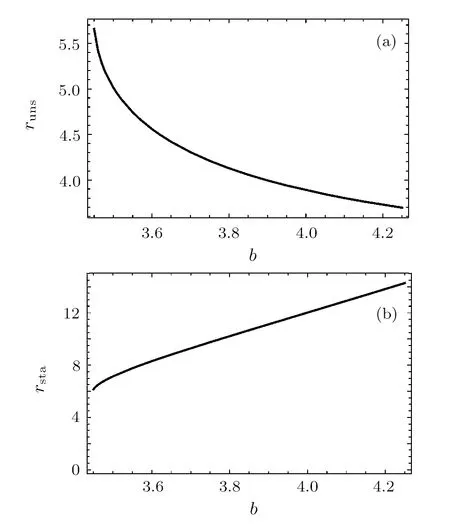
Now we have obtained the effective potential equation in the non-linear magnetic charged black hole surrounded by quintessence spacetime.Interestingly,in the case of short distances (Q/r ≫1),the functiong(r)≃1−Λr2/3−C/r3wq+1,with Λ=6M/Q3,the effective potential equation isV2eff =g(r)(b2/r2+1).Comparing the two curves in Fig.1(a),we can see that the behavior curves of non-linear magnetic charged black hole surrounded by quintessence spacetime and de-Sitter geometry are very similar asQ/r ≫1.However,there is no circular orbit in de-Sitter geometry.In the case of large distances(Q/r ≪1),the functiong(r)=1−2M/r −C/r3wq+1,the effective potential equation isV2eff =g(r)(b2/r2+1).It is shown in Fig.1(b) that the behavior of the effective potential of particle in non-linear magnetic charged black hole surrounded by quintessence is similar to a Schwarzschild black hole surrounded by quintessence,especiallyQ/r ≪1.Furthermore,Fig.2(a) shows the behaviors of the effective potential of particle with differentwqfor fixed different values of other parametersQ,C,b.In order to better analyze the orbital types of particle or photon with various parameters,we consider the parameter range that can make the orbital types at most (the existence of stable circular orbits and bound orbits).Takingb=4.2,M=1,C=0.0002,Q=0.7 as an example,Fig.2(b)clearly shows that when−0.838 356≤wq < −1/3,the orbital types are the most,including absorb orbits,unstable circular orbits,stable circular orbits,bound orbits,and escape orbits; when−1 In the case of time-like geodesics,we have thatL=1,Eq.(8) can be rewritten as follows: In this section,we aim to obtain the influence of positive normalization factorC,magnetic chargeQ,angular momentumb,and energyEon the geodesic motion for fixed black hole massM=1. In Fig.3,the dependence of the effective potential is shown with different values ofQfor fixedb=4.2,M=1,C=0.0002.From this figure one can easily see that with the decrease of magnetic chargeQ,the peak of curves is going to be decreased,the location of peak and the intersection of the effective potential andr-axis come far away the central of black hole.Moreover,one can conclude from Fig.4 that asQincreases,the radius of the unstable circular orbit decreases,while the radius of the stable circular orbit increases.In this case,the radius of the unstable and stable circular orbit in Schwarzschild and Schwarzschild solution surrounded by quintessence (Sch-Q) are 3.832 776,13.807 224; 3.833 210,14.162 434,respectively.Comparing the radius of circular orbit under three spacetime conditions,we can see that for the radius of unstable circular orbit:rSch-Q> rSch> rNon,for the radius of stable circularrSch Fig.3 The behaviors of the effective potential of particle with different Q for fixed b=4.2,M =1,C =0.0002. In the case ofC=0,there is no quintessence,the equations of the orbital motion,and the corresponding effective potential are as follows: In the case ofC ̸=0,there is quintessence,then the equations of the orbital motion and corresponding effective potential are as follows: For the circular orbits,the corresponding effective potential must satisfy In order to obtain a critical value that can be used to determine the occurrence of a stable circular orbit,we still need guarantee follows equation simultaneously Fig.4 The radius of the unstable circular orbit runs(a) and the radius of the stable circular orbit rsta (b) of particle with different Q for fixed C=0.0002, M=1,b=4.2. By solving the above Eq.(13) to Eq.(16),we get the critical valueC=0.001 322,which represents the radius of the outermost circular orbit isr=21.236 694 3.In Fig.5,the effective potential of the particle motion with differentCis shown,where we fix parametersb=4.2,M=1,Q=0.7.WhenC ≤0.001 322,for exampleC=0.0001 andC=0.0004,the stable circular orbit exists; whenC >0.001 322,the stable circular orbit disappears.Furthermore,the peak of effective potential curve increases with the decrease ofC.With respect to the radius of the unstable circular orbits (runs) and stable circular orbits (rsta) onC,runsandrstaincrease asCincreases,as shown in Fig.6.Similarly,when the parametersQandbareQ1=0.7,b1=3.8;Q2=0.5,b2=3.8;Q3=0.3,b3=4.2; the corresponding parametersCwhich can make the stable circular orbits exist areC1≤0.002 205,C2≤0.002 207,C3≤0.001 323. Fig.5 The behaviors of the effective potential of particle with different C for fixed b=4.2, M =1, Q=0.7. Fig.6 The radius of the unstable circular orbit runs(a) and the radius of the stable circular orbit rsta (b)of particle with different C for fixed Q=0.7, M=1,b=4.2. Generally speaking,it is clear that there is a critical value ofbfor which the geodesic equations allow a stable circular orbit.In Fig.7,the effective potential of the particle motion with different values of angular momentumbis shown,where we fix parametersM=1,Q=0.7,C=0.On the one hand,We can find that (i) In the case ofb>3.447 102(such asb=4.2),there are two extreme points corresponding to two circular orbits.One of them is unstable circular orbit and the other is stable circular orbit. (ii) In the case ofb=3.447 102,the local maximum and minimum of the effective potential curve merge into one inflection,which corresponds to the innermost stable circular orbit occurring atr=5.891 429. (iii) In the case ofb <3.447 102 (such asb=3.0),the local minimum point of curve disappear,that is,no stable circular orbits exist.Because the angular momentum is too small for a test particle to make circular orbital motion at this time. (iv) Furthermore,asbincreases,the radius of the unstable circular orbits decrease,while the radius of the stable circular orbits increase,as seen more explicitly in Fig.8. Fig.7 The behaviors of the effective potential of particle with different b for fixed C =0, M =1, Q=0.7. Fig.8 The radius of the unstable circular orbit runs(a) and the radius of the stable circular orbit rsta (b) of particle with different b for fixed Q=0.7, M =1, C =0. On the other hand,the results obtained indicate that (v) Ifb ≤3.977 766,the maximum values of the curve are less than or equal to 1.When a test particle in an unstable circular orbits is subject to any disturbance,it either falls into the black hole or enters into bound orbits.In other word,the orbital types of test particle have absorb orbits,bound orbits and circular orbits,including stable circular orbits and unstable circular orbits. (vi) Ifb>3.977 766,the maximum value of the curve is greater than 1,which shows that when the test particle moves on an unstable circular orbit,once it is subject to any disturbance,it may fall into the black hole or escape to infinity.This indicates that the orbital types of test particle have absorb orbits,bound orbits,circular orbits,and escape orbits. In Fig.9 the effective potential of the particle motion with different values of angular momentumbis shown,where we fix parametersM=1,Q=0.7,C=0.0002.We can find that Fig.9 The behaviors of the effective potential of particle with different b for fixed C =0.0002,M =1,Q=0.7. (i) Whenb=3.443 113,the curve has an inflection point,which corresponds to the innermost stable circular orbit with the radiusrNon-Q=5.912 654.Similarly,the innermost stable circular orbit radius of the Schwarzschild black hole isrSch=6 whenIt is clearly indicate that the innermost stable circular orbit:rNon-Q< rSch.Whenb=6.392 578,the curve also has an inflection point,which corresponds to the outermost stable circular orbit with the radiusr=56.745 933.In both cases,orbital types of motion do not include bound orbits,and only include circular orbits,escape orbits and absorb orbits. (ii) When 3.443 113 (iii) Asbincreases,the location of the potential barrier maximum value moves to ther-axis left,while its location of minimum value moves to ther-axis right,that is,the radius of the unstable circular orbit decreases,while the radius of the stable circular orbit increases,as shown in Fig.10. Fig.10 The radius of the unstable circular orbit runs(a) and the radius of the stable circular orbit rsta (b)of particle with different b for fixed Q=0.7, M=1,C =0.0002. From the above discussion,we can see that quintessence has an impact on the types and stability of orbits.If there is no quintessence: whenr →∞,thenV2eff tends to 1.Atb >3.977 766,there are escape orbits.Whenb ≥3.447 102,there are bound orbits,and in this interval,stable circular orbits appear,and the innermost stable circular orbit occurring atr=5.891 429.If there is quintessence: whenr →∞,thentends to infinity.Regardless of the value ofb,the escape orbits exist.When 3.443 113≤b ≤6.392 578,there are bound orbits,and within this range,there are stable circular orbits,and the radii of the innermost and outermost stable circular orbit arer=5.912 654 andr=56.745 933,respectively.Similarly,when the parametersQandCareQ1=0.5,C1=0.001;Q2=0.5,C2=0.0005;Q3=0.7,C3=0.0005; the corresponding parametersCwhich can make the stable circular orbits exist are 3.436810≤b1≤4.451 531,3.447 618≤b2≤5.178 742,3.437 019≤b3≤5.178 666. We assume the test particle initial state is to fly towards the black hole.In Fig.11,from the analyze of the previous subsections,it is shown that when the parameters take the appropriate values,the orbital types will include stable circular orbits and bound orbits.From Fig.11(a),it can be concluded that although the values of each parameter are different,their effective potential behavior curves are very similar.That is to say,their orbital analyze is similar.Therefore,without loss of generality,we take parameterM=1,Q=0.7,b=4.2,C=0.0002 as an example (as seen in Fig.11(b)) to make a detailed analyze.We can draw some conclusions as follows: (i) In the case ofE2(such asE2==1.07),the test particle will be swallowed by black hole starting from a finite distance. (ii) In the case ofE2==1.058 155,the test particle may orbit on unstable circular orbit atrF=3.728 386,when the particle is disturbed,it may fall into black holes or escape to infinity. (iii) In the case of(such asE2==1.02),the test particle may have a escape orbit,it moves to point D from infinity,then they will deflect and fly toward infinity. Fig.11 (a) The behaviors of the effective potential of particle with different energy levels for fixed different parameters.Line 1 represents C=0.0005, b=4.2, M=1, Q=0.3; Line 2 represents C=0.0002, b=4.2,M=1, Q=0.7; Line 3 represents C=0.0008, b=3.8, M=1, Q=0.5; Line 4 represents C=0.0015, b=3.8,M =1, Q=0.5.(b) The behaviors of the effective potential of the test particle with different energy levels when we fix M =1, Q=0.7, b=4.2, C =0.0002. (iv) In the case of(such asE2==0.95),the test particle presents a bounded orbital motion betweenrB=8.445 032 (aphelion distances) andrC=35.997 248 (perihelion distances),respectively.On the left side of the barrier,the particle may fall into the black hole.On the right side of the barrier,the particle may escape to infinity. (v) In the case ofE2==0.931 246,the test particle will move on a stable circular orbit with radiusrA=14.173 833. (vi) In the case ofE2,the test particle may be wallowed by black hole or escape to infinity. In the case of null geodesics,we have thatL=0,Eq.(8) can be rewritten as follows: From Eq.(17),one can plot the behaviors of the effective potential of photon with differentQvalues for fixedb=4.2,M=1,C=0.0002 as shown in Fig.12.It is easy to find that for any values ofQ,the effective potential only has one maximum value.AsQincreases,the effective potential barrier decreases and its position moves in the direction of increasingr,which means that the radius of the unstable circular orbit increases,as seen more explicitly in Fig.13.At this time,the value of the intersection of the effective potential curve and ther-axis also increases,that is,the corresponding horizon radius is increasing.In this case,the radius of the unstable circular orbit in Schwarzschild and Schwarzschild solution surrounded by quintessence (Sch-Q) are 3.000 000,3.000 901,respectively.Comparing the radius of circular orbit under three spacetime conditions,we can see that for the radius of unstable circular orbit:rSch-Q>rSch>rNon-Q. Fig.12 The behaviors of the effective potential of photon with different Q values for fixed b=4.2, M=1,C =0.0002. Fig.13 The radius of the unstable circular orbits of photon runs with different Q values for fixed b=4.2,M =1, C =0.0002. From Fig.14 we can know that no matter how muchCis taken,the effective potential barrier has only one maximum value.In other words,only the unstable circular orbits exist.The peak value of effective potential barrier gets higher withbincreasing.Moreover,one can conclude from Fig.15 that asCincreases,the radius of the unstable circular orbit increases. Fig.14 The behaviors of the effective potential of photon with different C for fixed b=4.2, M =1, Q=0.7. Fig.15 The radius of the unstable circular orbits of photon runs with different C values for fixed b=4.2,M =1, Q=0.7. It can be clearly seen from Fig.16 that the change ofbis only related to the maximum value of the effective potential.Whenbis larger and larger,the maximum value of the effective potential also becomes larger,but the correspondingr=2.918 581 remains unchanged,that is,the change ofbdoes not affect the radius of the unstable circular orbits. Fig.16 The behaviors of the effective potential of photon with different b values for fixed C=0.0002, M=1,Q=0.7. Based on the previous analyze of the parameters and Fig.17(a),it is obvious that the shape of the effective potential behavior curve will not change significantly regardless of the values of these parameters.Therefore,without loss of generality,we take the appropriate range(C=0.0002,b=4.2,M=1,Q=0.7) as an example(Fig.17(b)) to analyze the influence of different energy levels on photon motion. In Fig.17,we assume the test photon initial state is to fly towards the black hole.Then we can obtain the following conclusions: (i) WhenE2== 0.4,the test photon with sufficient energy on the left side of the effective potential barrier may fall into the black hole,while the test photon on the right side of the effective potential barrier will escape to infinity. (ii) WhenE2==0.669 884,the test photon with sufficient energy may orbit on an unstable circular orbit with radiusr=2.951 072.When a photon is disturbed,the photon may fall into the black hole or escape to infinity. (iii) WhenE2==0.7,the test photon may fall into the black hole. Fig.17 (a) The behaviors of the effective potential of photon with different energy levels for fixed different parameters.Line 1 represents C=0.0005, b=4.2, M=1, Q=0.3; Line 2 represents C=0.0002, b=4.2,M=1, Q=0.7; Line 3 represents C=0.0008, b=3.8, M=1, Q=0.5; Line 4 represents C=0.0015, b=4.0,M=1, Q=0.5.(b) The behaviors of the effective potential of photon with different energy levels for fixed C =0.0002, b=4.2, M =1, Q=0.7. We have discussed geodesic motion in the spacetime of the non-linear magnetic charged black hole surrounded by quintessence.By varying the Lagrangian corresponding to the metric,the orbital motion equation has been obtained.It is concluded that the behavior curves of non-linear magnetic charged black hole surrounded by quintessence spacetime and de-Sitter geometry are very similar asQ/r ≫1,but whenQ/r ≪1,the behavior of the effective potential of particle in non-linear magnetic charged black hole surrounded by quintessence is similar to a Schwarzschild black hole surrounded by quintessence.Then,the effects of the magnetic chargeQ,positive normalization factorC,angular momentumband energyEon the effective potential behavior are discussed detailed from the view of time-like and null.From the effective potential behavior curves of different parameters with different values,we can see that when we consider the existence of stable circular orbits and bound orbits,although different parameters take different values,the shape of the effective potential behavior curve is similar,that is,the analysis of the effective potential behavior is similar,so we take a set of specific values as an example to illustrate.From the perspective of magnetic chargeQ,whether it is time-like or null orbital motion,the parameterQhas a similar effect on unstable circular radius,that is,asQincreases,the unstable circular radius increases.At the same time,the value of the intersection of the curve and ther-axis is decreasing.But for the time-like orbital motion,asQincreases,the stable circular radius decreases. For time-like orbital motion,we fixedM=1,Q=0.7.If there is no quintessence (C=0): the escape orbits only appear atb >3.977 766 and the bound orbits only occur atb ≥3.447 012.The radius of the innermost stable circular orbitr=5.891 429.If there is quintessence(C ̸= 0): the escape orbits always exist regardless ofbvalues.The interval in which the bound orbits exist is 3.443 113≤b ≤6.392 578.The radius of the innermost stable circular orbit and outermost stable circular orbit arer=5.912 654,r=56.745 933,respectively.It is obvious that quintessence not only affects the types and stability of orbits,but also leads to an increase in the radius of the innermost stable circular orbit.Compared with the innermost stable circular orbit radius of the Schwarzschild black hole,it clearly indicates thatrNon-Q As for the different energy levels to the types of orbit forb=4.2,C=0.0002,M=1,Q=0.7.We assume the test particle initial state is to fly towards the black hole.For time-like orbital motion,due to the different energy levels,the orbital types include absorb orbits,bound orbits,escape orbits,and circular orbits.Unstable circular orbit occur atrF=3.768 282 (E2==1.055 286),stable circular orbit occur atrA=14.169 618(E2==0.931 239),and the bounded orbital motion shows between aphelion distances (rB=8.438 773)and perihelion distances (rC=35.997 482),respectively(at this timeE2==0.95).For null orbital motion,there are only unstable circular orbit which occur atr=2.951 072 (E2==0.4),absorb orbits and escape orbits,but no stable circular orbits and bound orbits.3 Time-Like Orbital Motion
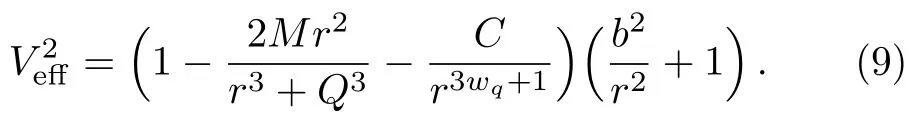
3.1 Magnetic Charge Q
3.2 Positive Normalization Factor C
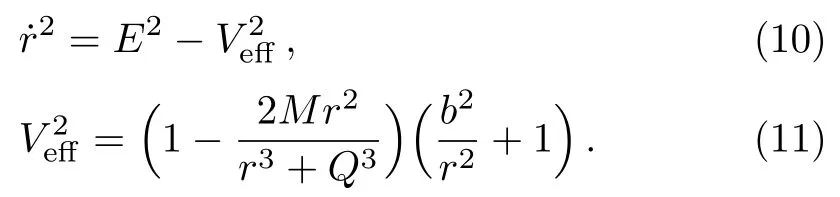





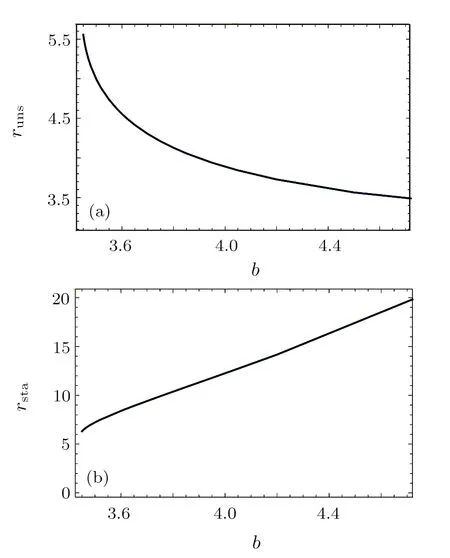
3.3 Angular momentum b

3.4 Energy Levels E

4 Null Orbital Motion

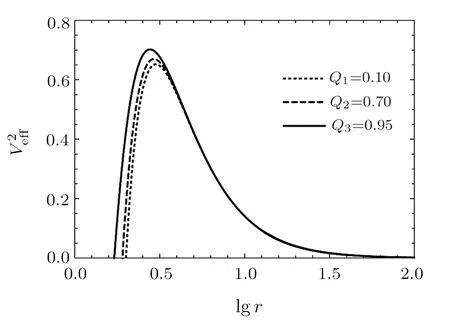
4.1 Magnetic Charge Q

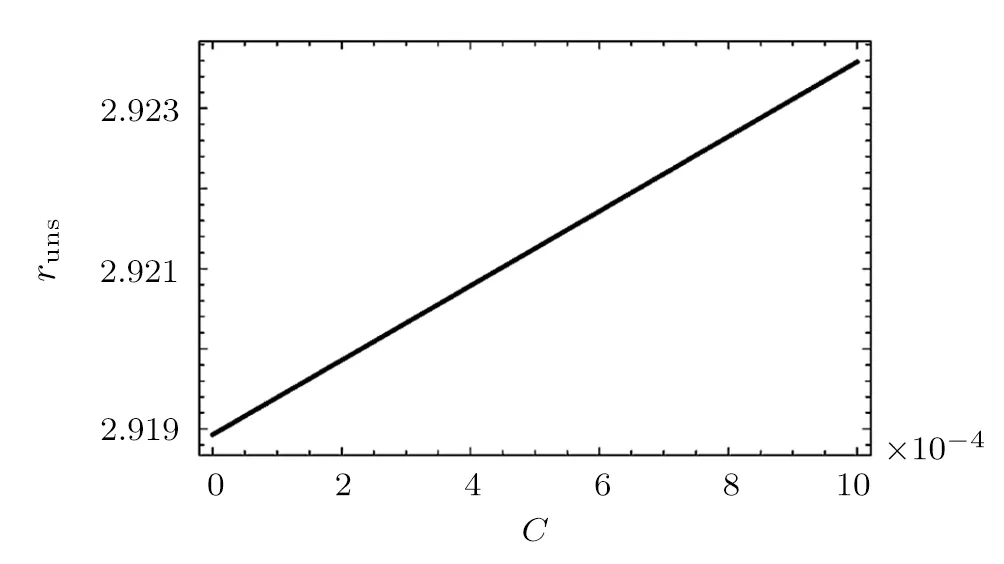
4.2 Positive Normalization Factor C

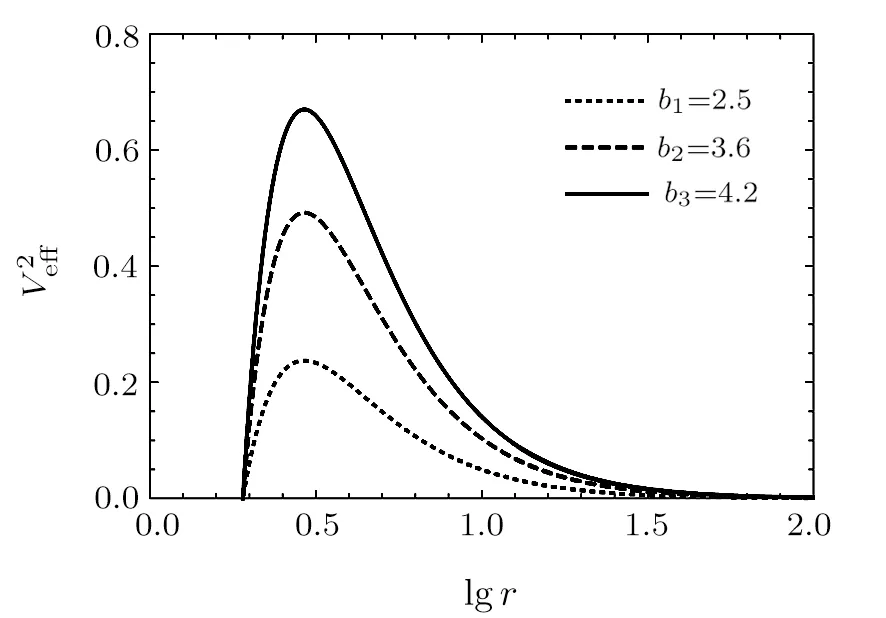
4.3 Angular Momentum b
4.4 Energy Levels E

5 Conclusions
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Superstatistics of Modified Rosen-Morse Potential with Dirac Delta and Uniform Distributions
- Design of Tunable Devices at Terahertz Frequencies Based on Quasi-Photonic Crystals Incorporated with Graphene
- Coupling Instability of a Warm Relativistic Electron Beam with Ion-Channel Guiding
- Modeling of Neurodegenerative Diseases Using Discrete Chaotic Systems
- Gravitational Deflection of Massive Particles by a Schwarzschild Black Hole in Radiation Gauge∗
- Magnetic Properties of an Antiferromagnetic Spin-1/2 XYZ Model in the Presence of Different Magnetic Fields: Finite-Size Effects of Inhomogeneity Property∗
