Robin边界条件下非线性算子方程的变号解

张强

Robin边界条件下非线性算子方程的变号解

张强

潍坊科技学院通识学院, 山东 潍坊 262700

为探索在Robin边界条件下非线性算子方程变号解，本文通过非线性算子方程变号解的稳定性分析，寻找变号解的对称广义中心平衡点，建立Jacobi数学模型进行稳定谱特征点检测，并在Dirichlet边值条件下进行奇异特征解分析，采用扰动加权方法进行Robin边界条件下非线性算子方程的临界稳态性分析，证明其约束泛函临界值的存在性和稳定性。建立非线性算子方程Caffarelli-Kohn-Nirenberg变号约束相关性条件，计算非线性算子方程的变号解满足的边界条件，构建Robin边界条件下Sobolev和Hardy临界扩展约束算法，实现对非线性算子方程变号解准确计算和渐进稳定性证明。

Robin边界条件; 非线性算子方程; 变号解

非线性方程广泛用于描述非线性动力学模型和物理学模型，Robin边界条件下非线性算子方程对于实际的控制数学和应用数学具有很好的描述，在Robin边界条件约束下分析非线性算子方程的变号解，根据变号解的稳定性进行控制系统的收敛性约束分析，Robin边界条件非线性算子方程的解不论是对于理论的数学分析，还是实际的数学应用来说都具有重要的意义[1]。Robin边界条件非线性算子方程中的解具有变号性，受到符号约束的稳态特性的影响，导致方程的解向量存在稳态误差，在Robin边界条件下无法解出正确的变号解。

对此，本文研究一种优化的Robin边界条件下非线性算子方程变号解分析方法[2]，在某些不确定的条件下，根据Robin边界条件下非线性算子方程变号解的发散特征量，进行约束性关联分析，采用稳态特征收敛模型计算Robin边界条件下非线性算子方程变号解的稳定性，结合判决和门限准则，在Dirichlet边值条件下进行非线性算子方程的奇异特征解分析，采用扰动加权方法进行Robin边界条件下非线性算子方程的临界稳态性分析，采用马尔尼数链随机分析模型，进行边界收敛性判断，求得Robin边界条件下非线性算子方程的变号解，建立非线性算子方程Caffarelli-Kohn-Nirenberg变号约束相关性条件，计算非线性算子方程的变号解满足的边界条件[3]，构建Robin边界条件下Sobolev和Hardy临界扩展约束算法，实现对非线性算子方程变号解准确计算和渐进稳定性证明。经过Robin边界条件使得目标函数收敛于最优解，论文从理论和数学推导上进行和变号解的稳定性和有限收敛性验证。

1 非线性算子方程数学模型构建与问题描述

1.1 非线性算子方程数学模型及引理

在非线性微分方程发展的过程中，需要分析Robin边界条件下非线性算子方程的变号解，结合变号解的稳定性和收敛性进行非线性动力学分析，建立稳态收敛的数学控制模型[4]，并应用在动力学控制中，定义Robin边界条件非线性微分方程的正多解：→R的>0阶Dirichlet边值特征解向量为：

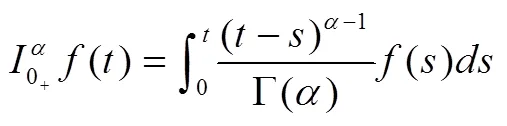
存在非齐次边界条件下[6]，有唯一变号解：

其中：为非线性算子方程中变号解取得的整数值，取值要求为大于或等于的整数，使得方程具有广义随机收敛性[7]。

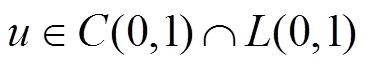
1.2 Robin边界约束条件

在Jacobi数学模型中进行非线性算子方程的稳定谱特征点检测，在Dirichlet边值条件下进行非线性算子方程的奇异特征解分析[9]。

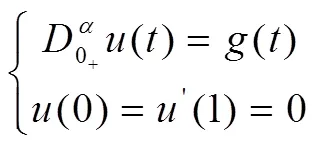
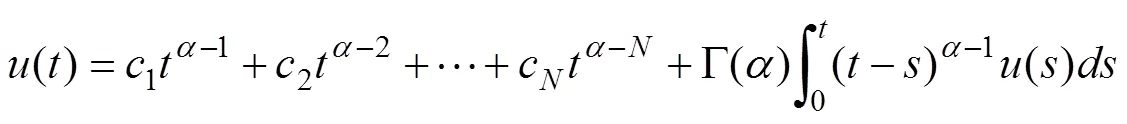
且：

综上分析，采用扰动加权方法进行Robin边界条件下非线性算子方程的临界稳态性分析，求得方程的变号解，结合非线性算子方程的变号解分析结果进行稳态收敛性证明。

2 非线性算子方程的变号解及稳定性分析

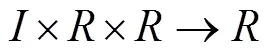
证明

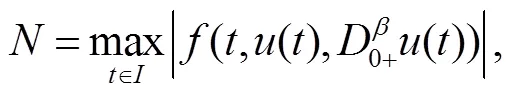
结合约束性关联分析，在Robin边界条件下非线性算子方程的联合有界特征量为：

从而可以推导得到：

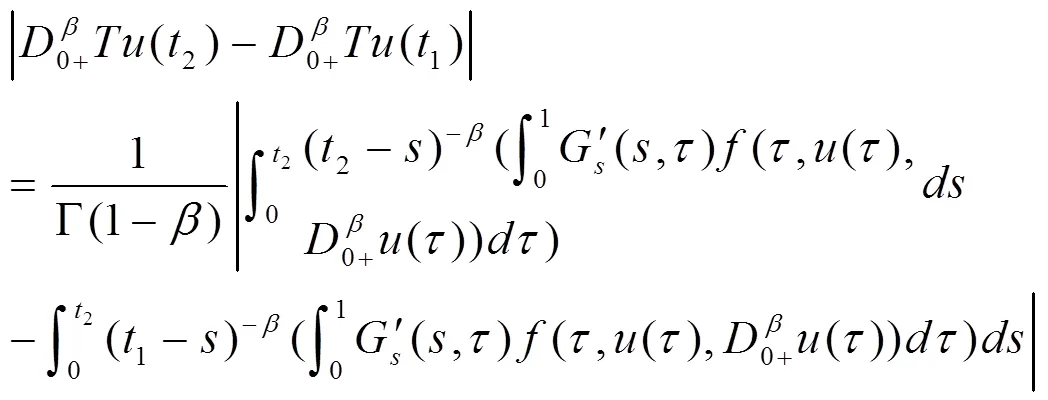
通过建立非线性算子方程Caffarelli-Kohn-Nirenberg变号约束相关性条件，得到如下结论：

可见，计算得到的Robin边界条件下非线性算子方程变号解是稳态收敛，命题得证。

3 数值分析

通过数值分析的方法测试Robin边界条件下非线性算子方程变号解分析问题，采用SPSS14.0作为分析软件，进行数值分析，数值样本采样随机序列样本，样本数据的规模为2000，测试集为200，训练集为100，迭代次数为1024，根据上述测试参数设定，进行非线性算子方程变号解分析，得到测试样本数据见表1。

表1 测试样本数据

将上述测试数据通过最小二乘拟合方法输入到系统中，分析Robin边界条件下非线性算子方程变号解问题，使用传统方法分析用得到结果如表2描述。

表2 传统算法分析数据

使用本文算法分析Robin边界条件下非线性算子方程变号解参数用表3描述：

表3 本文算法分析数据

分析上述测试结果得知，本文方法进行Robin边界条件下非线性算子方程变号解分析的拟合效果较好，收敛性较强，并应用在控制系统中，得到控制性能曲线对比如图1所示，分析图1得知，本文方法进行Robin边界条件下非线性算子方程变号解优化求解，提高了收敛性和全局稳定性。

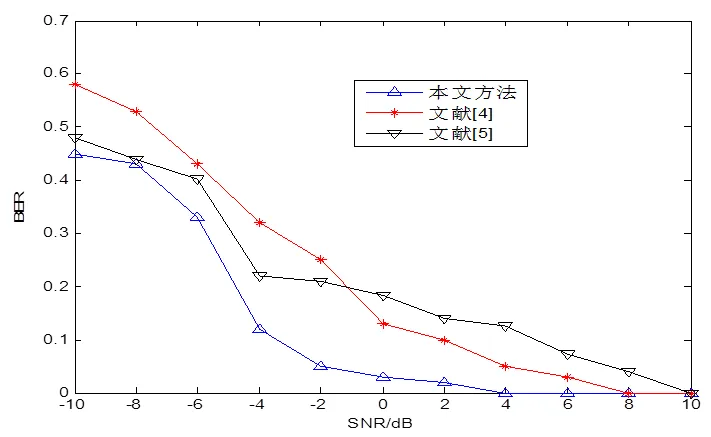
图1 性能对比

4 结语

本文研究在Robin边界条件下非线性算子方程变号解问题，结合非线性算子方程变号解的稳定性分析，提高非线性控制系统的稳定性。计算非线性算子方程变号解在对称广义中心的稳定性平衡点，建立Jacobi数学模型进行非线性算子方程的稳定谱特征点检测，在Dirichlet边值条件下进行非线性算子方程的奇异特征解分析，采用扰动加权方法进行Robin边界条件下非线性算子方程的临界稳态性分析，证明非线性算子方程的约束泛函临界值的存在性和稳定性，建立非线性算子方程Caffarelli-Kohn-Nirenberg变号约束相关性条件，计算非线性算子方程的变号解满足的边界条件，构建Robin边界条件下Sobolev和Hardy临界扩展约束算法，实现对非线性算子方程变号解准确计算和渐进稳定性证明。本文方法对非线性算子方程变号解分析的拟合效果较好，收敛性较强。

[1] 李盼晓.非局部时滞反应扩散方程波前解的指数稳定性[J].应用数学和力学,2018,39(11):1300-1312

[2] 李远飞.Robin边界条件下更一般化的非线性抛物问题全局解的存在性[J].应用数学学报,2018,41(2):257-267

[3] Wang X. Green functions for a decagonal quasicrystalline material with a parabolice boundary[J]. Acta Mechanica Solida Sinica, 2005,18(1):57-62

[4] Liu Y, Luo SH, Ye YH. Blow-up phenomena for a parabolic problem with a gradient nonlinearity under nonlinear boundary conditions[J]. Computers and Mathematics with Applications, 2013,65:1194-1199

[5] 都琳,张莹,胡高歌,等.一种双寡头垄断Cournot-Puu模型的混沌控制研究[J].应用数学和力学,2017,38(2):224-232

Sign Variation Solution of Nonlinear Operator Equation under Robin Boundary Condition

ZHANG Qiang

262700,

To explore the sign variation solution of nonlinear operator equation, this paper established Jacobi mathematical model to look for an equilibrium point of symmetric generalized center of the variable sign solution, the Jacobi model was established to detect the stability spectrum characteristic point of nonlinear operator equation and The singular characteristic solution of nonlinear operator equation was analyzed under Dirichlet boundary value condition, and the critical steady-state of nonlinear operator equation with Robin boundary condition was analyzed by perturbation weighting method. This paper proved the existence and stability of the critical value of constrained functional of nonlinear operator equations, established the constraint correlation conditions of nonlinear operator equations with Caffarelli-Kohn-Nirenberg variation sign, and calculated the boundary conditions satisfied by the variation solutions of nonlinear operator equations. The critical extended constraint algorithms of Sobolev and Hardy under Robin boundary conditions were constructed, and the exact calculation of the signed solutions of nonlinear operator equations and the proof of asymptotic stability were realized.

Robin boundary condition; nonlinear operator equation; sign change solution

O211.62

A

1000-2324(2019)05-0893-05

10.3969/j.issn.1000-2324.2019.05.035

2018-06-04

2018-10-12

山东省教育科学“十二五规划”高等教育数学专项课题(CBS15001)

张强(1980-),男,硕士,讲师,研究方向为计算数学. E-mail:zhangqiang55@126.com