地形起伏条件下页岩气管网布局优化研究
2019-11-07董建蓉
张 禾,周 军,董建蓉,马 骐,周 轩
(1.中国石化川气东送天然气销售中心,湖北 武汉 430200;2.西南石油大学,四川 成都 610500;3.中国石油四川销售分公司,四川 成都 610017)
0 引 言
目前,页岩气在中国处于快速发展时期,页岩气具有井分布广、单井产量低、井口节流后压力高、生产初期压降快和生产周期长等特点,如何减少地面建设投资,降低运营成本,实现经济效益最大化,是页岩气地面建设的重点研究工作[1-2]。页岩气集输通常包括放射状、枝状、环状及组合型4种管网拓扑类型。页岩气管网的形式多样:比如针对中国焦石坝区块平台分布分散,区块面积南北长、东西窄等特点,采用环状-支状管网;美国Haynesville页岩盆地采用枝状管网,美国北达科他州Bakken页岩气田采用放射状管网,美国的Barnett页岩气田和Marcellus页岩气田等采用环状管网布置形式,Barnett页岩气田采用辐射-树枝形集气管网将井场来气集中输至处理厂进行脱水后外输。
页岩气集输管网布局优化是复杂的混合整数非线性优化问题,大量子问题为非确定性多项式难题,其优化求解困难。ZHOU等[3-5]对常规气田和煤层气管网布局优化进行了研究。DROUVEN[6]研究了页岩气管网压力分布优化问题,在页岩气管网布局研究方面,梁霄等[7-8]提出了两级放射状的布局方案,并做了对比分析,但未考虑地形起伏的影响。任玉鸿等[9]采用分级优化方法,讨论了多种管网结构的页岩气管网平面布局。房东等[10]开展了地形起伏条件下的页岩气单条管道路径优化。目前,页岩气集输管网系统的规划方案主要是进行二维平面设计,对于起伏地形并未进行系统考虑,精度差。另外,部分设计考虑了高程,但是并未对高程进行精细处理。集输管网规划设计主要仍基于递阶优化思路,采用分级优化,对井组择优归集划分、集气站站址优选、干支管网连接方式和管网结构参数的优化4个子问题逐一求解[11-12],在优化过程中仅是局部最优解,系统性差。
中国页岩气富集区多处山地,地形复杂,开发难度大,单一形式的地面集输管网无法实现高效低成本开发的目的,需采取组合型管网布置方式,考虑地形起伏下的页岩气组合管网整体布局优化,对提高页岩气田经济效益,促进页岩气产业发展具有重要的研究意义。
1 页岩气管网布局优化策略
针对页岩气组合管网优化精度差、系统性差等问题,将井组最优划分和站址优化看作整体进行优化,同时在干支管网连接方式确定后,引入管道路径优化,对路径起伏程度较大管道进行路径优化。
2 井组划分与集气站站址整体优化
以达到方案经济性最优为原则,对枝-枝状页岩气管网的管道、集气站建设费用建立目标函数,采用遗传算法进行求解。
2.1 井组划分与站址优化模型
集气管道的一次投资费用与管道长度、管径有关,对于某条由i井到j集气站的管道,其投资费用为:
(1)
(2)
(3)
λ=α/β
(4)
(5)
式中:K表示费用系数;K1、K2、α、β、λ为系数,均可基于数据资料采用最小二乘法进行回归;Cij为管道ij的投资费用,104元;Lij为该管道的三维长度,m;Dij为该管道的直径,mm;(xi,yi,zi)、(xj,yj,zj)为井i和集气站j的位置坐标;Qij为管道输气量,m3/d。
用Cj表示集气站一次投资费用,104元。综上,井组划分与站址整体优化目标函数C表示为:
(6)
式中:C表示目标函数值,104元;n、m分别为气井与集气站数量;Aij表示井i和集气站j的连接关系,连接时取1,否则为0。
约束条件包括井站隶属关系唯一性约束、集输半径约束、最小管辖井数与最小站场处理量约束,约束表达式如下:
(7)
(8)
LijAij≤R
(9)
(10)
Qj≥Qmin
(11)
(12)
式中:R为集输半径,km;Qj为j号集气站处理量,m3/d;Qmin为集气站最小处理量,m3/d;Nmin为集气站最小管辖井数。
2.2 井组划分与站址优化求解
遗传算法(Genetic Algorithm,GA)是一种基于自然选择和基因遗传学原理的随机并行搜索算法,其本质是一种求解问题的高效、并行、全局的搜索方法[13]。同传统的优化算法相比,GA具有更好的并行处理能力、良好的鲁棒性和柔韧性[14-18]。 通过染色体编码,种群初始化,适应度函数设计,基因选择、交差、变异,算法控制参数设定以及约束条件处理,得到优化结果。采用轮盘赌选择,精英个体保留策略,自适应交叉概率调节机制,引入罚函数以降低不满足约束条件的个体适应度并将其淘汰,提高遗传算法搜索过程中的搜索速度,避免进入下一代进化而导致搜索时间延长。
3 干支管网连接方式优化
3.1 连接方式优化模型及求解算法
在干支管网连接优化中,采用管道投资费用作为目标函数,优化模型为:
(13)
求解枝-枝状管网连接问题实质上是求解最小生成树(Minimum Spanning Tree,MST)问题,因而采用Kruskal算法[19]进行求解。
3.2 页岩气管网初步连接判断
集输管网井组内的气井可以任意两两相连,并不存在天然的管网初步连接,若有n口气井,则会产生(n-1)+(n-2)+…+2+1种连接方式,剔除没有实际工程意义的,减小计算量,避免不合理的方案产生[20]。如图1所示,4为集气站,其余为气井,两两连接共有21条可选边数,由于1—4之间可以通过1—3—4连接,去除图中1—4、2—5、4—7、6—7不合理的的方案。

图1 管网不合理连接示意图
拟定管网初步连接判断机制:所有气井两两连接,在该管线附近定义一个长方形,长方形的边通过2口气井,且气井为长方形边的中点,长方形的宽为2γ×lij,γ为定义AD距离的一半与AB距离的百分比,如图2所示。若长方形区域内存在其他点,则取消该管线连接,若不存在,则保留原连接。

图2 定义长方形示意图
4 起伏管道路径寻优
在指定管道起点(X1,Y1,Z1)、终点位置(Xn,Yn,Zn)的前提下,由于管道起点压力、输气量已定,因此,不同路径方案管道投资、施工费用均只与管道长度相关,由此以管道总长度为目标函数,在三维地形下管道总长度表示为:
(14)
式中:L为管道总长度,m;Xi、Yi、Zi为离散的坐标。
A*(A-star)算法是求解最短路径最有效的直接搜索方法之一,也是解决众多搜索问题的常用启发式算法,距离估算值与实际值越接近,最终搜索速度越快。此次研究中路径寻优采用A*算法进行求解。
5 实例分析
某区块现有气井72口,将各气井坐标导入Global Mapper软件中,采用改进后的遗传算法利用Matlab2013b进行求解,确定井组划分与站址位置。对划分好的井组进行初步连接,以井组1为例,井组1共有15口气井(含集气站),若气井两两相连,则会产生105条连接管道,经管网初步连接判定,满足要求的共有28条管道,简化效果明显,得到简化后的初步连接如图3所示,图中自线为初步管道。利用Kruskal算法对各井组采气管网初步连接图以及集气站间集气管网初步连接图进行优化,得到各井组连接方式如图4所示。

图3 井组1采气管网初步连接

图4 页岩气管网整体布局
利用Kruskal算法优化得到的管网布局,计算得到部分管道起伏程度较大,路径最大边坡达到了48.73 °,这是传统二维平面设计的缺陷,并未系统考虑起伏地形,设计出的管道起伏程度较大,难以符合真实环境。因此,利用A*算法对管道路径最大边坡大于30.00 °管道进行优化。以集气站3至集气站5的管道为例,提取6 000 m×10 000 m地形数据,分辨率为20 m,共提取数据点300×500,共15×104个。优化后管道路径与原路径起伏程度对比如图5所示。

图53D视图下集气站5至集气站3管道原路径(紫)与优化路径(橙)
优化前后集气管道(集气站5至集气站3)参数对比如表1所示,优化后路径最大边坡低于30.00 °,同时最大高程降低14.48%,有效降低路径最大高差,管道三维长度缩短54 m。与原方案对比,优化后的管网三维长度比原方案有所缩短,具体参数见表2。

表1 路径优化前后集气管道参数对比
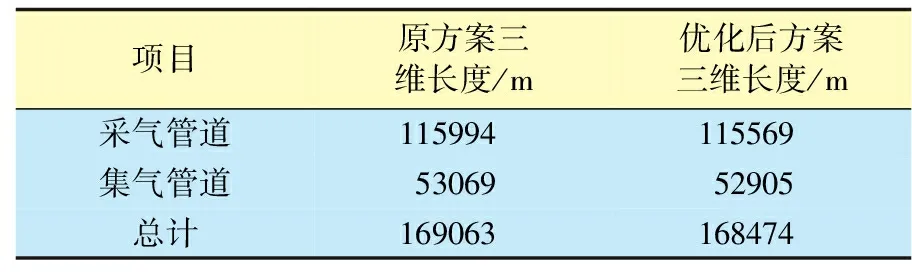
表2 原方案与优化后方案对比
6 结 论
(1) 针对页岩气枝-枝状管网布局优化,通过将传统的子问题井组划分与子问题站址优化进行整体优化,确定管道、集气站建设费用作为目标函数,以井站隶属唯一性、集输半径、最小管辖井数和最小站场处理量作为约束条件,使优化系统性得到提高。
(2) 在进行管网连接前,引入管网初步连接剔除不合理管线,采用长方形范围进行判断,能够大幅减少不合理连接,提高了优化效率和优化效果。
(3) 在干支管网连接方式基础上,采用A*算法对路径最大边坡超过30 °的管道进行路径优化,优化后的路径最大边坡能够有效控制在30.00 °以内,同时能够降低了路径最大高程,缩短了管道三维长度。
