注采井间连通裂缝参数干扰试井解释模型

2019-11-07吕亿明薛建强常莉静崔文昊苏祖波

特种油气藏 2019年5期

吕亿明，薛建强，常莉静，崔文昊，苏祖波

(1.中国石油长庆油田分公司，陕西西安 710018； 2.低渗透油气田勘探开发国家工程实验室，陕西西安 710018)

0 引言

超低渗透油藏具有储层物性差、裂缝多、渗透率低等特点[1]。裂缝是流体在超低渗透油藏中流动的主要通道[2]。裂缝通常有一个主方向，在该方向上渗透率最大，当裂缝渗透率达到一定程度之后，便会形成一条优势渗流通道[3]。干扰试井是判断井间连通情况，确定井间连通地层参数的有效测试方法[4-5]。国内外的干扰试井模型大多为直井与直井之间[6-11]，直井与水平井、水平井与水平井之间的较少[12-16]，而关于直井与压裂水平井之间裂缝连通的几乎没有。在前人研究成果[17-24]基础上，以华庆油田为例，对以多段压裂水平井(生产井)为中心，周围分布直井(注水井)所形成的注采单元进行研究，建立了注采井间连通裂缝参数干扰试井解释模型，并对该油田的目的井组进行试井解释，进而验证模型的合理性。

1 物理模型

华庆油田属于典型的超低渗透油藏，油藏开采方式主要为直井注水、水平井生产的方式。由于周围注水井的增多及注水压力升高等因素的影响，油藏中的裂缝开启程度变大、延伸长度变长；注采井间裂缝性连通明显，主要表现为采油井见效快，含水上升快，甚至出现了暴性水淹。以该油田元284区块资料为基础，建立了如下物理模型。在顶底封闭侧向无限大油藏中，考虑2口井，一口直井(OW)作为注水井(关井)，一口水平井(AW)作为生产井，2口井之间主要以裂缝形式沟通，其物理模型示意图如图1所示。基本假设条件为：①油藏水平等厚且各向异性，顶面和底面为封闭边界，外边界为无限大边界；②油藏的储层厚度为h，水平井长度为L；水平井压裂裂缝间距ΔL相等；水平井压裂裂缝关于水平井井筒对称，压裂裂缝半长hf相等及压裂裂缝完全穿透整个储层；③水平井以定产量进行生产，各条压裂裂缝的流量不一定相等，水平井井底的总流量一定；④地层岩石和流体均微可压缩，且压缩系数为常数，流体黏度不变；⑤流体在水平井和压裂裂缝内的流动均为无限导流，流体一旦流入压裂裂缝，瞬间流入井筒，且不考虑裂缝端面流体的流入量；⑥直井与水平井之间通过一条连通裂缝连通，连通裂缝包括等效裂缝和等效裂缝与水平井的相交的某一条压裂裂缝，并且等效裂缝为有限导流裂缝，即流体在等效裂缝中流动会产生压降，在等效裂缝内不同位置处所对应的压力和流量不同；⑦忽略重力、毛管力的影响，流体在地层中作等温流动；⑧直井和水平井不考虑井筒储存效应和表皮效应。

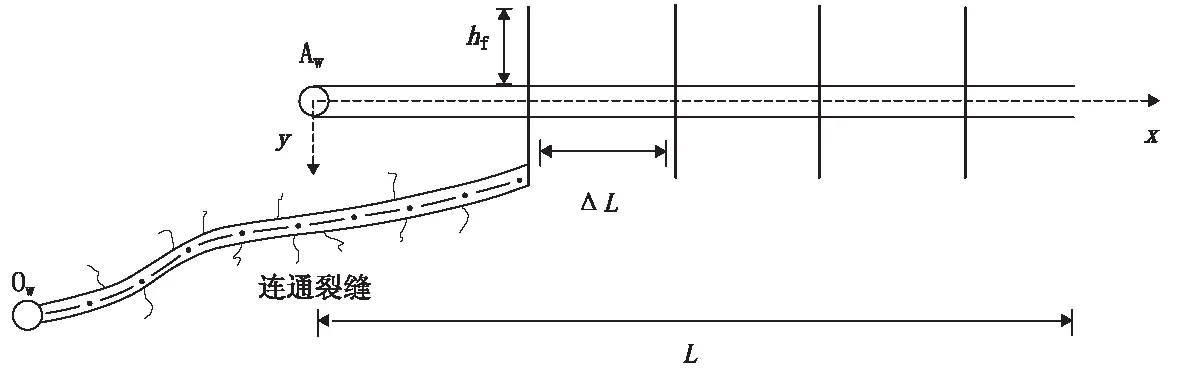
图1 注采井间连通裂缝参数干扰试井解释模型

2 数学模型

2.1 坐标变换

如图1所示，一般的多段压裂水平井模型和有限导流裂缝模型是不适用的，需要针对不同的坐标系，进行相应的坐标变换，坐标变换示意图如图2所示。在x′-y′坐标系中，设裂缝与x轴方向呈角度为θ°，由坐标旋转和坐标平移原理[28]可得：

(1)

式中：(x′，y′)为x′-y′坐标系中地层任意一点坐标； (x，y)为x-y坐标系中地层任意一点坐标；(xw，yw)为x-y坐标系中裂缝的中点坐标。

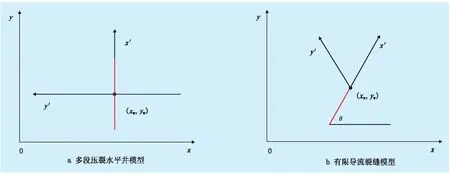
图2 坐标变换示意图

2.2 多段压裂水平井

(2)

pD=Kh[pi-p(r,t)]/(1.842×10-3qμB)

(3)

qfD=rqf/q

(4)

(5)

(6)

(7)

(8)

LfD=Lf/r

(9)

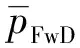
(10)

(11)

qfDi=rqfi/q

(12)

LfDi=Lfi/r

(13)

xDj=xj/r

(14)

yDj=yj/r

(15)

xwDi=xwi/r

(16)

ywDi=ywi/r

(17)

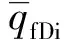
2.3 有限导流裂缝

(18)

qfD1=Lcfqf1/q

(19)

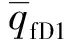
(20)

xwDk=xwk/r

(21)

ywDk=ywk/r

(22)

式中：(xwDk，ywDk)为等效裂缝与第k条压裂裂缝交点(xwk，ywk)的无因次坐标；k=1，2，…，m。

2.4 物质平衡原理

由水平井以定产量生产，依据物质平衡原理，可得：

(23)

2.5 直井井底压力

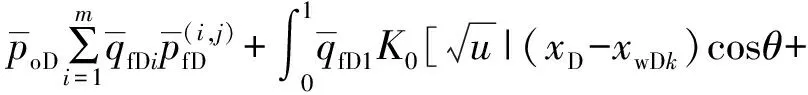
(24)

(25)

xoD=xo/r

(26)

yoD=yo/r

(27)

式中：(xoD，yoD)为直井(xo，yo)的无因次坐标。

(28)

3 模型计算结果分析

上述直井的无因次井底压力为拉式空间下的解析解，对其进行Stehfest数值反演，得到实空间的数值解，再利用数值解绘制模型的典型图版，并对渗流基本特征及参数敏感性进行分析。

3.1 渗流基本特征分析

图3为注采井间裂缝性连通干扰试井模型典型图版，典型图版曲线划分为3个主要的流动段：Ⅰ期(早期线性流)，主要受到连通裂缝的影响，表现为前期压力导数曲线的变化幅度比压力曲线变化大，后期压力曲线与压力导数曲线相交；Ⅱ期(中期流)，受到连通裂缝和水平井的共同影响，表现为出现“驼峰”或者“凹子”的特征；Ⅲ期(晚期径向流)，表现为压力导数曲线稳定在0.5水平线。

图3 注采井间裂缝性连通干扰试井模型典型图版

3.2 参数敏感性分析

图4为xoD变化图版，直井横坐标位置越靠近水平井，早期线性流阶段压力曲线越陡，中期流阶段压力导数曲线位置越靠上，表明连通裂缝的长度在变短，连通裂缝单独对直井的影响在减小，连通裂缝和水平井对直井的共同影响在增大。

图5为等效裂缝与多段压裂水平井的第mi条压裂裂缝连通的mi变化图版，主要影响早期线性流阶段和中期流阶段，随着mi变小，早期线性流阶段压力曲线变陡幅度减小，中期流阶段压力导数曲线位置越靠下，表明连通裂缝的长度变长，连通裂缝单独对直井的影响增大，连通裂缝和水平井对直井的共同影响减小。

图6为FCD变化图版，主要影响中期流阶段，随着FCD的增大，中期流阶段压力导数曲线位置先升高再降低，表明连通裂缝和水平井对直井的共同影响先增大后减小。

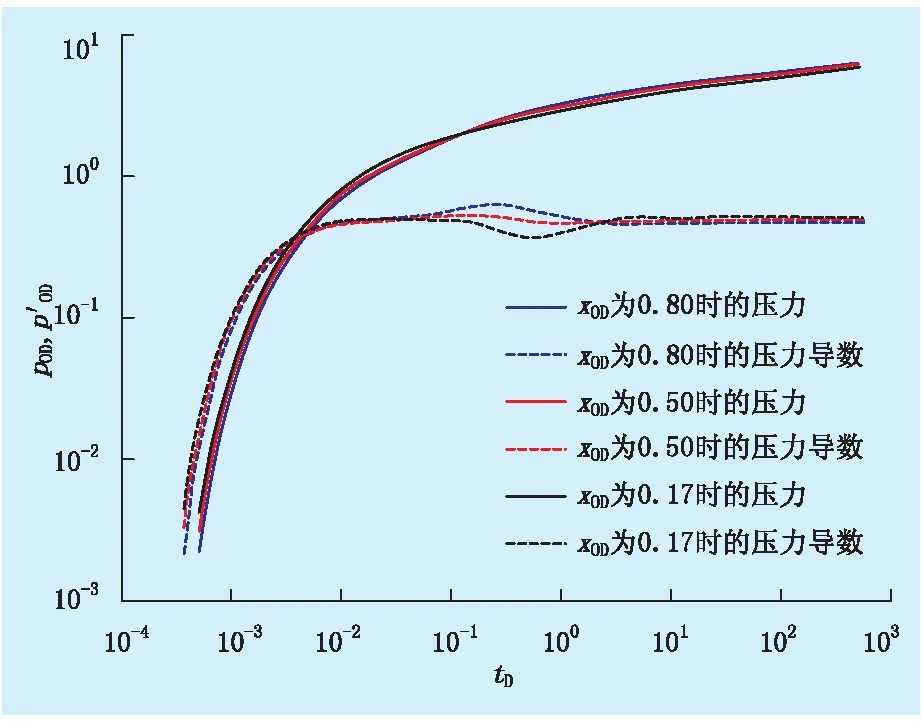
图4 xoD变化图版

图5mi变化图版

图6FCD变化图版

4 应用实例

以华庆油田元284区块的庆平A1井组为例，对本模型进行实例验证。水平井庆平A1井在干扰试井测试前已经发生暴性水淹，说明其周围存在与之裂缝性连通的注水井。该井对应注水井6口，一线注水井4口(元A1-43、元A1-41、元A1-42、元A1-45井)，二线注水井2口(元A1-39、元A1-43井)。干扰试井前，庆平A1井和周围的注水井均关井一段时间，待压力平稳后，庆平A1井以某一定产量生产，相当于给周围注水井一个压力“激动”信号，若周围存在与之连通的注水井，则会收到该激动信号。庆平A1井组激动-注水压力监测曲线如图7所示。庆平A1井激动后，仅观测井元A1-43井收到激动信号产生压力响应，而其他观测井未出现压力响应。超低渗透油藏中进行干扰试井测试，由于地层渗透率低，压力传播速度慢，干扰信号传输需要较长的时间。庆平A1井激动24 h时观测井元A1-43井产生压力响应，即可判断2口井间为裂缝性连通。庆平A1井的压裂段数为6，其中点与元A1-43井的距离为413 m，产量为30 m3/d，流体黏度为0.55 mPa·s，原油体积系数为1。对该实例进行试井解释，理论与实测压力和压力导数双对数拟合曲线。

由图8可知，曲线主要拟合了第1阶段：早期线性流阶段，即井间的连通裂缝对元A1-43井的影响。

图7 庆平A1井组激动-注水压力监测曲线

图8 元A1-43井压力和压力导数双对数拟合曲线

因为庆平A1井的激动时间为146 h，相对较短，庆平A1井通过地层对观测井的影响还未出现，所以压力和压力导数曲线没有出现第2和第3阶段。试井解释结果：元A1-43井主要与庆平A1井的第3条压裂裂缝沟通，从而确定了裂缝方向，连通裂缝长度为415 m，大于元A1-43井到庆平A1井中点的距离，无因次导流能力为8，压裂裂缝半长为20 m，地层渗透率为0.198mD。利用已建立的模型对现场进行干扰试井解释，结果与现场已知的地质数据反映的情况基本吻合，说明了解释结果的合理性。