Numerical investigation on coherent mid-infrared supercontinuum generation in chalcogenide PCFs with near-zero flattened all-normal dispersion profiles∗
2019-11-06JieHan韩杰ShengDongChang常圣东YanJiaLyu吕彦佳andYongLiu刘永
Jie Han(韩杰),Sheng-Dong Chang(常圣东),Yan-Jia Lyu(吕彦佳),and Yong Liu(刘永)
1State Key Laboratory of Electronic Thin Film and Integrated Devices,School of Optoelectronic Science and Engineering,University of Electronic Science and Technology of China,Chengdu 610054,China
2School of Environment,3480 University Street,McGill University,Montréal H3A 0E9,Canada
Keywords:supercontinuum generation,photonic crystal fiber,nonlinear optics
1.Introductio n
Coherent light sources in mid-infrared(MIR)region are of great significance for scientific and engineering applications in many domains such as medical surgery,[1]remote sensing,[2]and military countermeasure,[3]since a large number of molecules display a strong vibration absorption capability in this region. The supercontinuum(SC)generation is a process that generates a broad spectrum,promoting the applications in the relevant fields above. Silica-based glass fibers have proved to be excellent nonlinear medium for SC generation.However,the strong material absorption of silica fibers in the MIR region(>2.5µm)limits their applications at longer wavelengths. Compared with silica fibers,chalcogenide glass fibers benefit from their wide transmission window up to 20µm,[4]thus making them a superior candidate for MIR-SC generation. To date,MIR-SC generation spanning from 2µm to 16µm has been successfully demonstrated by using a chalcogenide fiber as a nonlinear medium.[5]Appropriate pump wavelength also plays a crucial role in wide SC generation.It needs to be in the anomalous dispersion regime and near the zero dispersion wavelength of the said fiber.[5]The spectral broadening is mainly dominated by soliton dynamics,especially soliton fission,and subsequent soliton selffrequency shift.However,soliton dynamics is sensitive to the input noise,[6]which causes the spectral coherence to degrade.In view of the perspective of practical applications,the SCs with high coherence possesses great applications in optical coherence tomography[7]and frequency metrology.[8]
To generate coherent SCs,fibers with all-normal dispersion profiles are now used. For SCs in these fibers,spectrum broadening is mainly dominated by self-phase modulation(SPM)and optical wave breaking(OWB),which suppress soliton-related process,especially soliton fission. The generated SC possesses perfect coherence in the entire spectrum.In the following experimental work the all-normal dispersion fibers are adopted for better SC coherence.[9–13]Al-Kadry et al.generated a 0.96-µm–2.5-µm coherent SC by using 150-pJ pulses to pump all-normal dispersion chalcogenide microwires.[9]A coherent SC covering 2.2µm–3.3µm was demonstrated by using all-normal dispersion AsSe2–As2S5microstructured fiber pumped at 2.7µm.[10]Nagasaka et al.used a double-cladding chalcogenide fiber,which has As2Se3core and AsSe2inner cladding and As2S5outer cladding,pumped with 1.3-MW pulses at 10µm to generate 2-µm–14-µm coherent SC.[11]Optical parametric amplifier(OPA)was adopted because the considered pump pulse is hard to obtain just by fiber laser. However,OPA suffers huge system and high expanse,which is disadvantageous to the practical applications. Jiao et al.generated a coherent SC covering 2µm–14µm by pumping a double-cladding tellurium fiber with femtosecond laser at 5µm.[12]The choice of the double-cladding fiber leads to the high peak power(estimated at around several megawatts)of the pump pulses.In addition,OPA was also used to provide pump pulses.Zhang et al.generated a coherent SC covering 1.7µm–12.7µm by pumping a chalcogenide tapered fiber at 5.5µm.[13]The adopted dispersion curve is inverted-V-shaped.The long wavelength components experience large group velocity dispersion,which also means that high pump power leads to a large red frequency shift.
There are also several numerical simulations on SCs in all-normal dispersion medium. Karim et al. numerically demonstrated a 2-µm–5.5-µm SC by pumping a Ge11.5As24Se64.5PCF with 5-kW pulses at 3.1 µm.[14]Then Singh Saini et al.simulated coherent SC covering 1.2µm–7.2µm by pumping a chalcogenide rib waveguide at 2.8µm.[15]Nagasaka et al.numerically generated a coherent SC covering 3.3µm–10.4µm by pumping a chalcogenide double-clad fiber with 300-fs pulses at 6µm.[16]The considered pump pulses are still based on OPA.Diouf et al.numerically generated a coherent SC covering 2.9µm–4.575µm by pumping an As38.8Se61.2PCF with 50-fs pulses at 3.7µm.[17]The adopted dispersion curve is also inverted-V-shaped,which is disadvantageous to increasing red frequency shift due to the large dispersion of long wavelength components.[18]Cherif et al.generated a 2µm–8µm coherent SC by pumping an As2Se3-based PCF with pulses at 5µm.[19]The adopted dispersion curve is inverted-V-shaped,and the pump pulse is hard to obtain by fiber laser.
Appropriate all-normal dispersion profile is significant for the broadband coherent SC generation. Compared with the inverted-V-shaped dispersion curve,an inverted-L-shaped dispersion curve is very beneficial to increasing red frequency shift of the SC.[18]To obtain such inverted-V-shaped dispersion characteristics,fibers with high design flexibility are more attractive. Having high design flexibility and being able to achieve the desired dispersion characteristics,the photonic crystal fibers(PCFs)enjoy the dispersion curve that is changeable by varying the geometric parameters,and the nonlinearity of PCF can also increase due to the enhanced confinement of the optical field.All the above merits of PCFs are favorable for generating broadband SC in the MIR region.
In this paper,we design a novel 3-cm-long As2Se3–As2S5PCF with near-zero flattened all-normal dispersion profiles.With the above all-normal dispersion PCF,it is possible to generate SC up to 10µm with perfect coherence when pumped with pulses at 3µm,and the resulting SC is able to cover two atmospheric windows of 3µm–5µm and 8µm–10µm wavelengths.Our simulations provide a potential all-fiber scheme to obtain highly coherent MIR-SC.
2.Numerical model
Pulse propagation in the fiber can be modeled by generalized nonlinear Schrödinger equation(GNLSE).Based on the derivation of GNLSE in Ref.[20],we solved this equation in the frequency domain:

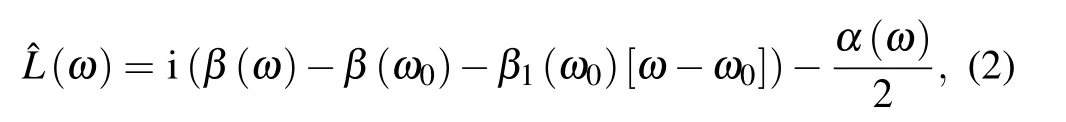
where α(ω)denotes the frequency-dependent linear loss in the fiber, β(ω)the propagation constant, ω the angular frequency,ω0the central angular frequency,andthe frequency-dependent nonlinear coefficient,which is defined as

where n2is the nonlinear refractive index,and neff(ω)is the frequency-dependent refractive index.It should be noted that this definition of nonlinear coefficient is different from the conventional definition of nonlinear coefficient that is defined as
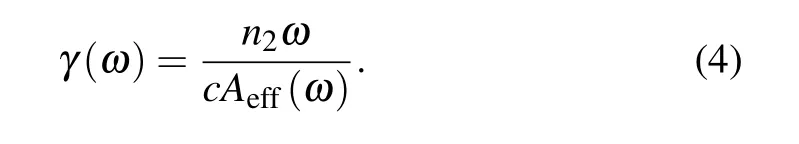
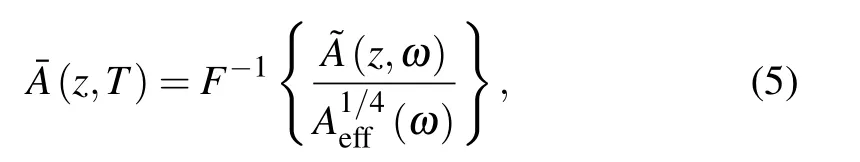
where Aeff(ω)denotes the frequency-dependent effective area,which is given by

where F(x,y,ω)is the transverse mode distribution in the fiber and R(t)is the nonlinear response function which can be obtained from
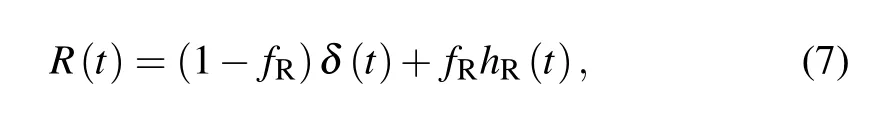
where fRdenotes the Raman contribution to the total nonlinear response and hR(t)represents the delayed Raman response and is expressed as a damped oscillation function,which is given by

Using

to change into interaction picture,the stiff dispersive part of the equation can be removed.[21]This version of GNLSE can be solved by standard Runge–Kutta method.
Shot noise of the input pulses is added based on the one photon per mode(OPPM)model,[22]which is defined as

where Tmaxis the time window of the simulation,h the Planck constant,ν the frequency,and ϕ(ν)the random phase described by the white noise which is uniformly distributed in the interval of[0,2π].The OPPM noise model is added in the frequency domain,then the field with random noise is transformed into the time domain to denote the input pulse.
The coherence can be described by the modulus of the complex degree of first-order coherence,[6]which is defined as

where the angular brackets denote an ensemble average of a great number of independently generated pairs of SC spectraand t is the time measured on the scale of the temporal resolution of the spectrometer used to resolve these spectra.The degree of coherencelies in the interval[0,1],with a value of 1 denoting perfect coherence.
3.Design of all-normal dispersion chalcogenide PCF
The conventional hexagon PCF structure is adopted to obtain all-normal dispersion properties.The cross-section of the proposed chalcogenide PCF is shown in Fig.1,where d is the air hole diameter and Λ is the pitch between two air holes.The PCF has a core made of As2Se3surrounded by five rings of circular air holes where the innermost ring is filled with As2S5glass.The As2Se3glass and the As2S5glass each have a high transmissivity in the region of 1µm–17µm and 1µm–15µm,[11]respectively.All these holes have identical diameters.Such a microstructured fiber can be fabricated by rod-intube technique.[23]
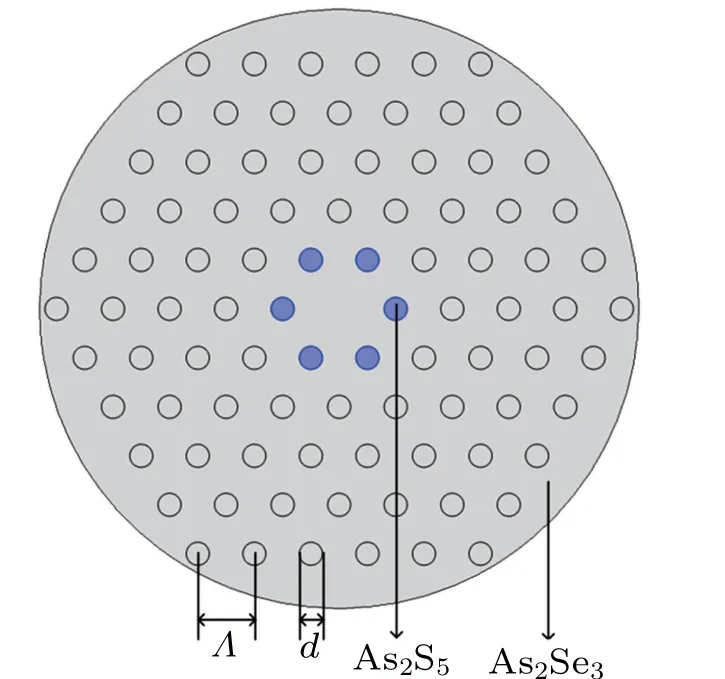
Fig.1.Cross-section of the proposed As2Se3–As2S5 PCF.
3.1.Dispersion properties of PCF
The wavelength-dependent refractive index of the chalcogenide glass is calculated from the Sellmeier equation
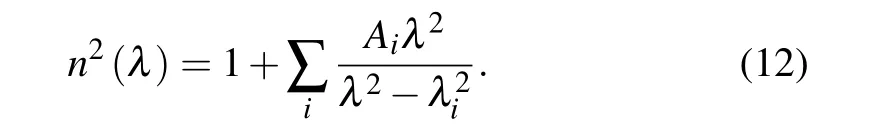
Here,the coefficients Aiand λiof As2Se3and As2S5are cited from Refs.[24]and[23],respectively.The group velocity dispersion(GVD)of the fiber is calculated from
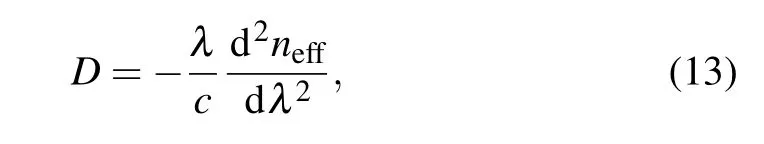
where neffis the effective refractive index calculated by COMSOL based on the full-vector finite element method.
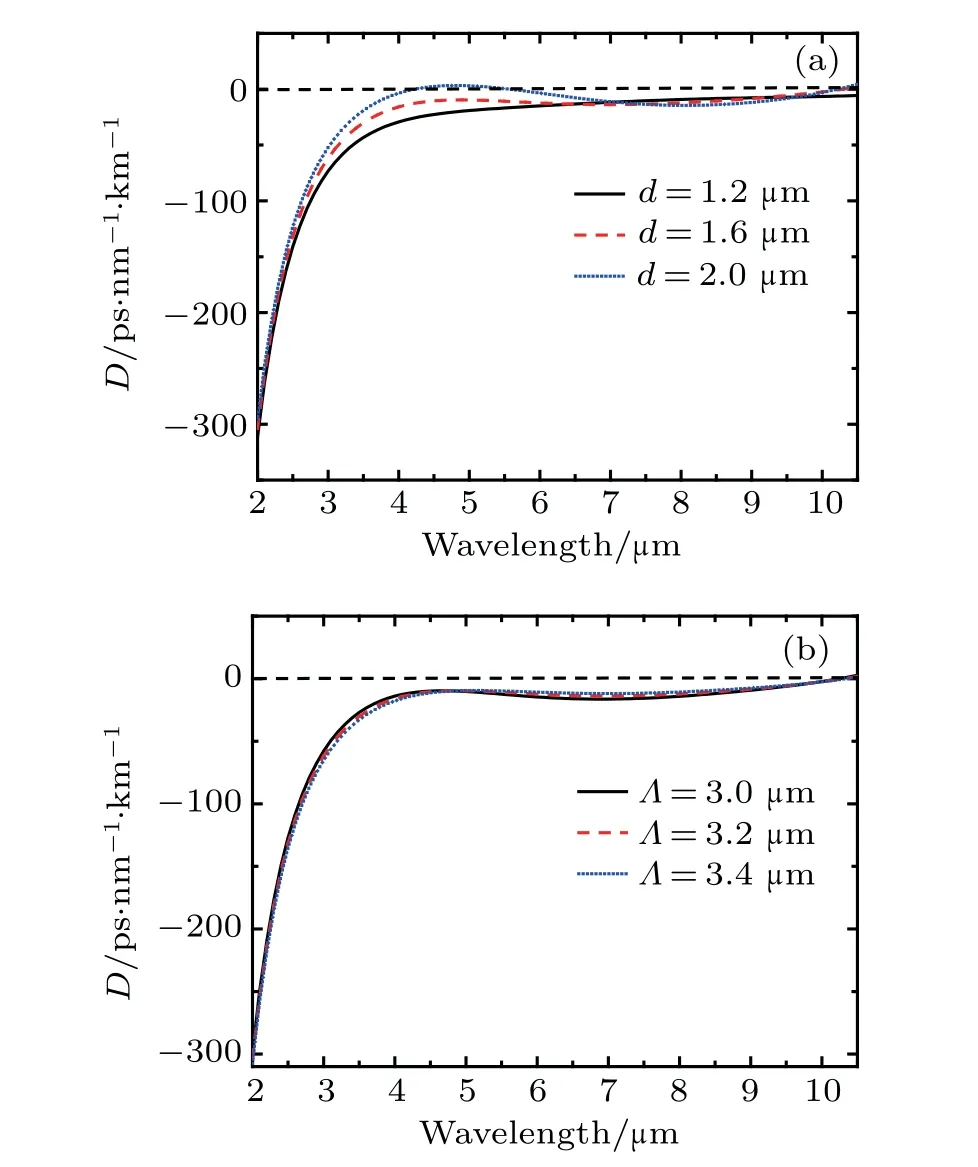
Fig.2.Plots of D versus wavelength(a)for three different d values and(b)for three different Λ values,respectively.
To obtain all-normal dispersion property of the proposed PCF,we optimized the dispersion by changing the structure parameters of the fiber. Dispersion curves of the PCF can be changed by varying the values of air hole diameter d,and the pitch Λ.Figure 2 shows the dispersion curves of the proposed PCF in a wavelength range between 2µm and 10µm.The dispersion curves with fixed Λ value at 3.2µm and varying d value are shown in Fig.2(a). As can be observed in Fig.2(a),when the air hole diameter increases,the dispersion curve moves up.When d value is smaller than 2µm,the whole dispersion curves are below the zero axis.When d value increases to 2µm,the peak of the dispersion curve enters into the anomalous dispersion region,which is related to soliton dynamics that can cause the SC coherence to degrade. The dispersion curve with d value at 1.6µm has the near zero flatted all-normal property in a 4µm–10µm region.To investigate the effect of Λ value on the dispersion characteristics,we calculated the dispersion by changing Λ value.The dispersion curves with fixed d value at 1.6µm and varying Λ value are shown in Fig.2(b).When Λ value changes,dispersion curves are nearly unchanged.For varying Λ value at 3.0µm,3.2µm,and 3.4µm,all three dispersion curves are in the normal dispersion region.According to the dispersion curves mentioned above,we chose the chalcogenide PCF with d value at 1.6µm and Λ value at 3.2µm as the optimized all-normal dispersion fiber.The corresponding dispersion curve is shown in the red dashed line in Fig.2(a).
3.2.Effective mode area and nonlinear coefficient of PCF
The effective mode area and the nonlinear coefficient are calculated by Eq.(6)and Eq.(4),respectively,which are shown in Fig.3.The value of n2is 2.3×10−17m2/W.[1]The black line and the red line indicate the effective mode area and the nonlinear coefficient,respectively.As can be observed in Fig.3,the efficient mode area increases with wavelength increasing,while the nonlinear coefficient has an opposite trend.The effective area and the nonlinear coefficient at 3µm are 15µm2and 3.22 W−1·m−1,respectively.
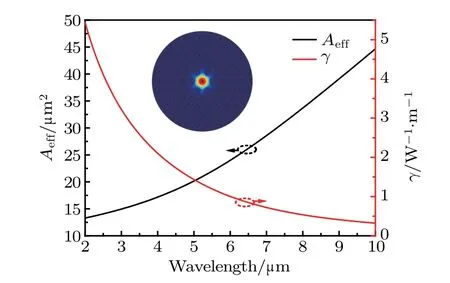
Fig.3. Calculated effective mode area and nonlinear coefficient versus wavelength of proposed all-normal dispersion PCF(Λ=3.2µm,and d=1.6µm),with inset showing fundamental mode distribution at 3µm of proposed PCF.
4.Results and discussion
According to the obtained all-normal dispersion curve,first,we numerically study the chalcogenide PCF pumped with hyperbolic secant pulses at 3µm,which can be obtained in an Er3+-doped ZBLAN fiber laser.[25]The fundamental mode distribution at 3µm of the proposed PCF is shown in the inset in Fig.3,which indicates that the optical field is confined in the PCF core. The GVD at 3µm has a value of −61.7 ps·nm−1·km−1.For As2Se3-based fiber,fR=0.148,τ1=23 fs,and τ2=164.5 fs are considered in the simulation.[26]In order to investigate the effect of pulse parameters(peak power and pulse width)on the obtained SC,we solve the GNLSE by MATLAB with a series of varying pulse parameters.
We first pump 3-cm PCF with 100-fs pulses. The obtained spectra at the output of the PCF pumped with 4 kW–16 kW are shown in Fig.4.The obtained spectrum width increases with peak power increasing.As the pump peak power increases,the short wavelength edges of the generated SCs decrease little while the long wavelength edges increase obviously.When the peak power reaches 16 kW,the generated SC covers the wavelength region from 1.4µm to 9.9µm at a−40-dB level.The long wavelength edge is nearly 10µm.
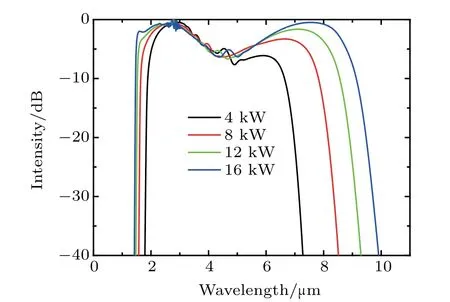
Fig.4.Simulated output spectra in 3-cm PCF(Λ=3.2µm,d=1.6µm)when pumped at 3µm with 4-kW–16-kW pulses(pulse width:100 fs).
When the peak power increases to 16.8 kW,the output SC rises from 1.4µm to 10µm.The corresponding spectral and temporal evolution along the 3-cm chalcogenide PCF are shown in Figs.5(a)and 5(b),respectively.At the first stage of the SC generation,self-phase modulation is dominated.This causes the spectrum to broaden symmetrically.After several millimeters’propagation,the spectrum broadening is dominated by optical wave breaking.Because the pulse propagates in the normal dispersion region,longer wavelength components travel faster than shorter wavelength components,which causes different wavelengths to overlap in the time domain.[27]This phenomenon results in the generation of new frequencies on both sides of the spectrum.The onset position of OWB can be calculated from
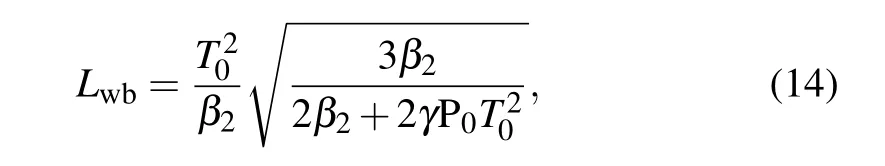
where T0is the pulse width,β2is the group velocity dispersion,and P0is the peak power of the pulse.[15,27]The calculated onset distance of OWB is 0.5 mm.It means that the OWB occurs at the very short distance,which can be observed from Fig.5(a).The corresponding spectral and temporal output are depicted in Figs.5(c)and 5(d),respectively.
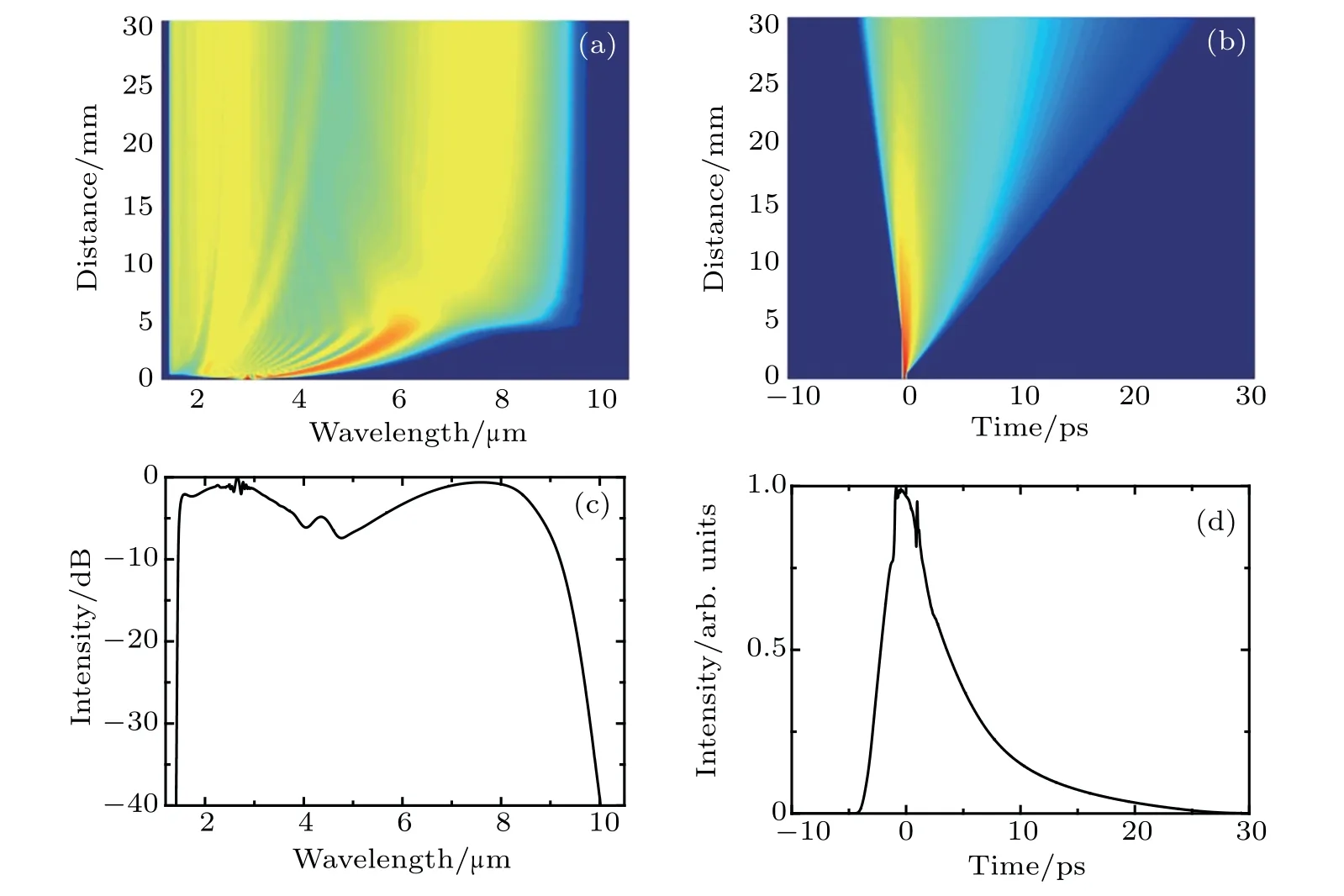
Fig.5.(a)Simulated spectral and(b)temporal evolutions along the fiber,(c)simulated spectral output,and(d)simulated temporal output,obtained on condition that 3-cm chalcogenide PCF is pumped at 3µm with 100-fs pulses with 16.8-kW peak power.
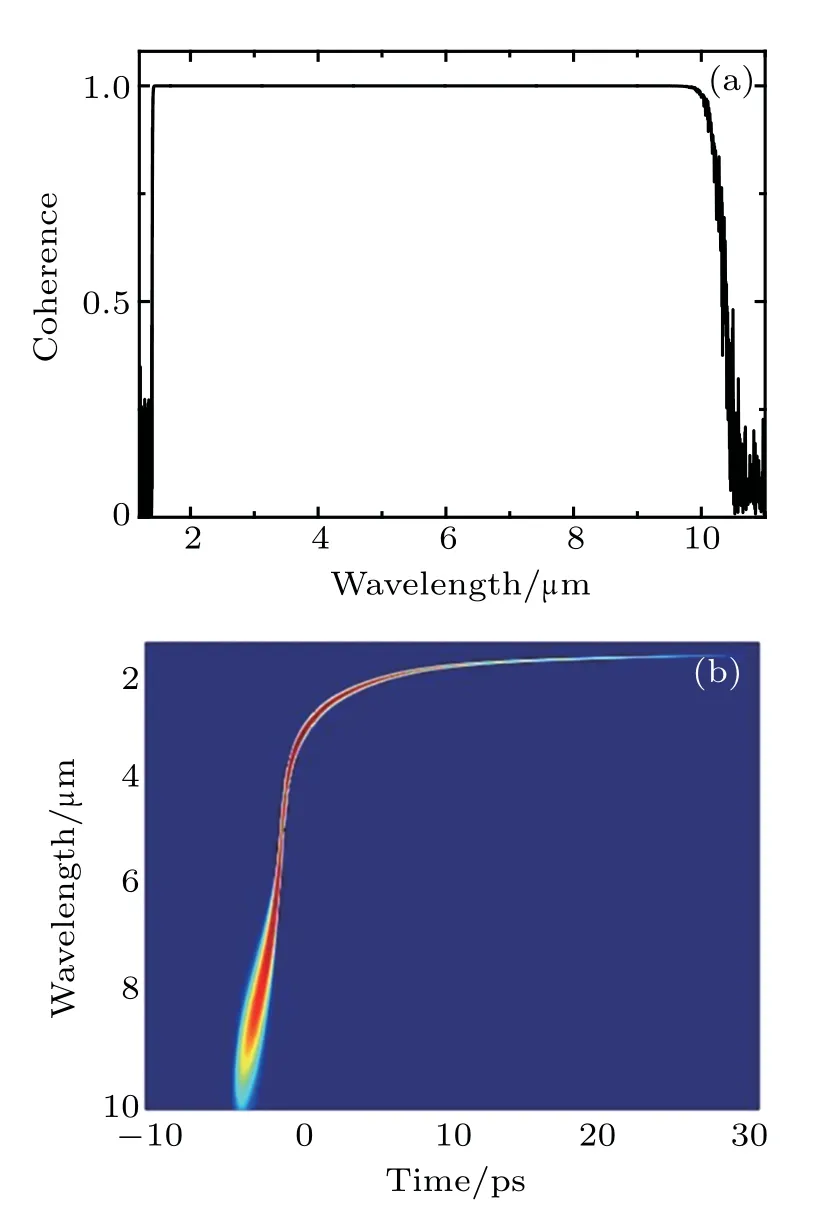
Fig.6.(a)Simulated modulus of complex degree of first-order coherence and(b)spectrogram of the output SC,with 3-cm chalcogenide PCF pumped at 3µm by 100-fs pulse with 16.8-kW peak power.
To investigate the coherence characteristics of the generated SC,we conduct 20 independent simulations with random noise described by OPPM model,which generates 190 pairs of SC spectra.The calculated modulus of complex degree of first-order coherence of the output SC is shown in Fig.6(a).As can be seen from the figure,the degree of coherence has a value of 1 in the entire spectrum,which indicates perfect coherence.The spectrogram can reveal spectral and temporal characteristics of pulses simultaneously. The corresponding spectrogram is depicted in Fig.6(b). It shows that the obtained SC has no separated components in both time domain and frequency domain,which further confirms the coherent characteristics.

Fig.7.Simulated spectra and coherence of the generated SCs,with 3-cm chalcogenide PCF pumped at 3µm by pulses with peak power of 16.8 kW and pulse duration of(a)100 fs,(b)200 fs,and(c)300 fs,respectively.
To investigate the influence of pulse width on the SC,we carry out simulations by changing pulse widths.Figure 7 shows the spectra and coherence of the generated SCs when pumped at 3µm with 100-fs–300-fs pulses.As pulse width increases,the spectrum has more oscillation components,and the spectrum width decreases. Compared with longer pulse duration,shorter pulse duration undergoes stronge SPM effect,which causes a wider SC spectrum at the same distance.When pump pulse duration increases,the generated SC is still highly coherent.By using ultra-short pulses,broadband and highly coherent SC can be obtained.
The pump wavelengths of the simulations mentioned above are 3µm. At this pump wavelength,the dispersion of the PCF is −61.7 ps·nm−1·km−1. A smaller value of dispersion is beneficial to the low pump power. The optimized dispersion curve has near-zero flatted characteristics in a region of 4µm–10µm,which provides the wide selection of pump wavelengths.The peak of the dispersion curve in the 2µm–8µm region is at 5µm with a value of only−9.6 ps·nm−1·km−1.According to this small GVD,we pump 3-cm PCF with 100-fs pulses at 5µm. At this pump wavelength,a peak power of 2.7 kW can generate an SC covering 2.7µm–10µm at a −30-dB level.The corresponding spectral evolution and the output SC are shown in Figs.8(a)and 8(b),respectively.The spectrum broadening is also dominated by SPM and OWB.The spectrogram and the coherence of the obtained SC are depicted in Figs.8(c)and 8(d),respectively,indicating the perfect coherence in the entire spectrum.

Fig.8. (a)Simulated spectral evolution,(b)simulated spectral output,(c)simulated spectrogram,and(d)modulus of complex degree of first-order coherence of the output SC,with 3-cm chalcogenide PCF pumped at 5µm with 100-fs pulses and 2.7-kW peak power.
5.Conclusions
In this paper,we proposed a novel As2Se3–As2S5PCF.When Λ=3.2µm and d=1.6µm,the optimized near-zero flattened all-normal dispersion curve is obtained.Such dispersion characteristics provide a wide selection of pump wavelengths.The highly coherent SC covering 1.4µm–10µm is achieved when pumped at 3µm. The generated SC covers 3-µm–5-µm and 8-µm–10-µm atmospheric windows. Furthermore,we investigate the influence of pulse parameters on the output SC.By using ultra-short pulses,the broadband and highly coherent SC spectrum can be generated. The simulation results provide a potential all-fiber realization of the broadband coherent MIR-SC.
杂志排行
Chinese Physics B的其它文章
- Compact finite difference schemes for the backward fractional Feynman–Kac equation with fractional substantial derivative*
- Exact solutions of a(2+1)-dimensional extended shallow water wave equation∗
- Lump-type solutions of a generalized Kadomtsev–Petviashvili equation in(3+1)-dimensions∗
- Time evolution of angular momentum coherent state derived by virtue of entangled state representation and a new binomial theorem∗
- Boundary states for entanglement robustness under dephasing and bit flip channels*
- Manipulating transition of a two-component Bose–Einstein condensate with a weak δ-shaped laser∗
