Unconventional phase transition of phase-change-memory materials for optical data storage∗

Nian-Ke Chen(陈念科) and Xian-Bin Li(李贤斌)

State Key Laboratory of Integrated Optoelectronics,College of Electronic Science and Engineering,Jilin University,Changchun 130012,China

Keywords:light–matter interaction,phase-change memory,non-thermal phase transition,optical data storage

1.Introduction

Phase-change memory(PCM)was proposed by Stanford Ovshinsky in 1968.[1]The information storage of PCM relies on the big contrast of the electronic or optical properties between the crystalline phase(with low resistance and high reflectance)and the amorphous phase(with high resistance and low reflectance)of PCM materials.The data writing and erasing operations are realized by the reversible phase transitions between the two phases.Since the operating stimuli also can be electronic or optical pulses,it can be used for both electronic and optical memory technologies.[2–5]PCM is firstly commercialized as optical memory including CD,DVD,and BD-RE.[6]These optical disks have been the main media for data storage for about 20 years.During the last two decades,the electronic devices,including computers,mobile phones,and so on,developed much faster than optical devices. Accordingly,the electronic PCM devices gradually became the main stream of PCM technology. Recently,however,the optically controlled phase-change memory restores the vitality due to the emergence of new applications,such as integrated all-optical non-volatile memory,[7]optically controlled in-memory computing,[8]and brain-inspired computing,[9,10](see Fig.1).The integration of optical memory on a chip[see Fig.1(a)]demonstrates a practicable device architecture towards new types of memory or computing devices that beyond traditional optical disks.The in-memory computing[see Fig.1(b)]means the recording and computing are realized in the same physical module,and thus can significantly enhance the computing efficiency and reduce the energy cost by avoiding the continual data transfer between the memory and the processor.In other words,it can break through the von Neumann bottleneck.The brain-inspired computing[see Fig.1(c)]is mainly realized by fabricating the artificial neuros/synapses which are suitable to achieve the functionality of neuromorphic computing towards artificial intelligence and deep learning.

Fig.1. The applications of phase-change memory in optical memory and in-memory/neuromorphic computing. (a)The integrated all-optical nonvolatile memory based on PCM material Ge2Sb2Te5(GST).Here,the PCM material is placed on the top of a waveguide. The data recording is realized by the optical near-field effects.The writing and erasing operations are achieved by the laser pulse passes through the waveguide while the read operation relies on the transmission signal modulated by the optical absorption of PCM materials.(b)The illustration of in-memory arithmetic computing by optically-controlled phase change.(c)The all-optical neuromorphic computing system based on PCM material GST.The input pulses can induce the phase change(recrystallization)of PCM material,which in turn changes the output signals.Both the in-memory computing and the neuromorphic computing utilize the accumulation effect of the crystallization.Panel(a)is reproduced from Ref.[7]with permission from the Nature Publishing Group.Panel(b)is reproduced from Ref.[8]with permission from the John Wiley and Sons.Panel(c)is reproduced from Ref.[9]with permission from the Nature Publishing Group.

Although the data processing at present is mainly dealt by electronic computers,the data transmission is dominated by optical communications in optical fibers.Therefore,repeated conversions between the electronic and the optical information are needed.If the data can be directly dealt by optical computing technology,the processing efficiency will be significantly enhanced.Moreover,the power consumption of optical computing also is believed to be lower than that of electronic computing.[11]As demonstrated by previous progresses,[7–9]optically controlled PCM should be a promising candidate for the advanced memory or computing technologies in the future.In addition,the laser-induced phase transition of PCM materials also shows potential in some other novel applications,such as the thermal emitter,[12]the thermal camouflage,[13]the plasmonic beam switching of metasurface and the bifocal lensing.[14]New opportunities are often companied by new challenges. Either in-memory computing or brain-inspired computing needs a fine control of the structures,properties and the phase-change dynamics of PCM materials. In this article,we review the understanding of laser-induced phase transitions in PCM materials which is the key for this technology.The dynamic process,the speed,the property change,the stability,the reversibility,and the cyclability of the transition closely influence the performances of PCM devices.Optical PCM involves both thermally and non-thermally driven phase transitions while electronic PCM mainly drives by Joule heating.Owing to the absence of violent thermal melting,the nonthermal phase transitions show some superior performances on the fine control of PCM materials by achieving unconventional phase transitions.However,the underlying mechanisms are still not fully understood due to the complicated light–matter interactions. Here,we mainly focus on the dynamic mechanism of laser-induced non-thermal phase transitions at atomic scale to provide fundamental supporting for optically controlled phase-change memory or computing.

2.Solid-to-solid amorphization induced by optical excitation

For optical PCM,the stimuli is laser pulse and the signal contrast(0/1)comes from the large difference in optical reflectance between the two phases(see Fig.2).[15,16]Traditional understanding of the effect of laser pulse is heating.[5]During the amorphization process,a strong but short laser pulse heats the material over its melting point and thereby turns the material into its liquid phase. After the laser pulse irradiation,the liquid is rapidly cooled down to freeze the disordered atomic arrangement and thus transforms into its amorphous state.This process is called the melt-quenching process.For the recrystallization process,a weak but long laser pulse heats the materials over its glass-transition temperature and then triggers the spontaneous recrystallization process. The thermally driven phase transitions under laser irradiation explains the work principle of PCM quite well before.[2,5,17–24]Thus,it has been believed to be the undoubted mechanism of PCM for several decades.

Fig.2.The traditional mechanism of the melt-quenching and the recrystallization processes.The crystalline phase possesses a high reflectance while the amorphous phase possesses a low reflectance.

However,in 2011,by first-principles calculations,Li et al. proposed that a non-thermal effect of the optical excitation played important roles in the ultrafast laser-induced amorphization in PCM materials.[25,26]When electrons are excited from valence band to conduction band,the chemical bonds are weakened due to the electron transfer from bonding states to anti-bonding states.Such an instability mechanism also has been suggested in the femtosecond(fs)laser-induced disordering of Si and GaAs.[27,28]The results of the ab initio molecular dynamics(AIMD)simulation in Figs.3(a)–3(f)demonstrates that upon an excitation with an intensity of 9%valence electrons,the prototypical phase-change materials Ge2Sb2Te5(GST)amorphizes within 24 picosecond(ps)at 700 K without thermal melting. In other words,the non-thermal effect of electronic excitation enables a solid-to-solid amorphization.This can also be confirmed by the mean square distance(MSD)during the AIMD simulations in Fig.3(g),where the atomic diffusion of the solid-to-solid transition is negligible compared with that of the normal melting. Without violent thermal diffusions,the speed and the cyclability of the phase transition should be enhanced indicating better performances of PCM.AIMD simulations with different excitation intensities and temperatures also demonstrate that the amorphization temperature is in proportion to the excitation intensity. As displayed in Fig.3(h),the higher the excitation intensity,the lower the amorphization temperature.At atomic scale,the excitation in phase-change materials shows an element-selective feature which makes Ge atom play a critical role in the phase changes.From the density of states(DOS)and the projected electron density in Figs.3(i)–3(k),it can be inferred that Ge atoms contribute more states than Sb atoms for the band-edge excitations.The excitation makes Ge atoms favor the sp3hybridization instead of the p-bonding in crystalline phase.[26]Therefore,the excitation drives Ge atoms from the original octahedral sties to the new tetrahedral sites and thus triggers the amorphization in the way like“umbrella flip”.[18]

The non-thermal amorphization is also supported by some recent experiments. For example,Konishi et al. have reported that the fs laser irradiation in Ge10Sb2Te13can result in an ultrafast(∼500 fs)decrease of the reflectivity[see Fig.4(a)].[29]With relatively low laser fluences(12.8 mJ/cm2),the decreased reflectivity can recover gradually. When the fluence reaches 18.1 mJ/cm2,a long-lived decrease of the reflectivity can be observed indicating a permanent amorphization.Moreover,the scanning electron microscopy(SEM)measurement in Fig.4(b)shows that the grain boundary contrast inherent to a polycrystalline structure remains unchanged.Therefore,they claimed that this is a nonthermal amorphization without melting.Siegel et al.also analyzed the time-resolved reflectivity of GST irradiated by fs laser[see Fig.4(c)].[30]After irradiated by a relatively high laser fluence(60 mJ/cm2),the reflectivity rapidly decreases and then slightly recovers to the value of amorphous phase.Considering the fact that the reflectivity of the liquid-phase GST is lower than that of the amorphous GST,[31]the change of the reflectivity under the 60-mJ/cm2irradiation is in consistent with the melt-quenching amorphization process.As such the reflectivity minimum should represent the value of liquid GST.In contrast,with a laser fluence of 36 mJ/cm2,the reflectivity directly turns to the amorphous value without reaching the liquid value,which implies a non-thermal amorphization without melting[see Fig.4(c)]. In addition,compared with nanosecond(ns)laser,fs laser can induce the amorphization of GST with a faster speed and a lower fluence.[30]This phenomenon can also be explained by the non-thermal effect.For an ns laser,the pulse duration is much longer than the characteristic time of energy transfer from excited electrons to phonons.Therefore,thermal melting should be the dominant process.For an fs laser,the energy of excited electrons cannot be completely transferred to lattice within the pulse duration.Then,the above-mentioned non-thermal effect should play important roles in the amorphization of PCM materials with a temperature lower than the melting point.

Fig.3.Electronic-excitation-induced solid-to-solid amorphization in GST.(a)–(f)Structural snapshots during the AIMD simulation of amorphization under a 9%excitation.The crystalline structure turns to a disordered phase within 24 picoseconds(ps).(g)Mean square distances(MSD)during the AIMD simulations of the excitation-induced amorphization and the normal melting.The blue line indicates the exited state(Exc.)while the red line represents the melting state(Mel.).(h)The change of amorphization temperatures with different excitation intensities.The data are obtained from a series of AIMD simulations with different excitation intensities and temperatures. The red line is a quadratic fitting. (i)Partial density of states of GST.Upon a laser excitation,electrons are mainly excited from valence band maximum,i.e.,the region labelled by“j”.Panels(j)and(k)show the projected electronic density distribution of the energy regions indicated by“j”and“k”in panel(i),respectively.Obviously,for the band-edge excitation,Ge atoms contribute more electronic states than Sb atoms.Panels(a)–(g)and(i)–(k)are reproduced from Ref.[26]with permission from the American Physical Society.Panel(h)is reproduced from Ref.[25]with permission from the John Wiley and Sons.

Fig.4.Femtosecond(fs)laser-induced amorphization of PCM materials.(a)Time-resolved reflectivity of Ge10Sb2Te13 after a 140-fs laser irradiation.The reflectivity intensity of PCM material decreases within 500 fs and then maintains for at least several tens of ps.(b)Scanning electron micrograph of a GST surface after irradiated by an 18.1-mJ/cm2 fs pulse.The dotted circle indicates the irradiated area where grain boundaries can be clearly seen.(c)Timeresolved reflectivity of the GST upon an fs laser irradiation.The data of different fluences are adopted from different areas of a light spot.The red dashed line indicates the reflectivity of liquid phase.(d)Time-resolved white line intensities of XANES of GST during the 600-ps laser-induced amorphization(red dots and line).Obviously,the intensities during amorphization are still far from the intensity of liquid state.Panels(a)and(b)are reprinted with permission from Ref.[29]©The Optical Society.Panel(c)is reproduced from Ref.[30]with permission from the AIP publishing.Panel(d)is reproduced from Ref.[33]with permission from the American Physical Society.

Since optical reflectivity only indicates an electronic structure,[32]Fons et al.have used the white line intensity of x-ray absorption near edge structure(XANES)to detect the amorphization process via structural information.[33]Obviously,the results in Fig.4(d)demonstrates that a subnanosecond laser makes GST change to its amorphous phase without turning into its liquid phase. The authors also attributed the phenomenon to a non-thermal mechanism.They suggested that the laser selectively excites the weaker bonds in GST which leads to the rupture of resonant bonding and thus results in the collapse of crystalline structure. Such a mechanism has also been proposed in GeTe by first-principles calculations,where a certain lattice distortion destroyed the resonant bonding and thereby spontaneously triggered a nonthermal amorphization.[34]

Recent years,time-resolved x-ray/electron diffractions have been utilized to directly catch the dynamic structural transitions.Waldecker et al.compared the time-resolved signals of dielectric function and x-ray diffraction(XRD)of GST under an fs laser irradiation[see Figs.5(a)and 5(b)].[35]While the dielectric function decreases sharply after the pump laser pulse,the XRD intensity decreases gradually indicating a time-domain separation of electronic state from structural evolutions.The authors also estimated the lattice temperature via a Debye–Waller-type analysis based on an assumption that the phonons are close to a thermal distribution at all delay times.At the threshold laser fluence for amorphization,the estimated lattice temperature is close to the melting point of GST.According to these results,they suggested that the abrupt decrease of dielectric function comes from the ultrafast destruction of resonant bonding,while the structural amorphization is a result of thermal melting.However,this issue still needs further investigation,because the assumption of thermal phonon distribution and the above-mentioned non-thermal effect seem to be controversial.Although a certain degree of thermal effect is inevitable during a laser irradiation,whether the thermal melting can be completed within 5 ps is also questionable.Mitrofanov et al.also investigated the phase change dynamics of fs laser-irradiated GST by time-resolved XRD and x-ray absorption fine structure(XAFS).[36]A decrease of diffraction intensity without thermally-induced peak shift within 4 ps has been observed with indication of a non-thermal disorder effect.They proposed that the disruption of resonant bonding triggers local atomic distortion and thus leads to a long-lived intermediate state[see Fig.5(c)].The difference of XAFS signals between the intermediate state and liquid phase excludes the thermal melting process in this study. Hada et al. also studied the 400-nm fs laser-induced phase change dynamics in GST by time-resolved electron diffraction.[37]They suggested that the optical excitation-induces non-thermal amorphization of GST by triggering the motion of Ge atoms from octahedral to tetrahedral sites which is in consistent with the theoretical analysis.[26]

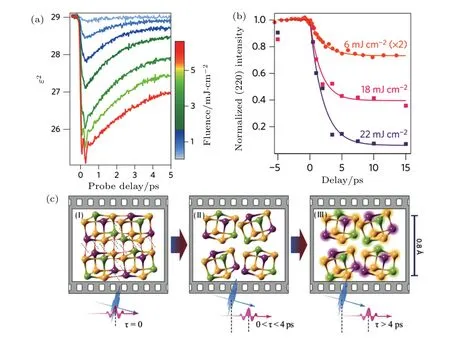
Fig.5.Time-resolved(a)imaginary part of the dielectric function and(b)XRD intensity of GST after the fs laser irradiation.The intensity of the dielectric function dramatically decreases and then recovers to a certain degree which seems to be a behavior of electrons.In contrast,the intensity of XRD decreases slowly but remains stable which is regarded as the change of structures.(c)Schematic illustrations of the excitation-induced intermediate phase by structural rotation.Panels(a)and(b)are reproduced from Ref.[35]with permission from the Nature Publishing Group.Panel(c)is reproduced from Ref.[36]with permission from the Nature Publishing Group under a Creative Commons Attribution 4.0 International License(CC BY 4.0).

3.Mechanical effects of optical excitation

In addition to the local atomic motions,the optical excitation can also lead to global volume changes. For example,by time-resolved x-ray diffraction,Fons et al.detected a large volume expansion in the fs laser-irradiated Ge2Sb2Te5.[38]Their analyses suggested that the volume expansion cannot be explained solely by a thermal expansion.The first-principles calculations also proposed a giant expansion effect of electronic excitations. The excitation-induced expansion can be explained by the quantum electronic stress effect[see Figs.6(a)and 6(b)].[39]By moving electrons from the valence band to the conduction band with atomic positions unchanged,the inner stress instantly appears due to the change of energy surfaces by the excitation.The global stress can be written as follows:[39]

Here,∆n is the excited electron density,andis the effective deformation potential induced by an excitation.In GST,when the excitation intensity is larger than 6%,the effect of the stress is to drive the volume expansion[see Fig.6(a)].According to Eq.(1),the stress by excitation should be in proportion to the effective deformation potential and excitation intensity which has been confirmed by the calculations in a series of semiconductors[see Fig.6(b)].Since diamond and BN have very large deformation potentials,their excitation stresses are extremely large.Therefore,the excitation stress should be a general effect that is adapted for other materials.

Fig.6.(a)The stresses and corresponding volume changes as a function of excitation intensity in rock-salt GST.Here,the negative stress leads to lattice expansions.(b)The stress as a function of the excitation intensity in a series of semiconductors.The inset shows the schematic illustration of inter-band excitation.CB and VB mean the conduction band and valence band,respectively.(c)The projected forces on individual atoms under a 15%excitation in rock-salt GST.The length of arrows indicates the magnitudes.(d)The magnitude of forces on Te atoms with different neighboring vacancies and excitation intensities in rock-salt GST.All panels are reproduced from Ref.[39]by permission of the PCCP Owner Societies.

To understand the rule of local atomic motions upon excitation,forces on individual atoms were studied by firstprinciples calculations in crystalline GST.[39]The local forces in rock-salt GST under the excitation display random directions[see Fig.6(c)]. As such,fs-laser pulses usually make crystalline GST disordering. The underlying reason should be closely related to the unique structure for rock-salt GST,which have randomly distributed cations(Ge/Sb/vacancy)in the sub-lattices.For the magnitude of the atomic force on Te,it not only increases with the excitation intensity but also increases with the number of neighboring cation vacancies[see Fig.6(d)].In brief,both the direction and magnitude of the excitation force on an individual atom can be adjusted by the local symmetry of a material. If a particular structure can be designed,such as a superlattice GST,the excitation forces may be controlled with desired directions. These rules of atomic forces under optical excitation may offer some routes to control phase transitions to lower the power consumptions of PCM.[19,40]

4.Order-to-order phase transition induced by optical excitation

Although non-thermal phase transition has been demonstrated in some cases,the final result is usually an amorphization that is similar to the case by the thermal meltquenching process. Surprisingly,in the most recent reports,Hu et al.and Matsubara et al.have observed an fs laserinduced rhombohedral-to-cubic phase change in GeTe by time-resolved electron diffraction and XRD,respectively[see Figs.7(a)–7(c)].[41,42]Such an order-to-order phase transition not only is helpful to understand the rule of initial atomic motions upon excitation but also shows the ability of laser controlling phase change in atomic scale that beyond the conventional amorphization. However,the mechanism of this phenomenon still has intensive debates.Hu et al.suggested that the phase transition is realized by direct motions of Te atoms along[001]axis[see Fig.7(c)]and a subsequent shear deformation.[41]Matsubara et al.proposed that the cubic signal is an average effect of Ge-atoms rattling around the center positions under the excitation[see Fig.7(d)].[42]Meanwhile,a previous theoretical calculation has suggested that the long and short bonds in GeTe will be randomly distributed by the excitations[see Fig.7(e)].[43]This average effect of the random distribution could result in a cubic-like symmetry or a pseudo cubic phase. Therefore,the observed signal of rhombohedral-to-cubic transition has received quite different explanations.

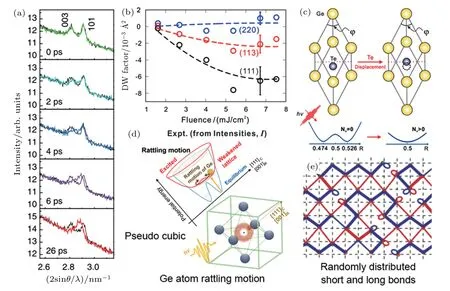
Fig.7.(a)Time-resolved XRD spectra of GeTe after fs-laser irradiations.The black lines are the XRD spectra before excitation for comparing.The merging of(003)and(101)peaks indicate the symmetry transition from rhombohedral to cubic.(b)The Debye–Waller factor deduced from the intensity of electron diffraction as a function of laser fluence.By comparing with theoretical simulations,the change of intensities is also demonstrated to be an indication of the symmetry transition from rhombohedral to cubic.(c)The schematic illustration of Te-atom displacement model where the cubic symmetry is a direct result of Te-atom movement.(d)The schematic illustration of Ge-atom rattling model where the Ge atoms dynamically move around the center of cubic sites.The average effect leads to a signal of cubic symmetry.(e)The schematic illustration of randomly distributed long and short bonds.The diffraction signal of such a structure also shows a cubic symmetry.Panels(a)and(d)are reproduced from Ref.[42]with permission from the American Physical Society.Panels(b)and(c)are reproduced from Ref.[41]with permission from the American Chemical Society.Panel(e)is reproduced from Ref.[43]with permission from the American Chemical Society.

To clarify the debates, Chen et al.performed firstprinciples calculations and real-time time-dependent density functional theory molecular dynamics(TDDFT-MD)simulations for GeTe by optical excitation.[44]TDDFT-MD is an advanced method to properly describe the excited-state behaviors because it contains the non-adiabatic electron–electron and electron–phonon couplings that beyond the traditional molecular dynamics simulations based on Born–Oppenheimer approximation.[45,46]The simulation with a 5%excitation intensity successfully reproduces the experimentally observed rhombohedral-to-cubic phase transition(Fig.8). Due to the Peierls distortion,rhombohedral GeTe possesses a distortion along[001]axis that leads to three long bonds and three short bonds around a Ge or Te atom.When electrons are excited from valence band to conduction band,the electrons are mainly transferred from Te atom to Ge atoms[see Fig.8(a)].Then,the potential energy surface can be changed from a double-well shape to a single-well shape[see Fig.8(b)].As such,the increased gradient of potential energy instantly produces forces on Ge and Te atoms along the[001]axis or the z direction[see Fig.8(d)]. Driven by the directional force,Ge and Te atoms coherently move to the opposite directions along[001]axis which activates the A1gphonon modes.As a result,the long bonds and short bonds flip back and forth as shown in Fig.8(e). Upon damping of the A1gmode,the long and short bond lengths gradually transform to an equivalent value indicating a phase transition from rhombohedral to cubic phase.This is a truly rhombohedral-to-cubic transition rather than a pseudo one due to some sort of averaging effect.The temperature throughout the simulation is lower than the Curie temperature(700 K)of GeTe and thereby excludes the thermally induced phase transition[see Fig.8(f)].The atomic trajectory in Fig.8(c)reveals that,the transition relies on collective motions without the traditional nucleation-and-growth process or atomic diffusion. Therefore,the phase-transition speed can be as fast as 1 ps.

Moreover,the kinetic energy and momentum of Ge and Te atoms that projected in three dimensions(x,y,z)show a strikingly higher component along[001]axis or z direction due to the excitation[see Figs.8(g)and 8(h)]. This phenomenon clearly demonstrates the process is not the random thermal motion,which should have similar situations for the three different directions.In fact,the nominal temperature in Fig.8(f)is a result of atomic motions including all the directions.Here,the authors recalculated the true thermal temperature just including atomic motions along x and y directions,which is not affected by the excitation[see the blue line in Fig.8(f)].The thermal temperature during the phase transition is clearly lower than 500 K.Therefore,the excitation-induced rhombohedral-to-cubic phase transition in GeTe is indeed a non-thermal process.Such a kind of order-to-order transition induced by fs laser not only represents a new type of phase transition but also supplies opportunities for exploring ultrafast phase change memory or some new optoelectronic applications.

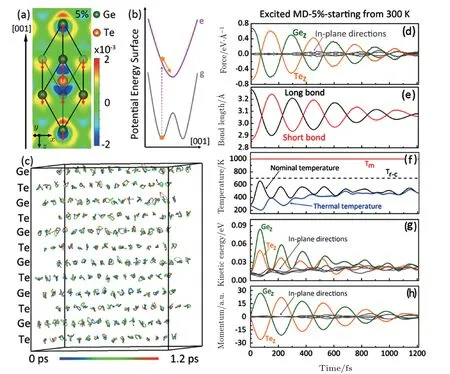
Fig.8.(a)The electron density distribution upon the 5%excitation in rhombohedral GeTe.The red arrows indicate the force acting on atoms.(b)The change of potential energy surface of GeTe due to electronic excitation.(c)The trajectories of atomic motions during the TDDFT-MD simulation of the phase transition in GeTe with a 5%excitation.Time evolution of(d)average force,(e)bond length,(f)temperature,(g)kinetic energy,and(h)momentum during the TDDFT-MD in GeTe under a 5%excitation.All panels are reproduced from Ref.[44]with permission from the American Physical Society.

5.Conclusion and perspectives

In this work,some recent progress on ultrafast laserinduced unconventional phase transitions in phase-changememory materials are summarized to the community.Traditional understanding on the laser-induced amorphization is a thermally driven melt-quenching process.As the laser pulse duration becomes very short(e.g.,femtosecond scale),the non-thermal effect of electronic excitation would play significant roles in the phase changes.First-principles calculations reveal the solid-to-solid amorphization in GST under optically electronic excitation. Analysis on electronic structures suggests that electronic excitation drives Ge atoms to move from the octahedral to the tetrahedral sites and thus triggers the amorphization very fast. Non-thermal amorphization of GST without melting is also supported by a series of experiments.Time-resolved reflectivity obtained by the pump-probe technology shows an amorphization process of GST without experiencing a liquid phase.Time-resolved XRD also shows locally structural changes of GST without melting,including local distortions and volume expansions. Furthermore,two recent experiments with time-resolved XRD and electron diffraction techniques both observed an order-to-order(rhombohedral-to-cubic)phase transition in GeTe by fs laser which is in contrast to the usual amorphization of PCM materials induced by laser.Due to the absence of atomic pictures in real time and real space,the underlying mechanism has been intensely debated.By TDDFT-MD,the atomic driving force and phase change dynamics are revealed.Owing to the change of potential energy surface upon electronic excitation,directional forces along[001]axis are instantly produced which directly drives the phase transition.The molecular dynamics simulations suggest that the order-to-order phase transition in GeTe can happen within 1 ps because it is completed by coherent atomic motions without the nucleation-and-growth process and the atomic diffusions.These unconventional phase transitions in PCM materials show the ability of ultrafast laser to manipulate structure beyond thermal melting.Compared with the conventional amorphization via a melt-quenching process,the solid-to-solid amorphization involves much less atomic diffusions.Moreover,the order-to-order phase transition not only possesses a speed with about 3 orders of magnitude faster than conventional phase-change random access memory,but also can control the property of phase-change materials with minimal atomic movements.Therefore,these unconventional phase transitions could be a promising route to promote optical storage and future optical computing with faster speed,lower power consumption,and better endurance.

Acknowledgments

We thank Prof.Shengbai Zhang at Rensselaer Polytechnic Institute and Prof. Hong-Bo Sun at Tsinghua University for their supports on the topics of this work.The High-Performance Computing Center(HPCC)at Jilin University for calculation resources is acknowledged.On the occasion of the 100th birthday of Prof. Kun Huang,we sincerely acknowledge him for his great efforts and long-term contributions on the semiconductor science in China.