Opto-electromechanically induced transparency in a hybrid opto-electromechanical system∗

Hui Liu(刘慧), Li-Guo Qin(秦立国), Li-Jun Tian(田立君),‡, and Hong-Yang Ma(马鸿洋)

1Department of Physics,Shanghai University,Shanghai 200444,China

2School of Mathematics,Physics and Statistics,Shanghai University of Engineering Science,Shanghai 201620,China

3Shanghai Advanced Research Institute,Chinese Academy of Sciences,Shanghai 201210,China

4School of Science,Qingdao University of Technology,Qingdao 266000,China

Keywords:opto-electromechanical system, opto-electromechanically induced transparency, pump–probe spectroscopy

1.Introduction

Over the past two decades cavity quantum electrodynamics(QED)has the blooming developments and become one of the most promising setups to investigate the interactions between light and matter at the quantum level.[1,2]The progress has shown that cavity QED offers an interesting tool to implement quantum manipulation technology. For example,cavity-induced transparency[3]is an electromagnetically induced transparency(EIT)-like effect.[4]The EIT-like effect provided large valuable contributions and important roles in a variety of quantum processes,such as nonlinear susceptibility modulation,[5]light switch,[6]quantum memory,[7]and quantum communication.[8]

As a novel extension of the cavity,cavity opto-mechanics system is usually composed of Fabry–Pérot(FP)cavity with one fixed mirror replaced by a mechanical oscillator as a movable mirror,where the optical field in the cavity can couple to the mechanical oscillator via the radiation pressure.[9]Recently such cavity opto-mechanics has become one of the most promising platform to study the interactions between optical and mechanical modes or between optical fields and atoms,and has attracted increasing interest in both theory and experiment.[9,10]More importantly,some theories in QED can be further extended to the cavity optomechanics,[10]where many interesting phenomena and effects have been theoretically predicted then experimentally demonstrated, such as opto-mechanically induced transparency(OMIT,EIT-like),[11–13]frequency transfer,[14]and normalmode splitting.[15]In addition,this system can be applied to studying the cooling of mechanical oscillator,[16,17]precision measurement,[18–21]quantum information transfer,[22,23]etc.When the combination of opto-mechanical system with atoms or the nitrogen–vacancy centers in various hybrid systems allows for light switch,[24]electro-optic waveform interconnect,[25]the strong coupling of the mechanical oscillations to the atomic spin[26]and phonon-induced spin–spin interactions.[27]Therefore cavity opto-mechanics system has shown significant advantages and may be applicable to future quantum networks.[10]

The transmission spectroscopy of the cavity is of crucial importance to control the propagation and absorption of optical field in practical application. Therefore,the output of cavity opto-mechanics is widely studied,especially the OMIT effect caused by the destructive interference.[28]However,the OMIT with a single transparency window in the frequency domain limits the manifold functionalities for nonlinear optics and optical communication.[10]In recent studies,the single-OMIT has been extended to the double transparency windows in the divers opto-mechanical modes.The double transparency can be induced by two charged nano-mechanical resonators with Coulomb interaction,[29]the coherent oscillations of the two mechanical oscillators,[30]two tunneling-coupled resonators,[31]two coupling opto-mechanical cavities,[32]and coupling the mechanical resonator to a two-level system.[33]Further,multiple-OMIT was also found in multiple-cavity opto-mechanical system coupled to one two-level atom.[34]It is worth noting that the multiple-OMIT in the nanostructure system can be applied in all-optical communication,[31]all optical quantum network,and multi-channel quantum information processing.[35]Therefore it is very valuable and significant to research the manipulation of the multiple-OMIT.

In order to break frequency limitation of the transparency window and realize multiple-channel optical communication,[10]this device should satisfy the following conditions:(i)the multiple transparent windows;(ii)controllable transparent windows;(iii)advantageous integrability on the chip.For this purpose we propose a scheme to manipulate the opto-electromechanically induced transparency(OEMIT)with multi-windows in a hybrid opto-electromechanical device consisted of two tunneling coupled cavities including one FP cavity and one opto-mechanical cavity.The charged mechanical mirror of the opto-mechanical cavity is capacitively coupled to another charged mechanical oscillator by the Coulomb interaction,i.e.,a mechanically tunable capacitor.By combining the coherent cavity,[31]opto-mechanical,[11]and Coulomb couplings[29]into a micro-fabricated hybrid opto-electromechanical module,we successively show the single,double,and triple transparency windows,i.e.,a controllable multiple-OMIT,whose width can be adjusted by changing the parameters of the system.Here the transparency is a hybrid opto-electromechanically induced transparency.This integrated device including functions of three of induced transparency will excite a development trend and implementation prospect towards the integration quantum module device.

The paper is organized as follows.In Section 2,we introduce the hybrid opto-electromechanical model and theoretical equations.We will discuss OEMIT in our system and propose a scheme to modulate the transparency windows of OEMIT in Section 3.Finally we give the conclusion.

2.Model and theory

The hybrid opto-electromechanical system(HOEMS)under consideration is shown schematically in Fig.1.The system consists of an FP cavitytunneling-connected to a cavity opto-electromechanical system,which includes a typical optomehcanical cavityand a variable capacitor.As an interface,the nanomechanical oscillator(NMO)not only couples to the cavity fieldby the radiation pressure but also capacitively interacts with another mechanical oscillatorby the Coulomb interaction.The FP cavity is separately driven by a strong pump field εcwith frequency ωcand a weak probe field εpwith frequency ωp.In the rotating frame,the total Hamiltonian of the HOEMS can be written as

where

Fig.1.The schematic diagram of the HOEMS.The FP cavity is tunneling coupled to an opto-mechanical cavity ,where the charged NMO as a mechanical mirror of the opto-mechanical cavity is capacitively coupled to another charged NMO by the Coulomb interaction.J is the tunneling coupling strength between the two cavities.The HOEMS is driven by a strong pump field εc and a weak probe field εp.The output field at the probe frequency of the HOEMS is εout.

Considering the effects of noise terms on the cavity fields and NMOs,the Langevin equations of the HOEMS are given by the following expressions[37]

where γm1,m2describe the damping rates of the mechanical modes1,2,respectively.is the input noise operator with zero mean value.The quantum Brownian noisewith zero mean value comes from the coupling between the NMOand its own environment. Therefore,the noise terms are negligible in the case of the mean response.Under the condition of mean field approximation with operator factorizationwhereandare two arbitrary operators,[11]the dynamic equations of the system can be written as

In order to simplify these nonlinear equations,we can take a semi-classical approach by consideringwhich allows us to write down each operator as a linear sum of the steadystate mean value and a small quantum fluctuation,i.e.,

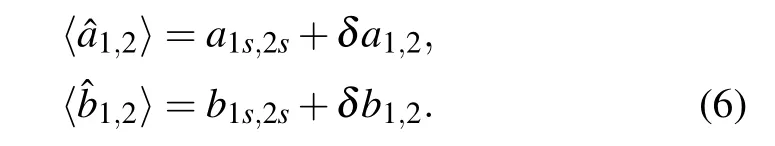
Here the steady-state value of the operator comes from the influence of the strong pump light and the weak probe light causes the quantum fluctuation. After inserting Eq.(6)into Eq.(5),and neglecting the second-order terms,we can obtain the steady-state mean values of the system as

where G=ga2sis the effective opto-mechanical coupling strength between the optical modeand the mechanical modeFor simplicity,we consider two identical NMOs with m1=m2=m,ωm1=ωm2=ωm,and γm1=γm2=γm,but it is not essential. In addition,we assume that the HOEMS is operating under the conditions of the resolved red sidebandand,the NMOs withand[31]Based on the rotating-wave approximation,with the rotation transformand δb1,2=−i∆t,the steady-state equations of quantum fluctuation can be derived as

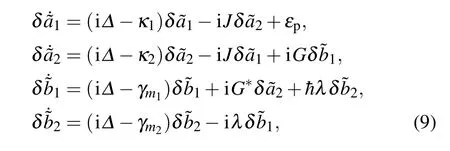
where ∆=δ −ωmis the effective detuning of the probe field from the cavity resonance frequency.Under steady-state condition,the solution of the first intracavity fieldcan be given by

In order to find the response of the system to the probe frequency, by the output field based on the input–output theory,[11,31]we can obtain

For the opto-electromechanically induced modification of the probe field in the HOEMS,we define the term εTas

The real and imaginary parts of εTdescribe the absorption and dispersion of the HOEMS,respectively.[11]

3.Opto-electromechanically induced transparency with tunable multi-transparency windows in output field

Now we present the opto-electromechanically induced multi-transparency in the HOEMS and study the manipulation of OEMIT in the different cases.We find that the number and width of the OEMIT windows can be modulated and some interesting phenomena can be observed. Here we employ the parameters from the recent experiment,[12,31]where the mass m=20 ng,the frequency ωm=2π×51.8 MHz,the damping rate γm=2π×41 kHz,and the wavelength of the cavity field λc=1064 nm,and the power the pump laser Pc=80 mW and the single photon coupling strength g=2π×2.16 kHz.

If the tunneling-coupling strength between two cavity fields J=0,i.e.,the system only includes an FP cavity driven by the pump and probe fields,figure 2(a)shows the usual absorption and dispersion of the optical field with no transparency window. The output field becomes εT=2κ1/(κ1−i∆),which only depends the first cavity decay κ1and the detuning ∆.

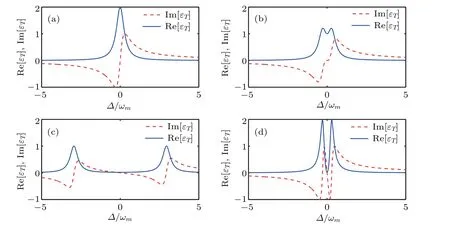
Fig.2.The absorption Re[εT](blue-solid line)and dispersion Im[εT](red-dotted line)as a function of the detuning ∆with no opto-mechanical coupling g=0 in the different cases(a)κ1=κ2=2π×15 MHz,J=0;(b)κ1=κ2=2π×15 MHz,J=κ1;(c)κ1=κ2=2π×15 MHz,J=10κ1;(d)κ1=100κ2=2π×15 MHz,J=κ1.

When the opto-mechanical coupling g is negligible within Eq.(10),the output field can be rewritten as

which has the standard form of the single coupled-cavityinduced transparency.[38]As the coupling strength J gradually increases,the absorption peak of the probe field in Fig.2(a)begins to split into two peaks,i.e.,a dip appears and finally reaches a state with no absorption.From Figs.2(b)and 2(c),we can find that the transparency window can be widened and the dip can be deepened by the strong coupling J when the other parameters are not changed. If the decay of the second cavitydecreases,i.e.,the quality of the coupling cavity becomes high,the dip can be also deepened,as shown in Figs.2(b)and 2(d).These show that the single-transparency window is induced by the strong coupling cavity field.

Fig.3.The absorption Re[εT](blue-solid line)and dispersion Im[εT](red-dotted line)as a function of the detuning ∆in the case of and the other parameters are the same as those in Fig.2(c).

Further considered the opto-mechanical coupling and ignoring the Coulomb coupling,the output field can be given by

Then the behavior of the probe output field become the standard form of the double-EIT,[31]which is caused by the coupled opto-mechanical-induced transparency.[31,32]Its real and imaginary parts are shown in Fig.3.A new absorption peak appears inside the transparency window in Fig.2(c)due to the effect of the opto-mechanical coupling.The double OMIT is presented due to quantum interference effects.The explanation of OEMIT can been given by the energy level configuration in Fig.4. With the coupling of two cavities,the normal optical mode splits into two modes and the EIT-like window of the output field is established based on the destructive interference[38]as shown in Eq.(14).When the NMO1is coupled to the second cavity via the opto-mechanical interaction,which is involved in the interference process,therefore the opto-mechanical interaction destroy the single EIT and splits one transparency window into two,i.e.,two dips appear as shown in Fig.3.The central peak is narrower than the both sides because of

Fig.4.Energy level structure of the HOEMS.The number states of photons and phonons are denoted by Ni and ni,respectively. The tunneling coupling strength betweenandis J,and the effective opto-mechanical coupling strength betweenandis G. The Coulomb coupling strength betweenandis λ.

Fig.5.The absorption Re[εT]as a function of the detuning ∆and λ is plotted in panel(a)and the corresponding two-dimensional elevation diagram is given in panel(b),when the Coulomb interaction is added into the system.The other parameters are the same as those in Fig.3.

4.Conclusion

In summary,we proposed a scheme to implement the manipulation of the opto-electromechanically induced transparency based on OMIT in a hybrid opto-electromechanical device composed of an FP cavity tunneling-coupled to a hybrid opto-electromechanical system. By studying the probe output field of the FP cavity,we found the OEMIT with the tunable multi-transparency windows.When the tunneling coupling is considered and the opto-mechanical coupling is negligible(g=0)with the high quality opto-mechanical cavity,we can find a single coupled cavity-induced transparency,where the strong J and weak κ2can enhance the width of the transparency window. Further,the Coulomb coupling is not added into the system considering the case of g0 and J0,the output field gives the double OMIT with the single window split into two transparency windows due to the opto-mechanical coupling. Finally,the tunneling,optomechanical and Coulomb couplings are considered,the triple-OMIT appears with electromechanical induced an additional transparency window due to a degenerate level induced a new interference channel,where the width of transparency window can been widen by increasing λ.Therefore,by studying the effects of the different coupling parameters on the output field,we gave a scheme to modulate the number of transparency windows and its width.We believe that our results would be helpful for further understanding and applying quantum interference effects,especially,in the aspect of the integration quantum module device.