Structural and electronic properties of transition-metal chalcogenides Mo5S4 nanowires∗

Ming-Shuai Qiu(邱明帅),Huai-Hong Guo(郭怀红),†,Ye Zhang(张也),Bao-Juan Dong(董宝娟), Sajjad Ali(阿里.萨贾德), and Teng Yang(杨腾),‡

1College of Sciences,Liaoning Shihua University,Fushun 113001,China

2Shenyang National Laboratory for Materials Science,Institute of Metal Research,Chinese Academy of Sciences,Shenyang 110016,China

Keywords:transition-metal chalcogenide nanowire

1.Introduction

One-dimensional materials, such as nanotubes and nanowires,have been attracting considerable attention for decades for the significance on exploring fundamental physics at low dimensions and also as building blocks for materials in nanoscale electronic and mechanical device applications.[1–5]Carbon nanotubes(CNTs)in particular as almost perfect 1D systems have been studied intensively in multidisciplinary research and for multifunctional applications. However the drawback of CNTs has remained for long,such as difficulty in chirality-controlled synthesis,catalysis contamination,non-Ohmic electrode contact,and difficulty to separate bundled tubes.[6]Combining subnanometer size with structural stability,uniform electronic properties,and many advantages over CNTs,transition-metal chalcogenide nanowires(TMCN)have been studied widely as a potentially viable alternative to CNTs for many applications.[7–9]

So far,a plethora of TMCN structures have been synthesized in experiments. All the possible forms of atomic structures can be summarized in Fig.1.The basic and rigid structural unit is the M6octahedron of transition metal atom M,which is decorated by chalcogenide X atoms.Depending on how M6octahedra condensate into the extended structure,as we understand,three types of one-dimensional M backbones can be categorized as presented in Figs.1(a)–1(c).(i)The first type,with lateral edges of M6octahedra shared,is a chain of trans-edge sharing M6,as shown in Fig.1(a). This type of extended structure usually takes the form of M4X6as defined as M4X6edge in Fig.1(a),and is mostly observed in the reduced molybdenum oxides[10,11]in which the M6units are edge-bridged by oxygen atoms,such as M6X12on the left side of the lower panel in Fig.1(a). (ii)The second type is the face sharing of M6condensing into an extended Chevrel phase,[12]as indicated in Fig.1(b). This process is often observed when the M6clusters are face-bridged by the chalcogenide ligands such as S,Se,and Te.[8,13–15]The extended structure is derived from the basic unit of M6X8with chalcogenide atoms decorating the eight faces of the M6octahedra,as defined by M6X6cap in Fig.1(b).Besides the Chevrel-phase M6X6cap structure,a hybrid structure(M6X8cap+edge in Fig.1(b))has also been reported with mixed cap and edge decoration positions of chalcogenide.[7,16]The M6octahedron in this structure,which is face-decorated by chalcogenide ligands X,is edge-bridged by three chalcogenide ligands to the neighboring M6octahedron.Such an M–X–M bridge exhibits very interesting bistable and stress-tunable electronic properties.[7,17](iii)The two types of structures shown above can be derived from the trans-edge sharing(two M atoms sharing)and face-to-face(three M atoms sharing)of two neighboring M6octahedra,it is reasonable to wonder if an extended structure can be as well constructed based on vertex-tovertex(one M atom sharing).In this manner,the third type is shown in Fig.1(c),which takes possible forms of chalcogenide face-bridged(M5X4cap)or edge-bridged(M5X4edge)structures,both of which have a ratio of X/M as low as 4/5.The third type has been found to be stable in M5X4cap type structures such as Ti5Se4,[18]Ti5Te4,[19]Nb5Se4,Nb5Te4,[20]and W5As2.5P1.5.[21]The M5X4edge structure was rarely seen but recently obtained from the top-down synthesis by electron beam etching on 2-dimensional MoS2.[22]

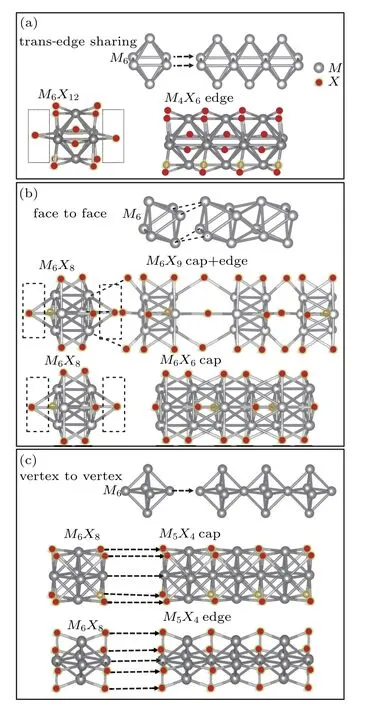
Fig.1.Categorization of plethora of transition metal chalcogenide nanowires MxXy constructed from the M6 octahedral building block. (a)Trans-edge sharing to form M4X6 nanowires. (b)Face-to-face to form M6X9 or M6X6 nanowires.(c)Vertex-to-vertex to form M5X4 nanowires with the least X/M ratio so far.The upper structures in panels(a)–(c)are to show how possible nanowire geometry forms from M6 building block,and the lower structures are to show the exemplary extended nanowires which have mostly been synthesized in experiment.M and X atoms are shown in silver grey and brown,respectively.

The nanowires arising from the vertex sharing of M6attracted our most attention,not only due to the success in synthesis with a low X/M ratio which might be environmentally friendly,but also because of the smallest cross-section area among all TMCN nanowires available.[7,23–26]The crosssection size of nanowires is intimately related to quantum confinement,a more pronounced confinement effect than its sibling ribbon or wire structures is therefore anticipated and may give rise to much enhanced electronic properties than its bulk counterpart.[27–29]However,its structural stability and electronic properties are still unclear.How is it compared to the other TMCN nanowires reported?What are exactly their electronic structure?Is is possible to obtain a more stable geometry by making full use of the construction rules proposed here?

To address these problems,we select Mo and S elements and study the structural stability and electronic properties of vertex-sharing Mo5S4nanowires and compare them with similar nanostructures in terms of convex hull of binding energy and phonon dispersion relation. We confirm that the experimentally obtained edge structure is stable from the binding strength and phonon dispersion relation.Interestingly,a new structure(the so-called C&E)with mixed cap and edge units is predicted here and appears more stable than the cap or edge structures. The calculated energy barriers of Peierls phase transitions from cap and edge to C&E are 0.9 eV and 0.3 eV per unit cell,respectively,suggesting that it is likely to achieve by a structural phase transition. Crystal orbital overlapping population(COOP)is also calculated to study the bonding character.COOP shows that the cap structure is unstable due to the partial occupation of anti-bonding states,while both the edge and C&E structures are stable from the COOP analysis.All three Mo5S4phases are semiconductors with indirect band gap.Note that a band nesting appears in the band gap region of the C&E structure,and can be well fit for the optoelectronic sensor in the infrared spectrum.

2.Method

To study the structural stability and potential applications of transition metal chalcogenides nanowires,we carried out density functional calculation with the projector augmented wave method[30]as implemented in the Vienna ab initio simulation package(VASP).[31]The exchange correlation potential was approximated by generalized gradient approximation(GGA)proposed by Perdew,Burke,and Ernzerhof.[32]To describe well-isolated nanowires while using periodic boundary conditions,we used a tetragonal lattice with a large interwire separation of 20.We sampled a 21×1×1k mesh in the Brillouine zone. A 400 eV energy cutoff of the plane wave basis was used. The total energy precision was better then 0.1 meV/atom.The Hellman–Feynmann theorem and CG algorithm were used to obtain equilibrium structures.The convergence was set as 10−6eV in energy and 0.01 eV/˚A in force.

On the basis of the equilibrium structures,the phonon dispersion relation of nanowires was calculated based on density functional perturbation theory[33]as implemented in the PHONOPY code.[34]A 3×1×1 supercell size and 10×1×1 q mesh were used.

Crystal orbital overlapping population[35,36]was used to evaluate all pairwise interactions between two orbitals(ithand jth)of two atoms(at R and)by the product of overlap matrix and density of states matrix elements

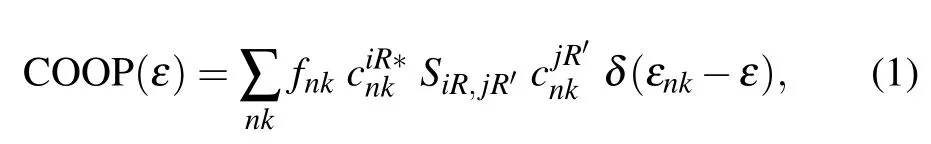
where n is the band index,k is the reciprocal wave vector,fnkis the Fermi–Dirac distribution function,and εnkis the energy band. The system wave functionwith the ithatomic orbital φiRat the R site.is the overlap matrix. Positive,zero,and negative values of COOP represent bonding,non-bonding,and anti-bonding states,respectively.[35,36]

3.Structure

To form a stable extended nanowire structure,Mo6octahedral unit and how sulfur decorates the rigid unit are both essential.In regard to how sulfur decorates,the two most stable cluster structures,Mo6S12and Mo6S8,can give us a good hint.As shown in Fig.2(a),both clusters have the Mo6octahedra.Sulfur finds a niche either by decorating the eight Mo3triangle faces to form Mo6S8,or by bridging the twelve Mo–Mo bonds to form Mo6S12.Likewise,when forming into an extended nanowire,the residing way of sulfur atoms should play as important a role as the condensation of Mo6units.

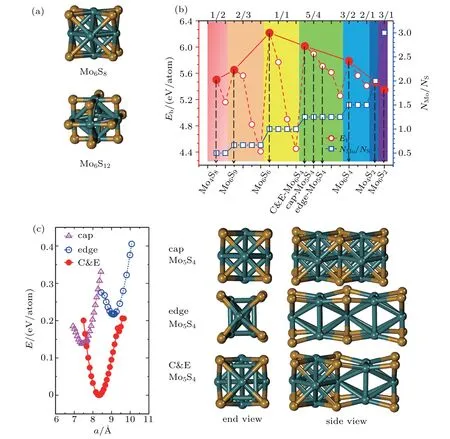
Fig.2.(a)Two primary cluster structures Mo6S8 and Mo6S12 with face-bridged and edge-bridged chalcogenides,respectively.(b)Binding energy as a function of stoichiometry and structure of MoxSy nanowires.Stoichiometry ratio x/y is grouped into different color zones,the most stable structures are represented in filled red dots,while the rest in empty red dots.Square blue is to show the value of x/y,or NMo/NS.(c)Energy–lattice constant curve and atomic structures of Mo5S4 nanowires of cap,edge and C&E.The edge structure has been reported experimentally.[22]Both cap and C&E types are derived based on the construction strategy in Fig.1.

Guided by the strategy,we constructed possible atomic structures at different stoichiometries,i.e.,Mo:S=1:2,2:3,1:1,...,and each stoichiometry has several candidate structures.The binding energies for the optimized structures are shown as filled and empty red dots in Fig.2(b). The binding energy is defined as Eb=[E(MoxSy)−xE(Mo)−yE(S)]/(x+y),in which E(MoxSy),E(Mo),and E(S)refer to the total energies of MoxSynanowire,Mo atom,and S atom,respectively. It is not surprising to see that among the optimized structures(geometries given in Fig.A1),the most stable ones,as given by filled red dots in Fig.2(b),have the similar structural characters,namely,the rigid Mo6unit with sulfur decorating either the triangle face or bridging the Mo–Mo bond.Encouragingly,from our calculations,the most stable atomic structures predicted for Mo:S=2:3 and 1:1 are Mo6S9and Mo6S6nanowires,respectively.Such a result substantiates the face to face strategy to construct a nanowire in Fig.1(b),and is also well supported by the previous studies.[7,8,17]Moreover,for the stoichiometry Mo:S=3:2 and 2:1,we obtained the most stable structures of Mo6S4and Mo4S2nanowire,which are actually decided by the transedge sharing strategy(Fig.1(a)).As the ratio of Mo over S goes 3/1 or higher,Mo6rigid unit seems not observable in the final structures,probably because too few sulfur atoms in the structure are not sufficient to decorate the Mo atoms and Mo6unit therefore is much deformed.

More interesting is the stoichiometry Mo:S=5:4 given in the green zone in Fig.2(b).The three most stable structures from our calculation are referred to the C&E,cap,and edge Mo5S4.Besides the edge structure,which has been achieved from the top-down synthesis,[22]we have found here two new structures,the cap and C&E ones,both of which are more stable than the edge structure.From the energy–lattice constant curve and the optimized atomic structures given in Fig.2(c),one can first see a larger lattice constant of the edge than that of the cap,while the C&E has its lattice constant lying between the two of them due to the mixed units from both the cap and edge.The relevance between the three structures can be seen more clearly from the end view in Fig.2(c).The simplest structure is the cap,with an unit cell of 5 Mo plus 4 sulfur atoms.To get the edge from the cap structure,the crosssection square of Mo6octahedra first rotates by 45◦,the unit cell doubles,and then the two central Mo atoms are shifted slightly away from the center in opposite directions normal to the nanowire axis.To get the C&E from the cap is easier,doubling the unit cell size of the cap,followed by rotating one of the Mo4square by 45◦.

We already see from the binding energy that two new structures(cap and C&E)are more stable than the experimentally observed edge Mo5S4nanowires.But it is still not clear whether they are stable dynamically.We are also curious whether it is plausible to obtain the new and stable structures from the one available. Moreover,the electronic properties,which have not been studied yet,need to be calculated before any potential applications can be conceived.

4.Stability

To check the dynamic stability and possible route for synthesis,we performed phonon dispersion relation and nudged elastic band(NEB)calculation.From the phonon dispersion relation shown in Fig.3(a),the edge and C&E phases do not have any negative values of eigenfrequency,indicating that both phases are dynamically stable and can be synthesized in lab. While the cap phase has a negative eigenfrequency close to the zone edge area,suggesting a tendency of structural phase transition,for example,a Peierls transition by doubling the unit size.

Fig.3. (a)Phonon dispersion relation for the three types of Mo5S4 nanowires.Reaction coordinates for structural change(b)between the edge and the C&E structures,(c)between the cap and the C&E structures of Mo5S5 nanowires. The main structural change is due to the rotation of Mo-square as schematized in inset of(b)and(c).

Indeed,as mentioned in Fig.2(c),a Peierls phase transition may happen here by doubling the unit cell size along with a structural distortion.We confirm here by our NEB results that such a phase transition occurs by unit rotation.As schematized in the inset of Figs.3(b)and 3(c),the Peierls transition from either the cap or the edge nanowire to the C&E nanowire takes a form of one Mo4square rotation.The energy barrier for such a transition is about 0.3 eV and 0.9 eV per formula unit(18 atoms in total)from the available edge phase and the cap phase to the most stable C&E phase,respectively.The low barrier,together with strong binding and high dynamic stability,renders a big opportunity to achieve C&E phase from many possible means including bottom-up,top-down methods or phase transition triggered by external perturbations.

5.Electronic properties

To have an insight into the electronic properties of Mo5S4nanowires,we calculated the electronic band structure and show it in Fig.4. The cap,edge,and C&E structures are given in panels(a),(b),and(c),respectively. All the three phases have a similar band character,semiconducting and indirect band gap.The band gaps are within the infrared spectral range,about 0.12 eV(cap),0.22 eV(edg),0.27 eV(C&E),which are underestimated by the DFT calculations and should be improved by HSE or GW calculations,which is beyond the scope of this study.

Fig.4.Band structure,density of states(DOS),and crystal COOP of(a)cap,(b)edge,and(c)C&E Mo5S4 nanowires.Positive value of COOP represents bonding states and negative anti-bonding states.

When looking into both the electronic density of states(DOS)in Fig.4(b)and the COOP in Fig.4(c),one can see quickly the spikes of DOS and COOP occurring at the same energy level,especially the red solid lines in COOP,which arise from the bonding states between neighboring Mo-4d orbitals.Compared to the green dashed line due to Mo–S bonding in COOP,the backbone of Mo octahedra plays an obviously essential role in determining the band structure. It is very interesting to make a compare of COOP between the different phases in Figs.4(a)–4(c).In Fig.4(a),the anti-bonding state due to both Mo–Mo(red)and Mo–S(green)is filled in the cap structure,indicating the electronic instability of such a structure.Depopulation of the anti-bonding state,for example by hole doping[37]or liquid ion gating,[38,39]will stabilize the structure.This explains why the cap structures of Ti5Te4and Nb5Te4[18–20]are stable,simply because Ti[3d24s2]and Nb[4d45s1]both have less valence electrons than Mo[4d55s1]atoms,resembling a hole doping effect.From the cap to the edge structure,sulfur changes the way of decoration and Mo backbone expands,the anti-bonding state disappears in the edge structure in Fig.4(b).In Fig.4(c),coexist of both cap and edge decorations of sulfur shifts the anti-bonding state due to Mo–Mo above the Fermi level,stabilizing the C&E structure.

It is worth noting that,different from the zone-folding feature of bands in Figs.4(a)and 4(b),a novel band nesting(parallel bands or large joint density of states)feature shows up in the C&E band structure in Fig.4(c).One expects that if an infrared light is incident with energy matching the direct band gap at Γ point,light-induced electronic vertical excitation will happen in the whole Brillouin zone.More importantly,electron and hole will move in opposite directions,leading to optimal charge separation for optoelectronic devices,for example,an optical sensor working in the infrared spectral range.

6.Conclusion

In summary,we present a theoretical investigation on the stability and electronic properties of new types of transition metal chalcogenides Mo5S4nanowires. The stability of the predicted new structural phases(cap,edge,and C&E)are explored by the binding energy,phonon dispersion relation,and crystal orbital overlapping population analysis. The experimentally obtained edge structure is confirmed to be thermodynamically and dynamically stable.Moreover,a new and stable C&E structure having mixed cap and edge units and more stable than the edge structure is found dynamically stable.COOP analysis also substantiates the structural stability of both edge and C&E phases based on the maximally optimized bonding states.The calculated energy barrier of Peierls phase transition from the edge to C&E is about 0.9 eV per unit cell,indicating a likability to achieve the C&E phase from the experimentally available phase. All the Mo5S4phases are semiconducting with indirect band gap.Band nesting appearing in band gap region of the C&E structure makes it well fit for optoelectronic sensor applications in the infrared spectrum.

Appendix A: Atomic structures for MoxSy nanowires

Fig.A1. The atomic structures for MoxSy nanowires mentioned in Fig.2(b).The most stable structures for fixed stoichiometries are highlighted in red boxes.