基于fbprophet框架的期末余额预测方法

1.中国科学院计算机网络信息中心,北京 100190

2.中国科学院大学,北京 100049

引言

通常事业单位、私营企业的会计账户结构分为两个基本部分，一部分反映增加，另一部分反映减少。其中，登记的本期增加金额，称为本期增加发生额；登记的本期减少金额，称为本期减少发生额[1]。期末余额(Closing balance or Ending balance)是指期初余额(Opening balance or Beginning balance)加本期增加发生额和本期减少发生额相抵后的差额(亦称余额)，即在一定时期内期末(单位：可选日、周、月、季度、年等时间单位)结出的账户余额，具体公式如下：

期末余额，是随时间周期动态变化的序列数据，即属于时间序列的范畴。本文第1章详细地介绍了时间序列的概念、定义以及分别就分类和回归两个大类介绍时间序列分析(Time-Series Analysis)的有关方法。时间序列分析和预测是机器学习(Machine Learning,ML)算法、深度学习(Deep Learning,DL)算法中常见的一种类型，经常使用指数平滑法(Exponential Smoothing,ES)[3]和ARIMA 模型以及其它算法来解决时间序列中的各种问题，例如：商品销售预测[4]。

近年来，相较于传统的基于规则的模型和算法，机器学习算法和深度学习算法在股票预测、价格预测等[5,6]金融领域的时间序列分析问题中已经取得了较为显著的应用成果。但在本文研究的单位或企业每日期末余额预测问题上，目前虽有分析师或工程师选择使用 ARIMA 模型、Holt-Winters 模型进行处理，但普通的分析师们较难掌握相应的专业知识进行优化，外加数据本身情况复杂、规律性差，故而预测结果容易出现偏差。我们根据以上原因，选择FaceBook 公司开源时间序列预测框架 fbprophet。fbprophet 在当前已有的众多机器学习模型和框架中表现十分突出，一经发布，迅速成为时下时间序列分析爱好者们的首选框架之一，特别是在处理带有季节性、节假日效应的时间序列数据时，大放异彩。本文在第2 章是介绍 fbprophet的原理、结构，及选择 fbprophet的具体原因。

第3 章实验部分，首先介绍实验开始前数据的预处理，具体的步骤包括异常值和离群点处理、缺失值处理、归一化处理等操作，以及如何通过模型的可解释参数优化预测结果；其次，介绍实验的开展过程和结果对比、分析，除本文推荐的fbprophet 模型外，我们选择使用常见的多层感知器(Multi-Layer Perception,MLP)以及极端梯度提升(eXtreme Gradient Boosting,XGBoost)等模型作为对比，并分析了当前存在的不足。第4 章是最终章，展望了未来的应用领域和扩展趋势，进行总结。

本文的贡献在于，通过 fbprophet 对期末余额数据进行分析，在证明 fbprophet 对复杂多变的时间序列仍有较高准确率的前提下，为单位或企业提供了未来期末余额的预测结果，方便财务人员直接观测余额的趋势变化从而进行财务管理和资金调整。同时，通过真实数据的有效实验，证明 fbprophet 在中国科学院“新一代 ARP 系统“(简称 NEW ARP)上使用的可行性，为NEW ARP的后续功能扩展(包括财务报表分析、预测等)提供可靠意见。

1 时间序列

1.1 时间序列的定义

时间序列(Time Series)，通常是指以一定的时间间隔，按照时间先后顺序收集某种现象或某一个统计指标的数据而形成的序列[7]。其主要目的是根据已有的历史数据对其在未来某一时间段内的改变进行预测。通常，一个时间序列数据往往由以下四部分构成：长期趋势(T)、季节变动(S)、循环变动(C)和不规则变动(I)[8]。任何随时间变化而改变的变量均可以使用时间序列分析方法进行处理。

1.2 常见的时间序列分析方法

1.2.1 时间序列分类算法

通常情况下，无论是在科学研究或工程应用中，我们可获取的时间序列数据主要以回归预测问题为展开。例如：产品销售预测、价格预测、股票预测等。但随着机器学习技术和深度学习技术的不断更新以及当代数据规模呈指数倍增长的发展趋势，各式各样的想法和算法也随之产生。例如：预测某一行业内某家企业产品销售利润的变动趋势，我们并不固化地预测具体的销售利润值，而是根据选定的阈值，预测其在未来某一阶段内的波动趋势是逐步上涨还是整体下跌，而该问题属于分类问题的范畴，即时间序列分类(Time Series Classification,TSC)。目前，专注于时间序列分类问题的爱好者们通常喜欢选择多层感知器，或者全卷积神经网络(Fully Convolutional Neural Network,FCNs)以及残差网络(Residual Networks,ResNets)[9]等多种算法模型。同时，有效的解决时间序列分类问题有助于其在像心电图(ECG/EEG)信号分类等独具意义的重大领域做出贡献[10]。

1.2.2 时间序列回归预测算法

整体而言，常见的时间序列分析仍以预测未来某一个时间节点或几个时间节点的状态实际值即时间序列回归预测(Time Series Regression Prediction)问题而居多。常见的分析方法通常建立在统计学的基础之上，例如：差分整合移动平均自回归模型，又称为整合移动平均自回归模型(Auto regressive Integrated Moving Average Model,ARIMA)及其组合扩展[11]。或者可采用长短期记忆网络(Long Short Term Memory,LSTM)[12]等模型以及根据具体的应用场景进行扩展。

1.3 时间序列预测面临的问题

目前，常见的预测方法需要满足诸多假设，例如：数据的分布应满足高斯分布(Gaussian distribution)或其它分布；或满足一些平稳性假设以及一定的约束条件等。但这通常会导致算法在实际应用场景中受到严格的限制。

本文提出的问题，期末余额预测，以未来一个月(即 31天)之内单位或企业每日的期末余额为预测目标。其数据随时间动态变化，即满足时间的依赖性。

同时，现实世界背景下获取的数据往往包含大量的不确定性。在期末余额预测问题中，可能存在大量因季节性、节假日效应和业务变化等原因造成的离群点或异常值。(注释：此处的离群点和异常值并非指因记录人员登记错误、记录缺失等主观原因造成的数据异常。)

所以，在模型的选择和构造时，需要考虑时间序列数据本身是否包含趋势、周期、季节性、噪音、随机性、曲线和水平等诸多特点。若选择使用常见的机器学习、深度学习时间序列分析方法，例如：ARIMA 或 LSTM 模型，对于对时间序列领域或当前业务领域不熟悉、缺少经验的使用者们来说，较难进行有效的超参数调整、修改神经网络内部结构、添加额外的影响因素等优化工作，进而难以得出可靠的预测结果。故，本文选择使用 fbprophet 模型。fbprophet模型的原理和优点以及选择使用的具体原因如第2章节所述。

2 Facebook Prophet 介绍

2.1 fbprophet 原理和流程结构说明

2.1.1 fbprophet 原理说明

fbprophet 是 Facebook 于2017年2月24日开源的一款时间序列预测框架。托管在GitHub 上。该模型基于一个灵活的贝叶斯模型(Bayesian model)，其本质是一个可分解的时间序列模型[13]，其中包含以下三个主要的模型组建:

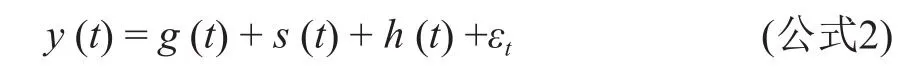
其中，g(t)是趋势函数，它就时间序列数据的非周期性变化进行建模；s(t)表示周期变化(例如：每周或每年的季节性，可根据实际业务应用场景改变时间粒度)；h(t)表示假期的影响；εt表示误差项[14]。

同时，该框架内置了直观的参数，使用者可以在完全不了解模型底层实现细节的前提下根据数据本身进行调整。正如同 Taylor SJ和Letham B 论文中所述的一样，“让对于时间序列模型和方法知之甚少的非领域人员也能够灵活地将其应用于广泛的业务时间序列中[14]。”

2.1.2 fbprophet 流程结构说明

从整体上看，fbprophet的预测流程是一个循环结构，由 Modeling、Forecast Evaluation、Surface Problems 以及 Visually Inspect Forecasts 四部分依次循环组成，反复迭代[14]。即整个过程是人工分析和自动化预测相结合的循环结构。

2.2 选择 fbprophet的理由

相较于其它时间序列预测模型和框架，fbprophet自身具备诸多优点，包括：(1)程序执行准确、快速。现如今，Facebook的许多应用程序都使用fbprophet为规划计划和目标设定提供可靠的预测结果。fbprophet 把模型放到stan中，即可以非常快速地得到预测结果[15]；(2)自动化。可自动对拟合的时间序列历史数据中的缺失值进行有效的处理[15]；(3)可对估计结果进行调整。若使用者自身具备一定程度的专业知识和业务经验，可通过调节模型自带的可解释参数，优化预测结果[15]；(4)为了方便更多的用户使用，fbprophet 提供了 Python 编程语言和R 编程语言的两类版本[15]。同时，fbprophet 框架自身内嵌可视化工具，方便使用者们直接观察预测结果。其次，同其它模型相比，整个预测流程操作简单、容易上手、使用便捷。故，我们选择 fbprophet 框架作为单位或企业日期末余额预测的预测模型。

3 实验

3.1 实验目的

本文的实验目的，是验证 fbprophet 模型相比于其它神经网络模型或机器学习算法，在操作便利的同时，面对情况复杂、变化多端、不确定性大的日期末余额时间序列预测问题时，仍可以有较好的表现，说明其具有较强的鲁棒性。方便日后向其它同类型领域或其它分支领域出现的问题进行扩展，因此，首先对数据进行了异常值和离群点处理、缺失值处理和归一化处理以及模型的参数调优；其次，我们将时间序列数据放入到fbprophet 模型和其它用于对比的机器学习和深度学习算法模型中，包括：MLP和XGBoost 等模型，通过回归预测拟合指标 -- 平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)的相关对比，观察 fbprophet 模型在真实数据上的预测结果。

3.2 数据预处理

3.2.1 数据集描述

本文使用某单位近年来日期末余额的脱敏数据。每个数据样本有两个特征，分别是“每日的日期”和“每日的期末余额”，作为fbprophet的输入。fbprophet的输入必须包含两列数据，一是时间戳，即时间信息；二是数值，代表需要预测的变量。且分别修改特征名称为“ds”和“y”(需要遵守的固定格式)。

3.2.2 异常值和离群点处理

首先，通过人工比对等方式排除数据中因工作人员记录错误等主观原因造成的异常值；其次，通过相关的业务经验设定阈值，将不满足的数据离群点剔除。

3.2.3 缺失值处理

本文使用 datatime.datatime()方法，首先核实序列中除删除的异常值和离群点外，是否存在非节假日期间数据的缺失。若存在，则使用 fbprophet 拟合历史数据时的预测值进行填充；其次，在通常情况下，单位或企业因正常的双休日、节假日休息，不会有业务往来、资本交易、现金流动等操作，即日期末余额一般不会发生变化。但为了保证时间序列的完整性，将缺失的节假日日期补充到时间序列中。并使用每周五和每个节假日(例如：五一劳动节、十一国庆节)头一天的期末余额填充相邻的双休日、节假日的缺失值。(注释：该步骤可根据业务需要酌情省略。但在其他业务场景中，例如：商场销售利润预测，具有很强的节假日效应，因为商场的销售利润通常在双休日期间会高于工作日，尤其是节假日。则需要处理缺失值并通过holidays参数添加日期。)

3.2.4 归一化处理

为了防止因输入数据过大导致模型难以便捷快速的得出预测结果，于是对数据采取归一化处理进而保证程序运行时收敛加快。归一化后的数据仍然保持原数据间的相对关系，同时一定程度上提高了数据的可比性。

可选用的数据归一化方法(Normalization Method)有：常见的min-max标准化(Min-Max Normalization)，同时也叫线性函数归一化；Z-score标准化(Z-score standardization)，也叫 0 均值标准化；以及对数归一、指数归一等多种方法。

3.2.5 参数调节

使用 fbprophet 自带的可调节参数，例如：yearly_seasonality 参数(在实例化模型时，可以为每个内置的季节性指定傅里叶级数[16])、changepoint_prior_scale 参数(默认情况下，该参数设置为0.05。增加它将使拟合趋势更加灵活[17])等，根据模型拟合时间序列历史数据后预测未来的实验结果进行调参优化，起到逐步改善模型预测精度的作用。holidays 参数同上文所述，不再重复。

3.3 实验评估指标

机器学习模型、深度学习模型需要计算评估指标，从而获取模型表现好坏的反馈，进而帮助使用者优化算法或选择模型。在回归预测问题中，常见的评估指标有：均方误差(Mean Squared error,MSE)；均方根误差(Root Mean Squared Error，RMSE)，或称为方均根偏移、均方根差、方均根差等；平均绝对百分比误差也叫平均绝对百分比偏差(Mean Absolute Percentage Deviation，MAPD)以及平均绝对误差(Mean Absolute Deviation，MAE)等。

四项评估指标各自具有不同的优缺点，本文根据实验的情况和需要选择平均绝对百分比误差作为衡量指标。其中，平均绝对百分比误差主要考虑了预测误差与数据真实值之间的比例。其范围为[0,+∞)，平均绝对百分比误差为0 % 代表模型完美，平均绝对百分比误差大于100 % 则代表模型劣质。

平均绝对百分比误差的公式如下图所示：

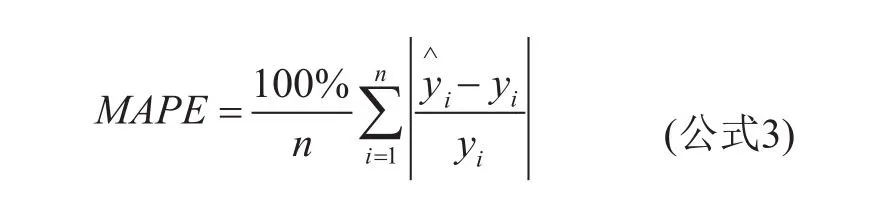
3.4 对比试验

使用 scikit-learn的MLPRegressor和xgboost 以及 MultiOutputRegressor，分别构造 MLP和XGBoost模型，同 fbprophet 模型对同一时间序列输出预测结果，并分别计算各模型预测结果和真实值之间的平均绝对百分比误差，从而进行对比。

3.5 实验过程

我们随机选择了数据集中的某一天作为划分训练集和测试集的分割点，将这一天之前的历史数据作为训练集，分别输入到MLP和XGBoost 以及 fbprophet等诸多模型中，进行拟合训练并输出预测值。通过测试集，分别得到未来 1天至31天内，各时间段的真实值和各个模型预测值之间的平均绝对百分比误差，对比 fbprophet的预测效果。

3.6 实验结论

图1 MLP、XGBoost、fbprophet 等模型预测未来一个月每日期末余额的预测结果的平均绝对百分比误差(预测天数逐步增加)Fig.1 The mean absolute percentage error of the prediction results of daily ending balance predicted by MLP,XGBoost,fbprophet for the next month(the predicted days gradually increase)

图2 fbprophet的平均绝对百分比误差趋势走向(预测天数以 7天即 1 周为单位逐步增加)Fig.2 Trend of average absolute percentage error of fbprophet(the predicted days gradually increase in unit of 7 days or 1 week)

由下文的实验图片 1的展现结果可以看出，随着各模型预测天数的增加(1天、2天、1 周最终到1个月),作为回归预测评估指标的平均绝对百分比误差期初较为动荡，中期略为平稳，后期逐步增高。经分析，期初包含的时间节点较少，1个预测值的偏差可能导致整个预测结果的误差增高。中期随着预测天数的增加使得单个偏差的影响变小，但与之同时，时间序列中包含的不确定性因素也随之增加，即中后期各模型的评估指标值也随之增加。通过观察可发现，fbprophet的增长幅度在3个模型中最为缓慢。其中，由实验图片 2 可知，fbprophet的平均绝对百分比误差值于中后期(1个月内)始终保持在0.20至0.25 上下。实验结果说明，相较于其它模型，fbprophet 在单位日期末余额预测问题等实际应用场景上具有较好的表现，达到了期望的结果。

3.7 存在的不足

在金融领域的时间序列预测问题中，相比于潜在的季节性以及节假日效应等干扰因素，存在不确定性的最大来源就在于未来趋势的不可控性。在fbprophet中，我们假设未来趋势的平均变动频率与幅度和我们观测到的历史值是一样的，从而预测趋势的变化并通过计算最终得到预测区间。但我们并没有足够的依据和手段保证该假设一定是正确的，特别是在处理规律性较差、数据分布不均匀的真实世界的业务问题。随着预测未来时间长度的不断增大，一季度、半年、一年、甚至更长的时间，伴随的不确定性有可能会呈指数倍的增长，从而导致预测结果出现较大偏差。fbprophet 除预测值 yhat 外，同时会输出一个置信区间 yhat_upper和yhat_lower，即上、下边界。我们在评估模型的预测结果时，会将 yhat的拟合结果作为主预测值，而上、下边界的预测值作为一定的参考，辅助使用者对预测结果进行判断。但随着预测天数的逐步增加，yhat_upper和yhat_lower的范围会越来越大，直至丧失准确度。

因此，如何更好的让模型在预测更长时间的未来的同时还能保持较高的准确度，即降低未来不确定性因素对模型造成的干扰，可作为今后的研究方向。

4 结语

经过实验证明，fbprophet 操作简单、容易上手。适合绝大多数对时间序列问题感兴趣的爱好者们。同时，在情况复杂多变的期末余额预测问题上，也取得了较好的预测成果,达到了我们期望的结果。可向具有同样业务需要的其它平台或系统进行推广，例如：目前中科院多个研究所都在使用的新一代 ARP系统，其中包含大量的财务分析需求，建议使用fbprophet 模型进行业务分析和预测。