最优化方法在非常规致密砂岩储层中的应用

侯振学,张国华，王文文，成家杰，王俊华，钱玉萍

(中海油田服务股份有限公司油田技术事业部，河北 廊坊 065201)

常规碎屑岩储层具有矿物简单，物性优良的特点，但是随着可开发常规油气藏资源量日益减少，勘探开发的重点逐渐转向非常规致密砂岩储层。致密砂岩气储层与常规碎屑岩相比具有岩石矿物成分复杂，孔隙度及渗透率极低的特点，必须经过大规模水力压裂才能获得较高的产能[1]，储层物性及脆性是控制储层压裂产气效果的两项重要因素[2]，而脆性则与储层中脆性矿物含量密切相关[3]。常规碎屑岩测井解释主要采用Sand程序即可对砂质、泥质含量及孔隙度进行计算，但是Sand程序主要是基于中子—密度交会图的方法对岩性及孔隙度进行简单处理，处理的结果误差较大，无法满足低孔低渗储层的精细评价需求。最优化方法为近年发展起来的一种基于体积模型及最小二乘法原理的复杂储层矿物组分及孔隙度评价方法，前人对该方法的原理进行了精细研究[4]，并分别用该方法进行了火成岩、页岩气及碳酸盐岩等复杂储层处理[5-7]，但是在致密气砂岩储层中的应用比较少见。

本文以鄂尔多斯盆地东缘上古生界石炭系本溪组—二叠系石千峰组致密砂岩储层的常规测井资料为基础，结合岩心X衍射实验分析确定致密储层的矿物组分，应用最优化方法对储层组分进行了处理，定量计算地层中的矿物组分或孔隙流体含量，进而可以计算储层孔隙度、脆性指数，计算结果与X衍射及岩心物性分析得出的矿物组分含量及孔隙度对比，吻合程度较高。根据计算的孔隙度及脆性指数可指导后期压裂及产能预测，为致密气的开发提供了重要依据。

1 方法原理

地层对于测井仪器的响应方程可由岩石体积物理模型表示。例如，声波测井的响应方程为

Δt=Δtgasxgas+Δtwaterxwater+Δtsh1xsh1+Δtsh2xsh2+…
+Δtshkxshk+Δtma1xma1+Δtma2xma2+…Δtmakxmak

(1)

式中Δtgas,Δtwater,Δtsh1,Δtsh2,Δtma1,Δtma2,…,Δtmak分别表示地层中气、水、黏土矿物(1～k种)、岩石骨架矿物(1～k种)的声波时差值，μs/m。同理，补偿中子、密度以及其它测井曲线都可以写成上述形式。公式(1)可以简写为以下形式：

(2)

其中n表示组成地层的组分个数，个；xj表示第j种组分的相对含量。同理可写出其它测井仪器的响应方程，并组成方程组，用通式表示为

(3)

式中，A表示某种组分的测井曲线响应值；m表示测井仪器的个数，个；B表示地层对测井仪器的响应值。

解以上式(3)由m个方程组成的方程组，就可以求得xj，这就是测井曲线反演地层组分。

在模型中，所求地层组分数n与测井曲线条数m组成的方程组存在以下三种情况：

①mn，方程组为超定方程，有多解，没有真解但有最优解。

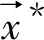
(4)

其中：c、xmaxj均为常数，在地层组分分析程序中，c=1,xmaxj为第j种组分的最大相对体积。式(4)为一带约束条件的超定线性方程组。

由最小二乘法原理，解式(4)这一带约束条件的线性方程组的问题可转换成以下求极值问题，即实际测井值与求解出的组分反算(即正演)的理论测井值残差的平方和最小：

(5)

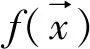
2 处理方法

2.1 区域岩石学特征

本文研究对象为鄂尔多斯盆地东缘上古生界石炭系本溪组—二叠系石千峰组地层，主要为海陆过渡相沉积[8]，岩性主要为砂砾岩、泥岩以及煤层，生储盖条件良好，但是受后期压实、胶结等复杂成岩作用影响，储层致密化[9-10]特征明显。近年来在石炭系、三叠系、二叠系发现了多套含气致密砂岩储层，预示着该地区致密砂岩气勘探具有很大的潜力。

根据石炭系本溪组—二叠系石千峰组致密砂岩储层岩心X衍射实验分析资料，致密砂岩储层矿物组分包含石英、钾长石、斜长石、方解石、白云石、黄铁矿、菱铁矿等骨架矿物以及高岭石、绿泥石、伊利石、伊蒙混层等多种黏土矿物，骨架矿物占75%左右，其中石英及斜长石含量最高，黏土矿物占25%左右，其中高岭石、伊利石及绿泥石含量最高。

2.2 建立模型

复杂的致密砂岩储层可以看成是由不均匀的几部分组成:若干种骨架矿物、黏土矿物和孔隙流体，而地层的测井值就是其中多种矿物和流体的综合响应。组成地层的组分可能有很多种，但测井曲线是有限的，因此要用有限测井信息正确反演出组成地层的全部组分是不可能的。因此，建立物理模型应遵守以下原则：①一般情况下组分的个数必须小于或等于测井曲线条数；②对地层电性有明显影响的微量矿物应加入地层组分；③地层中物理性质相近的组分可看成是同种组分；④把地层中一些含量很小的组分合并到性质与之相近的组分之中。

研究区测井曲线一般仅有自然伽马(GR)、密度(DEN)、补偿中子(CNL)、纵波时差(DTC)、横波时差(DTS)、光电吸收截面(PEF)以及深侧向电阻率(RD)、浅侧向(RS)等八条，用以求取多达十几种的储层组分显然是不可能的。根据以上原则，选择石英、长石(钾长石合并到斜长石)、方解石(白云石合并到方解石)为骨架矿物，高岭石、伊利石、绿泥石为黏土矿物，流体组分依据研究区储层生产情况选择水、气，总计八种组分建立模型。

2.3 参数确定

石英、长石、方解石等骨架矿物都有其固定的测井响应，但是黏土矿物在不同的区域会在一定的范围内变化，所以黏土矿物的响应参数需要不断地进行调整。最优化方法可以根据计算的组分含量对测井曲线进行反算(正演)，当反算的理论曲线与实测曲线差异较大的时候就需要调节相应的参数值，当二者重合的时候，说明输入的参数准确，通过不断调整黏土矿物测井响应值，使实测与理论曲线重合较好，说明此时选取的参数正确，此时各种组分的测井响应参数如表1所示。

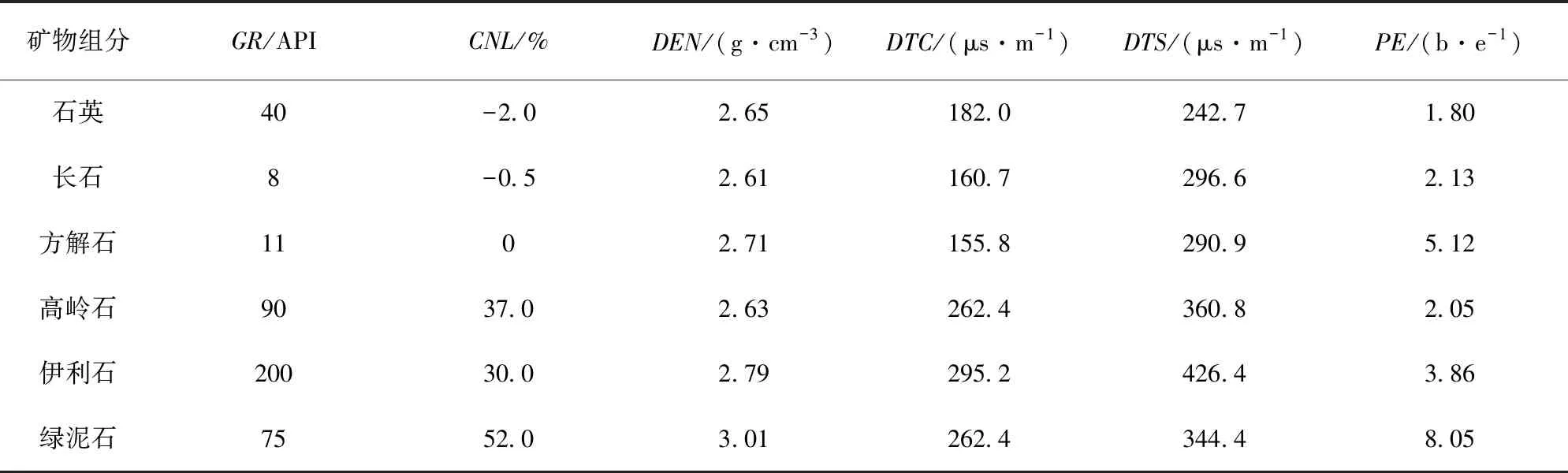
表1 研究区组分测井响应值参数表

2.4 处理结果

根据建立的模型及确定的参数，对研究区XX井进行了处理(图1)。图中第六道为最优化方法处理的剖面，第7～12道分别为最优化方法处理的石英、长石、方解石、伊利石、高岭石、绿泥石的含量，在1 790～1 805 m对岩心资料进行了X衍射实验。从处理的结果看，最优化方法计算的矿物组分含量与X衍射实验分析的结果基本吻合。

2.4.1 孔隙度

根据研究区储层生产情况，储层流体组分以水、气为主，并建立物理模型，根据最优化方法计算孔隙中流体组分水和气的相对含量，两种组分相对含量之和即为储层孔隙度。

φ=xw+xgas

(6)

式中，φ表示孔隙度，小数；xw表示水的相对含量，小数；xgas表示气的相对含量，小数。

从XX井计算的结果看(图1第13道)，最优化方法计算的孔隙度与岩心分析结果基本一致。

2.4.2 脆性指数

前人对脆性指数开展了大量研究，建立了根据矿物含量计算脆性指数的方法[11]，以用脆性矿物含量(主要包括石英、长石、方解石)占总矿物的比值建立了脆性指数的计算公式：

(7)

式中：BRIT表示脆性指数，无量纲；V代表不同矿物组分的含量，小数；

该方法对于脆性矿物整体含量不同的储层具有一定的指导意义，但对于非常规储层而言，在塑性矿物含量相似的情况下，主要为石英、长石、方解石三种脆性矿物含量的不同。这三种脆性矿物具有不同的断裂韧度，即分别在不同的压力下破裂。因此，廖东良、袁俊亮等[12-13]等根据不同矿物的断裂韧度对脆性指数的计算方法进行了改进。

(8)

(9)

KC为地层的综合断裂韧度，MPa·m1/2；KCi为第i种矿物的断裂韧度，MPa·m1/2；Wi为第i种矿物的体积分数。KCmax和KCmin分别为地层中断裂韧度的最大值和最小值，MPa·m1/2。根据国际岩石力学协会(ISRM)提供的不同矿物的断裂韧度可知：石英的断裂韧度为0.24 MPa·m1/2，长石的断裂韧度为0.85 MPa·m1/2，方解石的断裂韧度为0.79 MPa·m1/2，黏土矿物的断裂韧度为2.19 MPa·m1/2。该公式考虑了不同脆性矿物之间断裂韧度的差异，用断裂韧度作为矿物含量的加权系数来评价地层脆性指数可弥补公式(7)的缺陷，可以准确评价致密砂岩的脆性。

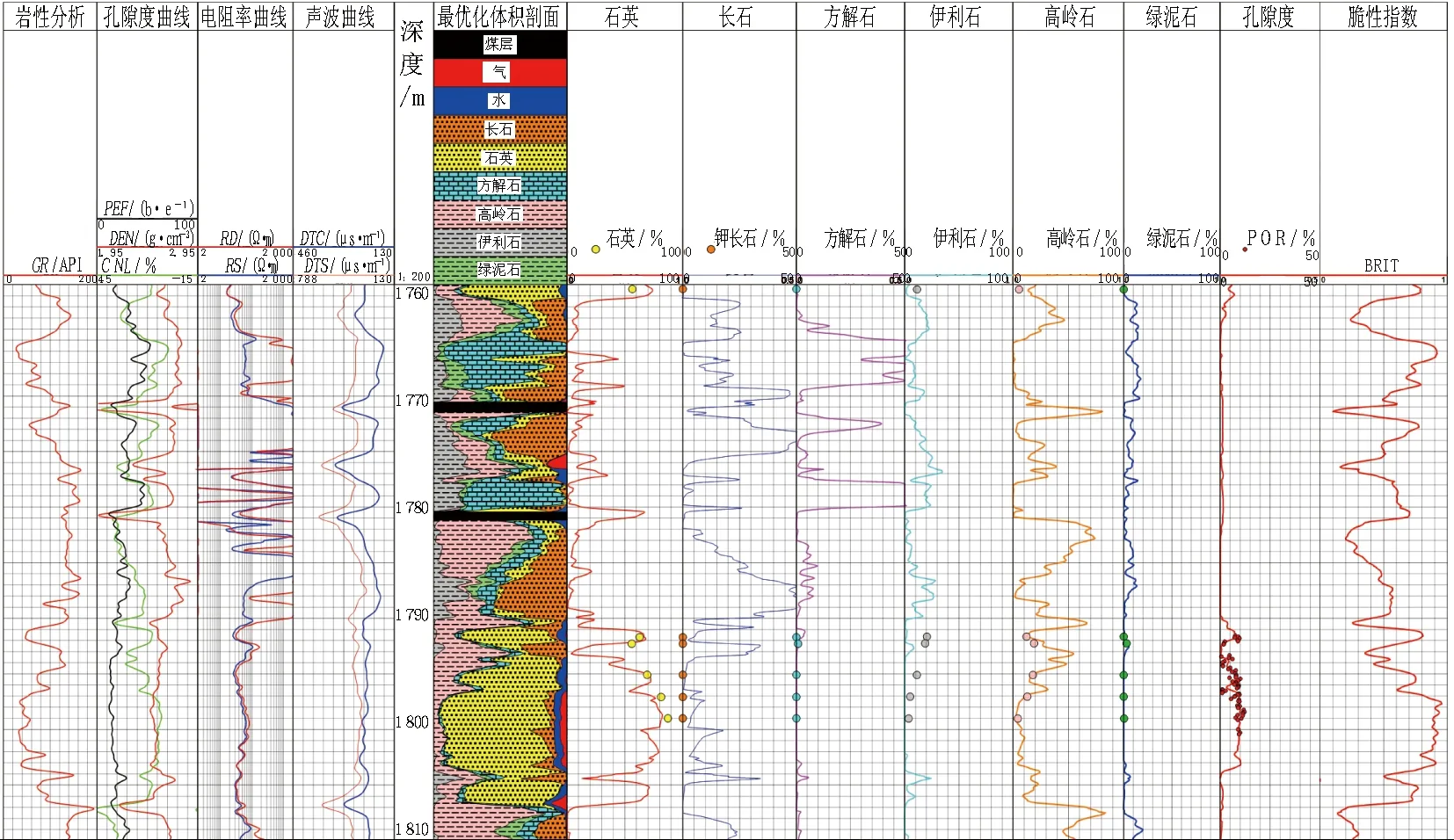
图1 XX井致密砂岩储层最优化方法处理结果

3 方法应用

根据最优化方法处理得到的孔隙度及脆性参数，对研究区致密砂岩储层后期压裂开发提供指导并进行产能预测。

3.1 压裂前层位优选

研究区石炭系本溪组—二叠系石千峰组具有多套含气显示砂体，在这些砂体中产气量变化大，从日产气几千方到几万方均有分布。在进行压裂之前需要对这些砂体进行优选，择优进行压裂开发。与常规储层相同，控制致密砂岩储层产能的主要因素中，储层孔隙度是其中之一。不同的是，致密砂岩储层脆性矿物含量(即脆性指数)对产能具有明显的控制作用，在孔隙度相似的情况下，地层越脆，压裂越容易产生微裂缝，产气量越高。

X井石盒子组A、B两套地层(图2、图3)，厚度、物性、含气性都相似，但是处理的矿物组分A层以石英为主，B层长石含量明显增多，通过计算，A层脆性指数大于B层。后期通过压裂测试，A层产气量较高，返排率75.15%，B层产气量较低，返排率45.13%，说明A层脆性好，压裂后缝网较好，使得储层连通性较好，所以压裂后产能较高，B层脆性较差，压裂后缝网较差，储层连通性差，所以压裂后产能较低。

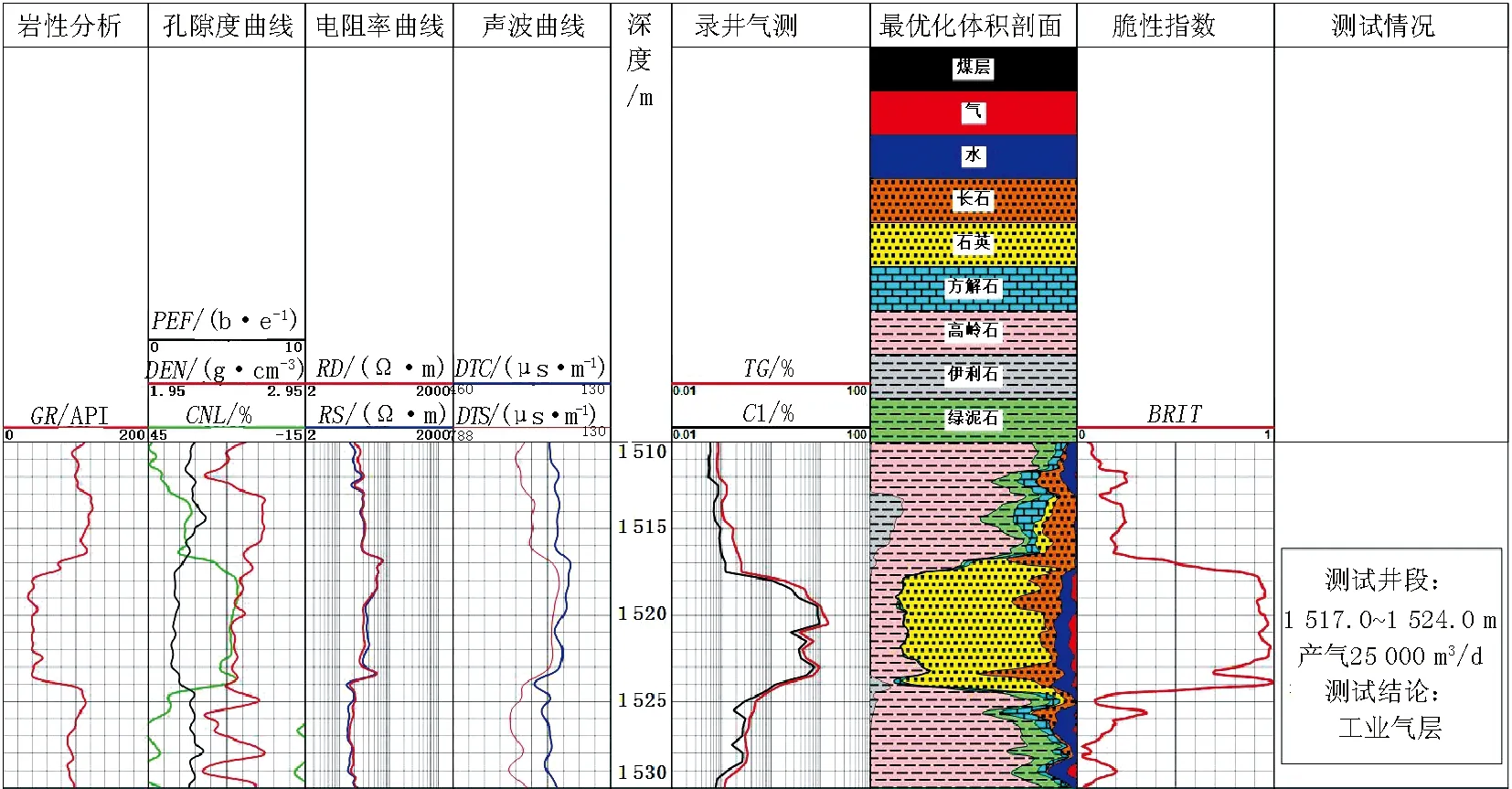
图2 X井A层处理成果

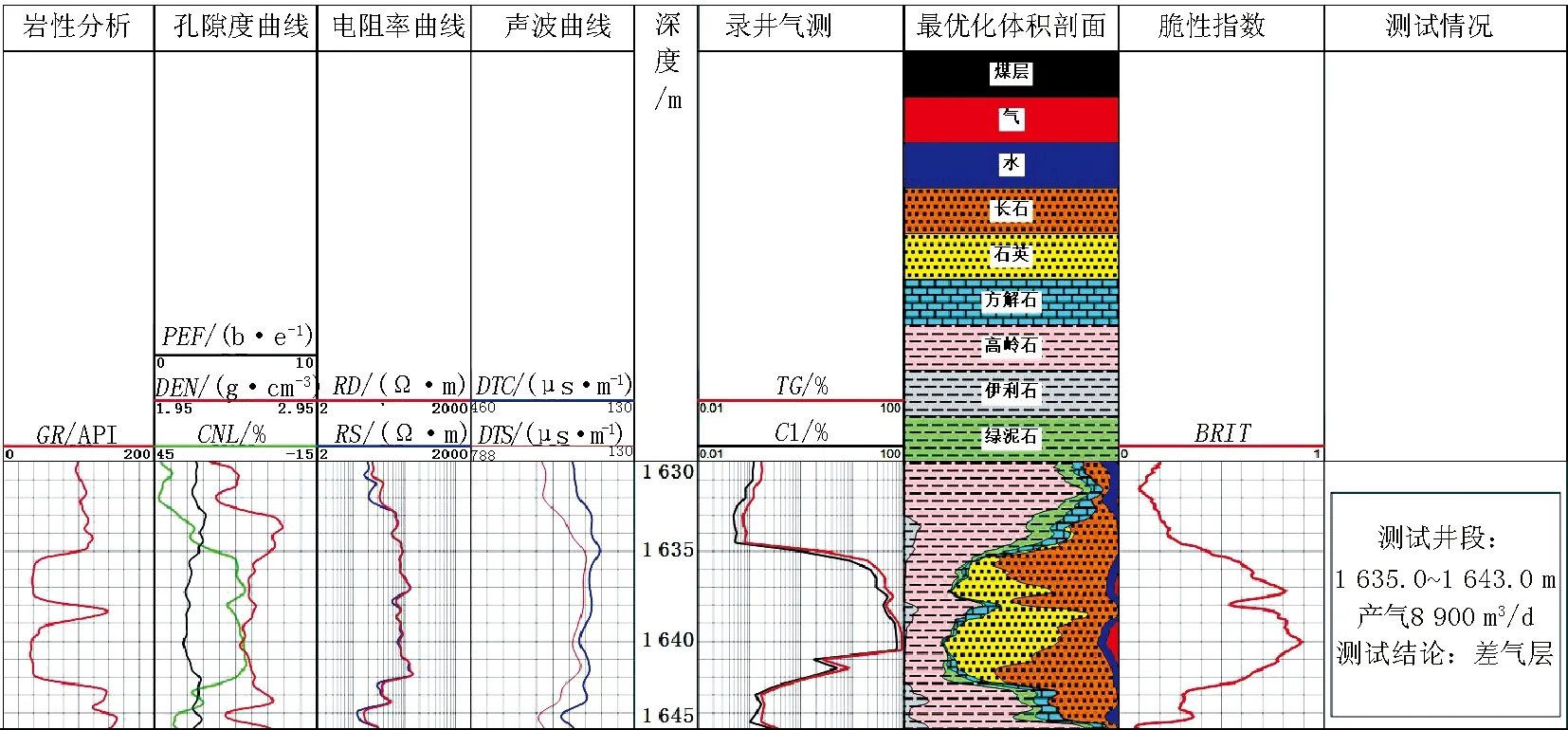
图3 X井B层处理成果

因此，根据脆性指数可以对压裂改造进行指导，进一步优选压裂层位，脆性好表示更利于造缝，产生缝网，获得高产的可能性越大。

3.2 压裂后产能预测

产能预测对致密砂岩也具有重要意义，可以有效缩减低产能层位的测试，节约大量测试成本。储层孔隙度对产能起着至关重要的作用，储层孔隙度越大，所含流体越多，因此高孔隙度储层的产能较高，中、低孔隙度储层的产能较低[14]。从孔隙度与单位厚度产气量拟合的关系上看(图4)，孔隙度大于8.5%的情况下，产能与孔隙度具有明显的正相关性，但孔隙度小于8.5%的情况下，产能与物性相关性不明显。由于致密气储层经过了压裂改造，产能与脆性指数也密切相关，因此建立产能预测模型时使用体现储层物性的孔隙度参数与体现储层改造能力的脆性指数，将物性、脆性综合在一起，使用最优化方法计算的孔隙度及脆性指数构建Z=Φ×BRIT这样一个综合评价指数，考察其与实际测试产能的关系(图5)。

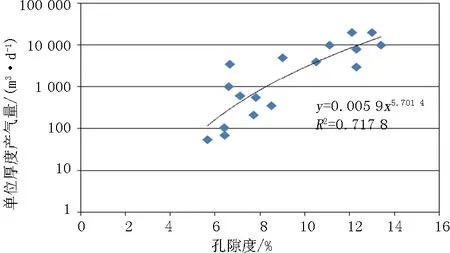
图4 孔隙度与产能相关性

根据拟合的关系，孔隙度小于8.5%的储层，物性与脆性综合评价指数与产能的相关性有明显的提高。因此，孔隙度大于8.5%的储层，物性是主控因素，使用孔隙度对产能进行预测，孔隙度小于8.5%的储层，物性与脆性结合进行产能预测效果更好。

根据以上方法，对Y井1 514.5～1 519.5 m使用最优化方法进行了处理(图6)，处理结果显示该套储层孔隙度8.3%左右，脆性指数0.86，使用孔隙度与脆性指数结合的综合评价指数对该套层进行了产能预测，预测产气9 795 m3/d，实际测试产气10 880 m3/d，预测结果与实际测试结果基本一致。

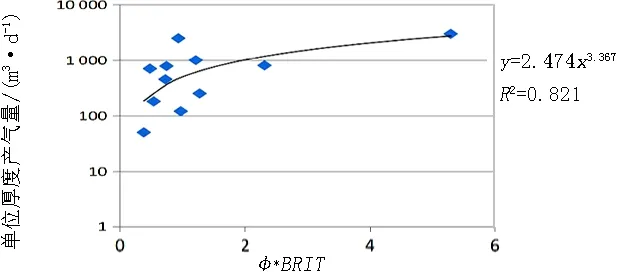
图5 孔隙度、脆性综合评价指数与产能相关性

图6 Y井最优化方法处理成果

4 结论

(1)针对致密砂岩储层矿物组分复杂的情况，根据最优化方法，对地层组分进行反演，建立了致密砂岩储层矿物组分分析方法，并根据求取的地层组分对测井曲线进行正演，结合最小二乘法原理，确定了区域响应参数；据此计算的矿物组分与X衍射实验结果吻合较好。

(2)根据最优化方法处理的结果，进而计算致密砂岩储层孔隙度以及脆性指数，计算的孔隙度与岩心分析结果可比性良好，有效指导了致密砂岩储层压裂改造及产能预测。

(3)最优化方法是一种基于常规测井资料的先进算法。综合利用所有反应储层特征的测井曲线可减小计算误差，在节省成本的同时为致密砂岩气勘探开发提供更多的参考依据。