Complementary Sliding Mode Speed Control with Saturation Function Boundary Layer Optimization

Yanwei Huang,Yuqing Xie and Wenchao Huang

(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116, China)

Abstract: A simple method is proposed to optimize the thickness parameter of the boundary layer of the saturation function in the Complementary Sliding Mode Control (CSMC). A pair of complementary sliding surfaces are constructed. And the Taylor series is used to estimate the steady-state error of CSMC system to optimize the parameter value for the boundary layer of the saturation function without artificial settings. This proposed CSMC strategy is applied to the speed regulation in permanent magnet synchronous motor with lump uncertainties. The experimental results show that the proposed CSMC strategy can obtain an optimal value for the boundary layer parameter, effectively suppressing the chattering, and keep an excellent system performance.

Keywords: CSMC; saturation function; boundary layer parameter; Taylor series; speed regulation

1 Introduction

Complementary Sliding Mode Control (CSMC) by designing a pair of mutually compensating sliding surfaces to modify the Sliding Mode Control (SMC), the phase trajectory converges to the equilibrium point along the intersection of the pair of sliding surfaces[1]. Compared with SMC, the steady-state error is reduced by a half[2-3]. However, the control law of CSMC is still using the sign function to ensure the system robustness, it is inevitable to result in the high frequency chattering. The use of the saturation function to replace the sign function is an effective method to weaken the chattering, and the control precision of the system is also be ensured[4-6]. However, the introduction of the saturation function adds a boundary layer parameter, which needs artificial settings[7]. The boundary layer parameter being too large will reduce the system steady state accuracy while being too small will aggravate the chattering[8]. Therefore, the boundary layer parameter setting is very important to ensure the performance of CSMC system[9]. A fuzzy function is used to design an approximate saturation function for SMC to regulate the speed of the induction motor. The optimization of the boundary layer parameter can be adjusted by the fuzzy rules according to the uncertainty of the system[10]. A modification of the SMC is proposed to improve the speed accuracy with the saturation function boundary layer parameter designed by fuzzy rules[11]. The nonlinear control design tool of MATLAB toolbox is used to optimize the boundary layer parameter of the saturation function of SMC, and the direct thrust control of linear motor is implemented[12]. In this method, the four parameters: switching gain, sliding mode surface coefficient, convergence law coefficient and boundary layer parameters, are optimized simultaneously. However, this algorithm has too high computational complexity.

In the CSMC system, the joint action saturation function and its switching gain suppresses the high frequency chattering[13-15]. Here, an optimization method of boundary layer parameter of the saturation function is proposed for CSMC strategy. Firstly, the complementary sliding surfaces are constructed by generalized and complementary sliding surfaces. Then the relationship between the boundary layer parameter and the switching gain is obtained by using the Taylor series to expand speed error. The boundary layer parameter optimization is solved for the saturation function. Moreover, the CSMC speed regulation is applied in the Permanent Magnet Synchronous Motor (PMSM) platform. Experiments show that the CSMC strategy with the optimization of the saturation function boundary layer does not require artificial settings and the optimal speed performance can be obtained at the same time.

2 CSMC Control System

2.1 PMSM Mathematical Model

Ignoring the effect of magnetic saturation, harmonic back electromotive force, hysteresis and eddy current loss, the mathematical model of the mechanical motion of the surface-type PMSM in thed-q-osynchronous rotating coordinate system is,

(1)

wherewis the rotor mechanical angular speed,Jis the moment inertia,Bis the viscous damping coefficient,Teis the motor electromagnetic torque,TLis the load torque,Kfis the electromagnetic torque coefficient,iqis theq-phase current in thed-q-ocoordinate system.

In consideration of the parameters perturbation, friction coefficient and other uncertain factors, Eq.(1) can be described as,

(2)

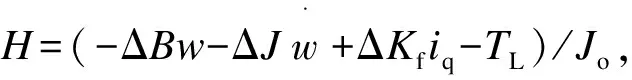
2.2 CSMC Speed Regulation

CSMC is applied to a speed control for PMSM, the definition of tracking erroreis,

e=w*-w

(3)

wherew*is the given rotor angular speed.

The generalized sliding surfaceSgis defined as[1],

(4)

where the coefficientλ>0.

Derivative of Eq.(4) is,

(5)

The complementary sliding surfaceScis,

(6)

The relationship between these two sliding surfaces is[1],

(7)

According to Eq.(2) of the system, the tracking error converges to the boundary layer within a finite time. The robust control law of CSMC is designed as,

(8)

whereieqis an equivalent control component,iris a robust control component.

(9)

(10)

whereρis a gain parameter,ρ>0,φis a saturation function boundary layer thickness parameter,φ> 0. The sat() is a saturation function as follows:

(11)

where sgn means the sign of the (Sg+Sc).

CSMC system stability proof.

Define the Lyapunov function is:

Derivative of Lyapunov function with Eq.(4), Eq.(7)-(8),

λe-λSc]=-λ(Sg+Sc)2-

H(Sg+Sc)+(Sg+Sc)·

|Sg+Sc||H|+(Sg+Sc)·

Whenρ≥D≥|H|, and |Sg+Sc|>φ,

That indicates the CSMC system satisfies a large scale asymptotic stability. Therefore, the sliding modulus |Sg+Sc| will converge to the boundary layer of the saturation function in a finite time, that means |Sg+Sc|≤φFrom Eq.(4) and Eq.(6), it has,

|Sg+Sc|=2|e|≤φ

(12)

Then the boundary of system tracking erroreis

(13)

Eq.(13) indicates that the steady-state error of the system will enter into the boundary layer thickness of the saturation function when the CSMC system enters the sliding mode. Apparently, the saturation function replaces the sign function, adding a boundary layer parameterφand theφvalue is usually artificially setting. Moreover,φhas an important influence on the CSMC system performance. If the parameterφvalue is too small, resulting in always |Sg+Sc|>φthe state trajectory cannot enter into the sliding mode and always stay at the boundary of the saturation function in turn, which result in the high frequency chattering. If the parameterφvalue is too large, the CSMC system keeps in the thickness range of the boundary layer, which will lead to the increase of the system steady state error and reduce the robustness. So the optimization of the parameterφis very necessary and important.

2.3 Parameter φ Optimization

In the CSMC system, the boundary layer parameterφof the saturation function is optimized. Derivative of Eq.(3) with Eq.(2) is,

In CSMC system,iqis the control variable with Eq.(9),

(14)

|Sg(t)+Sc(t)|=|2e(t)|≤φ

(15)

The sampling time of the control system is assumed to beT. Whent=t1, the sliding modulus has |Sg(t1)+Sc(t1)|=|2e(t1)| and the sliding modulus |Sg(t1+T)+Sc(t1+T)|=|2e(t1+T)| for the next sampling time. The Taylor series is used to expande(t1+T) to obtain,

(16)

Since |ψ(t)|≤ρ, so

(17)

|Sg(t1+T)+Sc(t1+T)|≤4ρT

(18)

Let the |Sg(t1+T)+Sc(t1+T)|=|2e(t1+T)|≤φand maximize the accuracy of the system. The thickness parameterφof the saturation function boundary layer is optimized as,

φ=4ρT

(19)

Eq.(19) shows that the saturation function boundary layerφin the CSMC method can be optimized to 4ρT. It means theφvalue is designed by the switching gainρand the sampling time of CSMC system, and does not need artificially setting.

3 PMSM Experiments

PMSM experimental servo platform is shown in Fig.1, composed of four components: PMSM+magnetic brake, DSP control subsystem, power inverter and computer. PMSM model: 60CB020C, rated voltage: AC220V, rated power: 200 W, rated current: 1.27 A, rated speed: 3 000 r/min, pole pairs:np=4, rated torque: 0.64 N·m, stator resistance:Ro=13 Ω, inductance:Lqo=Ldo=Lo= 0.032H, flux linkage coefficient:Ψf=0.119 Wb, moment of inertiaJo=0.000 15 kg·m2, sliding friction coefficientBo=0.000 1 N·m·s/rad. Magnetic brake model: CZ02, rated torque: 2 N·m, rated current: 0.5 A, slip power: 0.15 kW. Fig.2 is the structure of PMSM system by CSMC with the magnetic field oriented control strategy. The speed loop by using CSMC and current loop by PI controller are cascade control. The speed loop sampling frequency is 1 kHz. The control parameters are:λ=8,ρ=15, from the Eq. (19) to getφ=0.03.

Fig.1 PMSM experimental platform

Fig.2 Structure of CSMC system for PMSM

Fig.3 System speed error e with different φ values

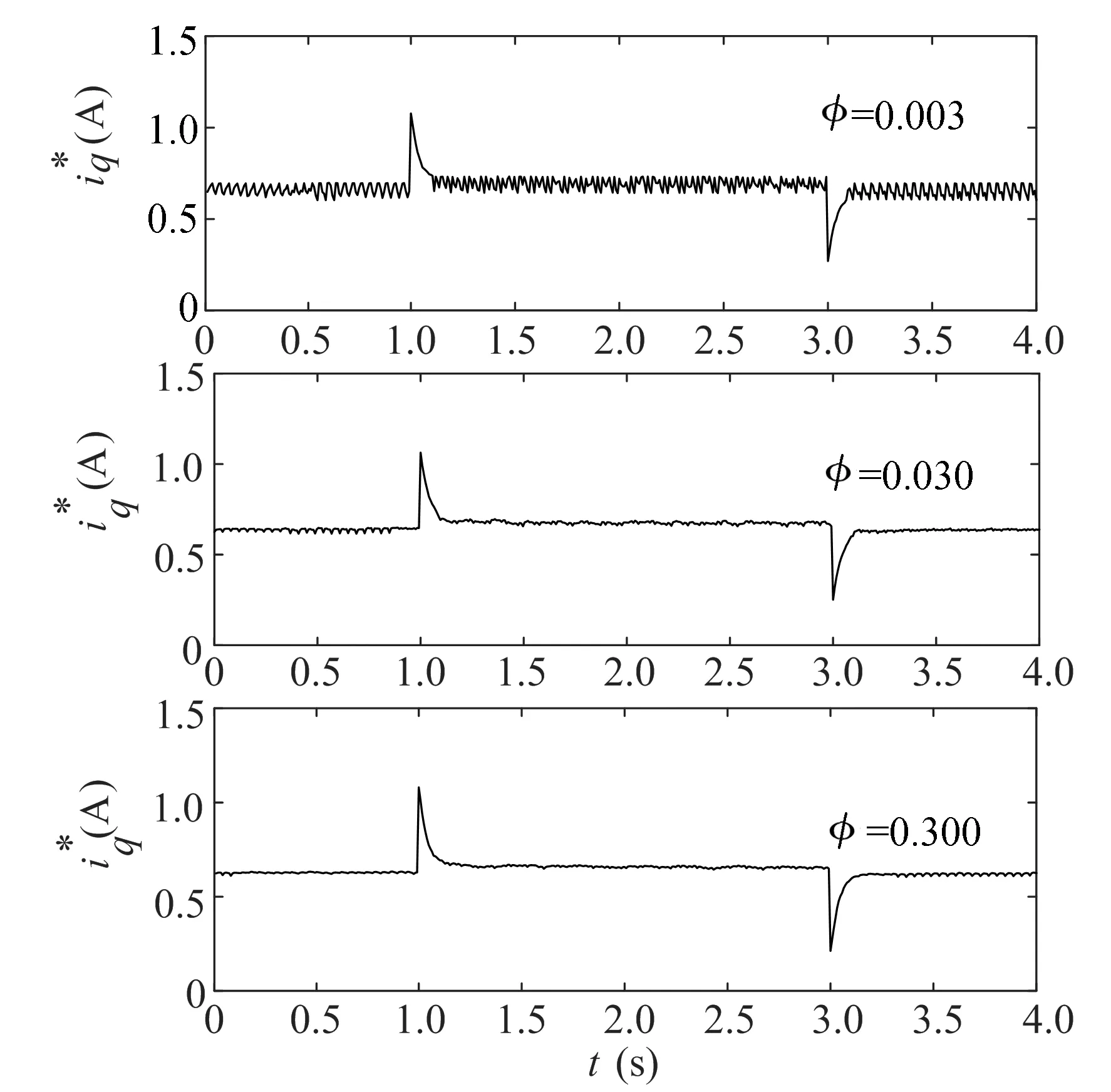
Fig.4 Control variable with different φ values

4 Conclusions

A parameter optimization method of the boundary layer of the saturation function is proposed to improve CSMC strategy. The boundary layer parameter is optimized as the expression of the switching gain and the sampling time, so as to avoid setting the boundary layer parameter artificially and improve the practicability of CSMC. The CSMC method is applied to the speed loop regulation in PMSM. The experimental results show that the boundary layer parameter optimization for the saturation function is effective for CSMC and can obtain a compromise between the high frequency chattering of the system and the system steady state error.