高频地波雷达海杂波抑制方法研究综述*

何康宁，尚 尚

高频地波雷达海杂波抑制方法研究综述*

何康宁，尚 尚

（江苏科技大学电子信息学院 镇江 212003）

高频地波雷达能够对海上目标实现超视距、全天候的探测，目前已经成为海上动目标检测的重要手段。但在复杂的海洋环境下，目标信号受海杂波影响较大，对海杂波进行有效抑制成为精确检测目标的关键。首先介绍高频地波雷达海杂波的形成机理，然后分别从对消类、小波变换类和子空间类三个方面对海杂波抑制方法进行综述。最后对现有方法存在的不足进行总结并展望未来研究的方向。通过综述为高频地波雷达海杂波抑制提供重要参考。

高频地波雷达；海杂波抑制；动目标检测；形成机理

引 言

高频地波雷达HFSWR（High Frequency Surface Wave Radar）采用垂直极化天线沿水平方向辐射高频电磁波，短波沿着海洋表面绕射传播不受地球曲率的影响，能够对海面目标实现超视距、全天候的探测，具有成本低、实时性好等特点[1]，成为探测海面和低空目标的重要手段。

高频地波雷达进行目标探测时，回波当中掺杂着大量的干扰信号，其中由海浪散射产生的回波称为海杂波。海杂波的一阶成分一般会等于或超过船只目标的检测阈值[2]，这成为有效探测海上低速目标的最大挑战[3]。国内外学者对海杂波的特性做了大量研究，相应的海杂波抑制算法层出不穷。文章在前人研究的基础上，首先介绍了高频地波雷达海杂波的形成机理，然后将已有的海杂波抑制方法分为对消类、小波变换类和子空间类三个主要类别，分别对每一类方法进行了综述，最后对目前海杂波抑制方法存在的不足进行总结，对未来的研究方向进行展望。

1 海杂波的形成机理

高频无线电磁波与正弦形海浪进行一阶作用，引起无线电波反射。当反射的无线电波长满足式（1）时，发生Bragg谐振散射，散射机理如下图1所示[4]。

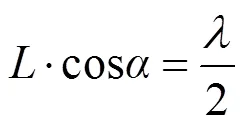
式中L为海浪波长，λ为高频无线电波长，α为无线电波的擦地角。当擦地角趋于零时，无线电波长是海浪波长两倍便可发生Bragg谐振，在多普勒谱中产生两个尖峰，称为一阶Bragg峰。

对于重力波浪，波长与特征速度B满足式（2），因此重力产生的多普勒频偏可以由式（3）给出[4]。

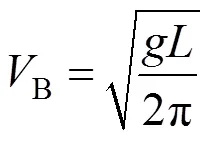
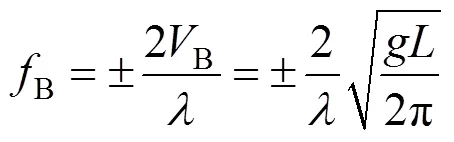
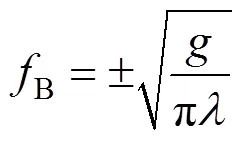
由于重力波相对雷达有正反两个运动方向，所以产生的多普勒频偏有正向和负向，在海杂波的多普勒谱中体现为正负两个尖峰。

高频雷达海杂波中一阶峰占主要分量，但是在一阶峰之外还有低几十分贝的连续谱存在，其中主要成分是二阶海杂波谱。Strivastava[5]等学者对二阶谱的形成机理已经做了详细研究，冀振元[6]等学者也阐述了二阶杂波形成的三种主要情况，同时从产生机理的角度提出了二阶海杂波的模拟方法。由于海杂波的二阶分量不是抑制的主要对象，对于它的形成机理不做过多说明。

2 海杂波抑制方法

2.1 基于模型的对消方法

基于统计特性的海杂波模型研究历时最长，发展最为成熟[7]。目前针对海杂波的幅度分布特性已经建立了很多较为成熟的模型，给海杂波抑制方法提供了重要理论基础。传统的海杂波幅度分布模型有对数正态分布、韦尔布分布、瑞利分布和K分布[8-11]等，四种典型模型由表1给出。在高分辨率和高海况条件下，海杂波幅度分布出现严重的拖尾现象，上述典型模型与实际海杂波数据偏差较大。为此，Middleton[12]等学者在经典模型上加以改进，在K分布的基础上发展形成KK分布、KA分布、WW分布[12, 13]等复合结构的幅度分布模型，拖尾区匹配效果得以改善。在基于模型的对消处理过程中，选择合适的模型对抑制效果至关重要。文献[14]在建立海杂波模型库的基础上，实现了对消模型的自适应选择。该方法首先根据雷达回波建立回波幅度分布直方图，再从模型库中选择与直方图最佳匹配的模型作为对消背景进行对消处理，实现海杂波的抑制。该方法要将众多模型与回波幅度分布直方图逐一比较以寻找最佳匹配，计算量较大，且适用程度取决于模型库中模型的完备性，工程运用中有较大局限性。

近年来，人们愈加认识到海杂波非线性建模的重要性。基于海杂波的多重分形特性[15]，任吉[16]等学者建立了高频雷达海杂波的时域分形模型并证明了其合理性，文献[17]通过空域和时域混沌特性实现了海杂波的重构。分形和混沌理论运用到海杂波建模当中，进一步弥补了线性建模精确性不足的缺点。另外，将神经网络运用到海杂波混沌模型的预测[18-21]也取得了一定的成果，利用神经网络预测得到的海杂波模型与雷达回波相减，可有效抑制海杂波提高信杂比。

目前，还没有普适性的海杂波模型。非线性理论在海杂波建模中的应用还不够成熟，理论需要进一步的简化。而神经网络的应用，前期需要大量的海杂波参数进行训练。因此，基于模型的对消方法，还需要从线性和非线性两个角度同时出发，建立更精确更具有普适性的模型。

表1 典型海杂波幅度分布模型

2.2 循环迭代对消方法

海杂波的主要分量可以近似看作正弦信号，在此基础上文献[22]提出在时域上减去正弦信号的方法来抑制海杂波，抑制效果取决于正弦信号参数估计的精度。最早的Root循环对消方案只考虑了正弦信号的幅度信息[23]，之后郭欣[24]等学者提出了基于FFT相位分析的频率估计法，在幅度信息的基础上还考虑了相位信息，进一步提高了正弦信号的估计精度。然而在短时间序列条件下，傅里叶谱分析难以提供足够高的多普勒分辨率。为此，文献[25]提出用扩展的Prony方法代替传统的FFT方法进行频率估计，文献[26]提出用傅里叶变换后最大的三根谱线进行插值来校正粗估计得到的频率，相对于传统的估计方法都有效提高了正弦信号参数估计的精度。

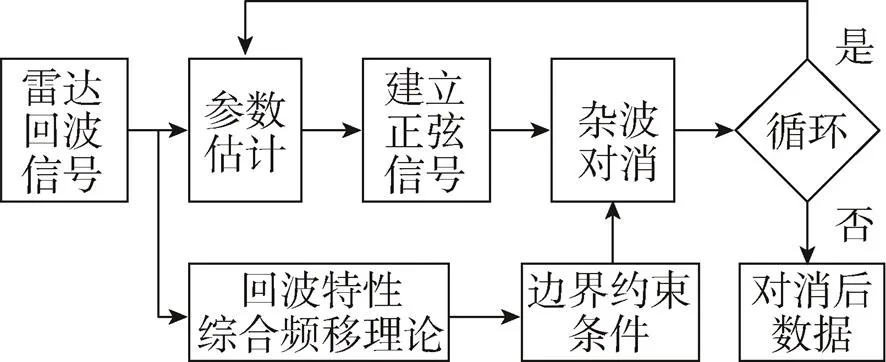
图2 带约束条件的海杂波对消流程

利用循环迭代对消方法抑制海杂波时，所估计的正弦信号是雷达回波当中强度最大的信号参量，一旦目标信号强度等于或超过海杂波信号强度，就会被误消而造成漏警。建立海杂波对消处理边界能在一定程度上避免这种情况发生。林志榕[26]等学者提出在一阶峰附近设置杂波界限，对消算法只在设置的界限内进行，一旦估计的频率超出界限就停止算法。王祎鸣[2]等学者将海杂波理论及海杂波的部分特性归结为边界约束条件，提出一种带约束条件的海杂波对消方法，将对消处理的范围约束在海杂波多普勒频率及其展宽范围之内，该对消算法的流程图由图2给出。

循环迭代对消方法在估计正弦信号参数时，精度不高会造成迭代次数的增多，剩余海杂波会在多普勒谱中扩散开来，影响海面和低空目标的检测。虽然边界约束条件的建立一定程度上减少了目标被误消的情况，但是当目标信号的多普勒频率落入海杂波中时，目前还没有较好的方法可以将两者分离以避免误消。另外，循环迭代对消的迭代次数一般都是由经验得出，没有严格的理论给出，选用不恰当的迭代次数仍会导致目标信号的误消或影响海杂波抑制的效率。

2.3 基于小波变换的抑制方法

基于小波变换的海杂波抑制方法，不依赖于杂波的统计特性，对复杂的海杂波具有良好的适应性。文献[27]研究表明，将小波运用到高频地波雷达目标检测当中，可以将信杂比提高至少20~30dB。小波变换分析用到的函数不具有唯一性，不同的小波函数运用到同一个工程有时结果相差很大。张静[28]等学者分别从阈值处理、边界处理和小波基的选取三个主要方面讨论了基于小波的算法选择，为基于小波变换的海杂波抑制方法提供了重要理论参考。

一般的实数小波变换不具备保留相位信息的能力，因此应用的局限性很大。文献[29]提出一种双数复数小波变换，该小波变换不仅能够保留相位信息，还能改善小波变换的平移敏感性，但运算量较大，硬件上实现困难。杨予昊等学者提出一种改进的可调小波变换TQWT[30]（Tunable Q-factor Wavelet Transform），这里的品质因子代表信号的振荡特性，表达式由式（5）给出

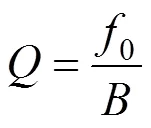
其中f0和B分别表示信号的中心频率和带宽。将雷达回波进行可调Q小波变换之后，在对应高品质因子的小波基函数上进行稀疏表示，由于目标信号的振荡特性高于海杂波信号，低品质因子的小波基函数被滤除，实现了小波域上的海杂波抑制，之后再用能量选择的方法提取表征目标的小波系数，通过反变换实现目标信号的重构，该算法的流程图如图3所示。

基于小波变换的海杂波抑制方法，在小波域内根据海杂波信号和目标信号的不同特性采取相应的阈值处理，以此实现海杂波的抑制。小波域内，高频部分表征海杂波方差，通过硬阈值处理将高频小波系数滤除就可以实现海杂波抑制[28]。又可以根据小波域内两类信号的相关性不同，设置小波系数的相关性阈值，实现小波域内的海杂波滤除[29]。该类方法不依赖海杂波模型和参数估计，可在小波域内实现海杂波信号与目标信号的分离并有效滤除杂波。

2.4 子空间类抑制方法

子空间类方法是根据杂波在子空间的聚集特性来实现海杂波的抑制。由于估计杂波子空间的方式不同，又可以分为特征值分解EVD（Eigen-value Decomposition）方法[31-33]和奇异值分解SVD（Singular Value Decomposition）方法[34-38]。

基于特征值分解的海杂波抑制方法，是将雷达回波的协方差矩阵进行特征值分解，根据特征值的大小将数据分配到不同的特征子空间，以此将雷达回波中的海杂波分离出去。但是当目标和海杂波的多普勒频率很接近时，特征子空间的超分辨谱分析会使目标谱产生分裂现象，造成虚警率上升。赵志国[32]等学者结合EVD方法引入了一种空域主瓣干扰抑制技术，较好的解决了目标谱分裂现象。目前在子空间类方法中，主要通过增加相干积累时间来提高频谱分辨率，而这又使得雷达回波的协方差矩阵维度增加，做特征值分解时产生较大计算量。为此，王道乾[33]等学者引入快速子空间法，该方法每次只估计协方差矩阵的最大特征值和特征向量并进行循环迭代对消。这就避免了对协方差矩阵直接进行特征值分解带来的计算量问题，与EVD方法相比，抑制效果相当但更易于工程实现。

基于奇异值分解的海杂波抑制方法，是将海杂波对应的奇异值置零以达到杂波抑制的效果。将雷达回波信号构造成Hankel矩阵，奇异值分解后得到

其中S是矩阵H的奇异值，U和V分别是对应奇异值的左右奇异矢量。传统的SVD抑制方法是将前两个较大的奇异值置零。但实际当中，目标信号的能量并不总小于海杂波信号能量，若单纯的将前几个较大的奇异值置零，很可能出现目标误消的情况。为此，鲁晓倩[36]等学者将右奇异矢量U做FFT后提取其中的频率信息，频率接近一阶峰就认为是海杂波频率，以此设置两个门限判决，将判决后的频率信息对应到奇异值，这样就可以有选择的对奇异值置零。王祎鸣[38]等学者提出了时频分析和奇异值分解联合处理的方法，在时域中估计雷达回波信号的瞬时频率，将其与奇异值分解得到的主奇异值相匹配，该算法的流程如图4所示。

该算法综合了两个处理域，实现海杂波奇异值的判决，使得奇异值置零更有针对性，提高了海杂波的抑制效果。

与对消类方法相似，子空间类方法只能在目标与海杂波多普勒频率距离较远的情况下实现海杂波抑制。当两者多普勒频率重叠时，无论是基于特征值分解还是基于奇异值分解的方法都不能将两者有效地分离开，往往会将落在海杂波多普勒频率内的目标信号误消，造成漏警。

3 结束语

高频地波雷达对海面和低空目标进行探测时，受海杂波的影响较大。文章对现有的抑制方法进行了综述，对不同方法的优缺点进行了分析和讨论。已有的方法虽然在一定程度上抑制了海杂波，但还有很多不足亟待完善。以下将对现有方法的不足进行总结并做合理展望：

①大多数海杂波抑制方法都会破坏目标信号特征的完整性，包括目标信号被误消和目标谱的分裂等。因此，需要深入研究海杂波特性，建立更多边界约束条件，使海杂波的消除更加精确可靠，减少对目标信号的影响。

②已有的方法大多只考虑目标信号与海杂波信号多普勒频率远离的情况，一旦目标多普勒频率落入海杂波中，往往会被误消而导致漏警。因此，针对两者多普勒频率重叠的情况，将来可以联系多个处理域，根据海杂波信号与目标信号在不同处理域当中的特性差异，实现两者的分离之后，再进行海杂波抑制。

③目前所建立的海杂波模型还远远不能描述不同海况下的海杂波。基于模型的抑制方法没有普适性，抑制效果存在很大的不稳定性。因此，需要从线性和非线性两个角度同时出发，建立更精确更具有普适性的海杂波模型。

[1] PONSFORD A M, SEVGI L, CHAN H C. An integrated maritime surveillance system based on high-frequency surface-wave radars, part 2: Operational status and system performance[J]. IEEE Antennas and Propagation Magazine, 2001, 43(5): 52–63.

[2] 王祎鸣, 毛兴鹏, 张杰, 等. 高频地波雷达海杂波的边界约束循环对消[J]. 海洋与湖沼, 2015, 46(2): 278–284. WANG Yiming, MAO Xingpeng, ZHANG Jie, et al. Boundary-constrained sea clutter circulation cancellation by high-frequency surface wave radar[J]. Oceanologia Et Limnologia Sinica, 2015, 46(2): 52–63.

[3] KHAN R, POWER D, WALSH J. Ocean clutter suppression for an HF ground wave radar[C]. IEEE Canadian Conference on Electrical & Computer Engineering, 1997.

[4] 冀振元, 孟宪德, 周和秘. 高频地波舰载超视距雷达海杂波特性研究[J]. 高技术通讯, 2001, 11(2): 40–44. JI Zhenyuan, MENG Xiande, ZHOU Hemi. Study on sea clutter characteristics of high frequency ground wave shipborne over-the-horizon radar[J]. High Technology Letters, 2001, 11(2): 40–44.

[5] SRIVASTAVA S, WALSH J. An analysis of the second-order doppler return from the ocean surface[J]. IEEE Journal of Oceanic Engineering, 1985, 10(4): 443–445.

[6] 冀振元, 孟宪德. 高频地波OTH雷达二阶海杂波分析及模拟[J]. 现代雷达, 2003, 25(4): 4–6. JI Zhenyuan, MENG Xiande. Analysis and emulation for second order sea clutter in high frequency ground wave OTH radar[J]. Modern Radar, 2003, 25(4): 4–6.

[7] CONTE E, MAIO A D, GALDI C. Statistical analysis of real clutter at different range resolutions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 903–918.

[8] 刘宁波, 孙艳丽, 丁昊, 等. 基于实测海杂波的典型幅度分布模型对比分析[J]. 计算机仿真, 2017, 34(5): 448–452. LIU Ningbo, SUN Yanli, DING Hao, et al. Comparative analysis of classical statistical models based on real sea clutter[J]. Computer Simulation, 2017, 34(5): 448–452.

[9] FAY F A. Weibull distribution applied to sea clutter[C]. IEEE Conference of Radar, 1977: 101–103.

[10] SANGSTON K J, GERLACH K R. Coherent detection of radar targets in a non-gaussian background[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 330–340.

[11] 张宝宝, 胡艳辉, 罗丰, 等. 相关K分布海杂波的建模与仿真[J]. 现代雷达, 2007, 29(4): 24–27. ZHANG Baobao, HU Yanhui, LUO Feng, et al. Modeling and simulation of correlated K-distribution radar sea clutter[J]. Modern Radar, 2007, 29(4): 24–27.

[12] MIDDLETON D. New physical-statistical methods and models for clutter and reverberation: the ka-distribution and related probability structures[J]. IEEE Journal of Oceanic Engineering, 1999, 24(3): 261–284.

[13] DONG Yunhan. Distribution of X-band high resolution and high gazing angle sea clutter[R]. Edinburgh South Australia: Defence Science and Technology Organisation,2006.

[14] 李家强, 姜庆刚, 陈金立, 等. 船舶导航雷达的海杂波自适应抑制算法[J]. 现代雷达, 2016, 38(2): 23–26. LI Jiaqiang, JIANG Qinggang, CHEN Jinli, et al. A sea clutter adaptive suppression algorithm for marine navigation radar[J]. Modern Radar, 2016, 38(2): 23–26.

[15] GAO J, YAO K. Multifractal features of sea clutter[C]. IEEE Radar Conference, Long Beach, CA,2002: 500–505.

[16] 任吉, 盛文. 一种新的高频雷达海杂波的分形模型[J]. 中国电子科学研究院学报, 2011, 6(5): 494–498. REN Ji, SHENG Wen. A new fractal model of radar sea clutter[J]. Journal of China Academy of Electronics and Information Technology, 2011, 6(5): 494–498.

[17] 李正周, 曹雷, 邵万兴, 等. 基于空时混沌分析的海面小弱目标检测[J]. 光学精密工程, 2018, 26(1): 193–199. LI Zhengzhou, CAO Lei, SHAO Wanxing, et al. Detection of small target in sea clutter based on spatio-temporal chaos analysis[J]. Optics and Precision Engineering, 2018, 26(1): 193–199.

[18] 王泉德, 文必洋. 高频地波雷达海杂波神经网络选择集成预测[J]. 系统工程与电子技术, 2009, 31(12): 2801–2805. WANG Quande, WEN Biyang. High frequency ground wave radar sea clutter predicting based on artificial neural network selection and ensembling[J]. Systems Engineering and Electronics, 2009, 31(12): 2801–2805.

[19] 何漫, 张亚璇, 解洪文, 等. 基于回声状态网络的OTHR海杂波抑制方法[J]. 雷达科学与技术, 2015, 13(4): 367–374. HE Man, ZHANG Yaxuan, XIE Hongwen, et al. Sea clutter suppression method of over-the-horizon radar based on echo state network[J]. Radar Science and Technology, 2015, 13(4): 367–374.

[20] 林三虎, 朱红, 赵亦工. 基于神经网络的海杂波模型[J]. 红外与毫米波学报, 2004, 23(1): 55–58. LIN Sanhu, ZHU Hong, ZHAO Yigong. Model for sea clutter based on neural network[J].Journal Infrared Millimeter and Waves, 2004, 23(1): 55–58.

[21] 谢红梅, 俞卞章. 基于神经网络预测器的混沌海杂波弱信号检测[J]. 现代雷达, 2004, 26(9): 50–52. XIE Hongmei, YU Bianzhang. Detecting weak signal in chaotic sea clutter using rbf neural network predictor[J]. Modern Radar, 2004, 26(9): 50–52.

[22] HAYKIN S. Radar clutter attractor: implications for physics, signal processing and control[J]. IEEE Proceedings-Radar, Sonar and Navigation, 1999, 146(4): 177–188.

[23] ROOT B T. HF-over-the-horizon radar ship detection with short dwells using clutter cancelation[J]. Radio Science, 1998, 33(4): 1095–1111.

[24] 郭欣, 倪晋麟, 刘国岁. 短时相干积累条件下天波超视距雷达的舰船检测[J]. 电子与信息学报, 2004, 26(4): 613–618. GUO Xing, NI Jinlin, LIU Guosui. The ship detection of sky wave over-the-horizon radar with short coherent integration time[J]. Journal of Electronics and Information Technology, 2004, 26(4): 613–618.

[25] 杨炼, 孙合敏, 潘新龙. 基于扩展Prony算法的海杂波循环对消法[J]. 现代雷达, 2011, 33(6): 53–57. YANG Lian, SUN Hemin, PAN Xinglong. Ocean clutter iteration cancellation based on extended prony algorithm[J]. Modern Radar, 2011, 33(6): 53–57.

[26] 林志榕, 胡进峰, 李会勇, 等. 一种改进的天波雷达海杂波循环对消算法[J]. 雷达科学与技术, 2014, 12(6): 597–603. LIN Zhirong, HU Jinfeng, LI Huiyong, et al. A modified ocean clutter cancellation algorithm in sky-wave radar[J]. Radar Science and Technology, 2014, 12(6): 597–603.

[27] JANGAL F, SAILLANT S, HELIER M. Wavelet contribution to remote sensing of the sea and target detection for a high-frequency surface wave radar[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(3): 552–556.

[28] 张静, 柳晓鸣, 索继东. 用于雷达信号杂波抑制的小波算法选择[J]. 中国航海, 2002, 2: 18–21. ZHANG Jing, LIU Xiaoming, SUO Jidong. The selection of wavelet algorithm of radar clutter processing[J]. Navigation of China, 2002, 2: 18–21.

[29] 任继, 程远, 刘溶. 双数复数小波变换在杂波抑制处理中的应用[J]. 现代防御技术, 2018, 46(3): 93–97. REN Ji, CHENG Yuan, LIU Rong. Dual-tree complex wavelet transform applications in clutter suppression[J]. Modern Defence Technology, 2018, 46(3): 93–97.

[30] 潘美艳, 杨予昊, 李大圣, 等. 一种基于能量选择的改进TQWT海杂波抑制算法[J].现代雷达, 2018, 40(10): 32–37. PAN Meiyan, YANG Yuhao, LI Dasheng, et al. Improved TQWT sea clutter suppression algorithm based on energy selection[J]. Modern Radar, 2018, 40(10): 32–37.

[31] WANG G, XIA X G, ROOT B T, et al. Manoeuvring target detection in over-the-horizon radar using adaptive clutter rejection and adaptive chirplet transform[J]. IEEE Proceedings-Radar, Sonar and Navigation, 2003, 150(4): 292–298.

[32] 赵志国, 陈建文, 鲍拯. 一种改进的OTHR自适应海杂波抑制方法[J]. 系统工程与电子技术, 2012, 34(5): 909–914. ZHAO Zhiguo, CHEN Jianwen, BAO Zheng. Modified adaptive ocean clutter suppression approach in OTHR[J]. Systems Engineering and Electronics, 2012, 34(5): 909–914.

[33] 刘定智, 王道乾. 基于循环子空间投影的杂波快速抑制方法[J]. 电视技术, 2018, 42(6): 58–63. LIU Dingzhi, WANG Daoqian. A fast clutter suppression method based on cyclic subspace projection[J]. Video Engineering, 2018, 42(6): 58–63.

[34] POON M W Y, KHAN R H, LENGOC S. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar[J]. IEEE Transactions On Signal Processing, 1993, 41(3): 1421–1425.

[35] LU K, LIU X, LIU Y. Ionospheric decontamination and sea clutter suppression for HF skywave radars[J]. IEEE Journal of Oceanic Engineering, 2005, 30(2): 455–462.

[36] 鲁晓倩, 孙荣. 修正Hankel矩阵SVD用于多模环境杂波对消研究[J]. 现代雷达, 2012, 34(3): 26–29. LU Xiaoqian, SUN Rong. A study on clutter cancellation method based on modified hankel matrix singular value decomposition[J]. Modern Radar, 2012, 34(3): 26–29.

[37] 薄超, 顾红, 苏卫民. 基于高阶奇异值分解的OTHR海杂波抑制算法[J]. 系统工程与电子技术, 2014, 36(5): 872–878. BO Chao, GU Hong, SU Weimin. OTHR sea clutter suppression algorithm based on high order sigular value decomposition[J]. Systems Engineering and Electronics, 2014, 36(5): 872–878.

[38] 王祎鸣, 张杰, 纪永刚, 等. 高频地波雷达海杂波抑制的时频-矩阵联合法[J].中国海洋大学学报, 2015, 45(3): 122–127. WANG Yiming, ZHANG Jie, JI Yonggang, et al. Joint time-frequency and matrix decomposition method on sea clutter suppression in HFSWR[J]. Periodical of Ocean University of China, 2015, 45(3): 122–127.

Review on sea clutter suppression methods of high frequency surface wave radar

HE Kangning, SHANG Shang

（School of Electronic and Information, Jiangsu University of Science and Technology, Zhenjiang, 212003, China）

High frequency ground wave radar has the ability to detect marine targets beyond visual range and all weather. At present, it has become an important means of moving target detection at sea. However, in the complex Marine environment, the target signal is greatly affected by sea clutter, and the effective suppression of sea clutter becomes the key to the accurate detection of targets. First, the formation mechanism of sea clutter of high frequency ground wave radar is introduced, and then summarizes the sea clutter suppression methods from three aspects: cancellation, wavelet transform and subspace. Finally, the shortcomings of the existing methods are summarized and the future research directions are prospected.This paper provides an important reference for sea clutter suppression of high frequency ground wave radar.

High frequency surface wave radar; Sea clutter suppression; Moving target detection; Formation mechanism

TN957.54

A

CN11-1780(2019)04-0010-07

何康宁 1996年生，硕士研究生，主要研究方向为高频地波雷达信号处理和海杂波抑制。

尚 尚 1982年生，讲师，硕士生导师，主要研究方向为高频地波雷达信号处理和电离层杂波抑制。

Email:ycyk704@163.com TEL:010-68382327 010-68382557

国家自然科学基金项目（61801196）；江苏省高校自然科学研究面上资助项目（17KJB510014）；江苏省研究生科研与实践创新计划资助项目（KYCX19_1692）。

2019-02-28

2019-07-20