一种求解稀疏重构问题的加速分割Bregman迭代算法
2019-11-04长江大学信息与数学学院湖北荆州434023
(长江大学信息与数学学院,湖北 荆州 434023)
稀疏重构模型在图像处理、机器学习、统计学中有着广泛的应用,其研究的主要内容为寻找欠定线性方程组Ax=y的稀疏解x[1]。其模型描述如下:
(1)
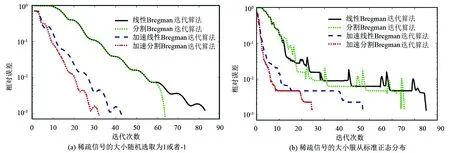
式中:A∈Rm×n;y∈Rm;x∈Rn且m 分割Bregman迭代算法是Osher等在研究图像去噪时提出的一种高效的迭代方法[2],该算法只需要利用目标函数的一阶导数信息,适用于大规模计算,被广泛的应用于图像去噪、图像去模糊等图像领域[3,4]。但这类方法仅具有线性收敛速率,在实际应用中求解速度较慢,这也就成为制约迭代算法应用的瓶颈。 Bregman迭代算法求解问题(1)的主要步骤如下:通过引入一个辅助变量z=x,将式(1)转化为: s.tz=x (2) 将其进一步化为非约束优化问题: (3) 式中:μ>0,且为一个常数。 (4) 可以直接利用文献[3]和[4]中给出的Bregman迭代算法来求解问题(4),算法主要步骤如下: (5) 式(5)中的第1个最小化问题可以分别对2个子问题xk+1和zk+1进行优化,即: (6) 对子问题xk+1的求解可采用多种方法。当问题规模不大时,对式(6)第1个式子的x进行求导并令导数等于0,可得: (λATA+μI)x=λATy+μ(zk-bk) (7) 此时可以直接得到x精确的解析解: xk+1=(λATA+μI)-1(λATy+μ(zk-bk)) (8) 式(8)中涉及到求逆运算,计算复杂度较高。 当问题规模较大时,矩阵求逆将耗费大量时间。此时可以采用Gauss-seidel法、傅里叶变换及共轭梯度法等得到式(6)的迭代解[4,12~15]。笔者采用梯度下降法得到x的近似解,x可以通过如下迭代得到: xk+1=xk-τ▽J(xk) 式中:▽J(xk)=λAT(Axk-y)-μ(zk-xk-bk)是目标函数在xk处的梯度。 子问题zk+1是一个稍微复杂的组合性问题,可直接利用收缩算子(软阈值)法[16]得到最优解,其表达式如下: (9) 式中: (10) 式(6)第2个式子是直接对b进行更新,将Nesterov加速梯度机制应用到b的更新上,得到新的b的迭代过程如下: (11) 综合式(7)~(11),加速分割Bregman迭代算法步骤如下: 输入:A,y; 当“不满足收敛性条件”,重复执行: ①根据式(7)或式(8)更新x; ②根据式(9)更新z; ⑥k=k+1; ⑦输出x。 将提出的加速分割Bregman迭代算法利用Matlab编程实现,并分别在无噪声和有噪声条件下验证算法的有效性。为更好地展现加速分割Bregman迭代算法的加速性能,还将该算法与未加速的分割Bregman迭代算法和线性Bregman迭代算法进行比较,同时也与目前已有的加速算法——加速线性Bregman迭代算法[8]进行比较。试验中,模型的各个参数选择如下:稀疏信号x的长度n=1000,其稀疏度(非零元的个数)k=100,稀疏元的位置随机均匀选取,稀疏元的大小分2种情况选取:①随机选取为1或者-1;②服从标准正态分布。观测矩阵A由如下方式产生:首先生成一个500×1000的随机矩阵,然后将矩阵的每一列规范化,使矩阵的每一列的范数为1。 观测信号y由y=Ax+n得到,其中n为服从标准正态分布N(0,σ2)的高斯白噪声,试验中取σ=0.1。 图1 算法重构性能比较 图1展示了当稀疏信号的大小随机选取为1或者-1以及服从标准正态分布时4种算法的重构性能。从图1(a)可以看出,线性Bregman迭代算法和分割Bregman迭代算法大约需要70次以上的迭代才能使得重构的相对误差达到指定精度;加速线性Bregman迭代算法所需的迭代次数大约在40次左右,加速分割Bregman迭代算法所需的迭代次数大约在30次左右,经过加速后算法的迭代次数约是不加速算法的一半,加速效果明显。加速分割Bregman迭代算法只需要30次左右的迭代即可达到所需精度,是所有算法中所需的迭代次数最少的。从图1(b)可以看出,此时各个算法所需的迭代次数较第1种情况均有较大的上升,但总体趋势并没有较大变化,加速分割Bregman迭代算法只需要120次左右的迭代,远低于其他3种算法。
1 算法步骤
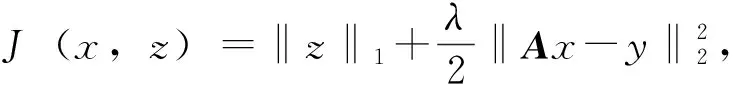
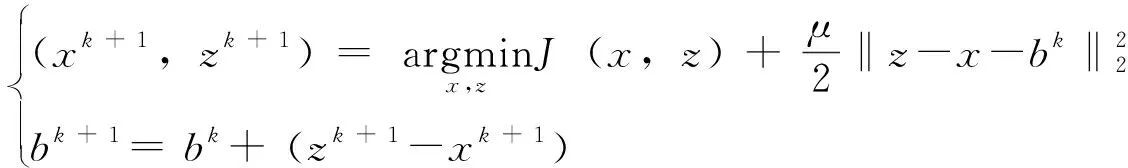
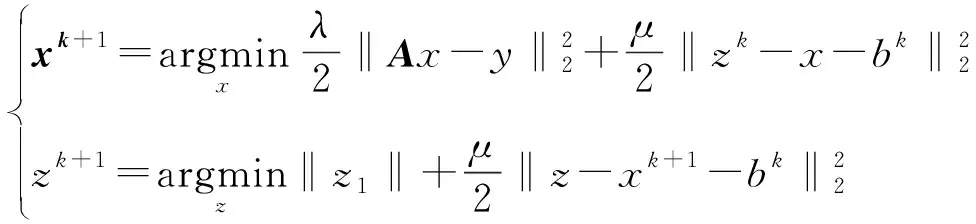
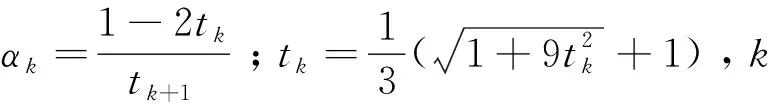
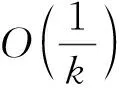
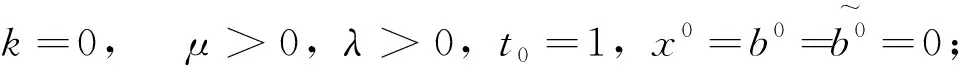
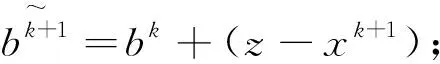
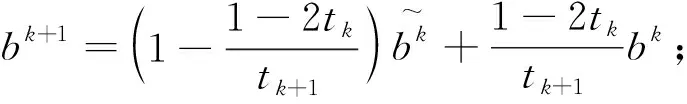
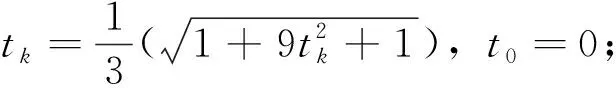
2 仿真试验
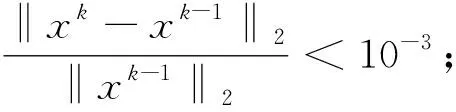
3 结语