一种基于健康度的多目标粒子群算法
2019-11-04长江大学信息与数学学院湖北荆州434023
(长江大学信息与数学学院,湖北 荆州 434023)
科学研究和现实工程设计中存在许多涉及多个数值目标的最优化问题,即多目标优化问题(multi-objective optimization problem,MOP)。通常情况下,多目标优化问题考虑的各个子目标互不相容,每个目标的物理意义和单位均不一致。一个解在满足某个目标的同时必须以牺牲其他目标为代价,所以多目标问题的解不是唯一的,而是存在一组既能满足全部约束条件同时又可使各个目标函数尽可能的达到最优的Pareto最优解集[1]。求解多目标优化问题的方法主要分为2大类[2]:①将多目标优化问题作适当的处理,如将多目标优化问题转化为一个单目标优化问题的线性加权法、将多目标优化问题转化为一系列单目标优化问题的层次分析法等。这类方法思路较为简单,发展较为成熟,计算量小,能找到多目标优化问题的非支配解,但这些方法也存在一定的局限性,如在优化时要求决策者对问题域有足够的先验认识才能给出较理想的转化参数,不适用于求解Pareto前沿为非凸的问题。②直接求出非劣解,然后从中选择较好解,如非支配方法。
粒子群优化算法(particle swarm optimization,PSO)是由美国社会心理学家Kennedy 和电气工程师Eberhart于1995 年提出的一种群体智能算法,该算法源于对鸟群觅食行为的模拟。PSO算法具有易理解、易实现、收敛速度快、求解精度高等优点,在多目标问题上得到了广泛应用。自2004年Colleo等[3]提出多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO)以来,许多研究者针对MOPSO计算复杂度高、通用性低、收敛性不好等缺点提出了改进的多目标粒子群算法。2006年,Sierra和Colleo[4]对各种多目标粒子群算法进行了归纳总结,指出单目标PSO扩展为MOPSO的3个关键问题:如何找到无限逼近真实Pareto解集的非支配解集、如何选择全局最优粒子、如何维护Pareto前沿上解的多样性;文献[5]使用Pareto支配概念来确定粒子的飞行方向,并采用聚类技术将决策空间中的种群分为几个子种群,对每个子种群执行PSO且子种群之间有信息交换;文献[6]引入了适应度共享概念,根据外部档案中的每个解共享值大小采用轮盘赌方式为每个粒子从档案选择全局最优粒子;文献[7]引入了一种新的粒子群算法的领导者选择方案,提出了一种与基于散点搜索的局部搜索方法相结合的多目标粒子群算法;文献[8]介绍了一种改进的粒子群优化算法(NSPSO),通过使用非支配排序概念和2种无参数的小生境技术,更好地实现多目标优化;文献[9]提出了目标空间压缩和扩展策略,利用群体间的知识共享更新PSO,构建了多目标粒子群算法中的动态多群算法。
以上提到的多目标粒子群算法是粒子群算法应用于多目标问题的重要研究成果,但还存在着收敛速度慢的问题,且在粒子维数较高的情况下,很容易过早陷入局部最优(早熟)。为此,笔者提出了一种基于健康度[10]的多目标粒子群算法(HMOPSO)。
1 模型与基本概念
假设x∈Rn,f:Rn→Rm,g:Rn→Rq,则多目标规划问题可表述为:
(1)
式中:x=[x1,x2,…,xn]T为决策变量;f(x)表示目标函数;g(x)为不等式约束;S={x∈Rn|gi(x)≤0}表示问题(1)的可行域。
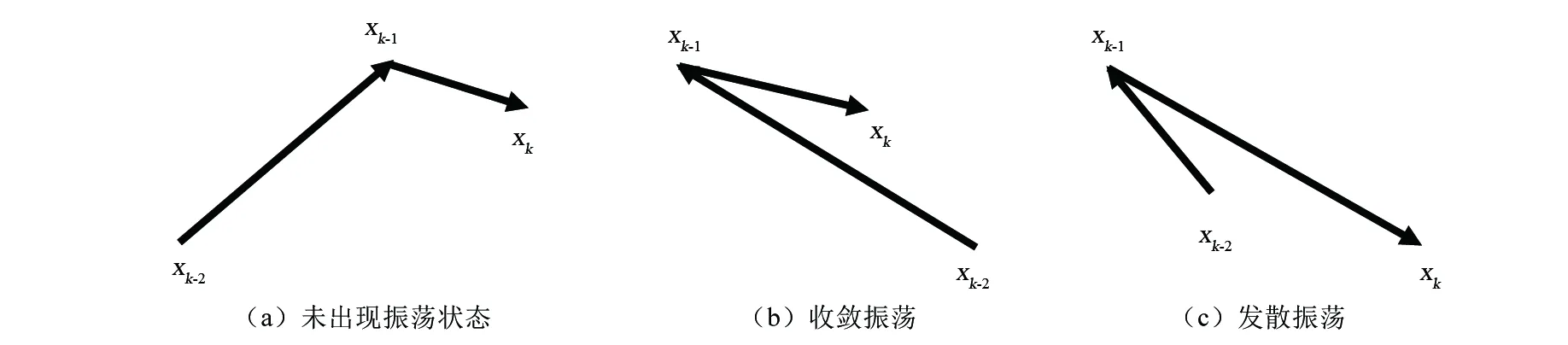
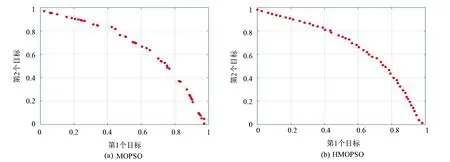
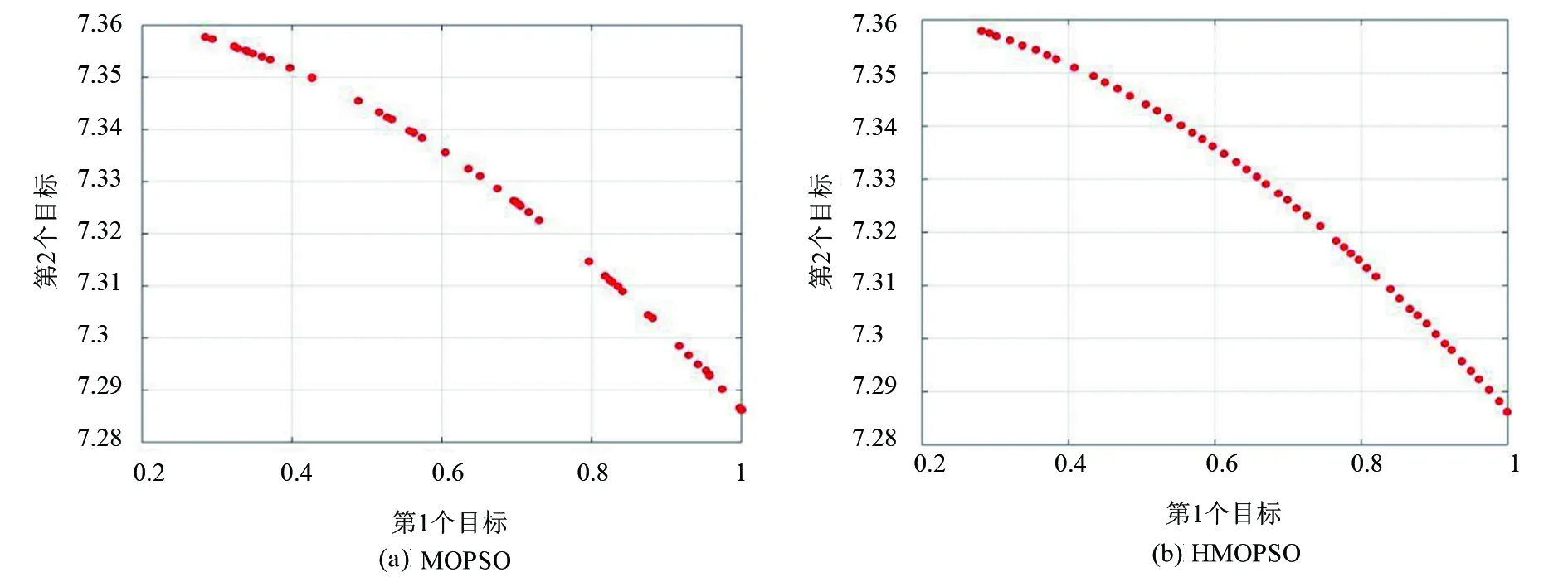
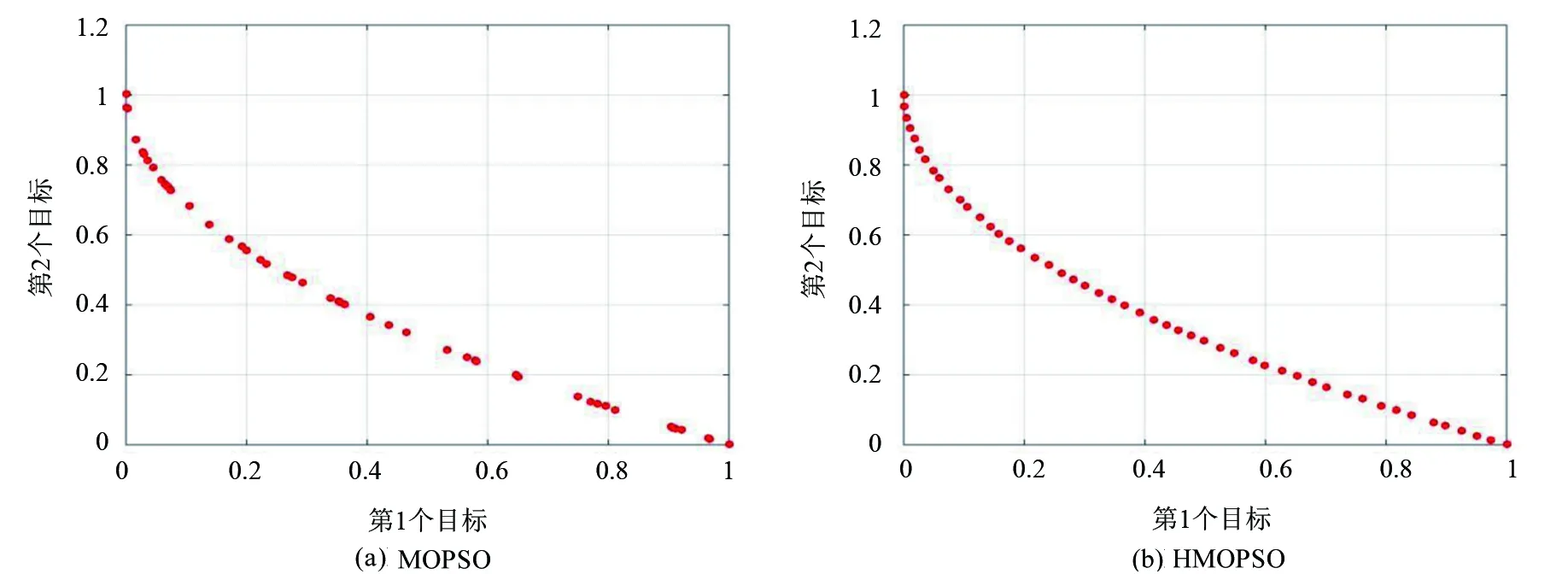
定义1(Pareto支配)对于任意2个可行解x和y,如果对∀i∈{1,2,…,m}满足fi(x)≤fi(y),且∃i∈{1,2,…,m}使fi(x) 定义2(Pareto最优解)如果x*是问题(1)的可行解, 并且不存在x∈S, 使得xx*, 则x*为问题(1)的一个Pareto最优解。 定义3(Pareto最优解集)所有问题(1)的Pareto最优解构成Pareto最优解集(Pareto-optimal set),记作: P*={x*∈S|∃x∈S,x*x} 定义4(Pareto前沿)对于给定问题(1)的所有Pareto最优解所对应的目标向量构成该多目标问题的Pareto前沿(Pareto Front),记作: PF*={f=(f1(x),f2(x),…,fm(x)|x∈P} 文献[10]提出了健康度的概念,用于衡量粒子在寻求最优解过程中的状态。在每一次迭代进程中,记录当前粒子的振荡数Nosc和停滞数Ns,越来越接近最优解的粒子健康度上升,反之下降。粒子健康度计算公式如下: H=100-min(wsNs+woscNosc,100) (2) 式中:ws和wosc分别是粒子的停滞次数和振荡次数的权值系数。测试时选择ws=0.8,wosc=3。 在粒子的运动过程中,如果粒子当前迭代与上一次迭代运行方向相异,则该粒子在此维度上出现振荡,粒子振荡状态的判定公式如下: (3) 式中:xi表示粒子在i状态下的位置。 在迭代过程中,若连续2代均满足式(3),则判定该粒子第1次出现振荡趋势。自第3代开始,只要满足式(3),则粒子振荡数加1,直至粒子被迫变异或者不满足式(3)时,Nosc重置为0。 粒子的运动轨迹可以表示为图1所示的3种状态,当粒子的运动轨迹表现为振荡状态,即粒子在某个维度上重复出现图1中(b)和(c)所示的2种状态时,通常会出现寻优停滞。粒子停滞数的确定如下: (i) 若当前粒子支配个体历史最优值时,粒子停滞数Ns记为0; (ii) 若个体历史最优值支配当前粒子时,粒子停滞数Ns加1; (iii) 若当前粒子与个体历史最优值不存在支配关系时,粒子停滞数Ns以0.5的概率加1。 图1 粒子运动轨迹示意图 在粒子维数较高时,粒子极易陷入早熟收敛,笔者引入的健康度体现了粒子向最优解的飞行状态,当粒子健康度下降至试验前设定的阈值时,则判定该粒子为异常粒子。对健康度过低的异常粒子,利用引导因子qi引导更新异常粒子的历史最优位置,改变粒子的运动轨迹,促使粒子跳出局部最优,在每一次迭代中减少异常粒子的数量,增强种群的整体健康度,保证种群的多样性。异常粒子位置更新为: xw=xw+rand(0,1)×(qi-xw) (4) 式中:qi为引导因子,即每次迭代的全局最优值。 整个搜索过程中,外部归档集的更新策略是获得一组好的Pareto最优解的关键。Deb等[11]使用了非支配排序方法解决多目标优化问题。Zitzler等[12]于1999年正式提出了具有精英保留机制的强度帕累托进化算法(SPEA)。Deb等[13]提出了更有效的非主导排序方法称为快速非支配排序。笔者利用给定最大容量的外部归档集来存储和更新每个迭代中的非支配解。最初,非支配解存储在空的外部归档集中。粒子X是否加入到当前外部归档集有3条规则:如果X被外部归档集中某个解支配,则X不加入;如果X支配外部归档集中某一个或多个解,则X加入外部归档集中并删除掉外部归档集中被X支配的解;如果X不支配外部归档集中任何解且外部归档集中没有解支配X,则X加入到外部归档集中。 当外部归档集中解的个数超出预先给定的范围时需要删除多余的部分。文献[13]通过计算每个粒子的拥挤距离删除拥挤距离小的粒子。针对m个目标的多目标问题,非支配解集为I,粒子拥挤度距离的计算方法步骤如下: 根据商务英语专业跨境电商方向人才培养目标和对行业企业的调研,在全面分析跨境电商岗位所需知识结构和岗位技能的基础上,我们提出基于职业素养的岗位基本能力、岗位核心能力和拓展能力构建跨境电商方向的课程体系。 Step1初始化距离,对每个I中的粒子i,令I[i]distance=0; Step2对目标j∈m,根据目标函数值对l个粒子进行升序排列(l=|I|为解集中粒子个数); Step3令I[1]distance=I[l]distance=∞,以保证边界点始终被选中; Step4第2个至第l-1个粒子的拥挤度计算公式如下: (5) 式中:cj(i)为第i个粒子在目标j的目标函数值。 在算法中,通常种群距离越小的粒子,分布度就越差,当非支配解集中粒子个数超过种群规模时,则需根据拥挤距离大小的排序,淘汰多余的粒子。传统的淘汰机制是直接淘汰拥挤距离较小的k个粒子,显然,这种方法较为粗糙,可能会导致个体的缺失,使得解的分布性较差。鉴于此,笔者采用动态的拥挤排序的方法来控制外部存档的规模[14],每计算一次拥挤距离,就删除掉拥挤距离最小的一个粒子,重复下去,直至淘汰所有多余的粒子。 对于PSO算法,粒子的速度和位置更新公式为: (6) 式中:pij(t)表示第i个粒子的历史最优位置;gj(t)表示全局最优位置;w为惯性权重;c1和c2为学习因子;r1和r2为[0,1]间随机数。HMOPSO的具体计算步骤如下: Step1初始化粒子群:设定种群规模N、外部归档集大小Ne、最大迭代次数M、随机产生粒子初始的位置Xi、初始速度Vi、个体极值pbest[i]、全局极值gbest。 Step2计算每个粒子的适应度函数值,并根据粒子适应度确定粒子间的支配关系,将非支配解放入外部归档集中。 Step3根据式(6)更新粒子的速度与位置,并重新计算适应度值。 Step4基于健康度更新个体最优粒子: (i) 计算粒子停滞数和振荡数; (ii) 更新粒子健康度; (iii) 若粒子健康度小于给定阈值H,执行变异操作,改变其局部最优位置,变异后,粒子健康度重新恢复到100。 Step5更新外部归档集。 Step6更新全局极值。 Step7判断是否满足终止条件,若满足,退出,否则返回Step 3。 为测试HMOPSO算法的效果,笔者对FON、ZDT6和ZDT1这3个不同维度的典型函数进行测试: s.t.-4≤xi≤4,i=1,2,3 ZDT6:minf1(x)=1-exp(-4x1)sin6(6πx1) s.t.0≤xi≤1,i=1,2,…,10 ZDT1:minf1(x1)=x1 s.t.0≤xi≤1,i=1,2,…,30 试验中给定MOPSO和HMOPSO的参数:学习因子c1=1,c2=2,惯性权重w=0.5,粒子群规模N=100,最大迭代次数M=400,最低健康度H=88。由MOPSO和HMOPSO分别所得3个测试函数的Pareto解绘制的Pareto前沿如图2、图3、图4所示。从图2~图4可以看出,MOPSO和HMOPSO均能得到有效的Pareto前沿, HMOPAO得到的Pareto前沿更加均匀,且更接近真实Pareto前沿。试验结果表明了HMOPSO能保证种群的多样性和Pareto前沿分布上的均匀性,对解决多目标问题具有重要的借鉴意义。 图2 测试函数FON的Pareto曲线 图3 测试函数ZDT6的Pareto曲线 图4 测试函数ZDT1的Pareto曲线 提出了一种基于健康度的多目标粒子群算法HMOPSO。该算法采用了健康度的概念来使粒子跳出局部最优,并在拥挤距离基础上,使用了动态拥挤排序的外部归档集维护策略。试验结果证明,该算法具有较强的全局搜索能力和获得好的Pareto最优解的能力。相比于MOPSO,HMOPSO的Pareto解集在多样性和分布均匀性上具有明显的优势。2 健康度
2.1 粒子的振荡数Nosc
2.2 粒子的停滞数Ns
2.3 异常粒子的变异
3 HMOPSO
3.1 外部归档集的更新策略
3.2 动态拥挤排序的外部归档集维护策略
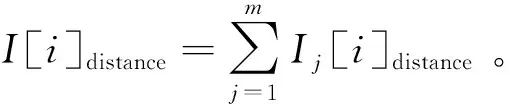
3.3 HMOPSO具体计算步骤
4 仿真试验
5 结语
